适用于提高T型三电平储能变流器功率响应特性的模型预测控制算法
2017-01-10刘建锋秦露露
刘建锋,秦露露
(上海电力学院电气工程学院,上海市 200082)
适用于提高T型三电平储能变流器功率响应特性的模型预测控制算法
刘建锋,秦露露
(上海电力学院电气工程学院,上海市 200082)
模型预测控制(model predictive control, MPC)已经广泛应用于电池储能系统。在传统中点钳位式(neutral point clamped,NPC)三电平储能变流器的每个开关周期内,其输出电压跳变不能超过直流母线电压的一半,该特点将严重影响变流器模型预测控制的功率响应特性。为此,提出一种基于T型三电平储能变流器的模型预测控制算法。在确保变流器输出有功功率、无功功率及中点电位偏差一定的前提下,采用遍历法寻求使变流器开关频率最低时的输出电压矢量,充分发挥T型三电平拓扑输出电压跳变不受限制的优势。采用几何分析法对比T型拓扑与NPC拓扑储能变流器的功率控制特性,分析结果表明,所提模型预测控制算法极大地提高了T型三电平储能变流器的功率控制特性。
储能;T型三电平变流器;NPC三电平变流器;功率控制;模型预测控制
0 引 言
电池储能是一种常用的分布式能量存储方式,具有能量密度高、技术成熟、环境适应性强等优势,应用前景广阔。通过引入电池储能系统,可有效缓解可再生能源发电的间歇性、波动性对电网带来的负面影响,实现“风光储一体”多能源互补[1-3],提高供电可靠性。因而近年来,电池储能系统(battery energy storage system,BESS)的研究受到了国内外学者的广泛关注[4]。能量转换系统(power conversion system,PCS)是BESS中负责能量双向变换的关键部件。传统的储能PCS采用两电平桥式变流器结构,结构简单易于实现,但受限于目前的功率半导体技术,此种结构的输出谐波较大,对滤波电感有较高要求,不利于功率密度和效率的提升[5]。因此,日本学者Nabae等人提出了一种基于二极管中点箝位(neutral point clamped,NPC)的三电平拓扑[6]。近年来随着绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)技术的进一步成熟,T型三电平拓扑作为一种改进的NPC三电平拓扑[7-8],在1 200 V以下领域已高度商业化。因而本文将此种拓扑引入到储能变流器领域,并对其功率控制算法进行研究。
目前PCS的功率控制多采用基于电网电压定向(voltage oriented control,VOC)的矢量控制方式[9],通过坐标变换将输出电流分解为有功和无功分量,实现有功和无功功率的解耦控制。电流的跟踪可通过比例积分(proportional integral,PI)控制、滞环控制和单周控制等方式实现,PI调节器能够保证良好的稳态跟踪精度,但PI控制的滞后制约功率响应速度;滞环控制和单周控制可提高响应速度,然而难以数字化实现限制了其应用。直接功率控制(direct power control,DPC)相较VOC控制,是一种对功率直接进行闭环控制的控制方式[10],根据功率偏差及电网电压通过离线查表的方式确定逆变器输出电压矢量,缺点是离线查表的实时性较差。虚拟同步发电机(virtual synchronous generator,VSG)控制采用有功调节并网频率、无功调节逆变器输出电压的控制方式[11],从而使得并网逆变器在外特性与内在机理上与同步发电机相似,该类控制方式可在多逆变器并联运行及其并、离网无缝切换中发挥巨大作用,但是,不适用于要求功率快速响应的场合。
模型预测控制(model predictive control,MPC)是一种应用于电力电子领域的新型控制算法,由于其具有动态响应快、控制目标灵活、易于处理多变量控制等优势,近年来已发展成为电力电子控制领域的一个重要研究分支[12]。针对电压源型逆变器输出有限个电压矢量的特点,文献[13]提出了一种应用于电压源型变流器的有限控制集模型预测控制(finite control set model predictive control,FCS-MPC)算法,以期望电流作为控制目标,根据变流器离散化模型,采用遍历法寻求使电流偏差最小的电压矢量输出。文献[14]针对逆变器并联系统的协调控制问题,将逆变器的MPC与下垂控制相结合,从而实现逆变器并联系统的无互连线模型预测控制。文献[15]将MPC应用于储能变流器,解决大功率储能系统因开关频率低、延迟高引起的系统不稳定问题。文献[16]提出了一种基于虚拟磁链MPC的新型脉冲宽度调制(pulse width modulation, PWM)算法,通过加权求和的方式将减小磁链偏差和降低开关频率多目标寻优转化为单一目标函数的寻优。文献[17]针对NPC三电平变流器有功功率、无功功率、中点电位等多目标控制要求,采用满意优化代替传统多目标控制中的权值函数,避免了整定复杂的权值系数并且获得更多控制自由度。然而,NPC三电平拓扑变流器每次开关动作输出电压跳变不能超过直流母线电压一半的固有特性,限制了其无法采用遍历法寻求最优电压矢量,使得基于NPC三电平拓扑的MPC难以获得最优控制效果。
针对NPC三电平拓扑变流器每次开关动作输出电压跳变不能超过直流母线电压一半的局限性,本文提出一种基于T型三电平储能变流器的模型功率预测控制算法。该算法在确保变流器输出有功功率、无功功率及中点电位偏差一定的前提下,采用遍历法寻求使开关频率最低的电压矢量输出,充分发挥T型三电平拓扑输出电压跳变不受限制的优势,从而增加MPC滚动优化的自由度,提高控制精度。采用几何分析法论证T型拓扑较NPC拓扑采用MPC具有优势的原因,最后通过仿真比较2种拓扑的控制效果,验证本文所提算法的优越性。
1 数学模型与换流过程
1.1 T型三电平储能变流器数学模型
T型三电平储能变流器系统结构如图1所示,直流侧为电池储能系统,交流侧通过滤波器与电网相连。图中LA,LB,LC为滤波电感值;RA,RB,RC为滤波器寄生电阻值;eA,eB,eC为电网各相电压;LP、LN分别为正、负直流母线;O为直流侧中性点;UP、UN为变流器正、负直流母线电压;Udc为直流母线总电压。
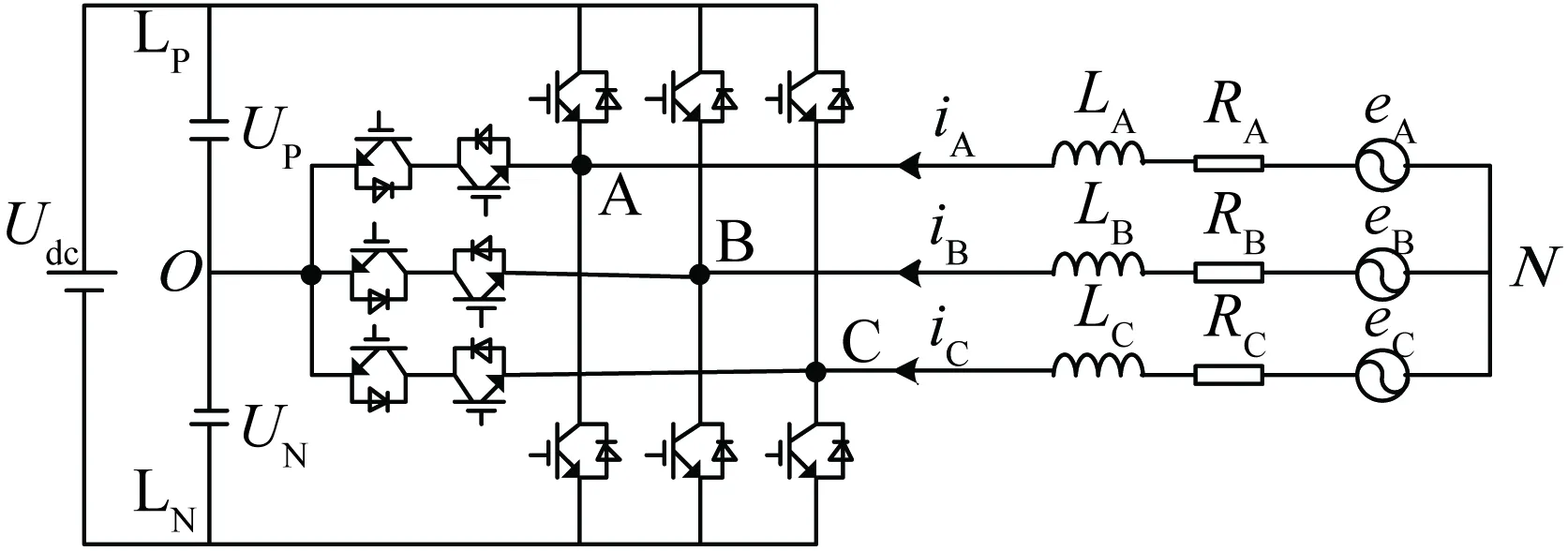
图1 T型三电平储能变流器系统结构
为便于分析首先定义逻辑开关函数SA、SB、SC∈{+1,0,-1}[17],分别表示变流器各桥臂对应开关状态,+1状态对应桥臂输出电压为Udc/2,0状态对应桥臂输出电压为0,-1状态对应桥臂输出电压为-Udc/2,其中参考电位为直流侧中性点O。根据基尔霍夫电压定律(KVL)建立T型三电平储能变流器三相回路方程:
(1)
式中;iA,iB,iC为储能变流器输入的三相电流;eA,eB,eC为三相电网电压;L为每相滤波电感;R为每相滤波电感的寄生电阻;uON为储能变流器直流侧中性点与电网中性点之间的电压偏差。
假设系统三相电网平衡(eA+eB+eC=0)可得其在两相静止αβ坐标系下的数学模型:
(2)
式中:iα、iβ表示三相变流器输入电流在αβ坐标下的α、β轴分量;uα、uβ表示三相变流器网侧输出电压在αβ坐标系下的α、β轴分量;eα、eβ表示三相电网电压在αβ坐标系下的α、β轴分量。
根据瞬时功率理论,电网向T型三电平储能变流器传递的有功功率P、无功功率Q可表示为
(3)
为得到功率P、Q的变化率,对式(3)求微分如下:
(4)
电网电压eα、eβ变化率可表示为
(5)
式中E为电网电压矢量幅值;ω表示电网角频率。
将式(2)、(5)代入式(4)并整理得:
(6)
采用牛顿一阶前向差分方法对式(6)离散化处理,采样周期为Ts,可得:
(7)
由于三电平拓扑的特殊性,中线上会存在电流流过,其上下电容会产生分压不均情况,造成中性点电压的偏移。T型三电平变流器与传统NPC三电平变流器都存在中性点电位偏移问题。如图1所示,O即为T型三电平储能变流器中性点,其电位由上、下电容电位共同决定。设中性点电位Uo=UP-UN,其中UP、UN分别是上、下电容电压,则中性点电位变化率可描述为
(8)
式中C为直流母线单个上电容或者下电容的容值,上、下电容容值相同。
由于系统三相对称则三相电流之和为0,对式(8)进一步化简并转化到两相静止坐标系下得到如下表达式:
(9)
式中Sα、Sβ分别为变流器各桥臂对应的开关状态在αβ坐标系下的α、β轴分量,同样采用牛顿一阶前向差分方法对式(9)离散化处理,采样周期为Ts,可得:
(10)
1.2 换流过程对比
对于传统NPC三电平变流器,桥臂每个开关管只能承受一半的直流母线电压。因此,每次开关动作其输出相电压不能产生超过Udc/2的电压跳变,否则会造成功率开关器件过电压损坏[17]。例如,当桥臂开关状态由+1跳变为-1时,使得上桥臂第2个开关管承受电压Udc而损坏[18]。相应地,每次开关动作27条空间电压矢量并非均可相互切换。图2给出了三电平变流器电压矢量跳变原理图,以当前开关状态+- 0为例,下一开关周期可选电压矢量共有11条,如图2带箭头虚线所示,分别为+-+、0-+、 0-0、+ 0 +、0 0 0、0--、+ 0 0、0 0 -、+ 0-、+--及+-0,电压矢量对应的点表示为空心点,其余16条空间电压矢量均因造成功率开关器件过电压而被排除。
T型三电平储能变流器桥臂的上或下开关管承受电压为直流母线电压Udc,该拓扑的变流器一次开关动作输出相电压可产生超过Udc/2的电压跳变,而不会造成功率开关器件过电压损坏[18]。例如,当桥臂开关状态由+1跳变为-1时,上桥臂的开关管不会因承受过电压而损坏。因此,与传统NPC三电平拓扑变流器相比,T型三电平变流器一次开关动作27条空间电压矢量均可自由切换。相应地,图2中下一开关周期可选电压矢量对应的点表示为实心点。
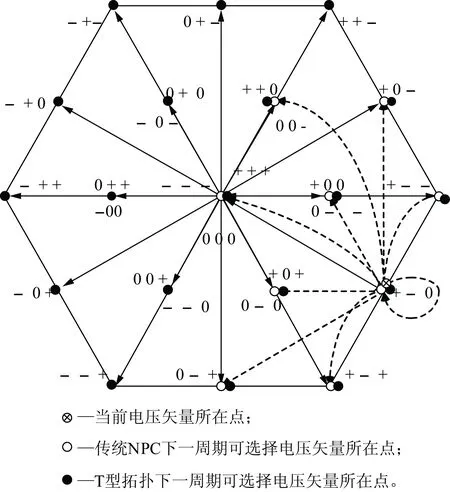
图2 三电平变流器电压矢量跳变原理图
2 MPC算法与几何分析
2.1 MPC算法的原理及实现
T型三电平储能变流器的功率控制可归纳为多目标约束优化控制问题,其中多目标分别指有功功率、无功功率及中点电位控制目标。前文已根据T型三电平储能变流器被控制量有功功率P、无功功率Q、中点电位Uo与桥臂开关函数S的关系构建该变流器系统的预测模型f{P,S}、f{Q,S}、f{Uo,S}。
处理一个有约束的多目标优化问题,传统方法通过在各个目标函数间配置不同权值函数,从而将多目标转化为单一目标函数优化问题。本文降低对预测目标的精确性要求,即保证预测误差在一定允许值之内以扩大最优解的存在范围,将多目标预测由复杂的耦合控制变为各目标的单独控制,从而得到更多的控制自由度。具体以有功功率控制为例介绍该种算法。
图3为基于有功功率控制的模型预测控制原理,其给定有功功率参考值为Pref,当前时刻tk该储能变流器输出有功功率值为Pk。
根据式(8)采用遍历法可得不同开关状态S对应的下一时刻有功功率预测值Pk+1,允许预测值与参考值最大偏差的绝对值为P0(P0>0),图3中阴影部分的有功功率预测值即满足控制要求。定义基于有功功率预测控制的偏差函数为
(11)
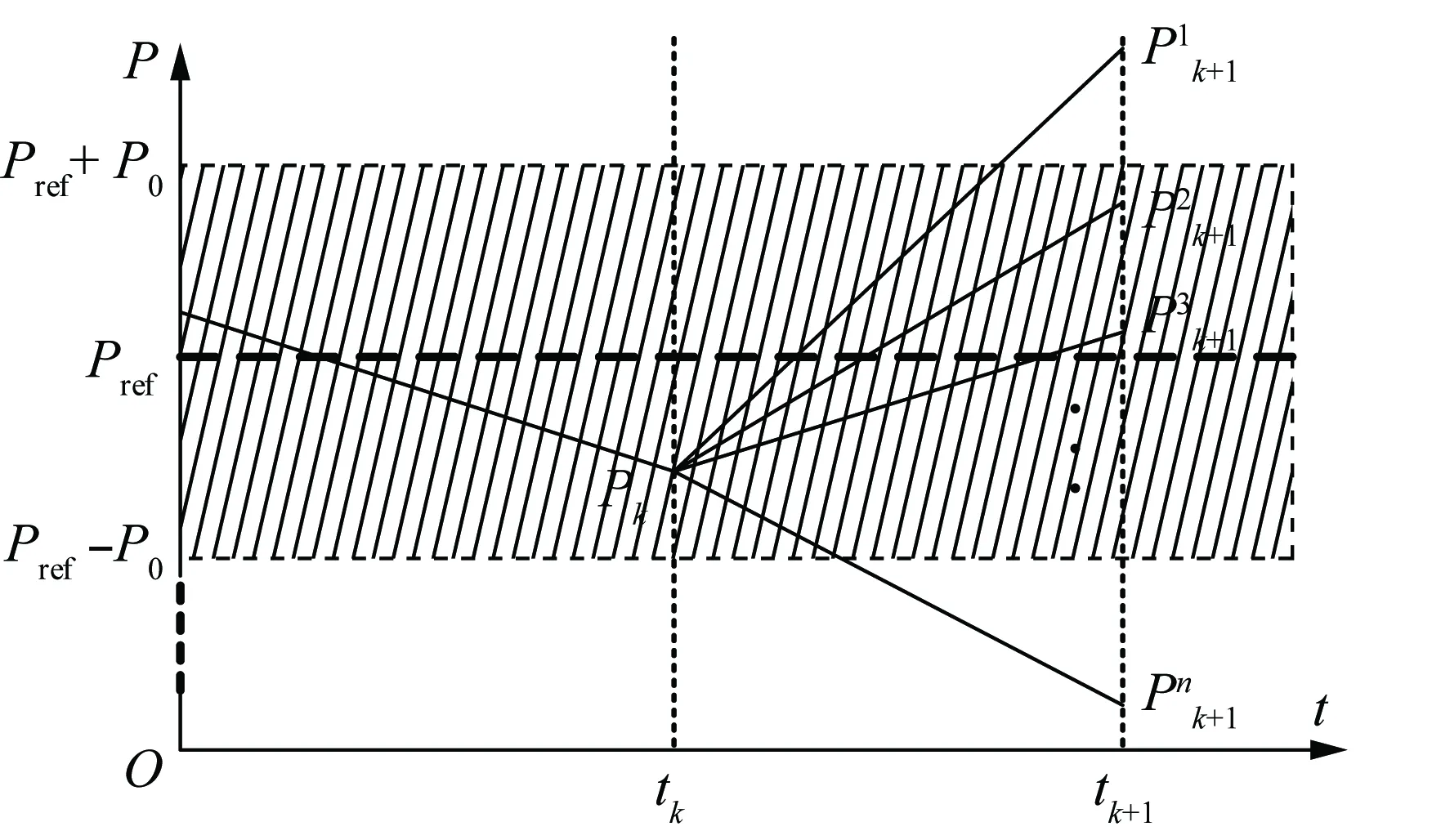
图3 MPC算法的有功功率控制原理图
式中△P为预测输出有功功率与其参考值之间的偏差。
有功功率最大偏差大于允许值P0时,其偏差函数值εP随偏差|△P|线性增大。同理可定义无功功率Q和中点电位Uo的偏差函数εQ、εU。储能变流器3个控制指标均达到要求即为三者对应的偏差函数均为0的情况,此时选取任意满足该条件的开关函数S均可实现控制目标。若无法找到实现控制目标的开关函数S而造成优化无解的状况,则采用权值法将原控制目标的偏差函数相加得到综合偏差函数为
(12)
选取使综合偏差函数值最小的开关函数S作为最优解。上述模型预测控制算法对应的流程如图4所示。
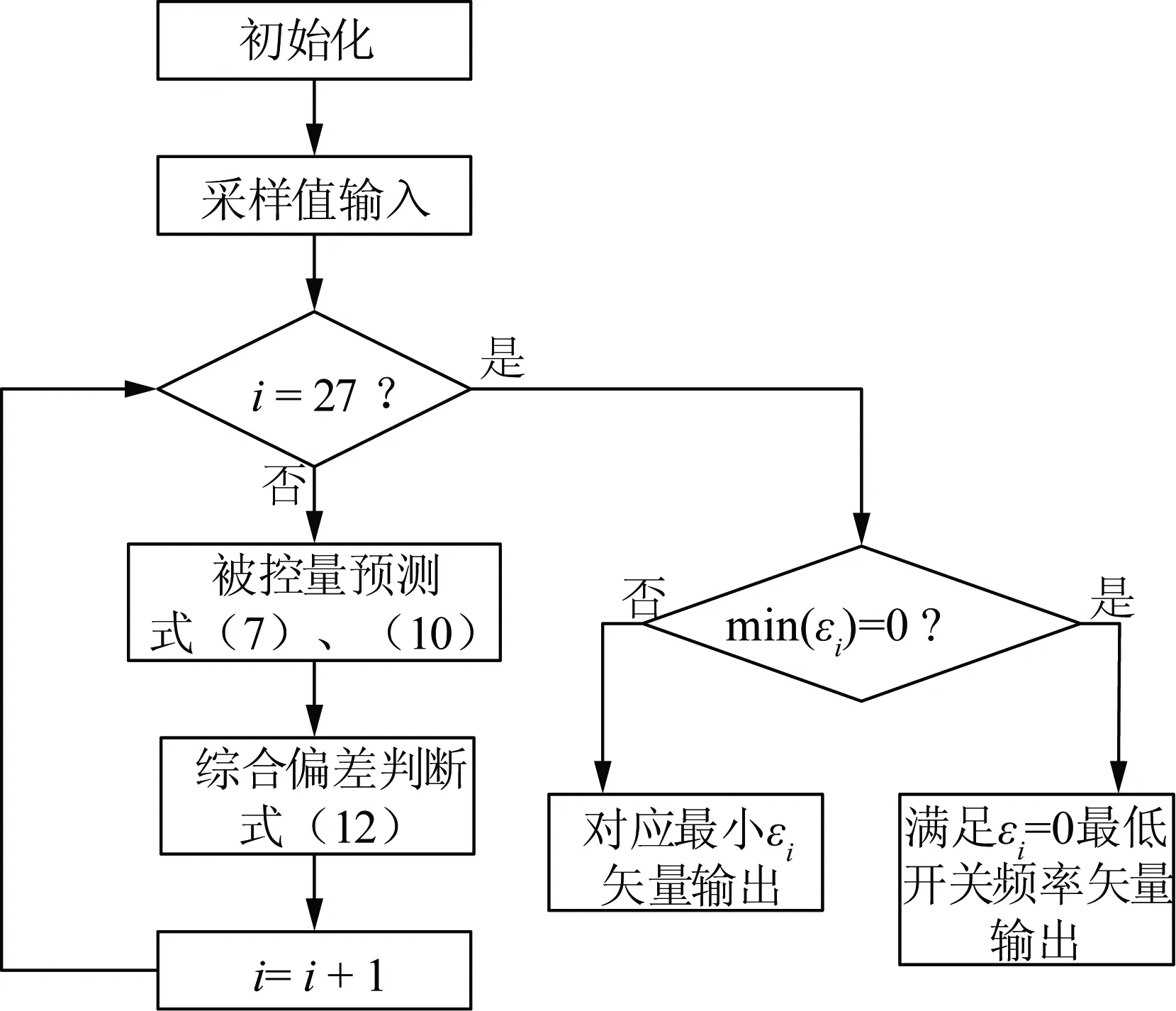
图4 MPC算法流程图
2.2 几何分析
T型三电平拓扑储能变流器与NPC拓扑相比,优势在于输出电压跳变范围可超过Udc/2,而不造成功率开关器件损坏。输出电压矢量图上,这种优势体现在T型三电平储能变流器下一时刻输出可以是任意离散电压矢量,而不局限在当前时刻电压矢量周围。下面采用几何法分析T型三电平储能变流器这种优势对其功率预测控制的影响。
三电平拓扑变流器输出电压矢量位于以0矢量为中心的正六边形区域,图5为两相静止αβ坐标系下的功率变化及电压矢量分布图,可用以分析不同位置电压矢量对变流器输出功率的影响。
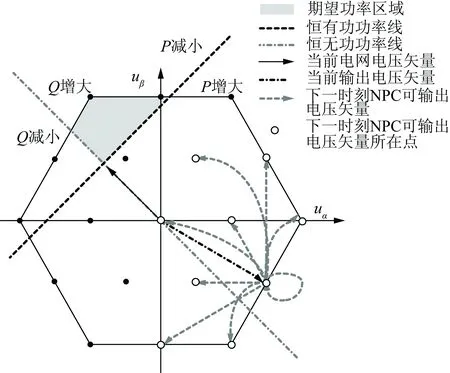
图5 功率变化及电压矢量分布图
首先分析不同位置电压矢量对有功功率的影响。当前时刻电网电压矢量可通过传感器采样得到,即为已知量。令式(6)中有功功率变化率为0,则有
(13)
忽略式(13)中ωQ及RP项,可进一步化简得:
(14)
将式(14)中uα、uβ分别对应到图5中横坐标与纵坐标,则式(14)可表示为图5中一条垂直于电网电压矢量的直线。定义该直线为恒有功功率线,其中分布于该直线上的电压矢量不改变系统有功功率,而分布于该直线上方的电压矢量可减小系统有功功率,下方的电压矢量可增大有功功率。
分析恒无功功率线与上述过程类似,同样令式(6)中无功功率变化率为0,并忽略其中较小的量可得对应的恒无功功率线:
(15)
此时恒无功功率线为一条经过坐标原点且与电网电压矢量垂直的直线。分布于该直线上方的矢量可增大系统无功功率,反之下方的矢量可减小系统无功功率。
根据上述分析可知,电压空间矢量所在平面区域可被分为4个部分,分别对应有功功率及无功功率的增大与减小。恒功率线分布如图5所示,此时系统若需要有功功率减小同时无功功率增大,则下一时刻变流器输出电压矢量必须位于图中阴影部分。对于NPC拓扑三电平储能变流器,其下一时刻可输出电压矢量只能分布在当前时刻电压矢量周围,而不能处于所需调取的阴影区域使得有功、无功功率预测控制的偏差函数不同时为0,即模型预测控制结果不在满意范围之内。对于T型三电平拓扑储能变流器,下一时刻可输出图5中任意电压矢量,从而在满意范围内跟踪有功功率及无功功率指令。T型三电平拓扑储能变流器输出电压跳变范围大的特点在模型预测控制中表现为优化自由度更高。
3 仿真研究
为验证前文几何分析结果,在Matlab/Simulink环境中分别建立了NPC和T型拓扑的三电平储能变流器模型,表1给出基本参数。
表1 系统基本参数
Table 1 Basic parameters of system

图6给出稳态仿真波形,其中有功功率参考值为40 kW,无功功率参考值为0 kV·A。定义flag为每一控制周期内被控量不在期望控制区间的标志位,flag值为1表示综合偏差函数ε大于0,flag值为0表示ε为0。图6(a)所示为NPC三电平储能变流器稳态仿真波形,从图中可以看出,输出相电流含有大量谐波,有功、无功功率的跟随特性较差,并且标志位flag在绝大多数时间里值为1,这意味着被控量不在期望范围内。图6(b)给出T型三电平储能变流器稳态仿真波形,从图中可以看出,输出相电流谐波含量较小,有功、无功功率的跟随特性较好。此外,标志位flag只在个别时刻值为1,即被控量的满意度较高。
图7给出有功功率参考值由40 kW跳变为80 kW时的动态仿真波形。从图7(a)可以看出,NPC拓扑储能变流器输出电流谐波含量(总谐波畸变率为7.3%)及有功功率跟随误差相对较大。从图7(b)中可以看出,T型拓扑储能变流器输出电流谐波含量(总谐波畸变率为2.6%)及有功功率跟踪误差较小。此外,有功功率的响应时间约为1ms,其相应速度及跟随特性均优于NPC拓扑储能变流器。
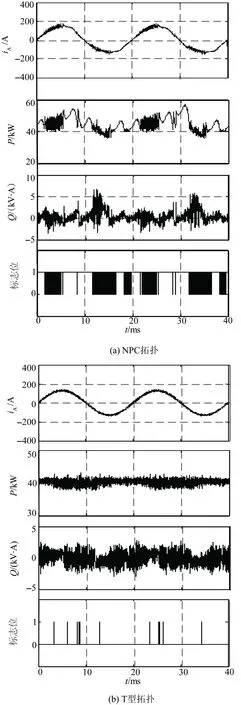
图6 稳态仿真波形
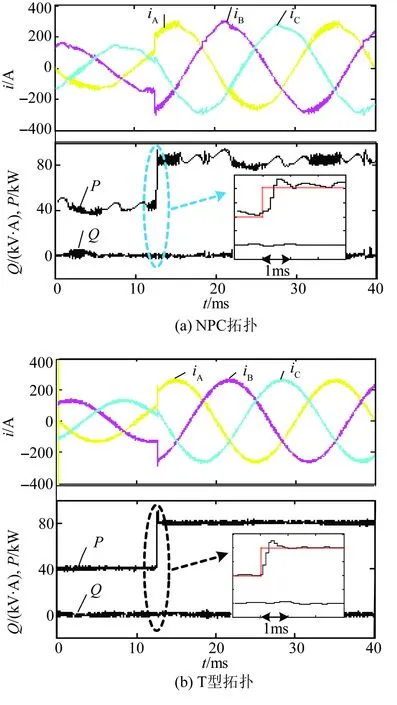
图7 动态仿真波形
4 结 论
本文提出T型三电平储能变流器的一种模型预测控制算法。与传统NPC三电平变流器相比,T型三电平储能变流器具有如下优势:
(1)T型三电平储能变流器输出电压跳变不受限制;
(2)相较NPC三电平拓扑采用的传统模型预测控制算法,所提基于T型三电平拓扑的模型预测控制算法可实现更为优越的稳态与暂态控制特性。
最后,采用几何分析方法证明了所提模型预测控制算法的优越性。仿真结果验证了理论分析的正确性与该控制算法的可行性。
[1]李德鑫, 董添, 常学飞, 等. 基于变权值自适应滤波的风光储协调优化控制[J]. 电力建设, 2015, 36(6): 32-37. LI Dexin, DONG Tian, CHANG Xuefei, et al. Optimal control of PV-wind-storage hybrid power system based on variable weight adaptive filtering [J]. Electric Power Construction, 2015, 36(6): 32-37.
[2]陈国恩, 宗鹏鹏, 朱伟, 等. 计及可再生能源与负荷互补特性的储能随机调度[J]. 电力建设, 2015,36(6): 27-33. CHEN Guoen, ZONG Pengpeng, ZHU Wei, et al. Stochastic dispatching of energy storage devices considering complementarity between renewable energy and load [J]. Electric Power Construction, 2015, 36(6): 27-33.
[3]陈跃燕, 李相俊, 韩晓娟, 等. 基于移动平均法和风电波动率约束的电池储能系统平滑风电出力控制策略[J]. 电力建设, 2013,34(7): 1-5. CHEN Yueyan, LI Xiangjun, HAN Xiaojuan, et al. Control strategy of smoothing wind power output using battery energy storage based on moving average method and wind power volatility rate constraint [J].Electric Power Construction, 2013, 34(7): 1-5.
[4]许守平,李相俊,惠东. 大规模电化学储能系统发展现状及示范应用总数[J]. 电力建设,2013,34(7): 73-80. XU Shouping, LI Xiangjun, HUI Dong. A review of development and demonstration application of large-scale electrochemical energy storage [J].Electric Power Construction, 2013, 34(7): 73-80.
[5]姜卫东, 杨柏旺, 黄静, 等. 不同零序电压注入的 NPC 三电平逆变器中点电位平衡算法的比较[J]. 中国电机工程学报, 2013, 33(33): 17-25. JIANG Weidong, YANG Bowang, HUANG Jing, et al. Comparisons of the neutral point voltage balancing algorithm for NPC three-level inverters based on different zero-sequence voltage injection [J]. Proceedings of the CSEE, 2013, 33(33): 17-25.
[6]NABAE A, TAKAHASHI I, AKAGI H. A new neutral-point-clamped PWM inverter[J]. IEEE Transactions on Industry Applications, 1981, 17(5): 518-523.
[7]SCHWEIZER M, KOLAR J W. Design and implementation of a highly efficient three-level T-type converter for low-voltage applications[J]. IEEE Transaltions on Power Electronics, 2013, 28(2):3680-3693.
[8]王付胜, 邵章平, 张兴, 等. 多机 T 型三电平光伏并网逆变器的环流抑制[J]. 中国电机工程学报, 2014, 34(1): 40-49. WANG Fusheng, SHAO Zhangping, ZHANG Xing, et al. Circulating current reduction for T-type three-level grid-connected photovoltaic inverters [J]. Proceedings of the CSEE, 34(1): 40-49.
[9]MALINOWSKI M, KAZMIERKOWSKI M P, TRZYNADLOWSKI A M. A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives[J]. IEEE Transactions on Power Electronics, 2003, 18(6): 1390-1396.
[10]MALINOWSKI M, KAZMIERKOWSKI M P, HANSEN S, et al. Virtual-flux-based direct power control of three-phase PWM rectifiers[J]. IEEE Transactions on Industry Applications, 2001, 37(4): 1019-1027.
[11]ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[12]CORTÉS P, KAZMIERKOWSKI M P, KENNEL R M, et al. Predictive control in power electronics and drives[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12): 4312-4324.
[14]沈坤, 章兢, 王坚, 等. 三相逆变器并联系统的无互连线预测控制[J]. 中国电机工程学报, 2013, 33(6): 46-53. SHEN Kun, ZHANG Jing, WANG Jian, et al. Wireless predictive control of parallel three-phase inverter systems [J]. Proceedings of the CSEE, 2013, 33(6): 46-53.
[15]方支剑, 段善旭, 陈天锦, 等. 储能逆变器预测控制误差形成机理及其抑制策略[J]. 中国电机工程学报, 2013, 33(30): 1-9. FANG Zhijian, DUAN Shanxu, CHEN Tianjin, et al. Formation mechanism and suppression strategy of prediction control error applied in a battery energy storage inverter [J]. Proceedings of the CSEE, 2013, 33(30): 1-9.
[16]杜少通, 伍小杰, 周娟, 等. 一种采用虚拟磁链模型预测的新型PWM算法[J]. 中国电机工程学报, 2015, 35(3): 688-694. DU Shaotong, WU Xiaojie, ZHOU Juan, et al. A novel algorithm of PWM using virtual flux model prediction [J]. Proceedings of the CSEE, 2015, 35(3): 688-694.
[17]曹晓冬, 谭国俊, 王从刚, 等. 一种低开关频率 PWM 整流器的满意预测控制策略[J]. 中国电机工程学报, 2013, 33(27): 69-77. CAO Xiaodong, TAN Guojun, WANG Conggang, et al. A research on low switching frequency PWM rectifiers with satisfactory and model predictive control [J], Proceedings of the CSEE, 2013, 33(27): 69-77.
[18]朱明正. T型三电平电池储能功率转换系统控制策略的研究[D]. 上海交通大学, 2014. ZHU Mingzheng. Research of control strategy of T-type three-level power conversion[J]. Shanghai: Shanghai Jiao Tong University, 2014.
(编辑 张小飞)
A Model Predictive Control Algorithm Suitable to Improve Power Response Characteristic of T-Type Three-Level Converter for Energy Storage
LIU Jianfeng,QIN Lulu
(College of Electrical Engineering, Shanghai University of Electric Power,Shanghai 200082,China)
Model predictive control (MPC) has been widely used in battery energy storage system. During each switching cycle of conventional neutral point clamped(NPC) three-level energy storage converter, its output voltage jumping can not exceed the half of the DC bus voltage, which will seriously affect the power response characteristics of the converter MPC. Therefor, this paper proposes the MPC algorithm based on T-type three-level converter for energy storage. Under the premise of ensuring the active power, reactive power and neutral point potential deviation of the converter, we adopt traversing method to obtain the output voltage vector with the minimum switching frequency of the converter, which gives full play to the advantages of no output voltage jump limitation of T-type three-level topology converter. Finally, we use geometric analysis method to compare the power control characteristics between T-type topology and NPC topology converters for energy storage. The analysis results show that the proposed MPC algorithm can greatly improve the power control characteristics of T-type three-level converter for energy storage.
energy storage; T-type three-level converter; NPC three-level converter; power control; model predictive control
TM 46
A
1000-7229(2016)11-0041-07
10.3969/j.issn.1000-7229.2016.11.007
2016-08-03
刘建锋(1968),男,博士,副教授,研究方向为智能变电站智能设备等;
秦露露(1991),女,硕士研究生,研究方向为智能配电网及其控制应用。
