考虑蓄电池空间分布的协调控制策略
2017-01-10李秀磊耿光飞
李秀磊,耿光飞
(中国农业大学信息与电气工程学院,北京市 100083)
考虑蓄电池空间分布的协调控制策略
李秀磊,耿光飞
(中国农业大学信息与电气工程学院,北京市 100083)
随着配电网不断的复杂化以及主动配电网、智能电网等概念的提出,在配电网中将可能有多个储能系统存在,而当前对储能系统的运行研究主要集中在时间上的优化,很少有涉及其在空间上的优化。提出一种两阶段蓄电池储能系统(battery energy storage system,BESS)运行控制策略制定方法:一阶段以储能套利与削峰收益之和最大为目标,根据分时电价划分充放电时间段,将所有储能系统看作一个整体,在时间周期上制定总的运行控制策略;二阶段在一阶段基础上进行空间二次优化,考虑网络结构,以降低网损所得收益最大为目标,对各储能系统在各时间段上的充放电功率进行分配。最后以修改的IEEE 33节点系统作为算例,验证了本文所提方法的有效性。
配电网;空间分布;蓄电池储能系统(BESS);协调控制策略
0 引 言
近年来,我国电力负荷增长迅速,电网规模不断扩大,负荷峰谷差也不断增大,与此同时,光伏、风电等以可再生能源发电的分布式电源(distributed generation, DG)大量接入电网,而DG出力具有间歇性和波动性,使得电力供需平衡问题变得更加突出。储能系统在一定程度上打破了电力供需实时平衡的限制,其具有削峰填谷、平滑间歇性电源功率波动、改善电压质量等作用[1-3]。
目前,储能技术主要分为机械储能、蓄电池储能(battery energy storage system,BESS)、电磁储能和热力储能4类[4],其中BESS具有充/放电速度快、效率高、使用寿命长、对地理条件要求低等优点,因而受到更多的关注和研究[5],特别是其在配电网中的研究。
很多学者对BESS的配置及运行问题进行了深入的研究,文献[5]考虑了BESS的充放电平衡约束、全寿命周期等因素,研究制定了配电网中BESS的运行策略。文献[6-8]在微电网中对BESS进行配置及运行研究,分别从风/光/柴/储的组合、超级电容器和蓄电池混合储能、储能系统平滑微电网联络线功率波动的角度进行了研究。文献[9]以在用户自建DG的配电网中,配电网公司投资建设BESS的经济效益为研究目标,讨论BESS的最优配置,并在配置过程中考虑运行策略。文献[10]考虑了配电网的网络结构,建立结合网损的BESS优化运行模型,并采用双层优化的方法进行求解。文献[11]面向供电能力提升,针对含DG的配电网储能功率进行了多级多目标动态优化。文献[12]提出了基于动态规划的BESS削峰填谷实时控制方法,能够在线修正优化结果,并且考虑到了充放电次数和放电深度对电池寿命的影响。文献[13]分别以负荷方差最小和负荷变化平方量最小为目标函数制定BESS运行策略,研究分析负荷曲线的优化情况。
上述文献中有关BESS的运行优化研究基本都是实时或者从时间周期上进行的时间上的优化,而随着配电网不断的复杂化以及主动配电网、智能电网等概念的提出,配电网中可能会有多个储能系统存在,如电动汽车充电站作为储能系统。此时多个BESS在空间上的协调优化运行对减少网络损耗将变得非常重要。现有文献中很少有涉及从时间和空间角度上对BESS进行运行优化的研究。
本文在现有文献的基础上从时间和空间的角度提出一种两阶段BESS优化运行策略制定方法:一阶段以BESS套利与削峰收益最大为目标,求得时间上优化运行结果;在一阶段优化结果的基础上,二阶段考虑系统网架,以降低网损所得收益最大为目标,求得空间上优化运行结果,即最后的优化运行结果。最后通过算例分析验证本文所提方法的有效性。
1 BESS数学模型
本文参考文献[6]中的方法,从荷电状态(stage of charge,SOC)等方面建立数学模型,具体模型如式(1)—(2)所示,其中式(1)表示充电过程,式(2)表示放电过程。
(1)
(2)
式中:t为仿真时刻;Δt为采样间隔,本文取1 h;ε表示BESS剩余电量每小时的损失率,简称自放电率;Pess,c(t)、Pess,dis(t)分别表示BESS充、放电功率大小;α和β分别表示BESS充、放电效率;Ee为BESS的容量。
蓄电池充放电过程中具有一定的约束,为避免电池过充过放,SOC有一定范围限制,蓄电池不能将电量全部放完也不能完全充满。
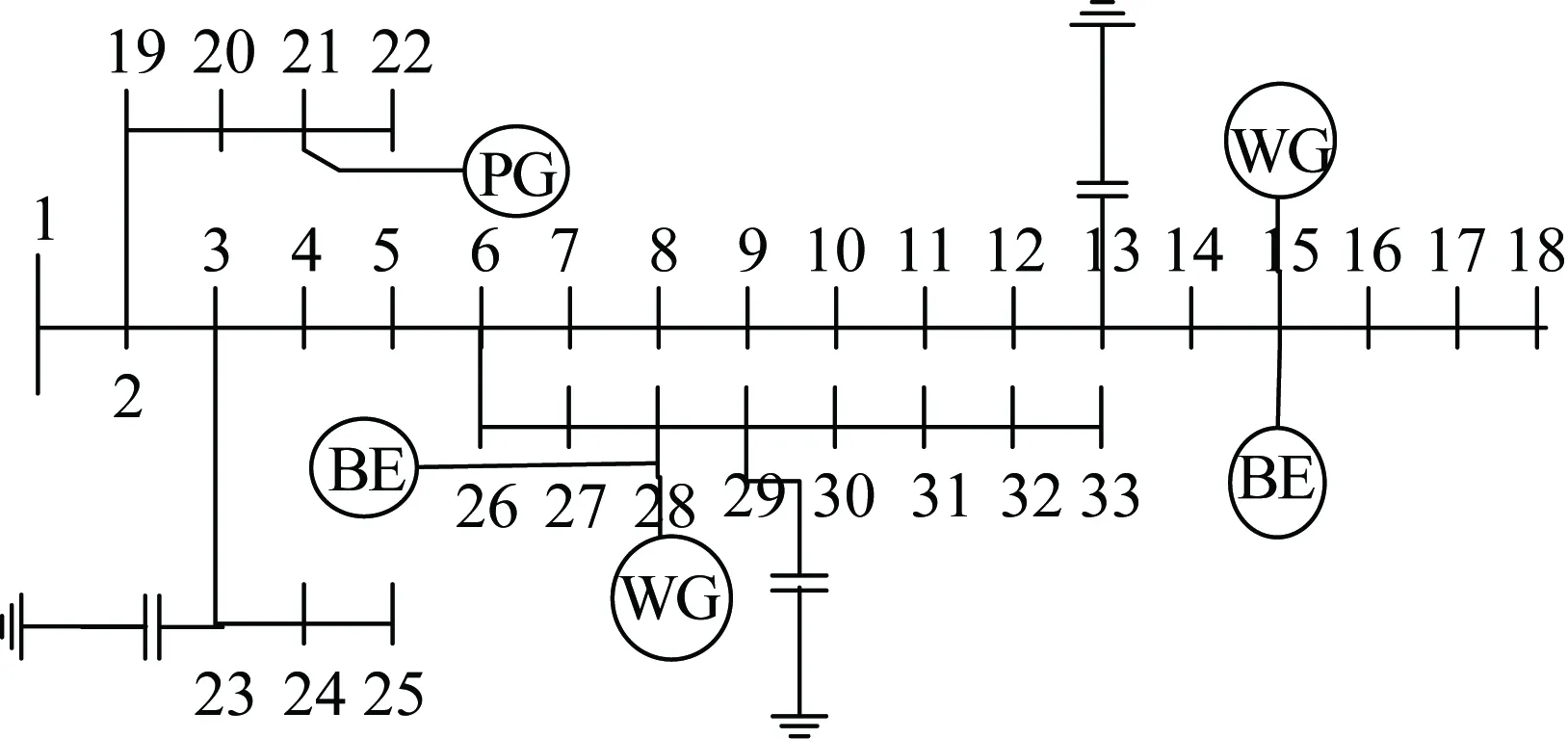
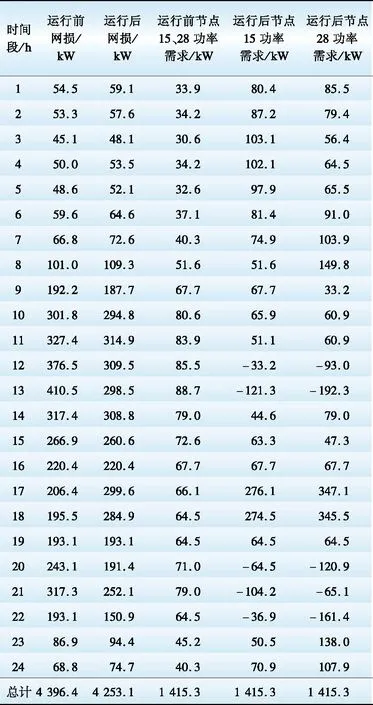
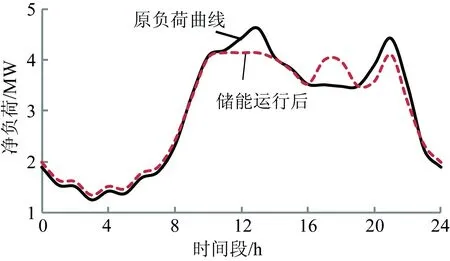
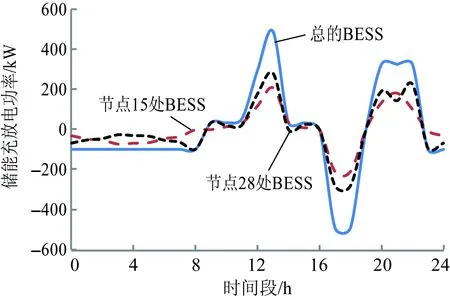
CSOC,min (3) -Pess,c,max (4) 式中:CSOC,min和CSOC,max分别为电池荷电状态的最小值和最大值;Pess,c,max和Pess,dis,max分别表示电池最大允许充电功率和最大允许放电功率,负号表示电池充电。 2.1 时间优化运行策略 根据分时电价[14]进行充放电时间段的划分,高电价时段为放电时间,低电价时段为充电时间。为提高储能系统的利用率,对于平电价时段,若其前后时段都为高电价时段,则为充电时间;若其前后时段都为低电价时段,则为放电时间;其余情况电池为空闲状态或看作以0功率充放电。 本文所提的时间上的优化运行控制策略是将系统中所有的BESS看作一个统一的整体,然后对其进行统一的运行控制。 2.1.1 目标函数 优化的目标是在系统安全稳定的基础上实现经济效益最大化,具体目标函数为 max f(P1,P2,···,P24)=Cs+Cd (5) 式中:P1,P2,…,P24为BESS在24个时段上的充放电功率,是控制变量;Cs为BESS 1天的低储高放套利;Cd为BESS运行后折合到1天的配电网降低峰荷收益。Cs的计算公式为: Cs=Cs,dis-Cs,c (6) (7) (8) 式中:Cs,dis和Cs,c分别为BESS 1天的放电收入费用和充电支出费用;N为BESS的个数;mdis和mch分别为BESS的放电电价和充电电价,都为对应时段处的分时电价;Pess,i,dis(t)和Pess,i,c(t)分别为BESS在t时刻的放电功率和充电功率,每个时刻的充放电状态都是确定的,负数表示充电,正数表示放电。 Cd的计算公式为 (9) 式中:pd为引入BESS后的削峰值(变电站可避免容量);θ为变电站单位容量的综合投资费用;Ck为变电站资金等年值系数,其表达式为 (10) 式中r和h分别为变电站的年贴现率和使用年限。 此部分的降低峰荷收益主要是指延缓配电网升级改造的收益,为简化计算,本文只考虑在变电站需要扩容的情况下,延缓其改造的收益。 2.1.2 约束条件 (1)日周期内充、放电能量守恒约束: (11) (2)BESS充放电时的约束。各时刻SOC约束和充放电功率约束,如式(3)—(4)所示。 (3)连续充、放电时段间的SOC约束。为使得求解的充放电策略是全局最优解,相邻连续充放电时间段内,SOC有一定约束。 CSOC,dis,i≤CSOC,c,i (12) 式中:CSOC,dis,i为第i个连续充电时间段后与其相邻的第i个连续放电时间段可放电量占总容量的水平;CSOC,c,i为第i个连续充电时间段,充完电后的剩余电量水平。 2.2 空间优化运行策略 本文所提BESS空间上的优化运行策略是建立在2.1节时间优化运行结果基础上的,具体是对各个BESS在各时间段上的充放电功率进行分配。 2.2.1 目标函数 (13) 式中:pi,1,pi,2,…,pi,24表示N个BESS分别在1—24个时段上的充放电功率;Ploss1(t)和Ploss2(t)分别为BESS运行前、后在第t个采样间隔内配电网的有功线损;ma为向大电网购电电价。 2.2.2 约束条件 (1)节点电压约束: Uimin≤Ui≤Uimax,i=1,2,3,···,b (14) 式中:Uimin和Uimax分别为第i节点处电压Ui的下限和上限;b为配电网节点总数。节点电压约束是电能质量对BESS运行的要求。 (2)支路电流约束: Ii≤Iimax,i=1,2,3,···,n (15) 式中:Iimax为第i条支路电流Ii的上限;n为支路总数。支路电流约束是系统安全稳定对BESS运行的要求。 (3)潮流方程约束: (16) 式中:PG,i、QG,i分别为节点i处电源的有功和无功出力;PL,i、QL,i分别为节点i处的有功和无功负荷;Ui、Uj分别为节点i和节点j的电压幅值;Gij、Bij分别为节点导纳矩阵元素的实部和虚部;θij为节点i和节点j的电压相角差。 (4)充放电功率约束。因为本文的优化计算是在时间优化结果基础上进行的,所以,BESS的充放电功率有一定约束,即 (17) 式中pi,t表示第i个BESS在第t个时段上的充放电功率。 (5)SOC相关约束。各时刻处的SOC约束,如式(3)所示。连续充、放电时段间的SOC约束如式(18)所示: CSOC,k,dis,i≤CSOC,k,c,i, k=1,2,3,···,N (18) 式中:CSOC,k,dis,i为第k个BESS的第i个连续充电时间段,充完电后的剩余电量水平;CSOC,k,c,i为第k个BESS的第i个连续充电时间段后与其相邻的第i个连续放电时间段可放电量占总容量的水平。 3.1 算例描述 为验证本文所提运行策略的有效性,以IEEE 33节点配电系统[15]作为算例,并在节点15、21和28上分别增加了300 kW风力DG、400 kW光伏DG和400 kW风力DG,节点13、23和29分别增加了0.9 MV·A、0.8 MV·A和0.8 MV·A的电容器,节点15和节点28上分别配有容量为420 kW·h和562 kW·h的BESS,系统结构如图1所示,制定该系统中BESS运行策略。算例系统中,DG、电容器、BESS位置和容量参照文献[16-17]进行确定。对于各小时节点处的功率数据,以对应小时段内的平均功率等效,某地典型日的DG出力和典型日负荷曲线如图2所示。 图1 BESS的配电网算例系统 图2 负荷曲线和DG出力曲线 [18]设定分时电价,高峰时段:09:00—15:00和20:00—22:00,高电价为1.0元/( kW·h);低谷时段:01:00—07:00,低电价为 0.35元/( kW·h);其余时段的平电价为0.55元/( kW·h)。电压波动的上下限为±7%,支路电流上限取BESS运行前支路电流的1.5倍,单个蓄电池储能单元 (1 kW·h)最大充、放电功率均为0.5 kW,最小和最大SOC分别为10%和90%,充、放电效率均为95%,剩余电量损失率为10%。 3.2 算例分析 本文采用MATLAB优化工具箱中的fmincon求解器求解所建模型。该求解器对初始值的选择无任何要求,收敛速度快,使用简便,结果准确。 按本文方法对算例进行求解。BESS运行前和空间上对BESS优化运行后各时段上的网损值以及节点15和节点28处的功率需求值如表1所示,其中BESS运行后的节点功率需求值为该节点处负荷需求与BESS输出功率叠加后的等效功率需求值。一阶段时间周期上和二阶段空间上依次优化后BESS的经济收益情况如表2所示。一阶段时间周期上对BESS优化运行后的负荷曲线变化情况如图3所示。二阶段空间上对BESS优化运行后的储能充放电功率曲线如图4所示,正数表示BESS放电,负数表示BESS充电。 表1 BESS运行前后各小时段网损值以及节点15、28处的功率需求值/ Table 1 Network loss value at each hour period and power curve of nodes 15 and 28 before and after BESS operation 注:算例原始数据中节点15和节点28各时段的负荷需求相同(无BESS运行时),各功率需求数据为对应时间段的平均功率。 表2 BESS运行后的经济收益 Table 2 Economic benefits after operation of BESS 元 由表1可以看出,BESS运行后与运行前相比,各时段上的网损值有的增加,有的减少,还有的不变,但1天24 h总的网损值减少了143.3 kW。BESS运行前节点15和28处各小时段的负荷需求侧值是相同的,经二阶段空间上优化计算后,在一定约束下对两节点处的BESS功率进行了最优分配,BESS运行后两节点上各小时段的等效负荷需求值不再相同,且都有负数出现(负数说明该小时段处BESS放电功率大于负荷需求值),因BESS日周期内的充、放电功率是平衡的,所以BESS运行前后节点15、28处的总的负荷需求值都不变。 图3 BESS运行前后负荷曲线变化情况 图4 BESS充放电功率曲线 从图3中可以看出,时间周期上优化后BESS有明显的削峰填谷作用,对应表2中的相关数据可知,优化后的总收益为 1 131.3元/d,相当可观。 从图4中可以看出,总的BESS与各BESS的充放电功率曲线变化趋势基本是相同的,这是因为二阶段空间优化是在一阶段时间优化运行的基础上进行的,是在一定条件下将总BESS功率分配给各BESS。由算例分析可知,节点28处的BESS安装容量比节点15处的大,但在时间周期内并不是所有时段内都是节点28处BESS充放电功率大于节点15处,二者的大小关系是交替变化的,这是因为各节点负荷值在空间分布上是不均的,各BESS在空间上出力相互配合才能最大限度地减小网络损耗。对应表2相关数据可知,空间优化后BESS每天的降损收益为78.8元。 本文提出一种两阶段储能系统运行控制策略制定方法,该方法在时间周期上能有效发挥BESS的削峰填谷作用,在空间结构上,多个BESS充放电功率能相互协调配合,有效降低网络中的能量损耗。因文章篇幅有限,本文并未研究多个BESS在时间和空间上同时优化的过程。下一步将研究建立多个BESS在时间和空间同时优化运行的数学模型,并与本文两阶段优化方法对比。 [1]廖怀庆,刘东,黄玉辉,等.考虑新能源发电与储能装置接入的智能电网转供能力分析[J].中国电机工程学报,2012,32(16):9-16. LIAO Huaiqing,LIU Dong,HUANG Yuhui,et al.Smart grid power transfer capability analysis considering integrated renewable energy resources and energy storage systems[J].Proceedings of the CSEE,2012,32(16):9-16. [2]苏小林,李丹丹,阎晓霞,等.储能技术在电力系统中的应用分析[J].电力建设,2016,37(8):24-32. SU Xiaolin,LI Dandan,YAN Xiaoxia,et al.Application analysis of energy storage technology in power system[J].Electric Power Construction, 2016,37(8):24-32. [3]李丹丹,苏小林,阎晓霞,等.储能优化配置关键问题分析[J].电力建设,2016,37(9):70-78. LI Dandan,SU Xiaolin,YAN Xiaoxia,et al.Principal problems of energy storage optimization allocation[J].Electric Power Construction, 2016,37(9):70-78. [4]王宁,张建成.基于能量协调控制的混合储能系统容量配置方法[J].电力建设,2016,37(8):72-77. WANG Ning,ZHANG Jiancheng.Capacity allocation method of hybrid energy storage systembased on energy coordination control[J].Electric Power Construction,2016,37(8):72-77. [5]向育鹏,卫志农,孙国强,等.基于全寿命周期成本的配电网蓄电池储能系统的优化配置[J].电网技术,2015,39(1):264-270. XIANG Yupeng,WEI Zhinong,SUN Guoqiang,et al.Life cycle cost based optimal configuration of battery energy storage system in distribution network[J].Power System Technology,2015,39(1):264-270. [6]丁明,王波,赵波,等.独立风光柴储微网系统容量优化配置[J].电网技术,2013,37(3):575-581. DING Ming,WANG Bo,ZHAO Bo,et al.Configuration optimization of capacity of standalone PV-wind-diesel-battery hybrid microgrid[J].Power System Technology,2013,37(3):575-581. [7]李成,杨秀,张美霞,等.基于成本分析的超级电容器和蓄电池混合储能优化配置方案[J].电力系统自动化,2013,37(18):20-24. LI Cheng,YANG Xiu,ZHANG Meixia,et al.Optimal configuration scheme for hybrid energy storage system of super-capacitors and batteries based on cost analysis[J].Automation of Electric Power Systems,2013,37(18):20-24. [8]王成山,于波,肖俊,等,平滑微电网联络线功率波动的储能系统容量优化方法[J].电力系统自动化,2013,37(3):12-17. WANG Chengshan,YU Bo,XIAO Jun,et al.An energy storage system capacity optimization method for microgrid tie-line power flow stabilization[J].Automation of Electric Power Systems,2013,37(3):12-17. [9]刘文霞,牛淑娅,石道桂,等.考虑运行策略及投资主体利益的主动配电系统储能优化配置[J].电网技术,2015,39(10):2697-2704. LIU Wenxia,NIU Shuya,SHI Daogui,et al.Optimal allocation of ADS battery energy storage considering operation strategy and investment subject benefit[J].Power System Technology,2015,39(10):2697-2704. [10]章美丹,宋晓喆,辛焕海,等.计及网损的配电网电池储能站优化运行策略[J].电网技术,2013,37(8):2123-2128. ZHANG Meidan,SONG Xiaozhe,XIN Huanhai,et al.Optimal operation strategy of battery energy storage system in distribution networks with consideration of power losses[J].Power System Technology,2013,37(8):2123-2128. [11]国宗,韦钢,郭运城,等.面向供电能力提升的配电网储能功率动态优化[J].电力系统保护与控制, 2015,43(19):1-8. GUO Zong,WEI Gang,GUO Yuncheng,et al.Dynamic optimization of energy storage power in distribution network based on power supply capacity[J].Power System Protection and Control,2015,43(19):1-8. [12]鲍冠南,陆超,袁志昌,等.基于动态规划的电池储能系统削峰填谷实时优化[J].电力系统自动化,2012,36(12):11-16. BAO Guannan,LU Chao,YUAN Zhichang,et al.Load shift real-time optimization strategy of battery energy stoyage system based on dynamic programming[J].Automation of Electric Power Systems,2012,36(12):11-16. [13]杨玉青,牛利勇,田立亭,等.考虑负荷优化控制的区域配电网储能配置[J].电网技术,2015,39(4):1019-1025. YANG Yuqing,NIU Liyong,TIAN Liting,et al.Configuration of energy storage devices in regional distribution network considering optimal load control[J].Power System Technology,2015,39(4):1019-1025. [14]阮文骏,王蓓蓓,李扬,等.峰谷分时电价下的用户响应行为研究[J].电网技术,2012,36(7):86-93. RUAN Wenjun,WANG Beibei,LI Yang,et al.Customer response behavior in time-of-use price[J],Power System Technology,2012,36(7):86-93. [15]王守相,王成山.现代配电系统分析[M].北京:高等教育出版社,2007:196-202. WANG Shouxiang,WANG Chengshan.Modern distribution system analysis[M].Beijing:Higher Education Press,2007:196-202. [16]刘公博,颜文涛,张文斌,等.含分布式电源的配电网动态无功优化调度方法[J].电力系统自动化,2015,39(15):49-54. LIU Gongbo,YAN Wentao,ZHANG Wenbin,et al.Optimization and dispatching method of dynamic reactive power in distribution network with distributed generators[J].Automation of Electric Power Systems,2015,39(15):49-54. [17]段开锋.电池储能系统在配电网中的应用研究[D].北京:北京交通大学,2014. DUAN Kaifeng,The application of battery energy storage system in the distribution network[D].Beijing:Beijing Jiaotong University,2014. [18]陈沧杨,胡博,谢开贵,等.计入电力系统可靠性与购电风险的峰谷分时电价模型[J].电网技术,2014,38(8):2141-2148. CHEN Cangyang,HU Bo,XIE Kaigui,et al.A peak-valley TOU price model considering power system reliability andpower purchase risk[J].Power System Technology,2014,38(8):2141-2148. (编辑 景贺峰) Coordinated Control Strategy Considering Spatial Distribution of Storage Battery LI Xiulei, GENG Guangfei (College of Information and Electrical Engineering, China Agricultural University, Beijing 100083, China) With the continuous complexity of distribution network, and the concepts of active distribution network, smart grid, there may be a number of energy storage systems in distribution network. However, the current researches on the operation of energy storage system are mainly focused on the optimization of time, and there are few of them involved in the optimization of the space. This paper presents a method for the control strategy of the two-stage energy storage system operation: in the first stage, it is the goal of the maximum benefit of the energy storage arbitrage and peak clipping, divides the time period of charging and discharging according to time-of-use price, all the energy storage systems are considered as a whole, and the total operation control strategy is formulated in the time period; the second stage is the second optimization of the space on the basis of the first stage, taking into account the network structure, the objective function is the maximum of the benefit of saving energy, the charging and discharging power of each energy storage system in each time period are distributed. Finally, a modified IEEE 33 node system is used as an example to verify the effectiveness of the proposed method. distribution network; spatial distribution; battery energy storage system(BESS); corrdinated control strategy TM 732 A 1000-7229(2016)11-0035-06 10.3969/j.issn.1000-7229.2016.11.006 2016-06-25 李秀磊(1990),男,硕士研究生,主要从事配电网中蓄电池储能和需求侧响应方面的研究工作; 耿光飞(1970),男,博士,副教授,本文通信作者,主要从事电力系统优化规划等方面的研究工作。2 BESS运行控制策略
3 算例分析


4 结 语
5 参考文献
