上承式异型拱桥拱轴线的选型
2017-01-10王银刚
王银刚
(中铁第四勘察设计院集团有限公司, 湖北 武汉 430063)
上承式异型拱桥拱轴线的选型
王银刚
(中铁第四勘察设计院集团有限公司, 湖北 武汉 430063)
研究上承式异型拱的结构受力特征以及其与对称拱在受力上的差异,引入“异型系数”来描述异型拱的不规则程度,大量算例表明,几种常用的拱轴线中,在不同异型系数和不同矢跨比下,上承式异型拱的拱轴线采用“悬链线(大拱侧)+抛物线(小拱侧)”组合时拱内弯矩最小。
拱桥; 异型拱; 拱轴线; 非对称拱; 不规则拱; 上承式拱
0 引言
异型拱由于其独特的美学造型,常见于城市景观桥。目前国内已建成多座异型拱桥,如安阳市东风桥、哈尔滨宽城桥等,这些异型拱桥均为下承式系杆拱,但对于上承式异型拱,其应用几乎为空白。在一些对景观要求较高的区域,上承式异型拱也常作为桥梁方案比选的对象之一,图1为三跨上承式异型拱和对称拱的外观比较,异型拱的组合使画面富有动态变化,改善了对称拱组合重心离散的缺陷,并可根据美的比例协调法则进行结构重心的调整,同时其强烈的动势效果使其在形态上产生了栩栩如生的生命感[1]。

图1 对称拱和异型拱造型比较
目前有关异型拱的科技文献[1-4]大都是以系杆拱为研究对象,鲜有提及上承式异型拱。文献[5]建立了2个异型圆弧拱和1个半圆形拱的有限元模型,分析了拱脚支承条件为固结和铰接时,这3个拱各自的周期、振型,以及在竖向荷载和水平荷载作用下的受力性能,为进一步研究异型拱提供了参考,但文中采用的算例较少,且未考虑不同拱轴线和不同矢跨比下的受力差异,因而得出的结论有限。
拱桥常用的拱轴线有圆弧线、抛物线和悬链线,拱轴线的形状直接影响主拱截面内力大小与分布,选择拱轴线的原则,也就是尽可能降低由于荷载产生的弯矩值。对于对称拱桥,主拱圈承受从拱顶向拱脚逐渐变大的均变荷载,其恒载压力线为一条悬链线,但对于异型拱,由于结构和荷载均不对称,几乎不存在一条理想的拱轴线吻合其恒载压力线,因此在常用的3种拱轴线中,选择一组合理的拱轴线来尽可能减小主拱圈的弯矩就显得尤为重要。
异型拱从外观来看可归纳为2种——类型Ⅰ和类型Ⅱ(分别见图1b和图1c的边拱),第Ⅱ类异型拱在小拱侧拱脚用了“回头”曲线,小拱拱脚承受了很大的弯矩,其受力明显不合理,且第Ⅱ类异型拱可通过在第Ⅰ类异型拱的拱脚加装饰实现,因此本文的研究对象为图1b所示的第Ⅰ类异型拱。
1 均变荷载下各类拱轴线的受力比较
上承式拱桥所受荷载为均变荷载,其荷载集度由拱顶向拱脚连续分布、逐渐增大,为了解异型拱与对称拱的受力差异,首先对异型拱取用3种常用的拱轴线,并分别对其施加同一荷载界面的均变荷载,查看主拱圈的弯矩和拱脚推力。
【算例1】:异型拱矢跨比f=1/5,跨径L=25 m,拱顶偏移桥跨中心线δ=2.95 m(图2)。主拱圈计算宽度为1 m,拱圈厚度为0.5 m,混凝土标号为C40,不计主拱圈的自重,拱脚采用固结。拱顶填土高1.5 m(对应悬链线拱轴系数m=4.33),拱轴线方程分别选用圆弧线、抛物线和悬链线,以同等跨径和矢跨比的对称拱计算结果作为比较。下面的讨论中称拱顶两侧跨度较大的拱为“大拱”,较小的拱为“小拱”。
从图3可以看出,在均变荷载下,悬链线异型拱大拱拱脚负弯矩较小,抛物线异型拱小拱拱脚正弯矩较小。与同等跨径的对称拱比较(表1)可知,异型拱的弯矩比对称拱大数倍不等,但两者的拱脚推力变化不大。
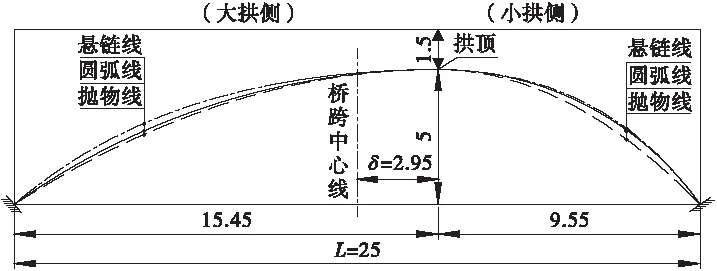
图2 算例1计算图示(单位: m)

图3 算例1中3种拱轴线下的弯矩图

表1 算例1中异型拱与同跨度对称拱的内力比较拱轴线弯矩/(kN·m)MminMmax拱脚推力/kN圆弧线异型拱-7658(147)4688(102)6995对称拱-16246986866抛物线异型拱-8723(168)3542(077)7009对称拱-308112826915悬链线异型拱-5206(10)4596(10)6803对称拱-3221136723注:括号内数值为系数。
2 均变荷载下的拱轴线组合
算例1的结果表明,在均变荷载下,异型拱大拱侧为悬链线时大拱所受弯矩值最小,大拱侧最佳拱轴线排名依次是:悬链线>圆弧线>抛物线;异型拱小拱侧拱轴线为抛物线时小拱侧的弯矩值最小,小拱侧最佳拱轴线排名依次是:抛物线>悬链线>圆弧线。是否存在大拱悬链线和小拱抛物线的组合,使得均变荷载下,拱内的弯矩值最小?下面分别建立9组有限元模型来考察不同拱轴线组合下,主拱圈的受力情况。
【算例2】: 将算例1中的异型拱的拱轴线采用圆弧线、抛物线和悬链线的两两组合,共9组组合结果。从表2中的计算结果可知,大拱拱轴线为悬链线时拱内弯矩、拱顶位移和拱脚推力均较优,与其他拱轴线比较来看,大拱拱轴线为圆弧线和抛物线时的拱内最大弯矩分别是悬链线的1.52倍和1.77倍,“悬链线(大拱)+抛物线(小拱)”的拱轴线组合为所有拱轴线组合中的最优组合。
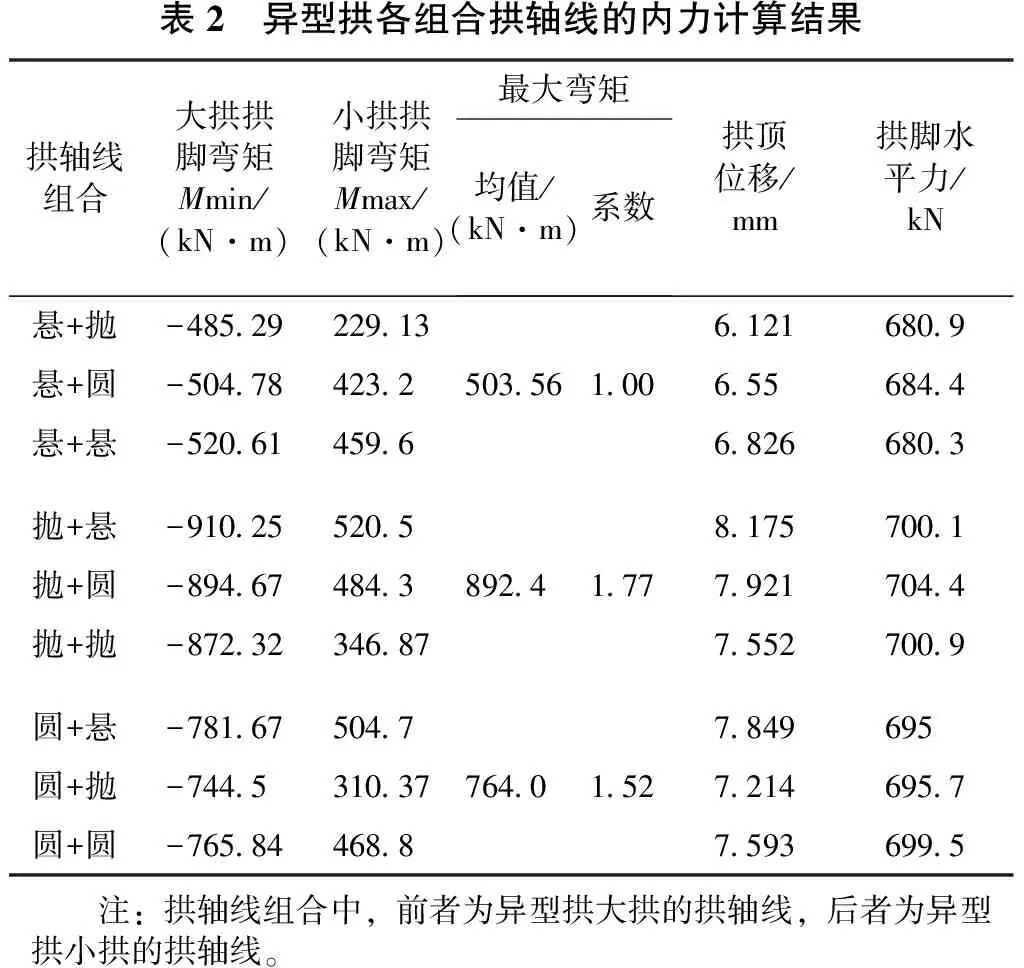
表2 异型拱各组合拱轴线的内力计算结果拱轴线组合大拱拱脚弯矩Mmin/(kN·m)小拱拱脚弯矩Mmax/(kN·m)最大弯矩均值/(kN·m)系数拱顶位移/mm拱脚水平力/kN悬+抛-485292291361216809悬+圆-504784232503561006556844悬+悬-52061459668266803抛+悬-91025520581757001抛+圆-894674843892417779217044抛+抛-872323468775527009圆+悬-7816750477849695圆+抛-744531037764015272146957圆+圆-76584468875936995 注:拱轴线组合中,前者为异型拱大拱的拱轴线,后者为异型拱小拱的拱轴线。
3 拱顶偏距与拱轴线的选择
以上的算例给定了拱顶偏移桥跨中心线的距离,得出的结论是对于上承式异型拱,拱轴线采用 “悬链线+抛物线”时拱内弯矩最小。我们知道对称悬链线拱在自重作用下,其压力线和拱轴线是重合的,异型拱内产生的弯矩主要是由于大拱和小拱侧的不平衡荷载引起,那么拱顶偏距的大小对拱内弯矩的影响将会很大。拱顶偏距的大小反映了异型拱的异型程度,为了将其与拱桥跨径联系起来,使这个度量更具普遍性,这里引入异型系数的概念,异型系数定义为异型拱大拱在拱脚连线上的投影距离与小拱在拱脚连线上的投影距离的比值,结合图2用公式表达如下:
(1)
式中:ξ为异型系数,其值≥1;L为拱桥跨径。
当拱顶偏距等于0时为对称拱,此时异型系数等于1,异型系数越大,拱的不规则程度越高。
下面通过调整拱顶偏移跨径中心线的距离δ分别进行计算,以寻求在不同δ下,拱轴线的选择与拱内弯矩的相关性,从之前的算例来看,上承式异型拱的大拱采用悬链线时,拱圈弯矩最小,因此下面的算例中,大拱的拱轴线均采用悬链线。
【算例3】: 将算例1中拱顶偏移桥跨中心线的距离δ分别取1.5、2.95、4.5、6 m,每一个δ用3种拱轴线组合进行计算,分别为“悬链线+圆弧线”、“悬链线+抛物线”、“悬链线+悬链线”,分析异型拱的受力。
3.1 拱顶偏距δ对主拱圈弯矩的影响
计算表明,异型拱主拱圈的弯矩图均为如图4的形式,考察弯矩图上4个特征位置处的弯矩值,分别为大拱拱脚弯矩M1、大拱拱腰弯矩M2、小拱拱腰弯矩M3、小拱拱脚弯矩M4,查看它们随拱顶偏距的变化情况。

图4 异型拱弯矩图

图5 拱圈特征点弯矩值随δ的变化曲线
从图5的计算结果,可以得出以下信息:
1) 所考察的4个特征点弯矩值均随δ的增加而增加,且呈现出规律的变化,可以用线性函数进行拟合。
2) 在各种拱轴线下,拱腰的弯矩M2、M3均小于大拱拱脚的弯矩M1,且随着δ的增加,拱腰弯矩值与大拱拱脚的弯矩值越来越离散,这表明在各种拱轴线下,拱腰的弯矩不控制设计。
3) 当δ增加到某一值时,“悬链线+圆弧线”拱的小拱拱脚弯矩值M4会超过M1成为主拱圈最大弯矩而控制设计,经最小二乘法拟合曲线方程并求出交点坐标为δ=5 m(对应异型系数ξ=2.33),即δ>5 m时,“悬链线+圆弧线”拱的弯矩由小拱拱脚控制。
4) “悬链线+抛物线”拱的小拱拱脚弯矩有超过大拱拱脚弯矩的趋势,经最小二乘法拟合曲线方程并求出交点坐标为δ=19.6 m,该值已超过拱的跨径,属区间外的解,无意义。因此可认为“悬链线+抛物线”拱的大拱拱脚弯矩为拱内最大弯矩。
5) 随着δ的增加,在所考察的4个弯矩特征值中,“悬链线+抛物线”拱的弯矩离散程度最小,这说明“悬链线+抛物线”拱的弯矩分布较另外2种拱轴线均匀。
下面在同一坐标系下比较3种拱轴线下的拱内最大弯矩情况,如图6所示。在3种拱轴线中,“悬链线+抛物线”拱的拱内弯矩最小。异型拱的拱内弯矩随异型系数的增大而增大,异型系数越大,拱的受压特征越弱,受弯特征越强。按现行《桥规》[6]进行偏心受压承载能力验算,在常规配筋下,当异型系数ξ=2.33时,其承载能力富余量仅为1.15。可见,在确定异型拱的异型系数时,还应考量主拱圈的偏心受压承载能力,若承载能力不足,则应增大主拱圈的截面尺寸或增强配筋。
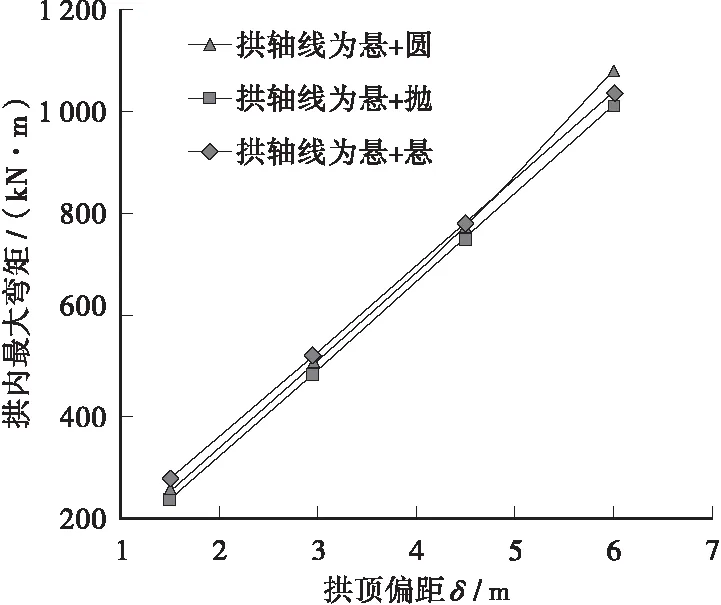
图6 拱内最大弯矩随δ的变化曲线
3.2 拱顶偏距δ对拱脚推力的影响
从图7中可知,拱脚推力随异型程度的增加而增大。在同一δ下,拱轴线的类型对拱脚推力的影响较小,当δ=6 m时,3组拱轴线的拱脚推力差异最大,拱脚推力最大与最小的比值仅为1.02。
对于同一拱轴线,在所选的几组算例中,δ=6 m和δ=1 m时的拱脚推力比值,“悬链线+圆弧线”为1.05,“悬链线+抛物线”为1.03,“悬链线+悬链线”为1.04。可见,在同一荷载边界下,异型拱的异型程度对拱脚推力的影响较小。
进一步地将图7中拱脚推力与等跨径对称悬链线拱的拱脚推力(表1)进行比较,可知两者最大的比值仅为1.06,粗略计算时,完全可以采用同等矢跨比的对称拱来预估异型拱的拱脚推力。

图7 拱脚推力随δ的变化曲线
3.3 拱顶偏距δ对拱顶位移的影响
异型拱主拱圈为偏心受压构件,在受荷较大的大拱侧拱腰产生了较大的竖向位移,从图8可知,拱顶偏距越大,拱圈的最大竖向位移也越大,“悬链线+抛物线”拱的竖向位移要比其余2种拱轴线的竖向位移小。
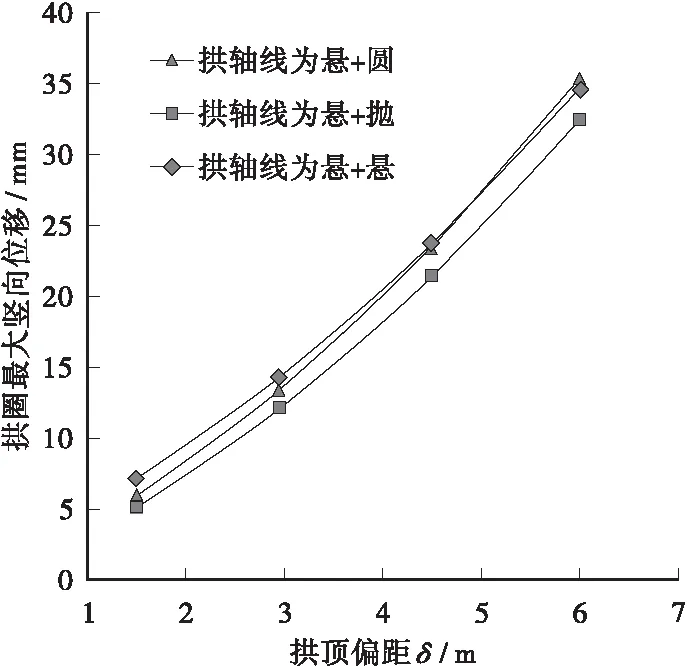
图8 拱内最大竖向位移随δ的变化曲线
4 矢跨比与拱轴线的选择
矢跨比是拱桥设计的重要指标,保持算例1中的其他参数不变,仅对矢跨比进行调整,以考察不同矢跨比下的最优拱轴线组合。从前面的算例来看,异型拱主拱圈的最大弯矩出现在大拱的拱脚,异型拱大拱采用的拱轴线类型对大拱的弯矩影响较大,而当大拱的拱轴线确定后,仅调整小拱的拱轴线类型,对整个主拱的最大弯矩值影响较小。上面已经讨论了大拱拱轴线采用悬链线是最优的,下面仅对大拱拱轴线为悬链线时进行细分,而以抛物线拱和圆弧拱的计算结果进行对照。
【算例4】: 调整主拱圈的矢跨比分别取f/L=0.12、0.16、0.2、0.24、0.28,其余条件同算例1,进行主拱圈内力计算,由于每种矢跨比所施加的荷载不一致,计算结果仅列出弯矩的比值(表3)。

表3 不同矢跨比下主拱圈弯矩计算结果(比值)矢跨比大拱拱脚弯矩(系数)悬+抛悬+悬悬+圆抛圆0121103101148141016110510216415102110710418015802411091061951610281112110210161小拱拱脚弯矩(系数)悬+抛悬+悬悬+圆抛圆11811351141471203165121182123121312923612602771383061290360146395 注:表中令拱轴线为“悬+抛”时的弯矩计算结果为1。
从图9可知,在各种矢跨比下,“悬链线+抛物线”拱的大拱所受的弯矩最小,“悬链线+抛物线”依然是最优的拱轴线组合,且这种拱轴线的优势随着矢跨比的增大而愈来愈明显。采用抛物线拱和圆弧线拱的受力状况均不如采用悬链线拱,其拱脚弯矩比悬链线拱大1.4倍以上。

图9 大拱拱脚弯矩随矢跨比的变化曲线
从图10可知,“悬链线+抛物线”拱的小拱拱脚弯矩值最小,且随着矢跨比的增大,这种拱轴线组合的优势也越来越明显,不过从工程设计的角度来说,只要小拱拱脚弯矩不超过拱内的最大弯矩(一般在大拱拱脚处),其拱轴线均可认为是合理的。

图10 小拱拱脚弯矩随矢跨比的变化曲线
5 结论
1) 文中以异型系数来反映异型拱的异型程度,可作为异型拱设计的一项重要的设计参数。异型系数越大,拱内弯矩也越大,拱顶位移也越大。异型系数对拱脚推力的影响较小,粗略计算时,其拱脚推力可按同等跨径和矢跨比的对称拱进行估算。
2) 在3种常用的拱轴线(圆弧线、抛物线、悬链线)中,异型拱的拱轴线选用“悬链线(大拱侧)+抛物线(小拱侧)”的组合为最优拱轴线。
3) 异型拱桥造型新颖,尤其适用于景观桥。在常规截面尺寸和常规配筋下,建议异型拱的异型系数不超过2.33。
[1] 李丽,李乔.对一种新型拱桥结构的美学分析及内力特性研究[J].四川建筑科学研究,2003,29(2).
[2] 李乔,李丽.异型拱桥结构内力分析[J].公路交通科技,2001,18(1):31-35.
[3] 黄侨,王宗林,李广义,等.异型拱结构的设计方法[J].东北公路,1994(3):50-54.
[4] 王会利,秦泗凤,张哲,等.斜跨异型拱桥的设计与分析[J].武汉理工大学学报(交通科学与工程版),2012,36(6):1157-1160.
[5] 马智刚,刘涛.对称与非对称拱面内受力性能研究[A].2010全国钢结构学术会议论文集[C].2010.
[6] JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
1008-844X(2016)04-0099-05
U 448.22
A
