线性时不变系统模型的建立及方框图法研究

张赜皓，姬五胜

（1.天津市中环系统工程有限责任公司，天津 300060；2.天津职业技术师范大学电子工程学院，天津 300222）

线性时不变系统模型的建立及方框图法研究

张赜皓1，姬五胜2

（1.天津市中环系统工程有限责任公司，天津 300060；2.天津职业技术师范大学电子工程学院，天津 300222）

利用算子将微分方程转换成系统函数，借助梅森公式对系统函数进行分解，提出一种画出分解后系统方框图的简单方法。该方法可应用于通信工程系统分析，在整体分析中起到辅助分析作用。利用系统方框图的分解将前向通道与反馈环路分别进行讨论，可以简化对复杂系统的直接分析，在一定程度上降低了系统分析的难度。通过数学分析证明了该方法的正确性。

线性时不变系统；微分方程；系统方框图

人类对微分方程的研究至今已有数百年的历史。自17世纪以来，伴随着微积分的发展，微分方程逐渐成为一门具有重要应用价值的学科。从早期对方向场的理解到今天关于微分方程定性理论的成熟知识体系，数百年的历史使这门数学分支不仅成为数学学科中综合性最强的领域之一，而且成为数学以外学科最为重要的分析工具。微积分发展极大地推动了通信技术、电子技术、生物技术等诸多领域的发展。在通信工程及相关系统工程中，将一个实际的物理系统模型化，抽象为数学表达式，便于研究系统的性能，如连续的线性时不变系统可以用常系数线性微分方程来描述和分析[1-2]。从工程应用方面考虑，有时需要对实际系统进行实验室模拟，画出系统的方框图是实现模拟实验的前提。因此，建立线性系统模型，对常系数线性微分方程进行分析，开展对系统时域与频域方框图法的研究非常必要。本文通过列写典型电路常系数线性微分方程，说明微分方程在通信工程等系统工程中进行实际电路分析的重要性；利用算子将微分方程转换成系统函数，进而借助梅森公式对系统函数进行分解，分别给出分解后的系统方框图及全系统方框图。本研究阐述了系统微分方程与系统方框图互换的方法，通过数学分析的方法证明了该方法的正确性。在必要情况下，利用系统方框图将前向通道与反馈环路分别进行讨论，在一定程度上可降低系统分析的难度。

1 模拟信号电路系统的时域分析和系统函数

模拟信号的时域分析方法不涉及任何变换，直接求解系统的微分、积分方程式，这种方法比较直观，物理概念清楚，是学习各种变换域方法的基础。变换域方法，如拉普拉斯变换具有分析简单的特点，已成为工程研究领域中重要的工具。

1.1 模拟信号电路系统微分方程的建立

模拟信号的系统参数若不随时间而改变，则该系统可以用线性常系数微分方程来描述。根据实际系统的物理特性可以列写出系统的微分方程，从而展开对实际系统的分析。下面给出一个例子[3]。

给定电路如图1所示。t＜0时开关S处于1的位置且已达到稳态；建立t=0时开关S由1转向2处i（t）电流的微分方程。

图1 实例电路原理图

根据电路形式所确定的回路电压方程和节点电流方程为：

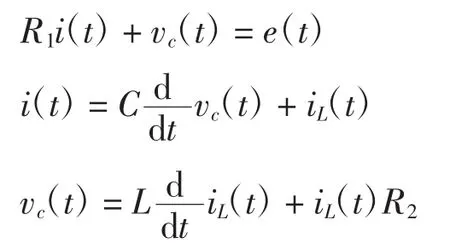
先消去变量vc（t），再消去变量iL（t），将电路参数代入整理得微分方程为：

以此类推，一个k阶的线性系统激励信号与响应信号之间的关系，可以用以下形式的k阶微分方程式来描述：

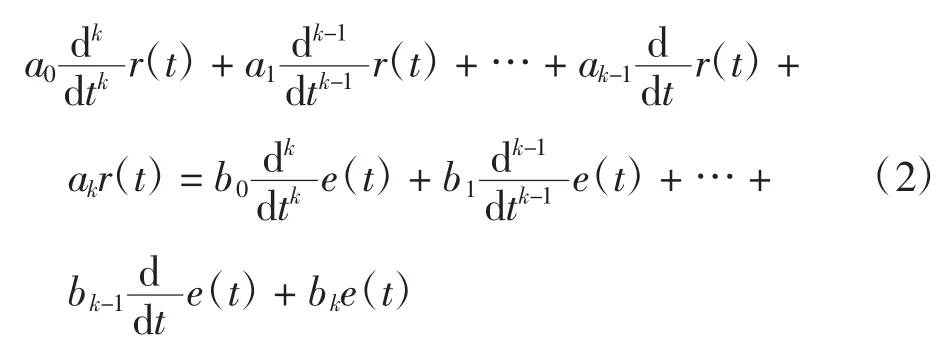
若系统为时不变，则式（2）中的ai、bi均为常数。方程的阶次由系统中独立的动态元件个数决定。

1.2 模拟信号电路系统的系统函数分析

模拟信号系统可以用系统函数进行分析，系统输出与输入的比例关系描述了系统自身的系统函数。式（2）所描述的系统可以用一个矩形方框图简单表示，如图2所示。

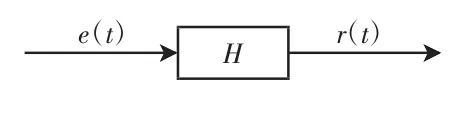
图2 系统方框图

方框图左边的有向线段表示系统的输入e（t），右边表示系统的输出r（t），方框表示联系输入和输出的其他部分，是系统的主体。此外，几个系统的组合连接又可构成一个复杂系统，称为复合系统。系统的组合连接方式有串联、并联及这2种方式的混合连接。连续系统串联时域形式和复频域形式如图3所示。

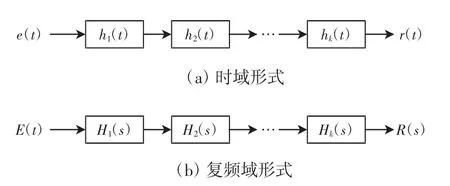
图3 连续系统的串联

设复合系统的冲激响应为h（t），时域线性连续系统h（t）与hi（t）的关系为：

若h（t）和hi（t）为因果函数，h（t）的单边拉普拉斯变换即系统函数为H（s），根据单边拉普拉斯变换的时域卷积性质，H（s）与Hi（s）的关系为：

k阶系统的系统函数为：

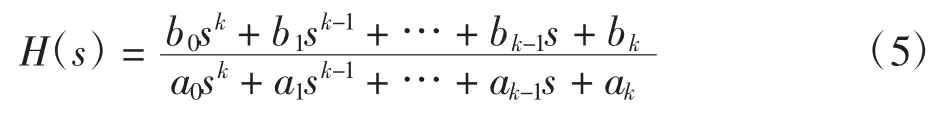
2 系统方框图的建立与分解

在通信工程系统的设计中，对高阶系统进行仿真时，需要求解高阶微分方程，此时变量耦合问题较难处理。利用方框图仿真方法可以解决这个问题，且计算简单、界面直观，对工程系统的设计起到较好的辅助作用。仿真的重要一步是仿真模型的建立。建立仿真模型是通过对所研究事物的相关信息进行提取、抽象和综合之后，在与其对应的信息空间中建立与原事物相似的一种表示或描述[4-5]。方框图仿真模型是由一些能完成最基本运算的功能框图组成。本文主要介绍在已知系统微分方程的情况下，如何获取系统函数并利用系统函数分解的方法实现方框图。

2.1 微分方程到系统函数的转换

假定某一物理系统可用式（2）的微分方程表示，令a0=1，其系统函数如式（5）。为便于系统分析，将式（5）中分子、分母分别提取Sk得到：

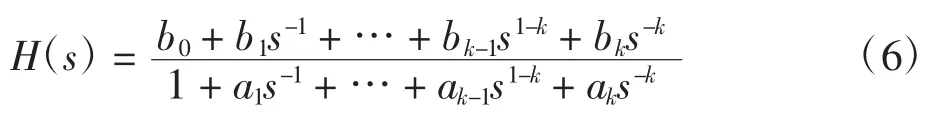
当用积分器1/s来实现该系统时，式（6）的信号流图如图4所示[6-7]。

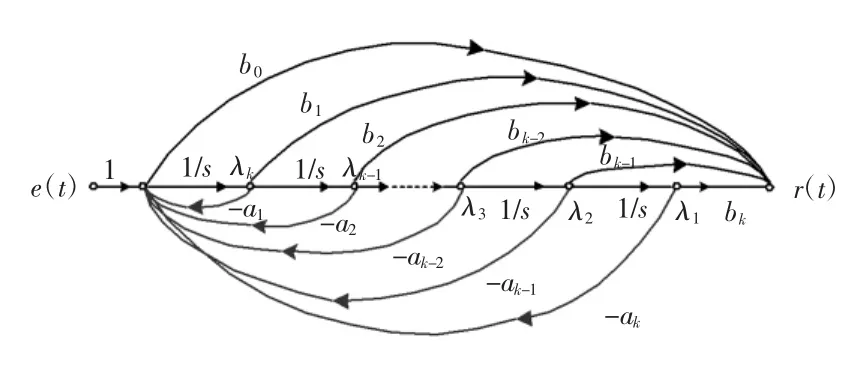
图4 式（6）的信号流图

2.2 系统方框图的分解实现

在计算系统输入输出间的转移函数时，利用梅森公式既简洁又方便。梅森公式为：

式中：Δ为流图的特征行列式，Δ=1-（所有不同环路增益之和）+（每2个互不接触环路增益乘积之和）-（每3个互不接触环路增益乘积之和）+……；k为由源点到阱点之间第k条前向通路的标号；gk为由源点到阱点之间第k条前向通路的增益；Δk为对于第k条前向通路特征行列式的余因子。

根据梅森公式对式（6）的分析，可以看到式（6）的分母正如图4的信号流图所示，构成了梅森公式的k个反馈环，而分子构成了梅森公式的k个前向通道。根据这一特点，这里引入变量H1（s）和H2（s），将式（6）写为：

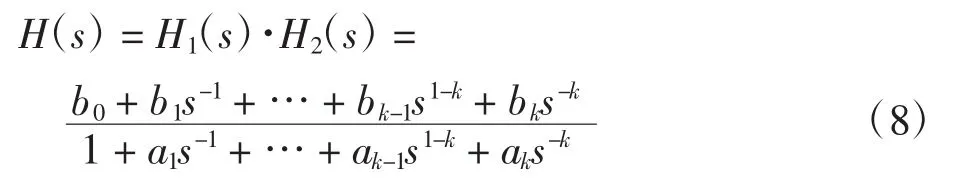
为实现方框图的分解，在式（8）中引入新的变量M（s），由此得到：

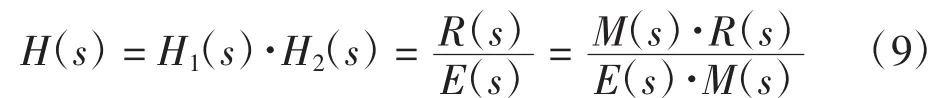
根据式（9），k=2时画出的全系统方框图如图5所示。为实现全系统函数的分解，得到分解后的系统方框图，这里设法将系统函数分解成梅森公式反馈环路和前项通道的形式。由式（9）可得到：

同理：

由式（10）可以得到：

图5 k=2时的系统方框图

在此求出M（s）为：

由式（11）可以得到：

至此完成了对式（8）全系统函数的分解。显然，式（12）为系统反馈环路方框图的形式，式中k=2时的系统方框图如图6所示。式（13）为系统前项通路方框图的形式，式中k=2时的系统方框图如图7所示。

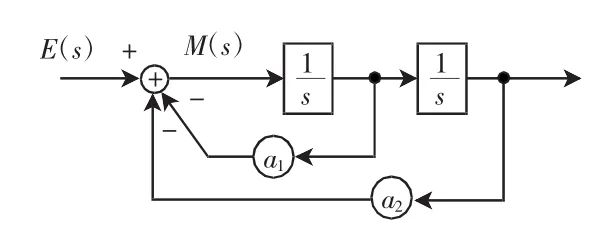
图6 k=2时反馈环路方框图

图7 k=2时前向通路方框图

图6和图7的2个方框图是图5方框图的线性分解，分解后的方框图保留原系统的全部属性，既可以方便用于系统反馈环路的分析，也可以简捷地测试前向通道，必要时可以起到对整个系统进行辅助分析的作用。

3 方框图分解的正确性验证

为证明上述分解的正确性，保持式（2）等号左边的形式不变，将变量r（t）用M（t）代替，并令其等于e（t）的k阶导数，从式（2）中建立方程式为：

之后保持式（2）等号右边的形式不变，将变量e（t）用M（t）代替，并令其等于r（t）的k阶导数，得到方程式为：

对式（14）取拉普拉斯变换得到：

等式两边除以Sk得：

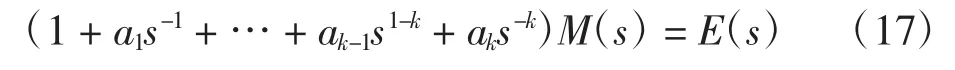
同理，对式（15）取拉普拉斯变换并化简可得：

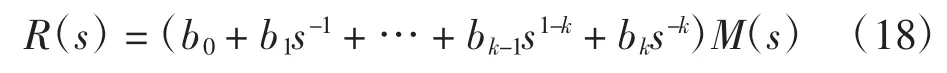
由式（17）和式（18）相除可得到：

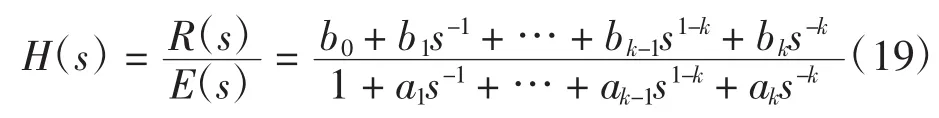
上述式（17）、式（18）和式（19）与前述式（12）、式（13）和式（8）完全相同，至此证明了前述分解的正确性。在该证明过程中，考虑到频域分析时具有零极点对消现象，所以分别在式（14）中设定等式右端为e（t）的k阶导数，式（15）中设定等式左端为r（t）的k阶导数。若不考虑零极点对消现象，直接设定为e（t）和r（t）即可根据时域微分方程画出时域方框图。由于许多文献对此都有讨论，这里不再赘述。

4 结束语

方框图仿真模型由一些能完成最基本运算的功能框组成，是描述被仿真系统的功能、组成、连接、参数及输入和输出关系的信息传递图。方框图仿真是以系统的方框图作为仿真模型，进行程序设计、求解和分析。利用方框图方法建立基于MATLAB/Simulink的模型，可方便得出正确的分析结果[8-9]。本文正是基于方框图法在系统功能分析中具有的重要作用而展开探讨，将复频域方框图进行分解是对方框图分析方法进行研究的尝试，为通信工程系统应用分析提供辅助的参考方法，为感兴趣的研究者提供帮助。

［1］ 杜小坤，李国徽，李艳红.模式匹配中的结构差异识别及消解［J］.计算机科学，2015，42（2）：185-190.

［2］ CARVALHO M S G，LEANDER A H F，GONALVES M A，et al.An evolutionary approach to complex schema matching［J］.Information Systems，2013，38（3）：302-316.

［3］ 郑君里，应启衍，杨为理.信号与系统［M］.3版.北京：高等教育出版社，2013.

［4］ 张新燕.面向方框图仿真的模型建立与仿真计算［J］.计算机工程与设计，2005，23（9）：41-44.

［5］ 范艳根，王玉萍，汤旭日.系统微分方程与系统框图互换的两种方法［J］.黑龙江科技学院学报，2005（1）：47-49.

［6］ 王智文.几种边缘检测算子的性能比较研究［J］.制造业自动化，2012，6（34）：14-17.

［7］ 雷天翔.解析法化简控制系统传递函数方框图的研究［J］.河北工业科学，2012，2（5）：295-298.

［8］ 郭湘军，吴尧，吴书新.MATLAB在电子信息专业课程教学中的主要应用［J］.电子技术与软件工程，2014，6（4）：53-56.

［9］ 张铮，倪红霞，苑春苗，等.精通Matlab数字图像处理与识别［M］.北京：人民邮电出版社，2013.

Study of building models and charts for linear time invariant system

ZHANG Ze-hao1，JI Wu-sheng2
（1.Tianjin Zhonghuan System Engineering Co.，Ltd，Tianjin 300060，China；2.School of Electronic and Engineering，Tianjin University of Technology and Education，Tianjin 300222，China）

A kind of method of drawing a system chart is introduced in this paper，by using the operator to transforming differential equation into a system function and by using Mason formula to decompose the system function.The method can be applied to the analysis of communication engineering system，and it plays an auxiliary role in the whole analysis.By using the decomposition of the block diagram of the system，the forward channel and the feedback loop are discussed respectively，which can simplify the direct analysis of complex systems，and reduce the difficulty of system analysis to a certain extent. The method is proved by mathematical analysis.

linear time invariant system；differential equation；system chart

O224

A

2095－0926（2016）04－0032－04

2016-10-13

张赜皓（1987—），男，助理工程师，研究方向为通信系统工程；姬五胜（1968—），男，教授，博士，硕士生导师，研究方向为信息与通信工程、电磁场与微波技术.