基于边界积分法的V型切口尖端应力场分析
2017-01-10刘剑,戴怡
刘 剑,戴 怡
(天津职业技术师范大学数控技术与可靠性研究所,天津 300222)
基于边界积分法的V型切口尖端应力场分析
刘 剑,戴 怡
(天津职业技术师范大学数控技术与可靠性研究所,天津 300222)
针对大静载荷作用下V型切口尖端附近应力的相关问题,在断裂力学已有成果的基础上,推导了格林函数边界单元法的基本理论及计算公式,通过采用边界积分单元的方法,编写和调试MATLAB程序,计算所有积分方程的解,得出V型切口边界的应力值和较大应力值的位置。
应力;边界积分;断裂;V型切口
由于现实中的裂纹一般是三维的,传统断裂力学中“裂纹是平直”的假设不再成立,因此在三维结构中裂纹沿曲线或曲折路径扩展成为一个棘手的力学难题。目前针对这一问题的研究多从实验方面展开,唯象的经验性结果占据多数,且以平面裂纹为主[1]。近几十年来,计算机技术的发展为数值模拟奠定了基础,有限元等计算力学方法的提出和发展也为采用数值方法解决这一难题提供了条件。
虽然有限元对弹塑性问题的分析为应力应变场的分析提供了依据,但对于三维复杂结构的应力分析,在采用有限元法求解时,应力集中区需要划分比较密集的网格,使未知量数目增加、总体刚度矩阵带宽变大,给求解带来困难。此外,有限元往往是通过位移近似值来计算应力,得到的边界应力结果一般较差,而应力集中又正好发生在边界上,用有限元求解这类切口问题显然不合适。边界元法采取边界上积分的形式,降低了问题的空间维数,将三维问题转变为二维,从而大量减少了未知量的数目。此外,边界元法以边界上的量为控制对象,因而可直接得到边界上的应力值。因此,边界元法比有限元法更适合于求解这类应力集中问题[2-3]。本文采用边界积分的方法求解平面V型切口的应力场,得到V型切口边界的应力值和较大应力值的位置。
1 格林函数法边界积分方程
1.1 边界积分方程
平面V型切口如图1所示。一般而言,在求解平面问题时要结合边界条件求解平衡微分方程。对于常体力平面问题的计算,在直角坐标下的平衡微分方程为[4-5]:

为使计算方便,将应力Airyφ(x,y)表示为:
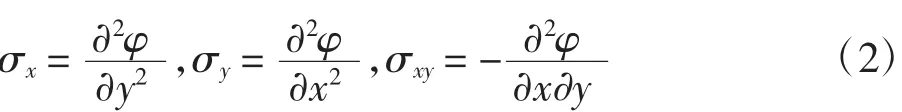
式中:φ(x,y)为应力函数;σx、σy、σxy为某一点处的应力分量。
在平面应力的计算过程中,必须满足边界条件,这是计算成立的基础。边界平面如图1所示,所有平面边界条件可表示为(其中q为载荷):

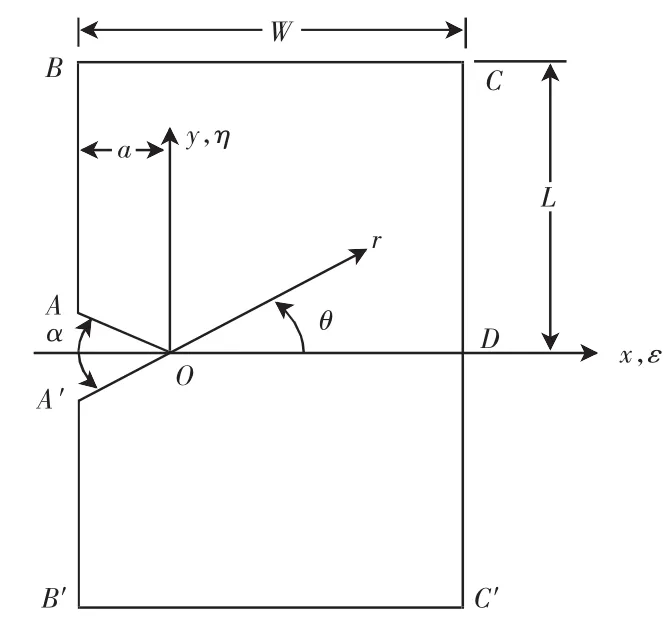
图1 平面V型切口
采用格林函数第二方程时,方程要满足边界条件式(3)。单连通区域R,其边界分为光滑曲线C、线积分方向与外法线正向,如图2所示。

图2 单连通区域R上的符号规定
由文献可知,格林第二方程可表示为[6](其中U、V为2个函数,n为外法线):

令

将式(5)代入式(4)得:
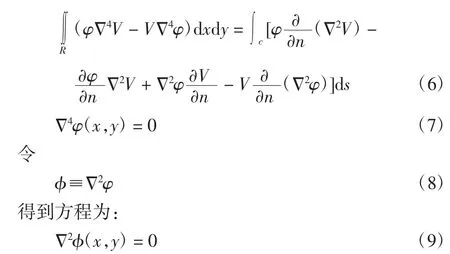
由图2可知,令r(x,y;ε,η)为区域R上任意2点p(x,y)和q(ε,η)之间的距离,p为节点的坐标值,q为起始点的坐标。将式(5)、式(8)和式(9)代入格林方程。令V=ln r,并考虑r=0的奇异性,得到[7]:
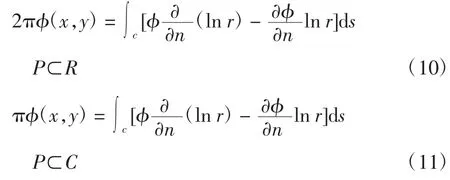
将式(5)和式(7)与(8)联立,取V≡P=ln r,考虑在r=0点的奇异性,得到:

1.2 V型切口的应力方程
为方便计算,以下用撇号“′”代表法相导数。将边界C分成n段(即n个单元)如图3所示。在每一单元上取φ和φ′为恒定值,每一单元的中点为节点,φi和φi′即为该点上的值。

图3 边界C上的单元化分
由于应力函数φ在边界BC和B’C’上并不是常数,所以φ逐段为常数的假设必然导致较大误差。为克服这种困难,在加载边BC和B’C’上使用直接积分取代φ[8-10]。
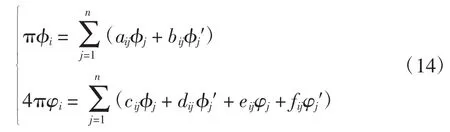
当i=1,2,3,…,n时,通过式(14)得到:

式中:rij为第i个节点到任意节点j的距离;ρij=(r2lnr)ij。当i≠j时,式(15)的系数可以采用Simpson法求出;当i=j时,式(15)的系数可以采用解析法求出。当边界全部由直线组成时,采用解析法求出系数矩阵。式(14)可以用矩阵方程表示为[11-12]:

即归结为:

式中:A为2n×2n阶矩阵;X和R为2n×1阶列矩阵。
矩阵A由平面板的几何尺寸和边界单元数目的分布共同确定。矩阵R依赖于应力场,即依赖于矩阵X。为通过式(12)求得应力,可不对应力函数进行微分,而直接在积分符号下进行微分;且当边界上φ和φ′均为已知时,采用式(16)通过同样形式的积分就可以求得所需应力。
将式(2)、式(12)和式(14)联立求得应力方程为:

2 平面应力计算
为使计算简便,在计算应力的过程中将应力函数、载荷及坐标均进行了无量纲化处理。使用MATLAB对平面V型切口进行划分,如图4所示。

图4 V型切口下边界单元的划分
由于是计算边界节点的应力值,每个节点的应力值依次分为σx、σy、σxy进行计算。节点划分使用平均划分的办法,在平面上沿边界CD取边界单元数序号为1~5,AB边取单元数序号为6~10,OA边取边界单元数序号为11~15,BC边取边界单元数序号为16~20,分别对应图4中节点的位置。通过边界积分算法对所取的20个边界单元进行应力计算,求得式(18)的解,计算结果如图5至图7所示[13-16]。
从图5至图7能够得到20个边界单元的应力值,且在3幅图中都有一点的应力值正好为V型切口处的应力值,说明V型切口处的应力集中较大;而一般断裂也往往发生在V型切口处,所以裂纹的危害较大。因此,研究V型切口的应力值具有实际意义,也为求取边界应力提供了一种有效的方法。

图5 σx的应力值
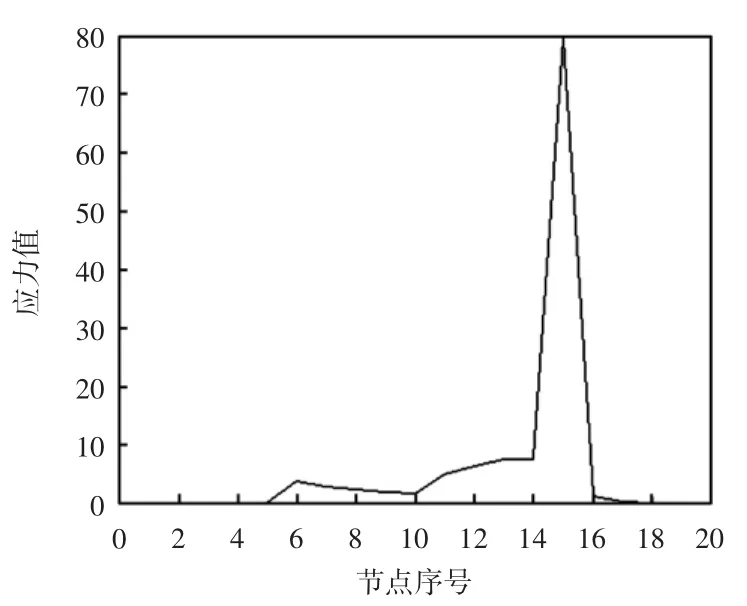
图6 σy的应力值

图7 σxy的应力值
3 结束语
本文利用边界积分的方法对平面V型切口进行应力计算,这种方法将二维积分问题转化为一维积分问题,是一种与有限元法并列的求取应力的方法。该方法直接计算边界上的应力值,原理直观简明;缺点是计算难度增大,会遇到病态矩阵,依赖计算方法的突破。当计算方法及计算手段改进时,计算结果将得到改进。随着智能计算及大数据理论的不断发展,边界积分方法也将获得进一步的完善。
[1] 魏庆同,郎福元.机械加工中断裂设计概念[J].甘肃工业大学学报,1982(1):1-19.
[2] 魏庆同,郎福元,赵邦戟.V型切口尖端力场和位移场的幂级数解[J].甘肃工业大学学报,1985,11(2):10-14.
[3] 赵邦戟,魏庆同,郎福元.三点弯曲梁的应力强度因子K1[J].甘肃工业大学学报,1985,11(4):28-32.
[4] 魏庆同,郎福元,赵邦戟.I型裂纹的扩展方向及其稳定性[J].甘肃工业大学学报,1986,12(3):51-55.
[5] 南京工学院数学教研组.数学物理方程与特殊函数[M].北京:人民教育出版社,1978.
[6] 王元淳.边界元法基础[M].上海:上海交通大学出版社,1988.
[7] 葛仁余.弹性和塑性V形切口应力奇异性分析与界面强度的扩展边界元法研究[D].合肥:合肥工业大学,2014.
[8] 魏庆同,郎福元,赵邦戟.一种求解V型切口尖端应力强度因子K1的新方法[J].甘肃工业大学学报,1986,12(4):21-31.
[9] MENDELSON A.Boundary-Integral Methods in Elasticity and Plasticity[Z].NASA TN-D-7418,1973.
[10]钱文杰,王纬波,田常录.一种V型切口应力强度因子的计算公式[J].机械制造与自动化,2016(4):21-23.
[11] 曹志浩,张玉德,李瑞遐.矩阵计算与方程求根[M].北京:高等教育出版社,1986.
[12] 邓勇.矩阵的满秩分解及应用[J].喀什师范学院学报,2015(6):1-3.
[13]刘浩,韩晶.MATLABR2014a完全自学一本通[M].北京:电子工业出版社,2015.
[14]赵海滨.MATLAB应用大全[M].北京:清华大学出版社,2012.
[15]程小红.基于MATLAB图像简单处理应用[J].电脑知识与技术,2013(15):3613-3616.
[16] 聂影.MATLAB软件应用研究[J].软件导刊,2014(7):102-104.
Based on boundary integral method of V-shaped notch tip stress field analysis
LIU Jian,DAI Yi
(Laboratory of Reliability Engineering and Numerical Control Technology,Tianjin University of Technology and Education,Tianjin 300222,China)
As to the problem of the stress near the tip of the V-shaped notch under the action of large static load,on the basis of the results of fracture mechanics,the basic theory and calculation formula of the Green function of the boundary element method are deduced.By using the method of boundary integral unit,compiling and debugging MATLAB procedures,all solutions of the integral equation are calculated and the V cut boundary stress value and the stress of the position are obtained.
stress;boundary integral;fracture;V-shaped incision
TH114
A
2095-0926(2016)04-0036-04
2016-06-23
天津市学科领军人才培养计划(RC14-02);天津职业技术师范大学科研发展基金项目(KJY12-13).
刘 剑(1990—),男,硕士研究生;戴 怡(1962—),男,教授,博士,硕士生导师,研究方向为机电设备可靠性工程.
