数学问题解答

2017年8月号问题解答

（解答由问题提供人给出）

2376某委员会开了40次会议，每次有10人出席，而且委员会任两个成员都未在一起出席过一次以上的会议，证明：该委员会成员一定至少有82人.

（浙江省富阳市第二中学 许康华 311400；浙江省富阳市永兴中学 段春炳 311400）

证明设该委员会有n成员，用n个顶点u1，u2，…，un表示这n个成员，用40个顶点v1，v2，…，v40表示40次会议，如果成员ui出席会议vj则在顶点ui与顶点vj之间连一条边，否则，在其他两顶点之间都不连边，这样得到一个二部图G，则图G的顶点集为U∪V，其中U=｛u1，u2，…，un｝，V=｛v1，v2，…，v40｝，边数为400.因此有.

对于任意的顶点ui∈U，与ui相邻的顶点对有个.由于任两个成员都未在一起参加过两次不同的会议，所以图G中没有四边形，因此，当ui在U中变化时，所有的顶点对都是互不相同的，否则，点对分别在中被计算，那么ui，vk，uj，vl就组成一个四边形.所以

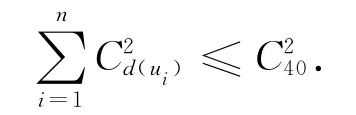
由柯西不等式，有

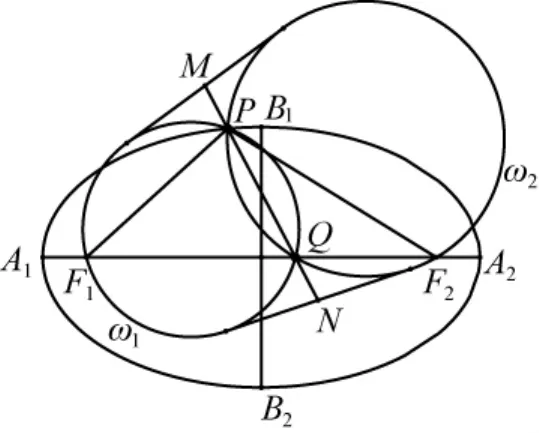
23 77 设椭圆的长轴为A1A2，短轴为B1B2，焦点为F1和F2，P为椭圆上异于其顶点的任意一点，Q为线段F1F2上异于其端点的任意一点，ω1，ω2分别为△F1PQ和△F2PQ的外接圆，M，N分别为直线PQ与ω1，ω2的两条外公切线的交点，求证：.

（河南省辉县市一中 贺基军 453600）

证明如图1，设两圆ω1，ω2的圆心分别为O1，O2，两圆的公共弦PQ与直线O1O2的交点为R，点M所在的外公切线与两圆ω1，ω2的切点分别为M1，M2.

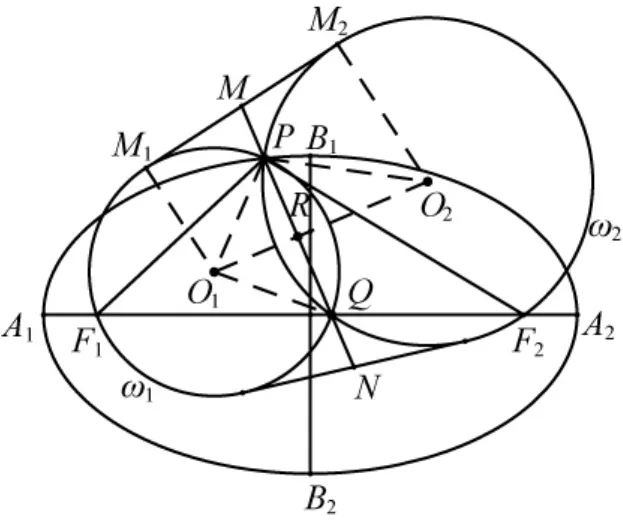
图1

根据对称性可知，直线O1O2同时为线段PQ和线段MN的垂直平分线，其垂足为R.

故MM1=MM2，M为线段M1M2的中点.

连接PO1，PO2和QO1.

又同理得 ∠PO2O1=∠PF2F1，

故△PO1O2∽△PF1F2，

因点P异于椭圆的顶点，故PF1≠PF2，这里不妨假设PF1＜PF2，从而有PO1＜PO2，即圆ω1的半径小于圆ω2的半径.

连接O1M1，O2M2，则O1M1⊥M1M2，O2M2⊥M1M2，四边形M1O1O2M2为直角梯形.作该梯形的高O1H及中位线MK，如图2所示.

图2

因O1H⊥M2O2，O1O2⊥MR，

又MK∥M2O2，∠O1O2H=∠MKR，

故R t△O1O2H∽Rt△MKR，

因O1H=M1M2，2MR=MN，

根据椭圆的定义及性质得

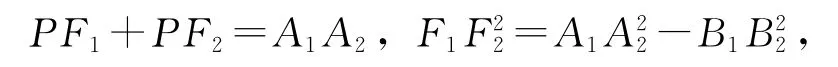
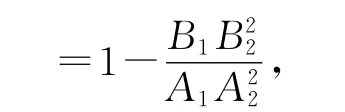
另一方面，注意到

2378设正实数x1，x2，…，xn满足x1+x2+…+xn=s，且p≥1，求证：

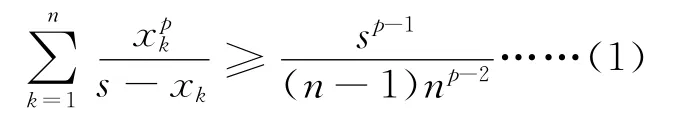
（天津水运高级技工学校 黄兆麟 300456）

证明由幂平均不等式，当p≥1时有

由不等式（1）的全对称性，不失一般性，可设

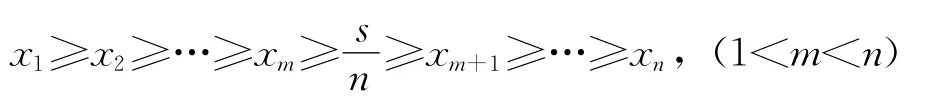
又设不等式（1）左右之差为M且左右平均分配作差，那么可得

至此，表达式M中共有n个差项，且前m个差项分子均非负且递减，后n-m个差项分子均非正且递减，虽然又有非负项又有非正项，但它们可同向放缩！即有

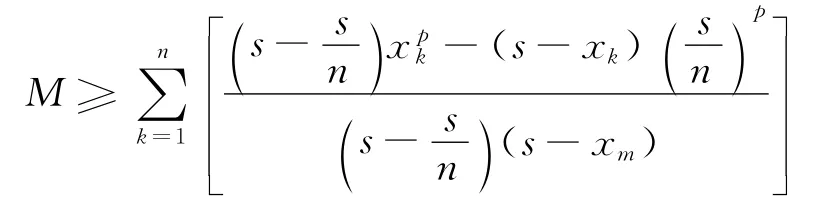
（注意此时分母中s-xm为常量）

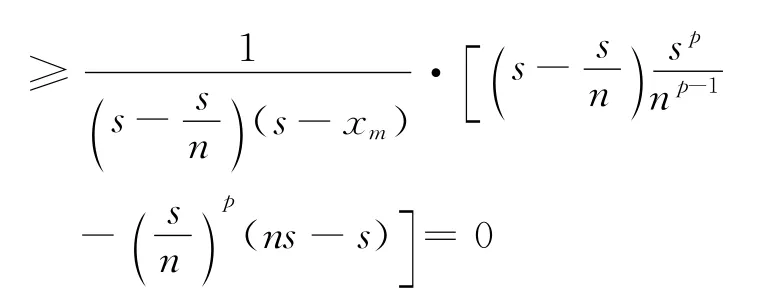
故不等式（1）成立.

2379 如图，在四边形ABCD中，DA、CB分别和圆O相切，切点A、B，AC交BD于H，F、E分别为DA、CB中点，当FE切圆O于G时，求证：GH延长线平分AB.

（江西师范高等专科学校 王建荣 335000；温州私立第一实验学校 刘沙西 325000）

证明设GH延长线交AB于I；BD、AC分别交EF于M、N，连接AG、BG分别交BD、AC于K、R，由梅涅劳斯定理：

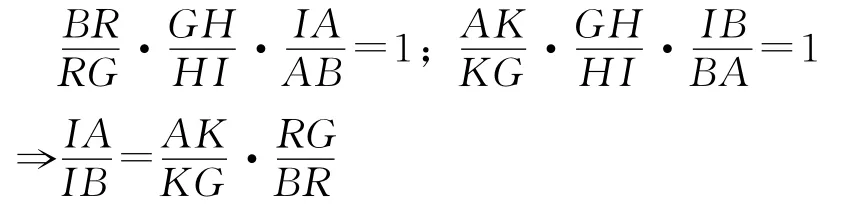
同理

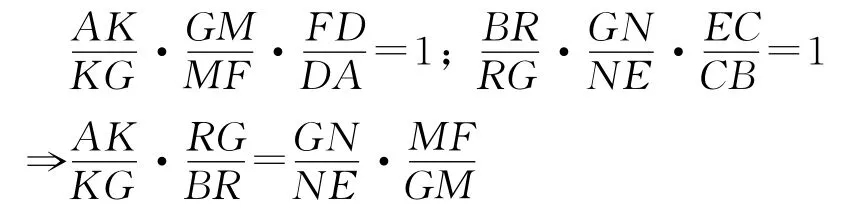
同理

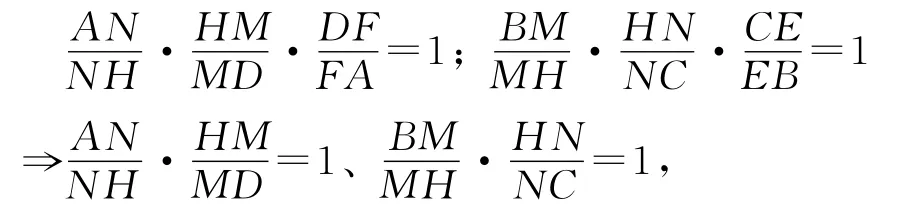
由∠DAB=∠CBA，

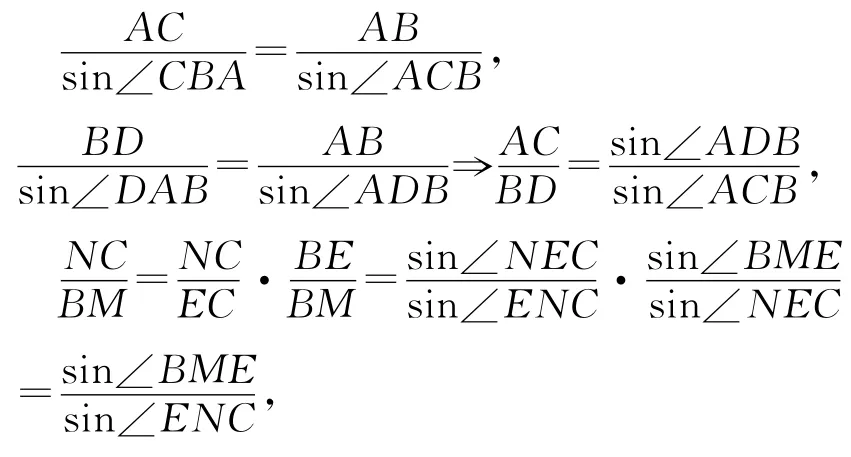
由AF=FG=DF，BE=EG=E C，

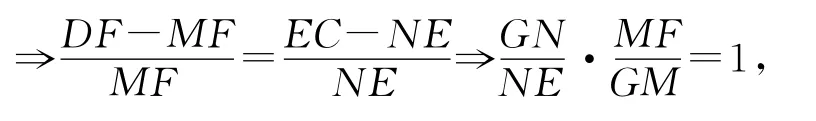
故GH延长线平分AB.

2380在△ABC中，M是边BC上任意一点，若△ABC、△ABM与△ACM的内切圆半径分别为，求证：为定值.

（浙江省慈溪市慈溪实验中学 华漫天 315300）

证明如图，设I、I1、I2分别为△ABC、△ABM、△ACM的内心，点F为△ABC的内切圆在边BC上的切点，作I1P⊥BC于P，I2Q⊥BC于Q，连结F I1、F I2、I1I2、I1M、I2M，

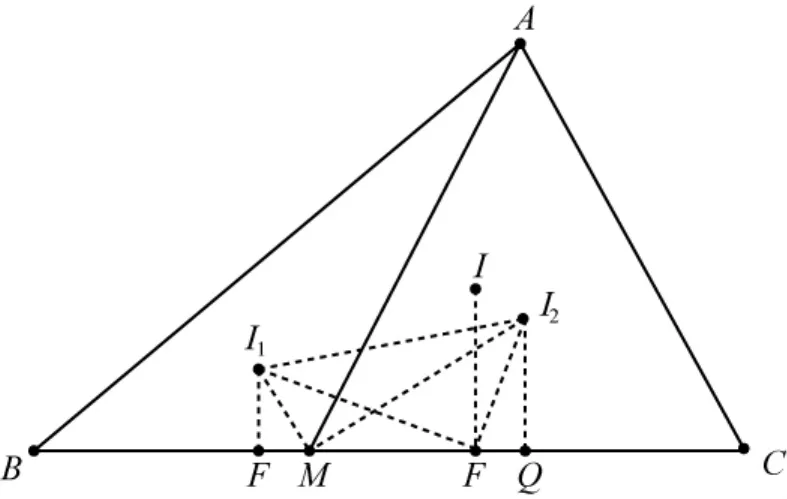
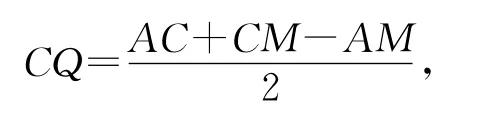
所以PF=MQ，

易知△PI1M∽△QM I2，

又由∠I1PF=∠FQI2=90°，

故△PI1F∽△QFI2，

设a、b、c为△ABC三边长，s表示△ABC的半周长，

相乘得

2017年9月号问题

（来稿请注明出处——编者）

2381设△ABC的三边长，对应边上的中线长，角平分线长，高线长，半周长，外接圆及内切圆半径分别为a，b，c，ma，mb，mc，wa，wb，wc，ha，hb，hc，s，R，r，

（天津水运高级技工学校 黄兆麟 300456）

2382如图，在△ABC中，AB=BC，D是AB延长线上的一点，E是BC延长上的一点，且CE=AD.延长AC交DE于F，FG∥BE交CD于G，FH∥AD交AE于H.

求证：（1）FG=FH；（2）A F⊥GH.

（濮阳职业技术学院 纪保存 457000）

2383n是大于3的奇数，证明：n！+1与（n！-n）！+1中至少有一个是合数.

（浙江温州市区马鞍池东路1-408 陈克瀛 325000）

2384设a，b，c分别表示△ABC三内角A，B，C所对的边长，求证：

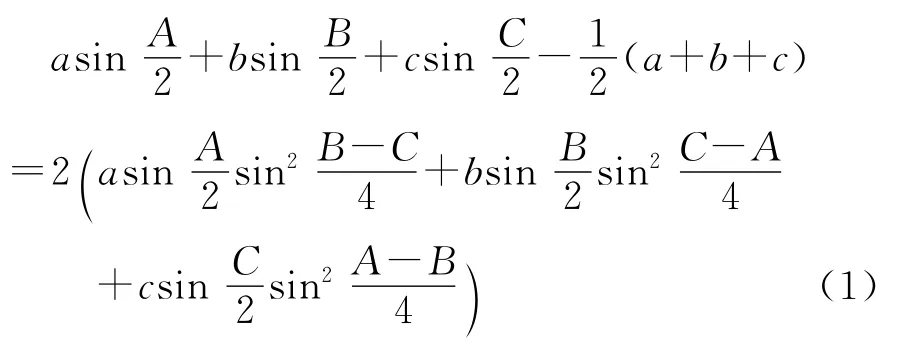
（河南质量工程职业学院 李永利 467000）

2385如图，⊙O与⊙O1内切于点A，⊙O与⊙O2内切于点B，且⊙O1与⊙O2相交于点C、D，AB交CD于点T.求证：S△TOO1=S△TOO2.

（重庆市合川太和中学 袁安全 401555）