Ⅲ型轨枕有砟轨道动刚度特性研究

亓伟，李成辉，郑建，刘玉涛

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031)

Ⅲ型轨枕有砟轨道动刚度特性研究

亓伟，李成辉，郑建，刘玉涛

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031)

轨道动刚度是反映轨道动力特性的重要参数。本文通过建立Ⅲ型轨枕有轨道力学模型，研究扣件刚度、扣件阻尼、道床刚度等轨道结构参数的变化与轨道动刚度的关系。结果表明:增加扣件刚度会增大轨道第1反共振频率、第2共振频率及轨道动刚度的波动幅值，会增加低频范围内的轨道动刚度，而降低中、高频范围内的轨道动刚度;增大扣件阻尼会削减轨道动刚度的波动幅值，当扣件阻尼为75 kN·m/s时，在中、高频范围内，轨道动刚度波动幅值很大程度上会被削减;道床刚度的增大使得轨道第1共振频率、第1反共振频率增大，轨道动刚度波动幅值减小;通过降低扣件刚度、增加扣件阻尼、增加道床刚度等措施可以有效减小轨道共振，从而实现有砟轨道的动平顺性。

高速铁路;有砟轨道;动刚度;轨道参数;激振频率

高速铁路有砟轨道是由60 kg/m的钢轨、弹条Ⅴ型扣件、Ⅲ型轨枕、有砟道床等轨道结构组成的复杂系统。在列车荷载长时间作用下，扣件、道床等结构的力学性能会发生较大变化。有砟轨道动刚度是轨道各结构动力响应的叠加，而结构参数的变化会影响轨道动刚度，对轨道动平顺性产生影响，故需要研究有砟轨道结构参数与轨道动刚度的关系。

由于影响轨道特性的参数数量较多，因此，在研究过程中，为研究某一参数对轨道系统的影响，首先假定其余参数一定，通过改变所研究的参数得到轨道的响应，再根据轨道响应-影响参数的关系曲线得到最佳的参数选取范围［1］。目前对轨道参数的研究包括轨道动力性能、轨道减振降噪、轮轨关系等。文献［1-5］分析了改变扣件垂向刚度、横向刚度、垂向阻尼，道床垂向刚度、横向刚度、垂向阻尼，以及轨枕质量、道床板、轨道板厚度等参数对轨道动、静力学性能的影响。文献［6-10］讨论了浮置板式轨道在地铁减振降噪方面的应用。文献［11-14］主要对轮轨关系及轮轨磨耗进行了分析，得到了合理的轨道参数设置范围。

本文基于有砟轨道力学模型，探讨了扣件刚度、扣件阻尼、道床刚度等参数对轨道动刚度的影响，为削弱轨道动刚度波动，实现线路动平顺提供理论依据。

1 力学模型

本文依据Ⅲ型轨枕有砟轨道建立力学模型，如图1所示。建模时钢轨与Ⅲ型轨枕只考虑在列车作用下产生的竖向力及竖向挠曲，模型中将钢轨、轨枕简化为铁木辛柯梁;扣件与有砟道床在竖向力分析中只起支承、传力的作用，故简化为竖向弹簧与阻尼器。为消除边界效应，取轨道长度为50根轨枕长度。轨道垂向动刚度主要与列车垂向荷载有关，故模型中仅考虑轨道结构在垂向稳态激励作用下的响应。为分析不同频率荷载作用下有砟轨道的响应，在钢轨中央位置作用F=F0eiωt的竖向荷载，其中F0为列车静轴重，i为虚数，ω激振频率，t为时间。高速列车轴重集中在14～17 t，故本文选取轴重15 t进行分析。激振频率则选取涵盖低、中、高频的1～4 000 Hz进行研究。

轨道结构的刚度、阻尼是在一定范围内波动的，一方面是由于列车循环荷载作用，导致结构发生变形、老化，另一方面是根据线路要求对轨道结构的设置不同导致的。本文根据文献［15-18］确定相应的轨道结构参数。目前高速铁路常用扣件刚度范围为30～100 kN/mm，本文选取扣件刚度30，60，100 kN/mm，扣件阻尼3，15，75 kN·m/s进行分析。

有砟道床在累积沉降作用下或在道砟胶等材料粘结后刚度会增加，但是阻尼改变量较小。高速铁路有砟道床规范规定道床刚度＞70 kN/mm，而常用道床刚度为120 kN/mm，应用道砟胶后道床刚度会增加更多，故本文分别选取道床刚度70，120，200 kN/mm，道床阻尼60 kN·m/s进行分析。

本文以扣件刚度60 kN/mm、扣件阻尼15 kN·m/s、道床刚度120 kN/mm、Ⅲ型轨枕为基本有砟轨道结构参数，在此基础上，通过改变单一轨道结构参数，研究不同轨道结构参数对轨道动刚度的影响。

2 结构参数对轨道动刚度的影响

2.1 扣件刚度

有砟轨道动刚度见图2，由图可知:在1～50 Hz，轨道动刚度受荷载激振频率的影响较小。因此在对数坐标系里，为更好地显示轨道动刚度的变化，之后轨道动刚度图的频率起点改为10 Hz。在50～115 Hz，随着激振频率的增加，轨道动刚度大幅度减小，在115 Hz时轨道动刚度达到最小值(轨道的第1共振频率)。在115～163 Hz，随着激振频率的增加，轨道动刚度逐渐增加，并在163 Hz时轨道动刚度达到极大值(轨道第1反共振频率)。在163～234 Hz，轨道动刚度随激振频率的增加逐渐减小，在234 Hz时达到极小值(轨道第2共振频率)。因为建立的轨道只包含钢轨、轨枕2层结构，故在动刚度图中仅出现2个明显的共振频率点。

当激振频率高于234 Hz后，随着激振频率的增加，轨道动刚度逐渐增加(1 600 Hz频段为轨道的pined-pined频率［19］，是系统固有属性，本文不考虑)。由此可知，为实现线路平顺性，需要控制共振频率和反共振频率范围内的轨道动刚度波动幅值。

扣件刚度与轨道动刚度的关系曲线见图3，由图可知:在10～50 Hz，随着扣件刚度的增加，轨道动刚度逐渐增大。在50～115 Hz，由扣件刚度差异造成的轨道动刚度间的差异随频率的增加而逐渐减小，在115 Hz时轨道动刚度差异最小。扣件刚度的增加使得轨道动刚度的第1反共振频率、第2共振频率增大，动刚度波动幅值增加。当激振频率高于第2共振频率后，扣件刚度越大轨道刚度越小，随着激振频率的增加，扣件刚度的影响逐渐减小。

图3 扣件刚度与轨道动刚度的关系曲线

扣件刚度对轨道刚度比的影响见图4，由图可知:扣件刚度的改变会影响全频范围内的轨道动刚度，对低于300 Hz的中、低频的轨道动刚度影响较大，轨道动刚度的改变超过原来动刚度的25%。在中、高频段内，扣件刚度对轨道动刚度的影响随着激振频率的增大，刚度比逐渐趋于1，即扣件刚度对高频段的轨道动刚度影响变小。

图4 扣件刚度对轨道刚度比的影响

2.2 扣件阻尼

在动力学的分析中，阻尼的作用是使系统振动衰减。在轨道各结构中，由于扣件中的轨下胶垫由橡胶材料制成，可通过改变材料属性改变扣件阻尼，因此本文仅分析扣件阻尼改变对轨道动刚度的影响。扣件阻尼与轨道动刚度的关系曲线见图5。

图5 扣件阻尼与轨道动刚度的关系曲线

由图可知:在10～50 Hz，扣件阻尼对轨道动刚度的影响很小。在50～115 Hz，扣件阻尼的增加使得轨道动刚度减小幅度降低，扣件阻尼在75 kN·m/s时的轨道动刚度最大。在激振频率高于115 Hz后，扣件阻尼的增加使得轨道动刚度波动幅值显著下降，减振效果明显。

扣件刚度对轨道刚度比的影响见图6，由图可知:扣件阻尼在荷载激振频率低于50 Hz时对轨道动刚度的改变量＜5%，随着激振频率的增加，扣件阻尼对轨道动刚度的影响逐渐增大。在第1共振频率范围内，扣件阻尼为3 kN·m/s时，轨道动刚度的改变量＞25%;扣件阻尼为75 kN·m/s时，轨道动刚度的改变量＞90%。在第1反共振频率范围内，扣件阻尼为3 kN·m/s时，轨道动刚度的改变量＞35%;扣件阻尼为75 kN·m/s时，轨道动刚度的改变量＞95%。在第2共振频率范围内，扣件阻尼为3 kN·m/s时，轨道动刚度的改变量＞60%;扣件阻尼为75 kN·m/s时，轨道动刚度的改变量＞180%。由此可知，通过增加扣件阻尼可以显著降低频率高于第1反共振频率的轨道动刚度波动。

图6 扣件阻尼对轨道刚度比的影响

2.3 道床刚度

有砟道床是由道砟颗粒组成的，新建铁路与长时间运营线路的道床刚度差异较大。此外，在某些特殊地段对道床采取加固措施后道床刚度增幅较大。道床刚度与轨道动刚度的关系曲线见图7，由图可知:道床刚度的改变仅对10～300 Hz的轨道动刚度影响较大，在10～50 Hz，随着道床刚度的增加，轨道动刚度逐渐增大。在50～300 Hz，随着道床刚度的增加，轨道第1共振频率、第1反共振频率相应增大，在第1共振频率下的轨道动刚度有所增加，在第1反共振频率下的轨道动刚度有所降低，第2共振频率后的轨道动刚度受道床刚度的影响很小。

图7 道床刚度与轨道动刚度的关系曲线

道床刚度对轨道刚度比的影响见图8，由图可知:在10～50 Hz，轨道动刚度幅值的改变量＞10%。轨道处于第1共振频率，且道床刚度为70 kN/mm时，轨道动刚度减小了28%(波动幅值增大);道床刚度为200 kN/mm时，轨道动刚度增大了53%(波动幅值减小)。轨道处于第1反共振频率，且道床刚度为70 kN/mm时，轨道动刚度增大了10%;道床刚度为200 kN/mm时，轨道动刚度减小了9%。道床刚度的改变对于激振频率高于第2共振频率的轨道动刚度影响很小(＜5%)。由此可知，可以通过改变道床刚度对低于300 Hz的轨道动刚度进行调节。

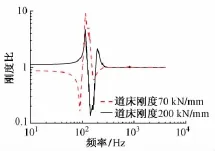
图8 道床刚度对轨道刚度比的影响

3 结论

1)随着扣件刚度的增加，轨道第1反共振频率、第2共振频率以及轨道动刚度波动幅值会增大，增大扣件刚度会增加低频范围内的轨道动刚度，而减小中、高频范围内的轨道动刚度。

2)随着扣件阻尼的增大，轨道动刚度的波动幅值被削减程度相应增大，当扣件阻尼为75 kN·m/s时，轨道动刚度在高于第1反共振频率的中、高频范围内波峰被大幅度削减，轨道动刚度随激振频率增加呈指数增长。

3)轨道第1共振频率、第1反共振频率随道床刚度的增大相应增大，动刚度波动幅值逐渐减小。道床刚度的改变对高于300 Hz的轨道动刚度无影响。

4)轨道各结构参数发生变化后会不同程度的影响轨道动刚度，通过降低扣件刚度、增加扣件阻尼、增加道床刚度可以降低轨道动刚度的波动幅值，实现线路的动平顺性，进而降低轮轨振动，减少轨道病害。

本文仅理论分析了部分轨道结构参数对轨道动刚度的影响，今后需通过相关试验对轨道动刚度作进一步研究。

［1］赵国堂．铁路轨道刚度的确定方法［J］．中国铁道科学，2005，26(1):1-6．

［2］魏伟．轨道参数对轨道系统导纳特性的影响［J］．大连铁道学院学报，1999，20(4):20-25．

［3］ZHAI W，WANG K，CAI C．Fundamentals of Vehicle-track Coupled Dynamics［J］．Vehicle System Dynamics，2009，47 (11):1349-1376．

［4］雷晓燕．轨道过渡段刚度突变对轨道振动的影响［J］．中国铁道科学，2006，27(5):42-45．

［5］GRASSIE S L．Benchmark Test for Model of Railway Track and of Vehicle-track Interaction at Relative High Frequencies［J］．Vehicle System Dynamics，1995，24(S1):355-362．

［6］贾嘉陵，李晓霖．地铁列车不同轨道参数的减振效果分析［J］．中国安全科学学报，2003，13(11):66-72．

［7］李增光，吴天行．浮置板轨道参数激励振动研究［J］．振动与冲击，2010，29(2):17-20，30．

［8］丁德云，刘维宁，李克飞，等．钢弹簧浮置板轨道参数研究［J］．中国铁道科学，2011，32(1):30-35．

［9］曹文战，李芾，丁军君．轨道参数对机车车轮磨耗影响的研究［J］．机车电传动，2015(4):13-17．

［10］POMBO J，AMBROSIO J，PEREIRA M，et al．A Study on Wear Evaluation of Railway Wheels Based on Multibody Dynamics andWearComputation［J］．MultibodySystem Dynamics，2010，24(3):347-366．

［11］王文健，郭俊，刘启跃．轨道参数对轮轨滚动接触行为的影响［J］．四川大学学报(工程科学版)，2010，42(6):213-218．

［12］陈鹏，高亮，郝建芳．铁路曲线上轮轨磨耗影响参数的仿真研究［J］．中国铁道科学，2007，28(5):19-23．

［13］NELSON J T．Recent Developments in Ground-borne Noise and Vibration Control［J］．Journal of Sound and Vibration，1996，193(1):367-376．

［14］HUSSEIN M F M，HUNT H E M．Modelling of Floating-slab Track with Discontinuous Slab．PartⅡResponse to Moving Trains［J］．Journal of Low Frequency Noise Vibration and Active Control，2006，25(2):111-118．

［15］李成辉．轨道［M］．成都:西南交通大学出版社，2005．

［16］刘卫星，王午生．铁路碎石道床动刚度与阻尼的试验研究［J］．铁道学报，2002，24(6):99-104．

［17］张迅，苏斌，李小珍．扣件刚度与阻尼对铁路箱梁车致振动噪声的影响研究［J］．振动与冲击，2015，34(15):150-155．

［18］翟婉明．车辆-轨道耦合动力学［M］．4th．北京:科学出版社，2015．

［19］方锐，肖新标，房建英，等．轨道结构参数对钢轨和轨枕振动特性的影响［J］．铁道学报，2011，33(3):71-76．

Research on Dynamic Stiffness Characteristics of Ballast Track withⅢ-type Sleepers

QI Wei，LI Chenghui，ZHENG Jian，LIU Yutao
(Key Laboratory of High-speed Railway Engineering，Ministry of Education，Southwest Jiaotong University，Chengdu Sichuan 610031，China)

Dynamic stiffness is animportantparameterreflectedthedynamic characteristics oftrack．T he relationships between track dynamic stiffness and some parameters of track structure，including fastening stiffness，fastening damping，ballast bed stiffness were analyzed by building ballast track model withⅢ-type sleeper in this paper．T he results show that with the increase of fastening stiffness，the frequencies of the first anti-resonance，the second resonance and the fluctuation amplitude of track dynamic stiffness increase，while the track dynamic stiffness increases in low frequency and decreases in middle and high frequency．W ith the increase of the fastening damping，the amplitude of track dynamic stiffness decreases．W hen the fastening damping is 75 kN·m/s，the fluctuation amplitudes of track dynamic stiffness in middle frequency and high frequency are greatly reduced．T he increase of ballast bed stiffness causes the frequencies of first resonance and anti-resonance increase，meanwhile，causes the amplitude of track dynamic stiffness decrease in low frequency．T he track resonance can be efficiently decreased by decreasing fastening stiffness and increasing fastening damping and ballast bed stiffness，which can be realized the comfortability requirements of dynamic geometry on ballast track．

High speed railway;Ballast track;Dynamic stiffness;T rack parameter;Excitation frequency

U211．3

A

10．3969/j．issn．1003-1995．2016．12．24

1003-1995(2016)12-0090-04

(责任审编郑冰)

2016-08-24;

2016-10-25

国家自然科学基金高速铁路基础研究联合基金(U1334203，U1234201)

亓伟(1989—)，男，博士研究生。