长江流域经济发展效率与生态环境补偿机制研究

李政通，白彩全，姚成胜，杜 涵（1.南昌大学 a.经济管理学院；b.计量经济研究会，南昌 001；.山东大学 经济研究院，济南 50100；.大连理工大学 人文与社会科学学院，辽宁 大连 11604）

长江流域经济发展效率与生态环境补偿机制研究

李政通1a,1b，白彩全2，姚成胜1a，杜 涵3
（1.南昌大学 a.经济管理学院；b.计量经济研究会，南昌 330031；2.山东大学 经济研究院，济南 250100；3.大连理工大学 人文与社会科学学院，辽宁 大连 116024）

文章运用Malmquist指数分析模型与重复博弈模型对长江流域各省市的农业投入生态效率与工业投入生态效率进行研究，探索建立流域内生态补偿机制。研究结果表明：流域内各省份分别存在比较优势与绝对优势；建立流域内生态补偿机制具有必要性；存在三种补偿方式，且补偿应按梯度进行。

长江流域；生态补偿；Malmquist指数分析模型；重复博弈

0 引言

区域经济发展与生态环境的关系十分密切，且在生态环境日益突出的时代得到更多地关注，如何在促进经济发展中保护生态环境成为学者们研究的重要课题。长江流域是一个包括9省2市横跨东西的带状区域，2014年国家提出建设“长江经济带”，并对长江经济带的范围进行界定，覆盖整个长江流域。在此背景下，长江流域将面临巨大的发展契机，而各地经济发展差异较大，资源禀赋状况不同，如何在建设长江经济带的过程中协调地区发展并保护地区生态环境成为国家规划的重要任务。

近年来，我国学者对生态补偿机制进行了广泛且深入的研究[1～5]，就目前的区域经济发展与生态补偿机制或其他补偿机制而言，主要是运用博弈论方法进行经验分析，这种经验分析可以揭示区域间补偿机制的原理，但也存在着显著的局限性，并不能很好地区分地区经济发展的禀赋优势。在此情况下，本文运用DEA方法中的Malmquist模型对长江流域11省市的面板数据进行效率评价，得出各地区的资源禀赋优势，并从长江流域整体发展的角度探索建立合理的区域经济发展与生态补偿机制。

1 指标选取与数据说明

1．1 指标选取

从目前我国的产业结构来看，工业仍然是我国各地区的主要产业，农业在我国各地区所占的比重逐步下降。相比较工业和农业而言，服务业的范围较广，且在一定程度上存在与工业、农业À叉的现象。为此，本文仅考虑一个地区的工业和农业禀赋优势。而考察地区的禀赋优势的办法则是采用Malmquist方法对工业和农业的生态产出效率进行测度，得到前文所述的绝对优势和相对优势。Malmquist方法是基于投入产出分析的面板数据分析方法，衡量的是动态相对效率。在进行Malmquist方法分析之前，首先需要确认投入与产出的指标，其次进行效率测度。为此，本文建立了农业投入的生态环境产出和工业投入的生态环境产出模型。在农业投入中，本文选取农用机械总动力、农作物总播种面积和固定资产投资这三个指标；在工业投入中，选用了规模以上工业企业单位数、规模以上工业企业资产和规模以上工业企业固定资产这三个指标；而在生态环境产出方面，选用了森林覆盖率、城市生活垃圾无害化处理率和城市生活垃圾清运量三个指标。

1．2 数据说明

由于本文研究的是长江流域区域经济发展与生态环境补偿机制，建立了评价各省市农业投入的生态环境效率及工业投入的生态环境效率模型，并确定了相关的投入产出指标。为保证数据的完整性，本文选取了2000—2013年的各省市的各指标数据。数据来源于各省2001—2014年的统计年鉴。在数据搜集及处理过程中，个别指标和个别年份存在数据缺失的现状，为此本文运用几何平均法计算出现有数据的年增长率，运用年增长率对数据进行估计，保障数据的完整性。

2 模型建立

2．1 Malmquist指数分析模型

Malmquist指数分析模型是基于面板数据分析的动态相对效率评价方法[6]，Malmquist指数方法反应的是从t到t+1期的生产率变化，而t+1期的生产率变化是基于t期的技术水平条件的。其表达式为：

在式(1)中，xt、xt+1分别表示在时期t和t+1期的投入向量，yt、yt+1分别表示在时期t和t+1期的产出向量；Dt则表示t期基于产出的距离函数，也即在固定投入与既定生产技术条件下实际产出与最大可能产出的比值。同样地，在时期t+1的技术条件下，从时期t到t+1的生产率变化可表示为：

为了避免时期选择的随意性可能导致的差异，Caves等(1982)[7]建议采用Mt和Mt+1的几何平均来计算Malmquist指数：

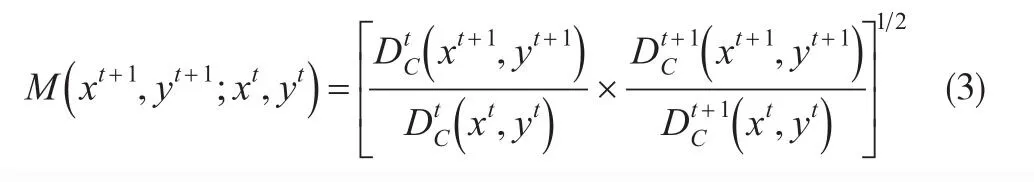
该指数反映了在固定规模报酬（用下标C表示）下，每个决策单位从时期t到t+1，全要素生产率的改进情况。如果M＞1，表明生产率呈现上升趋势；反之则表明生产率呈现衰退趋势。

Fare等(1994)[8]把Malmquist生产率指数分解为技术效率变化指数（Technical Efficiency Change,简称TEC）和技术水平变化指数（Technical Change,简称TC）：

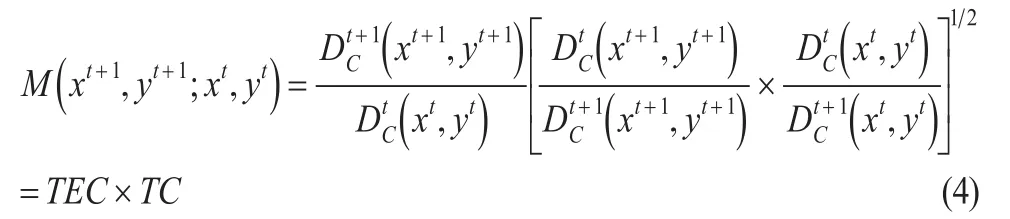
这里，TEC和TC都以固定规模报酬来定义。其中，TEC是规模报酬不变条件下技术效率的变化指数，它测度了从时期t到t+1每个决策单位到生产前沿面的距离。若TEC＞1，表明决策单位的当期生产比上一期更接近生产前沿面，相对技术效率有所提高，反之亦然。TC则测度了从时期t到t+1期间，决策单位生产前沿面的外移程度。若TC＞1，表明本期前沿面向外移动，即出现了技术进步，否则表明技术维持在原来水平上（TC=1）甚至出现了倒退（TC＜1）。

2．2 完全竞争情况下的重复博弈模型

本文建立一个重复博弈模型对区域内生态补偿机制进行研究。假设博弈的周期为一年，那么每年就是一个博弈阶段；而在跨时间的条件下，存在着资金(指收益)的时间价值，因而存在着贴现系数(r)。

假设在第一阶段，生态区的选择是发展污染较大但产值较高的产业(注重经济)或发展较为生态但产值较低的产业(注重生态)，经济区的选择是对生态区进行生态环境补偿或不进行生态环境补偿。当生态区选择发展较为生态但产值较低的产业且经济区选择补偿时，两者的得益为(W0+δ，R0-δ)；当生态区选择发展较为生态但产值较低的产业，而经济区却选择不补偿时，得益为(W0,R0);当生态区选择发展污染较大但产值较高的产业，而经济区选择补偿时，得益为(K0+δ，S0-δ);当生态区选择发展污染较大但产值较高的产业而经济区选择不补偿时，得益为(K0, S0)。其中δ表示经济区对生态区的补偿额度，是多种补偿措施量化的经济价值，这会使生态区的得益增加，但也会使经济区的得益减少，表示利益在生态区与经济区之间的单向流动。因而，补偿收益要大于不补偿收益；在补偿确定的情况下，发展较为生态但产值较低产业的收益要小于发展污染较大但产值较高产业的收益，即：K0＞W0且R0＞S0。合理的补偿会使δ介于合理的区间之内，这样会使(多，补偿)的得益要大于(少，不补偿)，也即W0+δ＞K0且R0-δ＞S0。因此，最佳的补偿应该处于(K0-W0,R0-S0)之间。图1展示了生态区与经济区的博弈矩阵：

图1生态区与经济区博弈矩阵

(1)纳什均衡与触发策略

从图1可以看出，当生态区注重生态时，经济区的最佳选择是不补偿；当注重经济时，经济区的最佳选择仍然是不补偿。从生态区的得益考虑，当经济区的选择是补偿时，其最佳选择是注重经济；当对方选择是不补偿时，最佳选择仍然是注重经济。因而，该博弈存在唯一的纯策略纳什均衡：(经济，不补偿)。此时，纳什均衡并不是最佳策略，博弈陷入了“囚徒困境”，也即该博弈中存在比(经济，不补偿)更好的策略选择，也即(生态，补偿)。

生态区与经济区都清楚自身的得益，也清楚在合作的情况下会获得更大的收益，同时也清楚这是一个不限次数的重复博弈。因此，在博弈的最初阶段，两个博弈方都可以试探性地进行合作，一旦发现对方不合作，将永久采取报复措施，这在博弈中被称为“触发策略”。在图1所示的博弈中，生态区与经济区可以在第一阶段选择合作，即生态区选择注重生态，而经济区也同时选择对生态区进行适当补偿，因而(生态，补偿)就是本文博弈的“触发策略”，其本质显示了博弈方寻求合作及利益最大化的期望。

(2)无限次重复博弈分析

在该博弈中，存在一个纯策略纳什均衡，同时存在一个触发策略。在博弈的第一阶段，由于触发策略的得益要大于纯策略纳什均衡的得益，因此会在第一阶段试探合作。一旦对方不合作，将永远采取报复措施。因而对于生态区而言，其策略选择为：第一阶段，试探合作，注重生态发展，防止经济发展带来生态恶化；第二阶段，若第一阶段的经济区采取合作策略，即对生态区进行补偿，则在第二阶段选择注重经济发展；第三阶段及以后，由于经济区能够观测到生态区在第二阶段的选择，因而会采取报复措施，之后的策略均为唯一的纯策略纳什均衡。相反，对于经济区而言，在第一阶段选择合作，如果生态区第一阶段选择合作；则第二阶段选择不合作(不补偿)，并在第三阶段及以后都将选择不补偿。考虑到资金的时间价值，同时假设贴现系数是不变的。因而，在第二阶段，生态区不改变策略(采取继续合作的策略)的条件是：

因而可得：

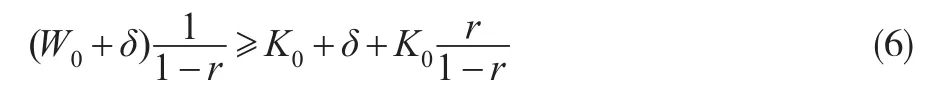
最后解得，当r满足以下条件时，生态区不会改变策略：

同理可得，经济区不会改变合作策略的条件是：

式(7)表明生态区不会改变合作的策略，式(4)表明经济区不会改变合作的策略。通过式(7)和式(8)可以得出，不管是生态区还是经济区都不会改变合作策略的条件是：

式(9)显示了贴现率与策略选择的关系，当市场贴现率满足以上两个条件时，生态区与经济区都不会改变合作的策略，即最终的策略都是(生态，补偿)。同时，贴现率是与市场利率存在关系的，r=1/(1+i)，其中，i表示市场利率。当市场利率越大时，贴现率就越小，补偿的可能性就越小，就容易发生偏离；当市场利率越小时，贴现率就越大，就越可能持续补偿。当市场利率变大到一定程度，就不会产生补偿，最终导致双方永久不合作。这在一定程度上危害市场，对生态区与经济区造成巨大的利益损失。而市场利率的波动受很多因素的影响，经济区对生态区的补偿对双方都是有好处的，于是政府就需要在补偿中间进行调节，推动补偿持续进行。

3 实证分析

3．1 长江流域各省市经济投入的生态产出效率

3.1.1 农业投入的生态产出效率

首先，本文对长江流域各省的农业投入生产环境产出效率进行测度，比较分析长江流域各省市的农业投入效率动态变化过程。Malmquist生产率指数可以分解为技术效率变化指数和技术水平变化指数，由于文章篇幅的限制，在此仅展示Malmquist生产率指数。如表1所示。

从表1可以看出：(1)长江流域整体农业投入的生态效率呈现衰退趋势。除上海和浙江之外，其他省份近年均呈现不同程度衰减。(2)经济发达省市的农业投入生态效率发展趋势要优于经济发展较差的省份。从各省市Malmquist生产率指数的平均值可以看出，上海和重庆的农业投入生态效率呈现增长趋势，且经济发展水平较高的省市要比经济发展水平较低的城市高。(3)粮食主销区的农业投入生态效率发展趋势要好于粮食主产区。上海与浙江这两个粮食主销区的农业投入生态效率排名靠前，而安徽、江西、湖北等粮食主产区的农业投入生态效率则排名靠后。

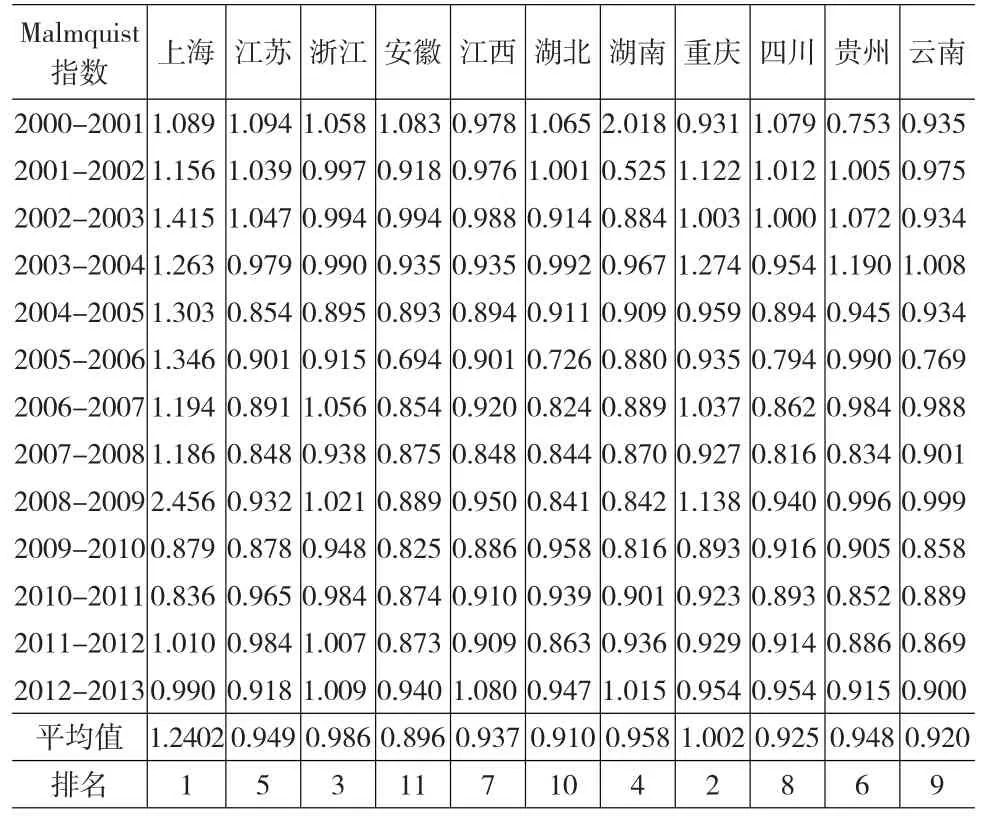
表1 长江流域各省市农业投入的生态产出相对效率

3.1.2 工业投入的生态产出效率

同理，本文对长江流域的各省市工业投入生态效率进行测度，如表2所示。

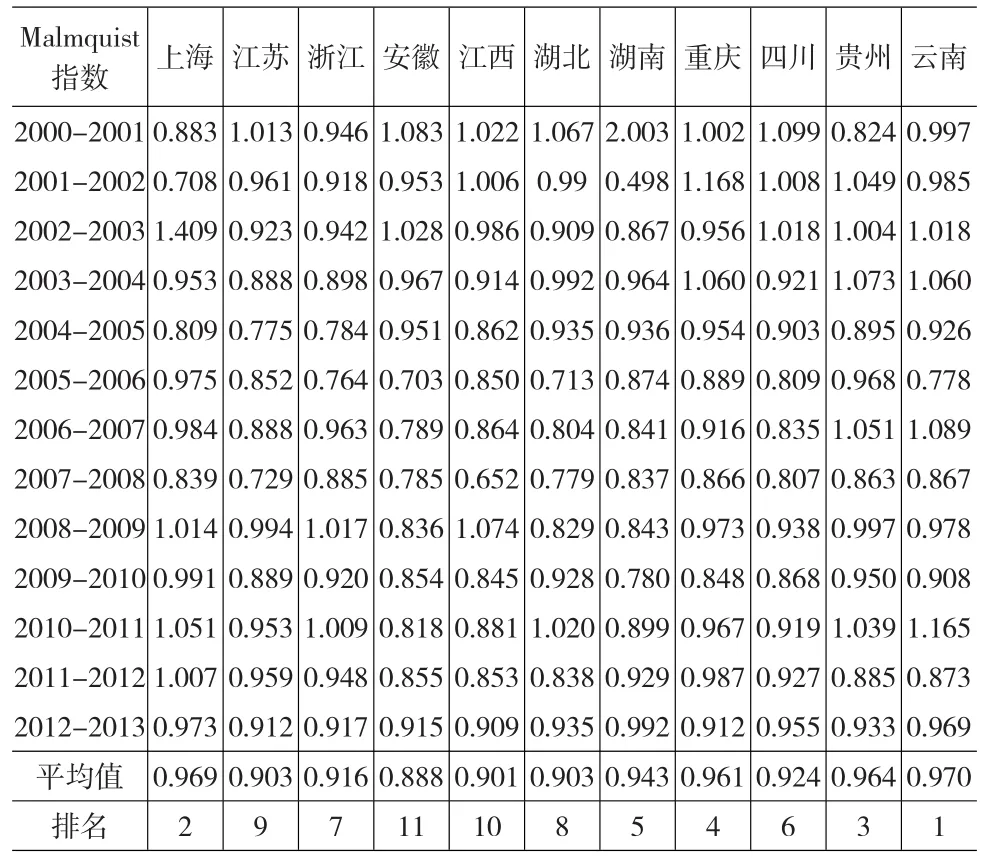
表2 长江流域各省市工业投入的生态产出相对效率

从表2可以看出：(1)长江流域整体工业投入的生态效率呈现衰退趋势。近年来，长江流域各省市工业投入的生态效率存在不同程度的衰退，这表明工业投入对生态环境的破坏作用日益明显。(2)工业投入的Malmquist生产率指数平均值呈现两边低中间高的分布。安徽、江西和浙江是工业投入的生态效率衰减最为严重的地区，而上海及长江流域的西部相关省份工业投入的生态效率衰退程度较轻。

3.1.3 经济、生态发展的比较优势与绝对优势

表1和表2分别显示了长江流域各省农业投入与工业投入的Malmquist生产率指数及其排名情况，综合表1和表2可以得到长江流域各省在生态环境背景下的比较优势和相对优势。为了更加直观地展示长江流域各省的比较优势与绝对优势，本文将前1～5作为高效率，6～11作为低效率地区。具体如图2所示。

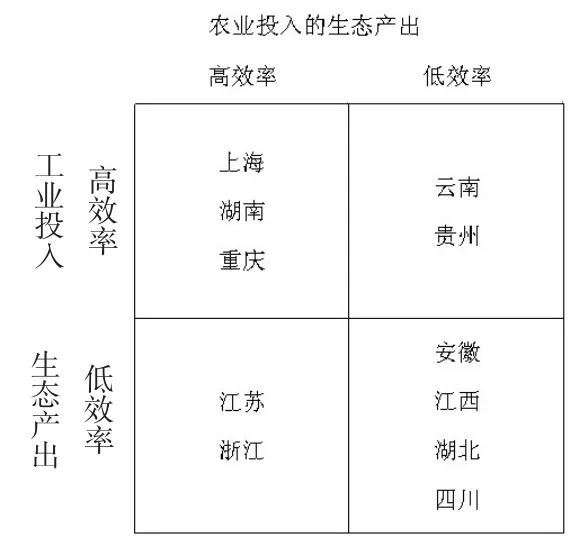
图2长江流域经济、生态发展比较优势与绝对优势

图2将长江流域各省市的经济投入生态产出效率进行归类，从图2中可以看出，农业投入与工业投入的生态产出效率高—高分布的有上海、湖南和重庆；农业投入的生态产出较高，但工业投入的产出较低的高—低分布有江苏和浙江；农业投入的生态产出较低，但工业投入的生态产出较高的低—高分布的只有云南；农业投入与工业投入的生态产出效率低—低分布的有安徽、江西、湖北和四川。

从图2中可以得出，高—高分布的上海、湖南和重庆相对于低—低分布的安徽、江西、湖北与四川而言具有比较优势。上海、湖南和重庆的经济投入生态产出效率要高于安徽、江西、湖北与四川四省，从各省市经济发展情况来看，上海与重庆是直辖市，人口、资金与技术密集，经济发展水平较高，应该着重发展产值较高的产业；湖南虽然处于高—高分布地区，但是我国的粮食主产区，重要的农业发展基地，具备农业发展的优势条件，同时湖南的科技水平、经济发展水平都较高，为此湖南一方面要注重农业发展，另一方面要提高工业发展水平。而处于相对优势的安徽、江西、湖北与四川，都是我国重要的粮食主产区，农业在地区经济发展中占据重要地位，相比较于上海与重庆，这四个省份具备发展生态农业的比较优势。为此，安徽、江西、湖北与四川一方面要努力实现农业发展向科技与资本驱动转变。

相反，高—低分布的江苏与浙江相对于低—高分布的云南与贵州而言形成绝对优势。江苏与浙江现代工业发达，经济发展水平较高，但是工业投入的生态产出效率较低，农业投入的生态效率产出却较高，而农业所占的比重并不高。相反，云南与贵州经济发展水平较低，工业化发展程度较低，但是工业投入的生态产出效率却呈现增长趋势，农业投入的生态产出效率呈现下降趋势。两者刚好形成显著的绝对优势，但与实际的经济发展情况是相违背的。因而对于江苏与浙江而言，一方面要加快工业发展升级，实现工业生产生态化；另一方面，需要对牺牲工业发展而保证流域内生态的省份进行生态补偿。对于云南与贵州而言，则需要不断改进农业生产技术，提高自身的科技水平，实现更加生态的农业生产；同时推动工业发展，实现地方经济提升。

3．2 长江流域经济发展的生态环境补偿机制

依据重复博弈的相关理论可以认为，为保证流域内生态环境处于合理的发展区间，同时由于各地区经济发展差异，就需要经济发展较好地区对经济发展较差地区实行生态补偿。由于生态补偿受到一系列因素的影响，一旦破坏合作将导致恶性竞争，为此需要政府进行协调。而运用Malmquist指数分析法对流域内各省市的农业投入生态产出效率及工业投入生态产出效率进行测度，区分出处于比较优势与绝对优势的省份。因而在进行流域内生态补偿机制的过程中，确保部分省份对其余省份的生态补偿。长江流域的生态补偿机制主要表现为：(1)高—高分布地区需要向低—低分布地区进行补偿。研究表明，安徽、江西、湖北与四川在维护流域内生态环境相对于上海、湖南和重庆具有比较优势，同时工业投入的确会对生态环境带来更大的不好影响；因而需要转变经济发展方式，既要保证农业生产，也要加快工业升级；对于安徽、江西、湖北与四川对流域内的生态环境所做的贡献，处于高—高分布的地区需要对其进行生态环境补偿。(2)高—低分布地区需要向低—高分布地区进行补偿。高—低分布地区与低—高分布地区具备生态环境的绝对优势，其中高—低分布地区具备农业生产的绝对优势，而低—高分布地区具备工业生产的绝对优势；现实却正好相反，高—低地区是我国工业发达的地区，而低—高地区则是我国农业较发达地区；流域内的生态环境靠低—高地区进行支撑，高—低地区在经济发展过程中需要着重对低—高地区进行生态补偿。(3)长江流域东部地区需要向中西部地区进行补偿。无论是从比较优势还是从绝对优势来讲，长江流域内的东部地区相关省份都应该向中西部地区的相关省份进行生态补偿。这是由于中西部地区支撑起了长江流域的生态环境但牺牲了应有的经济发展，为此东部地区有义务对中西部地区进行生态环境补偿。除东部对西部补偿的整体趋势外，中部地区的湖南及西部地区的重庆都应该对中西部地区其他省份进行一定程度的生态补偿。(4)生态补偿以贵州和云南为重。在进行生态补偿过程中，不能一概而论，而是要有梯度进行。广大中西部地区是承接生态补偿地区，而安徽、江西、湖北与四川比贵州与云南经济发展水平较高，工业基础较好，因而贵州与云南应该是重点补偿区域。

4 结论

本文的研究可以得到如下结论：(1)不同省份的不同经济发展生态产出效率存在显著差异。Malmquist指数表明，上海、湖南和重庆处于农业投入高生态产出与工业投入高生态产出的高—高分布地区，安徽、江西、湖北和四川则处于低—低分布地区，江苏和浙江处于高—低分布地区，贵州与云南处于低—高分布地区。(2)建立流域内生态环境补偿机制具有必要性。重复博弈模型给出了博弈双方不改变合作策略的条件，也即量化的补偿价值折现率要处于一个合理的区间，一旦偏离将导致流域内的恶性竞争，这既表明在流域内建立生态补偿机制具有必要性，也说明政府在建立流域内生态补偿机制中发挥着重要作用。(3)流域内生态补偿机制有三种表现形式：高—高分布地区向低—低分布地区进行补偿、高—低分布地区向低—高分布地区进行补偿，流域内东部地区对流域内中西部地区进行补偿。研究表明，高—高分布地区与低—低分布地区形成比较优势，高—低分布地区与低—高分布地区形成绝对优势，根据各地经济发展实际，处于工业投入生态产出效率比较优势省份与绝对优势省份需要向处于农业投入生态产出效率比较优势省份与绝对优势省份进行补偿；总的来看，流域内东部地区处于工业投入生态产出效率比较优势与绝对优势，而流域内中西部较多处于农业投入生态产出效率比较优势与相对优势，为此东部地区需要对中西部地区进行生态环境补偿。且补偿需要分梯度进行，针对不同的地区采取不同的补偿力度，对贵州与云南则要进行重点补偿。

[1]张建新.辽宁沿海地区经济发展与生态环境良性互动模式研究[J].经济社会体制比较,2010,(1).

[2]王军锋,侯超波,闫勇.政府主导型流域生态补偿机制研究——对子牙河流域生态补偿机制的思考[J].中国人口·资源与环境,2011,21(7).

[3]曲富国,孙宇飞.基于政府间博弈的流域生态补偿机制研究[J].中国人口·资源与环境,2014,24(11).

[4]张效军,欧名豪,高艳梅.耕地保护区域补偿机制之价值标准探讨[J].中国人口·资源与环境,2008,18(5).

[5]肖金成,李娟,戚仁广.京冀水资源补偿机制研究[J].经济研究参考, 2009,(21).

[6]Malmquist S.Index Numbers and Indifference Surfaces[J].Trabajos De Estadistica,1953,4(2).

[7]Caves D W,Diewert W E.The Economic Theory of Index Numbers and the Measurement of Input,Output,and Productivity[J].Econo⁃metrica,1982,50(6).

[8]Fare R,Grosskopf S,Lindgren B,et al.Productivity Developments in Swedish Hospitals:A Malmquist Output Index Approach[J].Data En⁃velopment Analysis Theory Methodology&Applications,1994.

（责任编辑/刘柳青）

F124.4

A

1002-6487（2016）24-0126-05

国家社会科学基金资助项目（12CJL064）；国家级大学生创新训练项目（201510403006）

李政通(1993—)，男，湖北咸宁人，硕士研究生，研究方向：计量经济学、区域经济学。

白彩全(1989—)，男，甘肃兰州人，博士研究生，研究方向：人口、资源与环境经济学。

（通讯作者）姚成胜(1977—)，男，江西上饶人，博士，副教授，研究方向：农业资源经济、区域可持续发展。

杜 涵（1993—），女，河北邯郸人，硕士研究生，研究方向：区域经济学。