Copula回归模型与应用

王 静，刘新红，吴 萍（.中国中医科学院广安门医院，北京0005；2.中国人民大学 统计学院，北京00872；.北京石油化工学院 数理系，北京0267）

Copula回归模型与应用

王 静1,2，刘新红3，吴 萍1
（1.中国中医科学院广安门医院，北京100053；2.中国人民大学 统计学院，北京100872；3.北京石油化工学院 数理系，北京102617）

文章探讨Copula回归模型应用于具有相关关系的指标时的优势，通过示例分析，揭示了用Copula回归模型与普通回归模型对数据拟合的不同，表明了当不同指标间存在相关关系时，Copula回归模型能更加客观准确地反映数据背后的关系。

Copula函数；回归模型；相关

1 Copula回归模型

Copula是一种通过单个变量的边缘分布构造多个变量的联合分布的一种数学方法，1959年，Sklar提出了Copula函数，将多元随机变量的边缘分布和它们之间的相关结构分开研究，相关结构不受边缘分布的限制。随后，很多学者发现了Copula理论在研究相关性方面的价值。Copula不仅可以反映线性相关，也能描述非线性相关。而最常用的Pearson相关系数只能反映变量间的线性相关程度，无法捕捉到非线性的关系。其他常用的一些相关性系数如Kendall's τ系数、Spearman系数和Gini关联系数等虽然能在一定程度上反映变量间的非线性相关性，但都不能全面完整地刻划变量间的相关结构。

根据Sklar定理[1]，若二维随机向量(X，Y)的联合分布函数为H(x,y)，边缘分布函数分别为F(x)和G(y)，则存在一个Copula函数C(u,v)，满足：

如果F和G是连续的，则Copula函数C是唯一确定的。

在实际应用中，常用的二元Copula函数有椭圆Copula函数和阿基米德Copula，椭圆Copula主要包括Gaussian Copula与t Copula，而阿基米德Copula除了包括常用的Gumbel Copula，Clayton Copula，Frank Copula，还包括Joe Copula、BB1 Copula等。这里只列出Gaussian Copula、Clayton Copula、Gumbel Copula和Frank Copula的具体形式，其他Copula可参考相关文献。

（1）Gauss Copula函数

其中Φ(·)为标准正态分布的分布函数。

（2）Clayton Copula函数

当θ→0时，随机变量独立；当θ→+∞时，随机变量完全相关。Clayton Copula的密度函数也具有非对称性，其密度分布呈“L”字型，即上尾低下尾高。

（3）Gumbel Copula函数

当θ=1时，随机变量独立；当θ→+∞时，随机变量完全相关。Gumbel Copula的密度函数具有非对称性，其密度分布呈“J”字型，即上尾高下尾低。

（4）Frank Copula函数

当θ→0时，随机变量独立；Frank Copula的密度函数具有对称性，其密度分布呈“U”字型。

对于两个存在相关关系的随机变量X和Y，在各自回归模型的基础上，将这种相关关系用Copula函数刻画，建立两个因变量的联合分布函数，即可建立Copula回归模型：

其中，式（2）表示了随机变量X的分布及回归模型，式（3）表示了随机变量Y的分布及回归模型，式（4）表示了随机变量X与Y的联合分布。Peter X.-K.Song等[2]在2009年用Gaussian Copula对人体烧伤面积与存活率这两个相关的结局指标进行了联合回归分析，论证了与分别单独回归分析相比，联合回归分析由于考虑了指标间的相关性，并且能得到一个结局指标关于另一个结局指标的条件分布，从而具有更高的估计效能和推断效能[4]。

例1 (2018年四川达州)如图1，二次函数y=ax2+bx+c的图象与x轴交于点A(-1，0)，与y轴的交点B在(0，2)与(0，3)之间(不包括这两点)，对称轴为直线x=2．下列结论：①abc<0；②9a+3b+c>0；③若点点是函数图象上的两点，则y1

2 应用示例

2．1 数据来源及变量选择

数据来源于某药物疗效评价试验，样本量为402例，因变量为西医量表评分差值（变量名为y1）和中医证候评分差值（变量名为y2）。自变量有药物（drug）、医院（cn）、年龄（age）、病程（bch）和基线评分（c0及zz0），除基线评分为连续变量外，其他均为分类变量。

2．2 建立普通回归模型

对因变量 y1和 y2进行正态分布检验，Kolmogorov-Smirnov检验的P值分别为0.001和0.000，均不服从正态分布。它们的偏度系数分别为0.0557和0.2245，具有明显的右偏特点，故选取逆Gumbel分布（Reverse Gumbel），这是一种极值分布，概率密度函数为：

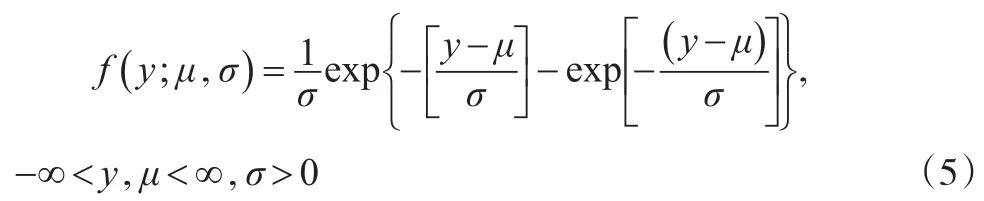
其数学期望和方差为：μ+0.5772σ和1.6449σ2。

西医量表评分差值（y1）的回归模型：

全模型：

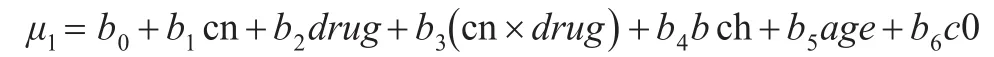
中医证候评分差值（y2）的回归模型：

全模型：

经过模型选择，剔除不显著自变量（P＞0.05），最后选定模型为：

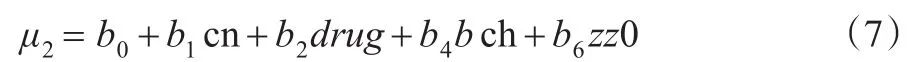
两个回归模型参数估计结果如表1所示，逆Gumbel分布的参数σ估计值分别为5.0542和4.7871。自变量drug在两个模型中都不显著，也就是说，两种药物在西医量表评分和中医证候评分改善方面，均没有显著差异。残差服从正态分布，可见，选取的分布是合适的。

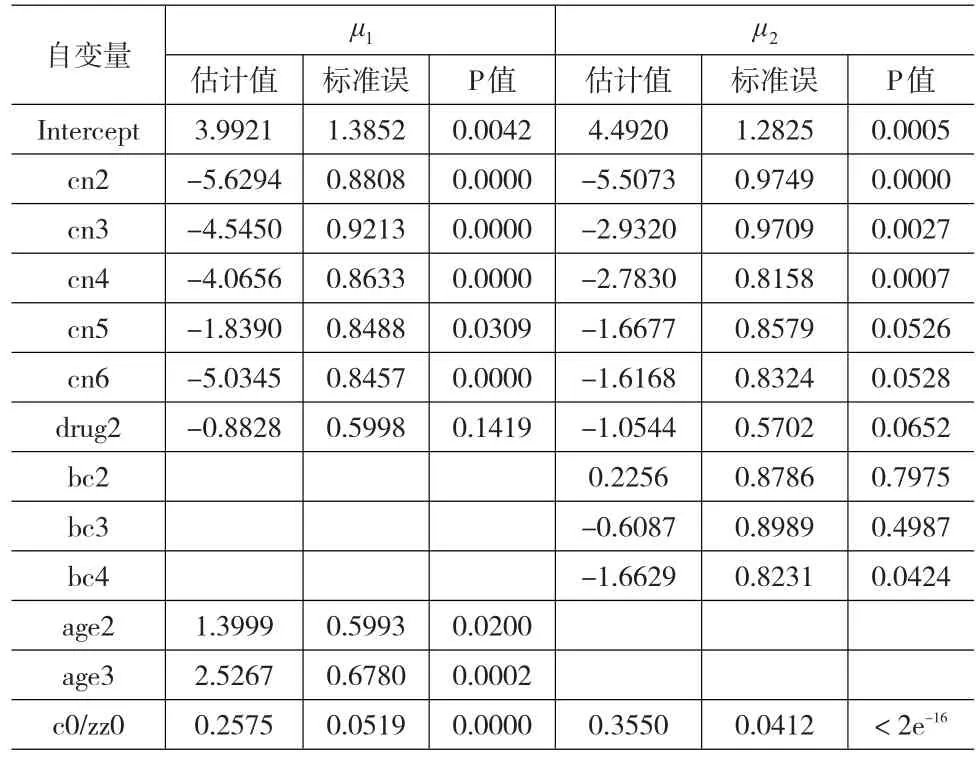
表1 μ1和μ2普通回归模型参数估计结果

2．3 建立Copula回归模型

在不考虑自变量的情况下，y1和y2的Pearson相关系数为0.6340，Kendall's τ相关系数为0.4818，表明这两个因变量是相关的。将这种相关关系用Copula函数刻画，建立两个因变量的联合分布函数，即可建立Copula回归模型。

其中，H(y1，y2)表示(y1，y2)的联合分布函数，F(y1)和G(y2)分别为y1和y2的边缘分布函数，y1，y2均服从逆Gumbel分布，密度函数见式（5），分布函数易知，C(u,v)表示Copula函数。

C(u,v)有多种选择，使用常用的Gauss Copula、Gumbel Copula、Clayton Copula和Frank Copula函数。参数估计采用极大似然法，通过R软件的GAMLSS包和CDVINE包[3,4]实现。使用4种Copula函数的回归模型的AIC值分别为2329.911、2376.840、2310.876和2318.165，可见，Clayton Copula回归模型拟合效果最好。

在Clayton Copula回归模型中，Copula函数中的参数估计值为1.3534，Kendall's τ相关系数为0.4036。 y1和y2逆Gumbel分布中的参数σ估计值分别为5.0005和5.0824，模型参数的具体估计结果见表2所示。

表2 μ1和μ2的Clayton Copula回归模型参数估计结果

将Copula回归模型估计结果与普通回归模型参数估计结果比较，可以看出自变量回归系数的点估计值相差不多，但是，中医证候评分差值回归模型中，自变量药物（drug）和年龄（age）由不显著因素变成了显著因素，也就是说，两种药物在中医证候评分改善方面有显著性差异，这也印证了Peter X.-K.Song等在2009年得出的联合回归比单独普通回归具有更高统计推断效能的结论。

3 讨论

Copula是分析相关关系的有力工具，近十年来在金融、保险、生物和医药等领域得到广泛的应用。Copula回归模型是一种考虑了因变量之间相关关系的联合回归模型[5]，当因变量之间存在相关关系时，联合回归分析比普通回归分析具有更高的推断效能，所以，用普通回归模型分析时不显著的因素，用Copula回归模型分析时可能变成显著因素。可见，当指标间存在相关性时，Copula回归模型能够揭示普通回归模型所揭示不了的差异，能够更充分挖掘数据背后的关系，从而更加客观准确地揭示隐藏在数据背后的规律。

[1]Nelsen R B.An Introduction to Copulas[M].New York:Springer,2006.

[2]Song P,Li M,Yuan Y.Joint Regression Analysis of Correlated Data Us⁃ing Gaussian Copulas[J].Biometrics,2009,（65）.

[3]Stasinopoulos M,Rigby B.Generalized Additive Models for Location Scale and Shape(GAMLSS)in R[J].Journal of Statistical Software, 2007,23(7).

[4]Brechmann E,Schepsmeier U.Modeling Dependence With C-and D-Vine Copulas:The R Package CDVINE[J].Journal of Statistical Software,2013,52(3).

[5]Kolev N,Paiva D.Copula-based Regression Models:A Survey[J].Jour⁃nal of Statistical Planning and Inference,2009,(139).

（责任编辑/浩 天）

O212

A

1002-6487（2016）24-0079-03

科技部重大新药创制课题(2013ZX09303301)；中国中医科学院广安门医院所级科研基金课题（2011S264）

王 静（1978—），女，河北唐山人，助理研究员，博士研究生，研究方向：数理统计。

刘新红（1978—），女，河北保定人，博士，讲师，研究方向：风险管理与非寿险定价。

（通讯作者）吴 萍（1960—），女，江西萍乡人，硕士，研究员，研究方向：临床试验管理。