表面粘贴式光纤光栅传感器的动应变传递规律
2017-01-09易仁慧周祖德刘明尧季冬亮
易仁慧 周祖德 刘明尧 季冬亮
武汉理工大学,武汉,430070
表面粘贴式光纤光栅传感器的动应变传递规律
易仁慧 周祖德 刘明尧 季冬亮
武汉理工大学,武汉,430070
通过理论分析,以基体承受正弦动态载荷为例,建立了表面粘贴式光纤光栅动应变传递模型,确定了影响参数;运用有限元仿真法分析了影响动应变传递的各个参数;通过实验分析验证了理论与仿真分析结果。理论与实验分析表明:振动频率、粘贴长度、粘贴厚度和粘胶中间层厚度是影响表面粘贴式光纤光栅动应变传递的主要因素,粘贴宽度对动应变传递率影响较小;激振频率远小于结构固有频率时,动应变传递率基本维持不变,实验动应变传递率为92%;激振频率达到固有频率之前,动应变传递率随激振频率增大缓慢增大;粘贴长度大于光纤光栅栅区长度的2倍时,传递率明显优于粘贴长度较短者,实验动应变传递率为92%。
光纤光栅传感器;动应变传递;动载荷;有限元仿真法;振动频率
0 引言
在结构应变检测或者传感器设计中,通常需将光纤光栅(fiber bragg grating,FBG)传感器粘贴于弹性体表面或者埋入其中,进而实时感知被测体对应的应变值[1],而粘贴层结构直接影响FBG传感器的测量精度,因此国内外许多学者对FBG传感器的静应变传递率进行了研究。Pak[2]假设光纤和涂覆层为均匀同心圆柱体,基体各向同性且受到光纤轴向远场剪应力作用,分析了涂覆层弹性模量和厚度对应力传递及应力集中的影响。Ansari等[3]根据剪滞理论,假设埋入式FBG传感器粘贴长度中心处的应变与基体应变相同,得出了光纤的轴向应变和剪应力分布。周智等[4]、周广东[5]、李天梁等[6]均对FBG传感器静应变的传递机制进行了研究。相对于FBG传感器静应变传递率研究,FBG传感器动态研究主要集中在FBG传感器解调系统方面。施纯峥等[7]设计了一套工作频率范围为100~10 000 Hz,最多测点数为4个的多点高频FBG干涉解调系统。张剑[8]设计了一套响应时间短、灵敏度高、频带宽的FBG应变传感器动态应变波长解调系统。另外孙丽[9]基于电阻应变片的动态应变传递原理,研究了光纤光栅的可测频率计算方法。静态传递率研究忽略了被测结构在实际应用中大多都会产生动态应变这一现象,而FBG传感器动态技术研究忽略了粘贴层结构对传递率的影响。本文对表面粘贴式FBG动应变传递结构进行动力学分析,提出了动力学分析的几点假设,推导出了动应变传递的力学方程。同时,通过ANSYS有限元对该模型中的影响应变传递的参数进行了研究。最后通过对不同应变传递影响参数进行实验,验证了理论仿真模型。
1 FBG动应变传递规律理论
FBG粘贴在被测基体表面进行应变测量时,其粘贴模型如图1所示,FBG粘贴长度要长于光纤光栅栅区的长度,设粘贴长度为2L,粘贴宽度为D。以光纤、保护层、胶体、基体组成的四层结构为研究对象进行力学分析,如图2所示,图中坐标原点O取在光纤光栅粘贴长度中点处,σ、τ分别表示正应力和切应力;u、ε分别表示沿光纤光栅轴向的位移和应变;x、r表示沿光纤光栅轴向和径向的距离;下标f、p、m、a分别表示光纤光栅层、保护层、胶体层和基体层。

图1 表面粘贴FBG截面示意图

图2 四层结构的力学分析图
为便于动力学分析,首先作以下假设:①各层材料均为各向同性的线弹性,基体结构沿光纤轴线方向产生均匀应变;②各层交界面结合紧密,无相对滑移。
根据牛顿第二定律,对光纤微元段受力分析得
(1)
式中,rf、dσf、ρf、uf和τ(x,rf)分别为光纤的半径、光纤微元段正应力的变化量、光纤密度、光纤微元段沿光纤轴向位移和光纤与保护层接触面的切应力。
对保护层微元段受力分析得
(2)
式中,rp、dσp、ρp、up和τ(x,rp)分别为保护层的外径、保护层微元段正应力的变化量、保护层密度、 保护层微元段沿光纤轴线位移和保护层与粘胶接触面的切应力。
对胶体微元段受力分析得
(3)
式中,D、ha、rm、dσm、ρm和τ(x,rm)分别为粘胶宽度、粘胶上底面离光纤轴心距离、粘胶下底面离光纤轴心距离、粘胶微元段正应力的变化量、粘胶密度和粘胶与基体接触面的切应力。
联立式(1)~(3),解得
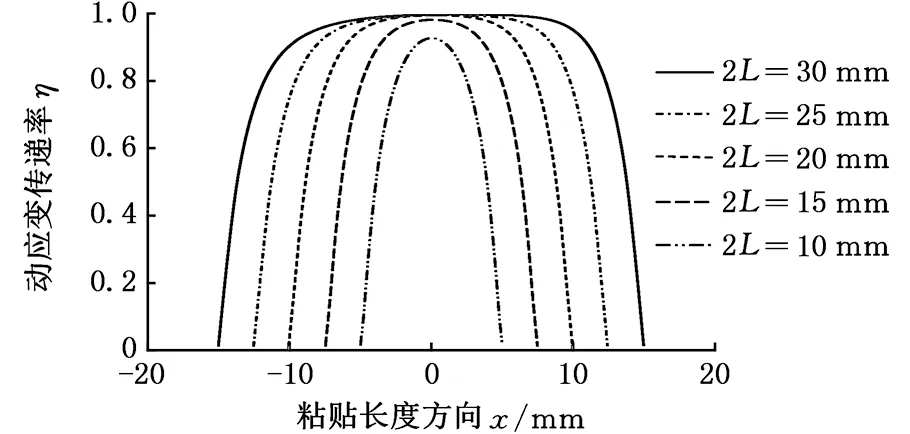
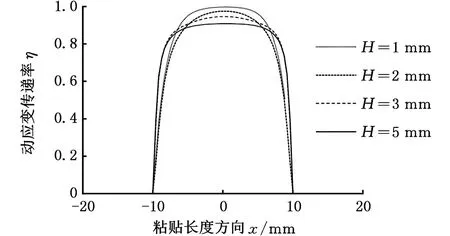
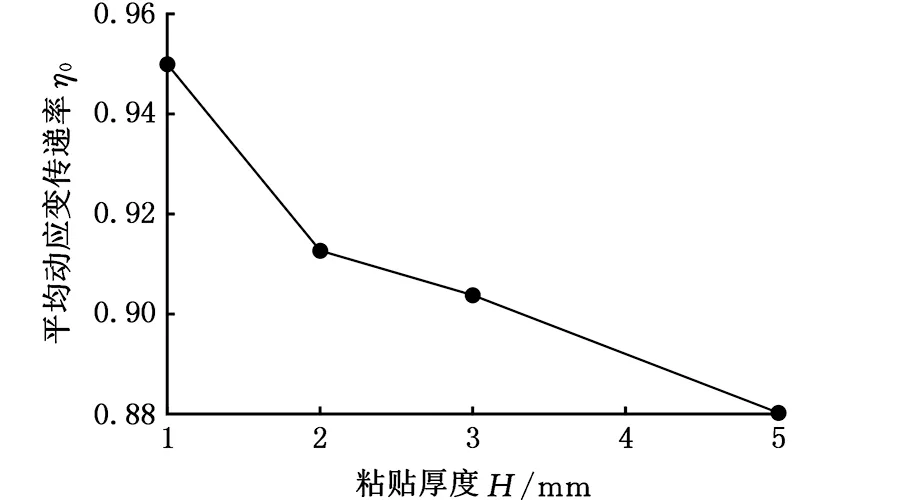
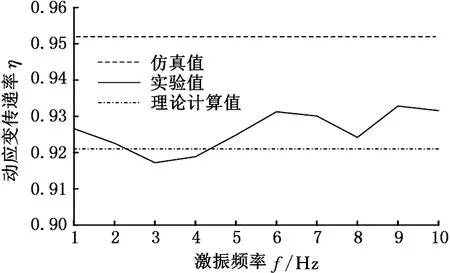
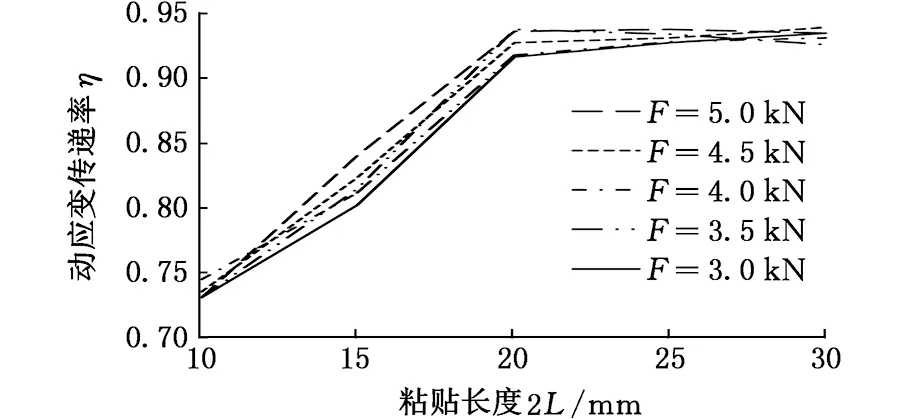
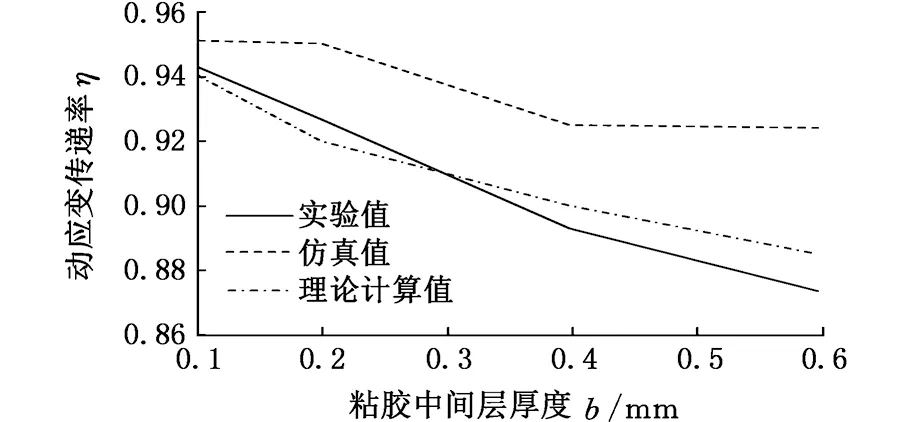
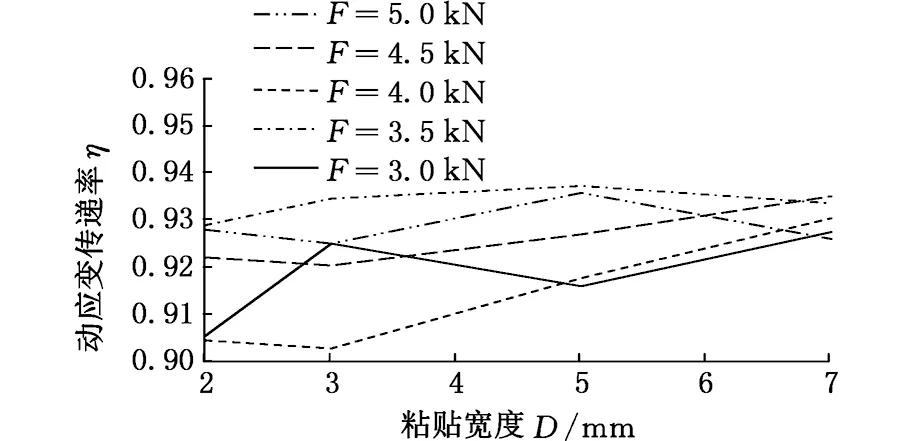
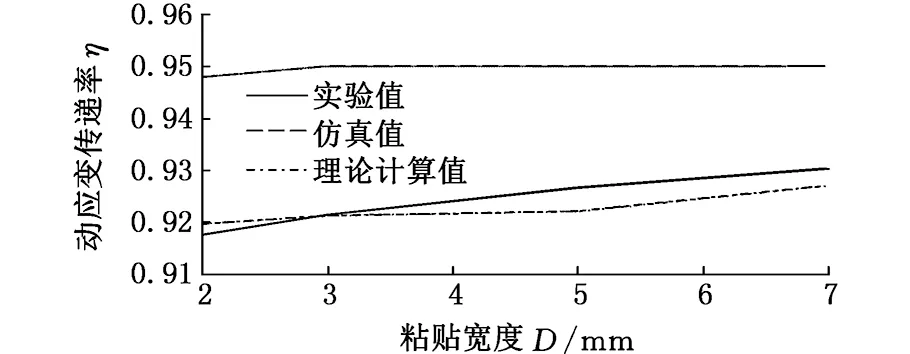
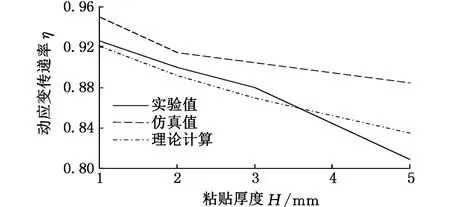
当rf (4) 当rp (5) 由于光纤光栅的长径比很大,根据材料力学应力与应变的关系σ=Eε,当剪切应力从基体结构传递到光纤时,光纤以轴向变形为主,径向变形很小,可忽略泊松效应。光纤与各层同步变形,可认为各层的应变梯度近似相等,加速度也相等,即 (6) (7) (8) (9) 式中,Gm、Gp分别为保护层和胶体层的剪切模量;Em、Ep分别为保护层和胶体层的弹性模量。 式(7)两边同时对x求导得 (10) 其中边界条件为 εf(-L)=εf(L)=0 (11) 以长度为2l、截面积为A的杆作为基体模型进行分析。因光纤光栅粘贴层很薄,弹性模量较小,为3 GPa,而基体弹性模量为210 GPa,故在计算杆的轴向运动时可忽略光纤光栅粘贴层弹性模量。左端固定,右端自由,在自由端施加简谐载荷N(t)=P0sinωt;其中P0为常数,ω为激励圆频率。坐标原点同样取在FBG粘贴长度中点处,受力分析如图2所示。由动力学原理得到波动方程: (12) 其中,ua(x,t)为杆微元段轴向振动位移;边界条件为 (13) 于是,杆的稳态反应为 (14) 动应变为 (15) 加速度为 (16) (17) (18) 平均动应变传递率为 (19) 其中,fn为传递结构的第n阶固有频率,固有频率随粘贴长度的增大而减小,因此为增大动应变测量的可测频率范围,应在保证较高的传递率下尽量减小粘贴长度。可认为传递率在90%~110%时,能获得较好的测量效果。 运用ANSYS Workbench中的瞬态分析(transient structural)模块,定义材料属性如表1所示。 表1 各层材料属性参数 建立结构模型,基体尺寸为40 mm×25 mm×15 mm,胶体尺寸为20 mm×5 mm×3 mm,光纤尺寸为φ0.125 mm×20 mm,保护层长度为20 mm,内径为0.125 mm,外径为0.25 mm,光栅轴心距离基体上表面为0.325 mm。基体沿光纤轴向一端固定,另一端施加(5500+5000sinωt)N的压力。 2.1 激振频率对平均动应变传递率的影响 由式(18)可得动应变传递率的轴向分布与时间无关,将激振频率分别设定为0.1,1,10,100,1000,10 000 Hz时,得到不同激振频率下FBG纤芯动应变传递率沿粘贴长度方向分布。当激振频率从0.1 Hz增大到1000 Hz时,FBG纤芯动应变传递率沿粘贴长度方向上的分布相同,但当激振频率为10 000 Hz时,单个位置处的动应变传递率较激振频率为1000 Hz时的动应变传递率有所增大,并且传递率平稳段的长度也增大。各激振频率下FBG的传递率平稳段的长度,即有效粘贴长度,如表2所示。求各激振频率下平稳段的传递率平均值,得到FBG纤芯的平均应变传递率η0与激振频率f的变化关系,如图3所示。FBG传感器纤芯平均动应变传递率在激振频率为0.1~1000 Hz时保持不变,其值为95%,当激振频率增大到10 000 Hz时,平均动应变传递率增大到101%。在激振频率未达到结构固有频率时,动应变传递率随激振频率的增大而缓慢增大。 表2 不同激振频率下FBG有效粘贴长度 图3 FBG纤芯平均动应变传递率η0随激振频率f的变化 2.2 粘贴长度对平均动应变传递率的影响 当激振频率设为1 Hz时,图4为不同粘贴长度下FBG纤芯的应变传递率沿粘贴长度方向的变化曲线。光纤纤芯上感应的应变传递率平稳区域随粘贴长度的增大而增大,提取各粘贴长度下FBG的有效长度如表3所示。提取图4中5个粘贴长度下平稳段的应变传递率均值,得到FBG纤芯的平均应变传递率与粘贴长度的变化关系,如图5所示。由图5可知,光纤纤芯的应变传递率随粘贴长度的变化趋于稳定,约为95%。综合表3和图5可知,当粘贴长度大于FBG传感器长度的2倍时,动应变传递率趋于平稳。 图4 不同粘贴长度下FBG纤芯应变传递率η沿粘贴长度方向x的变化 图5 不同粘贴长度2L下FBG纤芯平均动应变传递率η0 表3 不同粘贴长度下FBG有效粘贴长度 2.3 粘胶中间层厚度对平均动应变传递率的影响 当激振频率是1 Hz时,将粘胶中间层厚度b(b=rm-rp,指纤芯离基体的距离)分别设定为0.1,0.2,0.4,0.6 mm,得不同粘胶中间层厚度下FBG动应变传递率沿光纤纤芯轴向的分布。光纤纤芯感应的应变传递率平稳区域随中间层厚度的增大而减小,各中间层厚度下FBG的有效长度如表4所示,求平稳区域的动应变传递率均值,得到FBG纤芯的平均动应变传递率如图6所示。由图6可知,FBG纤芯的平均动应变传递率随粘胶中间层厚度的增大而减小。 表4 不同粘胶中间层厚度下FBG纤芯有效粘贴长度 图6 不同粘胶中间层厚度b下平均动应变传递率η0 2.4 粘贴宽度对平均动应变传递率的影响 当激振频率是1 Hz时,将粘贴宽度D分别设定为2,3,5,7 mm,得不同粘贴宽度下FBG动应变传递率沿光纤纤芯轴向的分布。光纤纤芯感应的动应变传递率平稳区域随粘贴宽度的增大而非常缓慢地增大,可认为不变。各粘贴宽度下FBG的有效长度如表5所示,得到FBG纤芯的平均动应变传递率如图7所示。由图7可知FBG纤芯的平均动应变传递率随粘贴宽度的增大而基本保持不变,维持在95%左右。 表5 不同粘贴宽度下FBG纤芯有效粘贴长度 图7 不同粘贴宽度D下平均动应变传递率η0的变化 2.5 粘贴厚度对平均动应变传递率的影响 当激振频率是1 Hz时,图8所示为不同粘贴厚度H(H=ha+rm)下FBG动应变传递率沿光纤纤芯轴向的分布。光纤纤芯感应的应变传递率平稳区域随粘贴厚度的增大而减小。提取各粘贴厚度下FBG的有效长度如表6所示,提取图8中平稳区域的动应变传递率均值,得到FBG纤芯的平均动应变传递率如图9所示。由图可知FBG纤芯的平均动应变传递率随粘贴厚度的增大而减小。 表6 不同粘贴厚度下FBG纤芯有效粘贴长度 图8 不同粘贴厚度H下动应变传递率η的分布 图9 不同粘贴厚度H下平均动应变传递率η0的变化 将FBG粘贴于质量块表面,分别控制与仿真相同的尺寸变量。本实验采用美国MTS810实验系统给图10所示的方杆加载。该加载系统载荷量程为±100 kN,工作频率为0~10 Hz。FBG解调仪为理工光科所产15波段解调仪,采样频率为4 kHz,误差为5 pm。实验中分别施加幅值下为5,4.5,4,3.5,3 kN的偏置正弦载荷。 图10 实验系统实物图 3.1 不同激振频率对平均动应变传递率的影响实验 图11 FBG的动应变传递率与激振频率的关系 图12 不同激振频率下应变传递率实验值、仿真值和理论计算值 选取栅区长度为10 mm的FBG,粘贴长度为20 mm,宽度为5 mm,厚度为1 mm,在方杆各表面粘贴光纤如图10所示。因为实验条件限制,激振频率只能控制在10 Hz以内,图11所示为不同振幅下FBG动应变传递率随激振频率的变化关系。从图11中可以发现,低频激振下,FBG动应变传递率基本稳定在92%左右,并且随着激振幅值的增大,稳定性越好。取不同激振幅值下的平均值与有限元仿真值和理论计算值对比可得图12。实验值在92%~93%范围内波动,基本保持不变,比仿真值95%偏小,但与理论计算值92%基本相等。实验证明了在激振频率远低于传递结构固有频率时,FBG传感器平均动应变传递率随激振频率增大而保持不变,部分验证了理论计算和仿真分析的结论。3.2 粘贴长度对平均动应变传递率影响实验 取栅区长度为10 mm的FBG,粘贴宽度为5 mm,厚度为1 mm,粘贴在质量块各表面上,粘贴长度分别控制为10,15,20,25,30 mm,在1 Hz的激振载荷下进行实验。图13所示为不同振幅下 FBG动应变传递率与粘贴长度的关系。从图13中可发现,当粘贴长度为光纤光栅栅区长度的2~3倍时,应变传递率趋于稳定,约为92%,比有限元仿真值95%小,但与理论计算值92%相同。由于FBG的感知应变为一定测量长度的应变均值,只有在一定粘贴长度下,FBG的应变才能更接近于被测体的真实值。提取不同激振幅值下动应变传递率平均值的实验值与仿真和理论计算值比较如图14所示。实验验证了FBG传感器平均动应变传递率随粘贴长度增大而增大,当粘贴长度达到栅区长度的2倍以上时,动应变传递率基本不变的结论。 图13 FBG动应变传递率与粘贴长度关系 图14 不同粘贴长度下FBG动应变传递率实验值、仿真值和理论计算值 3.3 粘胶中间层厚度对平均动应变传递率的影响 图15 FBG动应变传递率与粘胶中间层厚度的关系 图16 不同粘胶中间层厚度下FBG动应变传递率实验值、仿真值和理论计算值 取栅区长度为10 mm的FBG,粘贴长度为20 mm,宽度为5 mm,厚度为1 mm,粘胶中间层厚度分别控制为0.1,0.2,0.4,0.6 mm,在1 Hz激振频率下进行实验。图15为不同振幅下,FBG动应变传递率与粘胶中间层厚度的关系。由图15可知,动应变传递率随中间层厚度的增大而减小。提取图15中不同中间层厚度下FBG动应变传递率在不同激振幅值下的均值与有限元仿真值和理论计算值比较如图16所示。中间层厚度从0.1 mm到0.6 mm变化的过程中,实验测得的动应变传递率结果从94.2%减小到88.5%,比仿真值从95%减小到93%值偏小,与理论计算值从94%减小到90%相差不大。但就总体变化趋势而言,实验结果有效地验证了FBG动应变传递率随粘胶中间层厚度的增大而减小的结论。 3.4 粘贴宽度对平均动应变传递率的影响 取栅区长度为10 mm的FBG,粘贴长度为20 mm,厚度为1 mm,粘胶中间层厚度为0.2 mm,粘贴厚度分别控制为2,3,5,7 mm,在1 Hz激振频率下进行实验。图17为不同振幅下,FBG动应变传递率与粘贴宽度的关系。由图17可知,不同激振幅值下,动应变传递率都随粘贴宽度的增大而基本保持不变。提取图17中不同粘贴宽度下FBG动应变传递率在不同振幅下的均值与有限元仿真值和理论计算值比较如图18所示。粘贴宽度从2~7 mm的变化过程中,动应变传递率实验值基本维持在92%左右,比有限元仿真值95%偏小,与理论计算值92%基本相等。实验结果有效地验证了FBG动应变传递率随粘贴宽度的增大保持不变的结论。 图17 FBG动应变传递率与粘贴宽度的关系 图18 不同粘贴宽度下FBG动应变传递率实验值、仿真值和理论计算值 3.5 粘贴厚度对平均动应变传递率的影响 取栅区长度为10 mm的FBG,粘贴长度为20 mm,宽度为5 mm,粘胶中间层厚度为0.2 mm,粘贴厚度分别控制为1,2,3,5 mm,在1 Hz激振频率下进行实验。图19所示为不同振幅下,FBG动应变传递率与粘贴厚度的关系。由图19可知,不同激振幅值下,动应变传递率都随粘贴厚度的增大而减小。提取图19中不同粘贴厚度下FBG动应变传递率在不同振幅下的实验值与有限元仿真值及理论计算值比较如图20所示。粘贴厚度从1 mm到5 mm的变化过程中,动应变传递率实验值从92%减小到81%,与有限元仿真值从95%减小到89%相比偏小,与理论计算值从92%减小到84%相比相差不大。就总体变化趋势而言,实验结果有效地验证了FBG动应变传递率随粘贴厚度的增大而减小的结论。 图19 FBG动应变传递率与粘贴厚度的关系 图20 不同粘贴宽度下FBG动应变传递率实验值、仿真值和理论计算值 3.6 实验误差分析 (1)实验操作工程中产生的误差。因为在使用AB胶粘贴光纤光栅过程中,不可避免地会使粘胶中混入大量的气泡,造成胶体材料产生局部应力集中,会使测量结果大于或小于理论计算值,另外由于在粘贴过程中光纤光栅可能会与方杆轴向产生夹角,也会影响实验结果。 (2)实验系统中的误差。由于使用的光纤光栅解调仪自身带有±5pm的漂移,在使用数据处理软件分析时,也会自动地产生一定的误差。 本文推导了表面粘贴式FBG动应变传递公式,通过仿真和实验对激振频率、粘贴长度、粘胶中间层厚度、粘贴宽度和粘贴厚度等参数对应变传递率的影响进行了研究。实验与仿真对比分析表明:在小于1000 Hz低频振动时,FBG动应变传递率基本保持不变,但激振频率继续增大时,动应变传递率会缓慢增大,对本文中所述结构,当激振频率超过7290 Hz,其动应变传递率甚至超过100%;粘贴长度大于光纤光栅栅区长度的2倍时,动应变传递率明显优于粘贴长度较短者,实验测得应变传递率约为92%,综合考虑可测频率的范围,应取粘贴长度为光纤光栅栅区长度的2倍;FBG的动应变传递率随中间层厚度的增大而减小,中间层厚度取0.1~0.2 mm时应变传递率较为稳定;动应变传递率随粘贴宽度增大基本保持不变,稳定在92%;传递率随粘贴厚度增大而减小,实际应用中取粘贴厚度为1 mm能获得较高的传递率。 在使用FBG传感器时,为获得较好的传递率,粘贴长度应取光纤光栅栅区长度的2倍,粘胶中间层厚度应取0.1 mm,粘贴厚度应取1 mm,粘贴宽度应可取5 mm。 [1] 姜德生,何伟. 光纤光栅传感的应用概况[J]. 光电子·激光,2002(4):420-430. Jiang Desheng, He Wei. Review of Applications for Fiber Bragg Grating Sensors [J]. Journal of Optoelectronics·Laser, 2002(4): 420-430. [2] Pak Y E. Longitudinal Shear Transfer in Fiber Optic Sensors[J]. Smart Materials and Structures,1992,1(1): 57-62. [3] Ansari F, Yuan L. Mechanics of Bond and Interface Shear Transfer in Optical Fiber Sensor[J]. Journal of Engineering Mechanics, 1998,124(4):385-394. [4] 周智, 李翼龙, 欧进萍. 埋入式光纤光栅界面应变传递机理与误差修正[J]. 哈尔滨工业大学学报,2006,38(1):49-55. Zhou Zhi, Li Yilong, Ou Jinping. Strain Transfer Mechanism and Error Correction of FBG Interface Embedded[J]. Journal of Harbin Institute of Technology,2006,38(1):49-55. [5] 周广东. 光纤光栅传感器应变传递理论研究[D]. 大连:大连理工大学,2007. [6] 李天梁, 谭跃刚. 受弯件上粘贴型光纤布拉格光栅的应变传递规律[J]. 光学·精密工程,2015,23(5):1254-1264. Li Tianliang, Tan Yuegang. Strain Transfer Factors of Pasted FBG on Bending Part Surface [J]. Optics·Precision Engineering,2015,23(5):1254-1264. [7] 施纯峥,陈志超,何海律,等. 光纤光栅多点动应变测量系统[J]. 光子学报,2001,22:51-53. Shi Chunzhen, Chen Zhichao, He Hailü, et al. Multi-point Dynamic Strain Measurement System of Fiber Bragg Grating[J].Acta Photonica Sinica, 2001,22:51-53. [8] 张剑. 用于动态应变测量的光纤布拉格光栅波长解调技术研究[D]. 哈尔滨:哈尔滨理工大学, 2007. [9] 孙丽. 光纤光栅传感技术与工程应用研究[D]. 大连:大连理工大学, 2006. (编辑 王艳丽) Dynamic Strain Transfer Laws of Surface Bonded FBGSs Yi Renhui Zhou Zude Liu Mingyao Ji Dongliang Wuhan University of Technology,Wuhan,430070 Firstly, as structure under sinusoidal load for example, a surface bonded FBG dynamic strain transfer model was established through theoretical analysis, and the influencing parameters were determined. Then, the influences of dynamic strain transfer parameters were analysed by using the finite element simulation method. Finally, the results of theory and simulation were verified by experimental analyses. The results of theory and experiments show that the vibration frequency, the length of glue, the thickness of glue and middle layer thickness of glue have major impacts on FBGS dynamic strain transfer rate. The width of glue has minor effects on the transfer rate. When the vibration frequency is far less than the structure natural frequency, the dynamic strain transfer rate remains the same through different frequencies and the experimental value is as 92%. Before the vibration frequency achieves the natural frequency, the transfer rate increases very slowly with the increases of vibration frequencies. When the length of glue is more than 2 times of FBG length, the transfer rate will be obviously better than the rate of shorter, the experimental value is as 92%. fiber bragg grating sensor(FBGS); dynamic strain transfer; dynamic load; finite element simulation method; vibration frequency 2016-03-01 国家自然科学基金资助项目(51375359);武汉理工大学自主创新研究基金资助项目(155204006) TN253 10.3969/j.issn.1004-132X.2016.24.018 易仁慧,男,1988年生。武汉理工大学机电工程学院硕士研究生。主要研究方向为光纤光栅传感器的切削力检测。周祖德,男,1946年生。武汉理工大学机电工程学院教授、博士研究生导师。刘明尧,男,1963年生。武汉理工大学机电工程学院教授、博士研究生导师。季东亮,男,1991年生。武汉理工大学机电工程学院硕士研究生。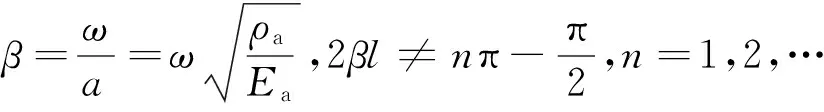

2 仿真分析









3 实验验证





4 结语
