复习课问题设计思考

马全

摘 要： 复习课量大题多，一些老师会上成习题评讲课，枯燥乏味，学生累，老师更累。复习课的目的是建立本章节的知识网络图，理解基础知识的同时学会应用，更是知识的归类、总结、升华。怎样实现上述目标？文章认为加强任务分析，精心借助问题串的设计，让学生有兴趣、举一反三，方能上好复习课。

关键词： 复习课 问题设计 复习方法

时常思考复习课怎么上？老师担心讲少了，认为复习课就是讲题、讲难题。上成了习题课不说，常常“满堂灌”，效果自然不理想。现我就工作经历谈谈复习课“问题”设计思考。

一、加强任务分析

本节课要解决什么问题做好预设，明确教学重难点。一章节的复习课学生应掌握什么？本章节知识结构图既是对各知识点的复习巩固，又使学生整体把握相互间的关联，消化理解其内涵。由学生已掌握的熟悉的力所能及的“问题”入手，通过观察对比，以旧知引新知，找准学生最近发展区，让学生发现解决问题。教师顺势而为，引导学生归纳总结，提升学生的认识。

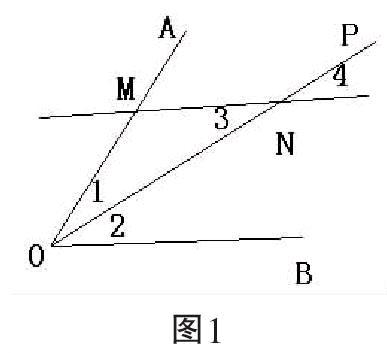
例如1：小明在做下面的作业时，因钢笔漏墨水，不小心将一部分字迹污损了，过程如下：已知OP平分∠AOB，MN∥OB。

求证：OM=NM。

证明：由OP平分∠AOB，_____________，

又由MN∥OB，知_______________，

故∠1=∠3，从而OM=NM。

小明思考：污损部分应分别是以下四项中的两项：

①∠1=∠2②∠2=∠3

③∠3=∠4④∠1=∠4

那么，他补出的是哪两项？

例如2：运用上题结论快速解答下列两题：

（1）如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC、∠ACB的角平分线，且PD∥AB、PE∥AC，则△PDE的周长是_________。

（2）如图，已知∠ABC、∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，求证：BD+EC=DE。

例1学生很易解决，可能认为仅是选两个结论。出示例2并让学生运用例1结论快速回答，就是为了设置悬念：之间有联系吗？三题要求的问题都不同。唤起学生的好奇心与探索求知欲，促使学生重新审视题1的整个过程，寻求两者之间的共性。发散学生的思维，同时培养学生应用数学的意识。适时归纳总结，让学生明白把握问题的实质解决的不是一题而是一类，提高学生的能力，升华学生的认识。

2.关注学情分析，对学生现状只有了如指掌才能有的放矢地提“问题”，因此“问题”的设置应以学生的能力为前提。哪怕一节课能突破一个难点，对学生而言就是莫大的收获。

二、体现“因学施教”

1.学生有兴趣的“问题”才是好问题。时刻以学生为主体，激发他们的兴趣，共同发现、提高。

2.孔子云：“举一隅不以三隅反，则不复也。”“回也，闻一以知十”的意思是说学习可以“举一反三”、“触类旁通”，使学生达到“由此及彼”。故复习课中尤应注重规律，强调教学知识的系统性，提高数学知识的概括水平，教会学生如何学习。故“问题串”的提出应在学生切实理解基础知识和基本原理基础之上，使学生对所学内容运用自如、触类旁通，这样的“问题”才是有效的。

例3.如图1，AB∥CD，你能证明∠B+∠D=∠E吗？

思考：图4与图5之间有联系吗？你能提出∠B，∠D，∠E三个角之间的关系吗？图6呢？请同学们互相讨论后发言。在上面的基础上进一步通过变式，激发学生的兴趣。图形在变，结论也可能在变，但解决问题的思路、方法却是一样的，让学生悟出“举一反三”其实是一种学习策略、认知策略，学会学习。“教，是为了不教”。教师在数学教学中要强调学习指导，教给学生一些认知策略、学习策略和解题策略，使学生学会学习，养成良好的学习习惯，掌握学习方法，顺利实现学习迁移。

3.通过问题情境的铺垫，变式的运用，层层递进，适时归纳总结，让学生易学，能悟出自己的东西。

三、注重练习问题的有效性

精心选题，确保练习具有趣味性、层次性、针对性和扩展性，绝不可题海战，“满堂灌”。所选“问题”应围绕本节课的主线，借助反馈练习卷的形式给予学生课内充分的自主学习时间，发挥学生的主体作用。复习课及时反馈，既是对学得好的同学的及时肯定，又有利于对本节课内容效果的及时检验，促进教学改进。如八年级证明这章：

1.如图6，已知AB∥CD∥EF，∠ABC=50°，∠CEF=150°，则∠BCE的值为（ ）

（A）50° （B）30° （C）20° （D）60°

2.请把下列证明过程补充完整：

已知：如图，DE∥BC，BE平分∠ABC.求证：∠1=∠3

证明：因为BE平分∠ABC（已知），

所以∠1=________________（ ）

又因为DE∥BC（已知），

所以∠2=________________（ ）。

所以∠1=∠3（ ）。

3.在所给图形中：

（1）求证：∠BDC=∠A+∠B+∠C;

（2）如果点D与点A分别在线段BC的两侧，猜想∠BDC、∠A、∠B、∠C这4个角之间有怎样的关系，并证明你的结论。

4.如图，在△AFD和△CEB中，点A、E、F、C在同一直线上，下面有4个判断：

（1）AD=CB;（2）AE=FC;（3）∠B=∠D;（4）AD∥BC。请用其中3个作为已知条件，余下1个作为结论，编一道数学问题，并写出解答过程。

一节课的最大成功之处在于难点的突破。尤其复习课通过问题情境的铺垫和变式的运用，层层递进，适时归纳总结，让学生易学，能悟出自己的东西。整节课老师要说得少，时刻以学生为主体，激发他们的兴趣，共同发现、提高。改变过去“满堂灌”的方式，认为复习课就是讲题、讲难题，忽略学生这个主体，忽略在原有认识上的升华。好的问题可以让复习课精彩纷呈。