伺服电机驱动连铸结晶器振动位移系统滑模控制

刘乐， 李智， 方一鸣，2， 李建雄

(1.燕山大学 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004；2.国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004)

伺服电机驱动连铸结晶器振动位移系统滑模控制

刘乐1， 李智1， 方一鸣1，2， 李建雄1

(1.燕山大学 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004；
2.国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004)

针对伺服电机驱动的连铸结晶器振动位移系统中存在减速器齿轮间隙和偏心轴机械零位偏移等问题，提出了一种基于干扰观测器的反步滑模控制方法。首先，针对减速器齿轮间隙和偏心轴机械零位偏移等扰动不确定项以及负载扰动，采用干扰观测器对其构成的复合干扰进行逼近估计，使观测误差在有限时间收敛，并将观测值动态补偿到控制器中，提高了系统的控制精确度；其次，基于反步法完成位移系统动态滑模控制器的设计，提高了系统状态的收敛速度，增强了系统的鲁棒性。仿真结果表明，所设计的干扰观测器能够准确、快速的估计出系统存在的干扰及负载转矩，且位移控制系统能够实现位移的渐近跟踪控制。

伺服电机；连铸结晶器；干扰观测器；反步控制；滑模控制

0 引 言

连铸是钢铁生产的中间环节，结晶器作为连铸环节的核心设备，对铸坯表面质量、拉坯速度的快慢起着决定性作用。目前，国内外普遍采用的连铸结晶器非正弦振动发生装置是由电液伺服系统驱动的，但其存在传动系统复杂、控制精确度低等不足。本文中的伺服电机驱动的连铸结晶器振动系统具有传动系统简化、结构紧凑等优点[1]。伺服电机是按单方向连续转动，避免了电机频繁的正反转启停。但是由于伺服电机通过联轴器、减速器、偏心轴连杆机构驱动连铸结晶器，中间机械机构存在一定的不确定性，影响了结晶器振动的稳定性。

因此，为了保证结晶器振动的平稳性，需要建立正确的系统模型并采取可靠控制算法。文献[2]建立了伺服电机驱动的连铸结晶器振动系统机理模型，为系统控制器的设计奠定了良好的基础。文献[3]采用模糊自整定PID控制器实现了连铸结晶器振动位移系统对期望波形的精确跟踪。但是,考虑到系统中存在的干扰以及负载扰动，常规的PID控制方法很难有效的对干扰进行补偿控制。文献[4]采用非奇异终端滑模负载观测器，通过使观测误差在有限时间内收敛，实现对负载转矩的估计。文献[5]和文献[6]提出的非线性干扰观测器结构简单，运算量小，且可以获得高精确度的估计值；但其假设复合干扰变化缓慢，而该假设在绝大多数情况下是不成立的，这在某种程度限制了非线性干扰观测器(NDO)的应用。

反步法是一种有效的非线性控制方法[7-8],它采用递归设计,很好地解决了对象参数不确定的鲁棒控制问题。滑模变结构控制是另一种非线性鲁棒控制方法[9-10],选取了合适的滑模面,就能够有效地抑制系统中非线性环节的影响,同时对外界干扰和参数摄动具有较强的鲁棒性。近年来，国内外学者结合反步控制与滑模控制的优点，提出了反步滑模控制方法，并将其应用到非线性系统控制器设计中。文献[11]针对非线性系统跟踪问题，提出了一种新的反步滑模控制策略，保证了闭环系统的全局鲁棒性和稳定性；文献[12]将反步滑模控制应用到永磁同步电机位置伺服系统中，并对不确定因素的上界进行了自适应估计，获得了较好的位置跟踪效果。

基于上述分析，针对机械部分存在复合扰动的伺服电机驱动的连铸结晶器振动位移系统，本文提出一种基于干扰观测器的反步滑模控制方法。首先，针对系统中存在的减速器齿轮间隙和偏心轴机械零位偏移等扰动不确定项以及负载扰动，设计非线性干扰观测器对复合干扰进行估计补偿；其次，设计反步滑模控制器，以提高系统状态的收敛速度，增强系统的鲁棒性。最后，通过仿真研究验证本文所设计控制器能够保证结晶器位移的渐近跟踪控制。

1 伺服电机驱动的连铸结晶器振动系统数学模型

伺服电机驱动的连铸结晶器振动系统装置图如图1所示。伺服电机通过减速器、偏心轴连杆机构，连接到结晶器振动台，驱动结晶器实现非正弦(或正弦)振动。该装置通过调整伺服电机的期望转速给定，可以实现结晶器按照不同波形振动。

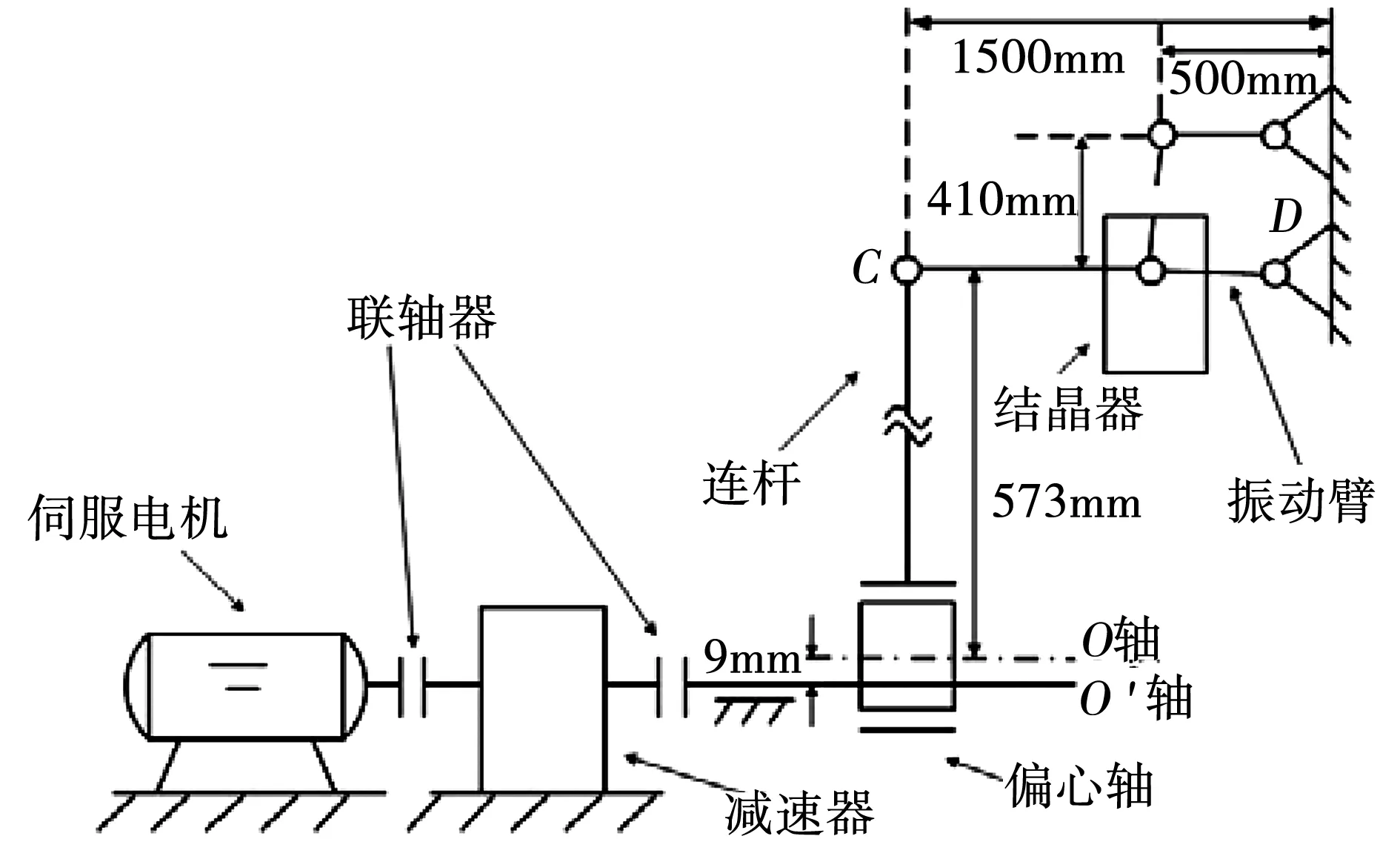
图1 伺服电机驱动的连铸结晶器振动台系统结构原理图Fig.1 Wtructure diagram of system of oscillation platform of continuous casting mold driven by servo motor

伺服电机驱动的连铸结晶器振动系统数学模型可表示为：

(1)

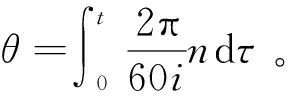
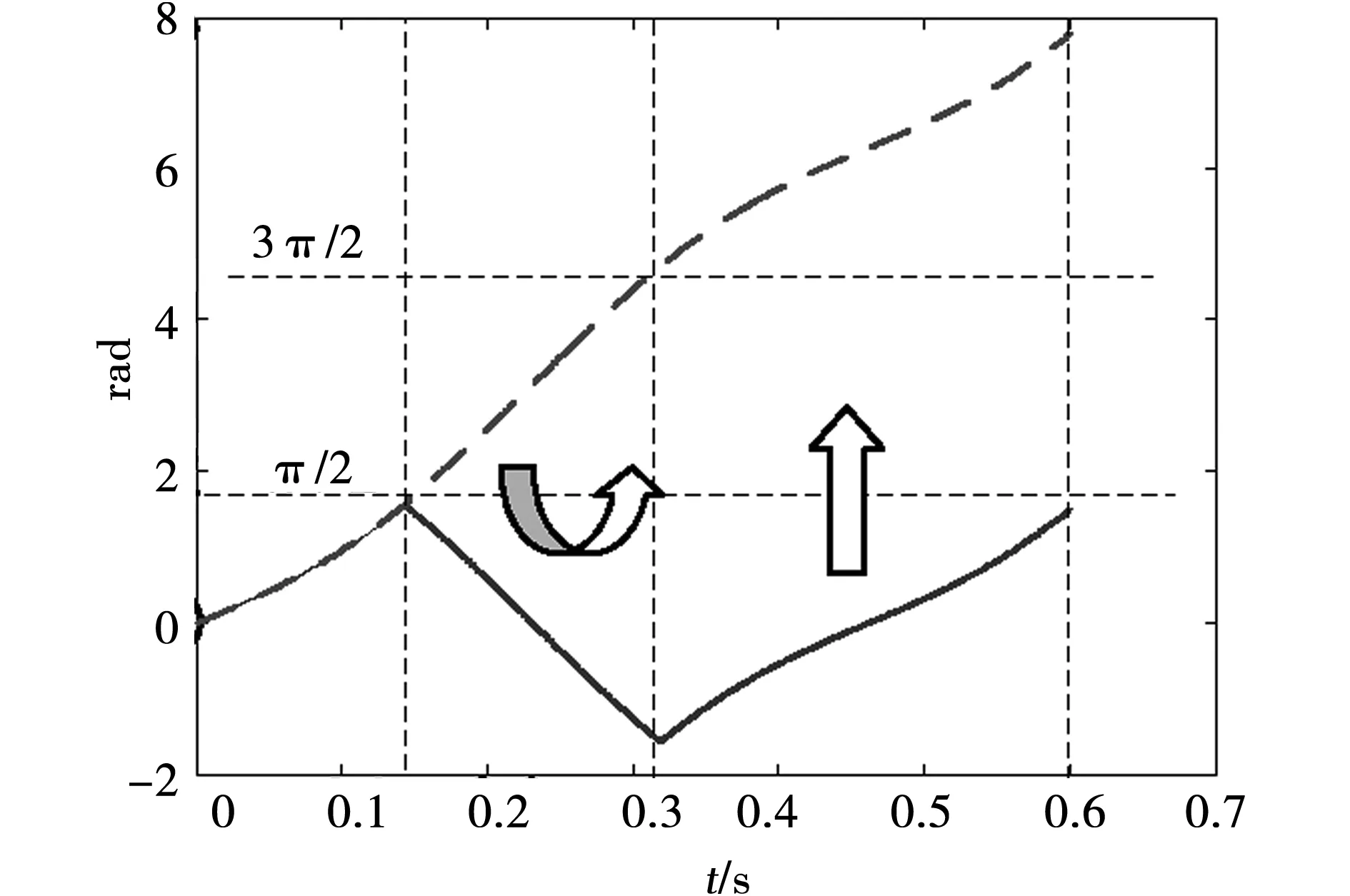
图2 偏心轴位置角转化Fig.2 Eccentric shaft Angle conversion

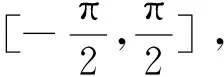
(2)

式中：tpi、tbj分别为结晶器位移曲线第i次和第j次到达波峰和波谷的时间；i∈N+、j∈N+、k∈N，xp=3sin(θ+2πζ)，k的初始值为0,当|xp|=3，k值累加1。

根据上述说明，由结晶器的位移输出xp和偏心轴的角位移θ之间一一对应的映射关系，可将式(1)转化为式(3)所示的结晶器振动位移系统等价数学模型。

(3)

式中：ud、uq为定子电压d、q轴分量；id、iq分别为定子电流d、q轴分量；L为定子绕组等效电感；ψf为转子永磁体磁链；Rs为定子电阻；p为极对数；J为转子转动惯量；B为粘性摩擦系数；TL为负载转矩；ω为转子的角速度；θ为转子角度；d为减速器齿轮间隙和偏心轴机械零位偏移存在的复合干扰。

2 伺服电机驱动的连铸结晶器振动位移系统控制器设计

2.1 干扰观测器设计

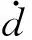
通过设计NDO来逼近估计复合干扰d

(4)

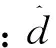
(5)

(6)

在假设1下，有

(7)

进而可得

(8)

(9)

(10)

选择p(θ)=a1θ，a1为大于零的常数。

同理，针对式(3)中存在的负载扰动设计如下NDO：

(11)

(12)

选择q(n)=a2n，其中a2为大于零的常数。

通过上述证明过程，同样能够保证负载扰动收敛到有限范围内。

2.2 反步滑模控制器设计

伺服电机驱动的连铸结晶器振动位移系统包括位置环、速度环和电流环，本节将分别完成各回路控制器的设计。

1)定义角位移跟踪误差

e1=θr-θ,

(13)

选取e1的动态滑模面为

(14)

式中c1>0。

对s1求导，有

(15)

为了提高系统在趋近阶段的收敛速度，选取指数趋近律

(16)

式中：ε1>0,k1>0。

将nr=n作为反步控制量，且nr可设计为

(17)

定义Lyapunov函数

(18)

对V1求导，并结合式(15)、式(16)和式(17)可得

(19)

2)定义转速跟踪误差

e2=nr-n。

(20)

选取e2的动态滑模面：

(21)

式中c2>0。

对s2求导可得

(22)

同样，为了改善滑模面趋近过程的动态品质，取指数趋近律为

(23)

式中：ε2>0,k2>0。

将iqr=iq作为反步控制量，将iqr设计为

(24)

定义Lyapunov函数为

(25)

对V2求导，并结合式(22)、式(23)和式(24)可得：

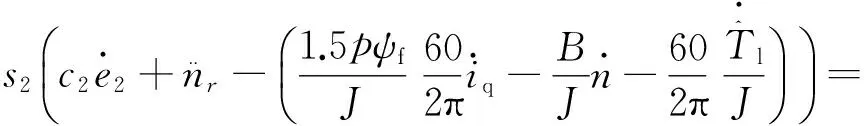
s2(-ε2sgn(s2)-k2s2)=

(26)

3)为了实现PMSM的完全解耦，采用磁场定向的id=0矢量控制方法，选取q轴控制电流如式(24)所示，d轴控制电流idr=0，并记PMSM电流跟踪误差为

(27)

对上式求导可得：

(28)

基于上述分析设计，可以归纳得到如下结论：

定理1对于如式(3)所示的伺服电机驱动的连铸结晶器振动位移系统，选取滑模面式(14)、式(21)，设计反步控制律式(17)、式(24)、式(31)和式(32)，则系统是渐近稳定的。

证明：针对如式(3)所示的系统，定义Lyapunov函数为

(29)

对上式求导，并结合式(28)可得

(30)

将电流环控制器设计为：

(31)

(32)

式中：k3>0，k4>0。

将式(31)和式(32)代入式(30)可得

(33)

由式(33)可知，所设计的控制器式(31)和式(32)能够保证整个系统渐近稳定。

3 仿真研究

为了验证所设计连铸结晶器振动位移系统反步滑模控制器的有效性，对其进行了仿真研究。伺服电机驱动的连铸结晶器振动系统结构框图如图3所示。

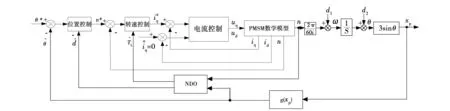
图3 伺服电机驱动的连铸结晶器振动系统整体结构框图Fig.3 Overall structure diagram of system of oscillation platform of continuous casting mold driven by servo motor

伺服电机的标称参数取为：PN=20.4 kW，nN=1 500 r/min，IN=45 A，Rs=0.14 Ω，L=4.6 mH，p=3，B=0.004，J=0.054 7 kg·m2，ψf=0.96 Wb。

所设计的反步滑模控制器参数取为：c1=130，c2=70，ε1=0.05，ε2=0.01，k1=15，k2=10，k3=150，k4=180，NDO观测器设置参数为：a1=1 000，a2=300。

仿真中采用期望的结晶器位移波形为德马克非正弦波形，其具体形式如下所示

xpr=hsin(ωt-Asin(ωt))。

仿真结果如图4～图8所示。

1)当位移给定为非正弦信号时：

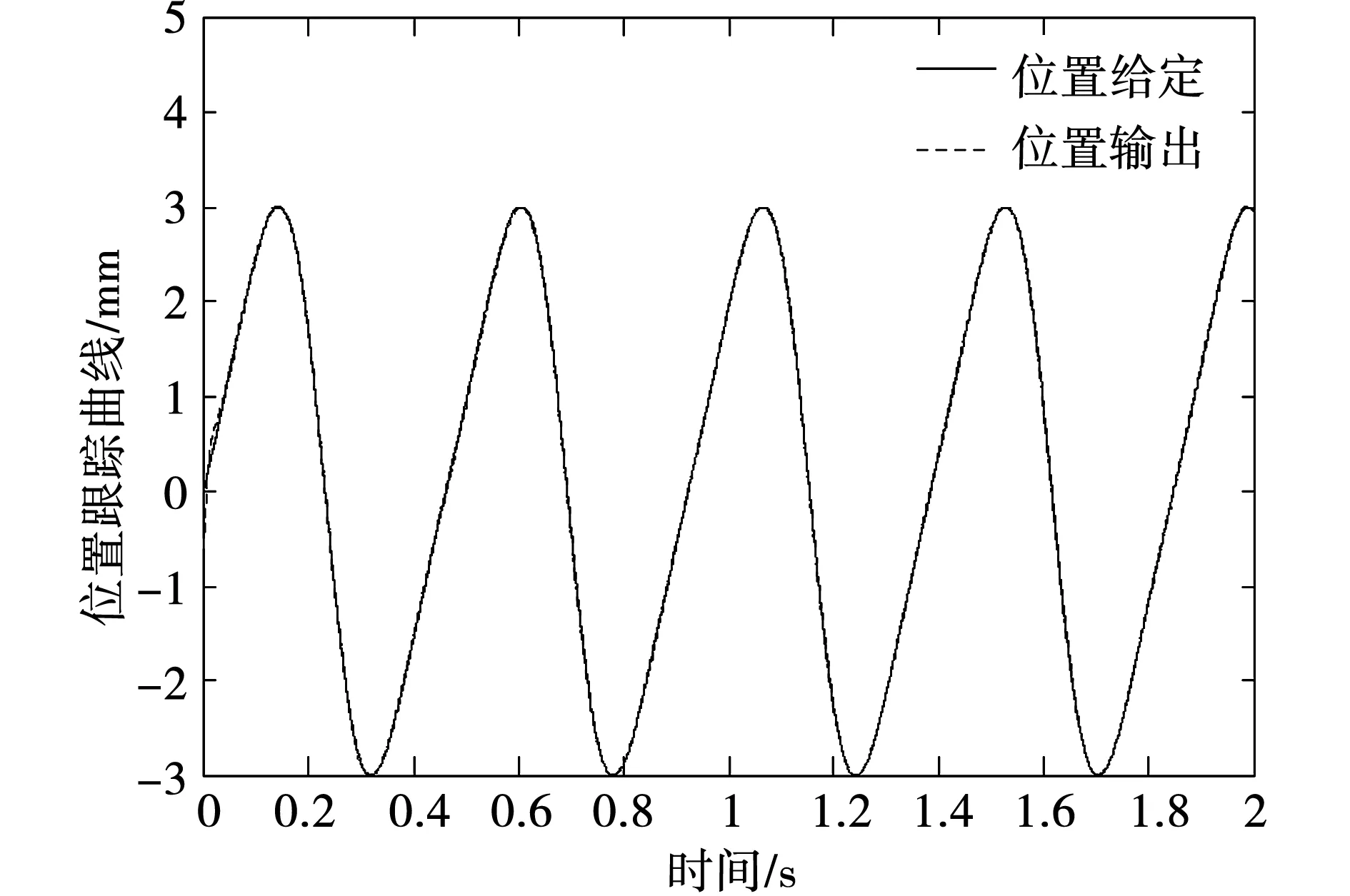
图4 结晶器位移跟踪曲线Fig.4 Displacement tracking curve of mold

图5 结晶器位移误差曲线Fig.5 Displacement error curve of mold

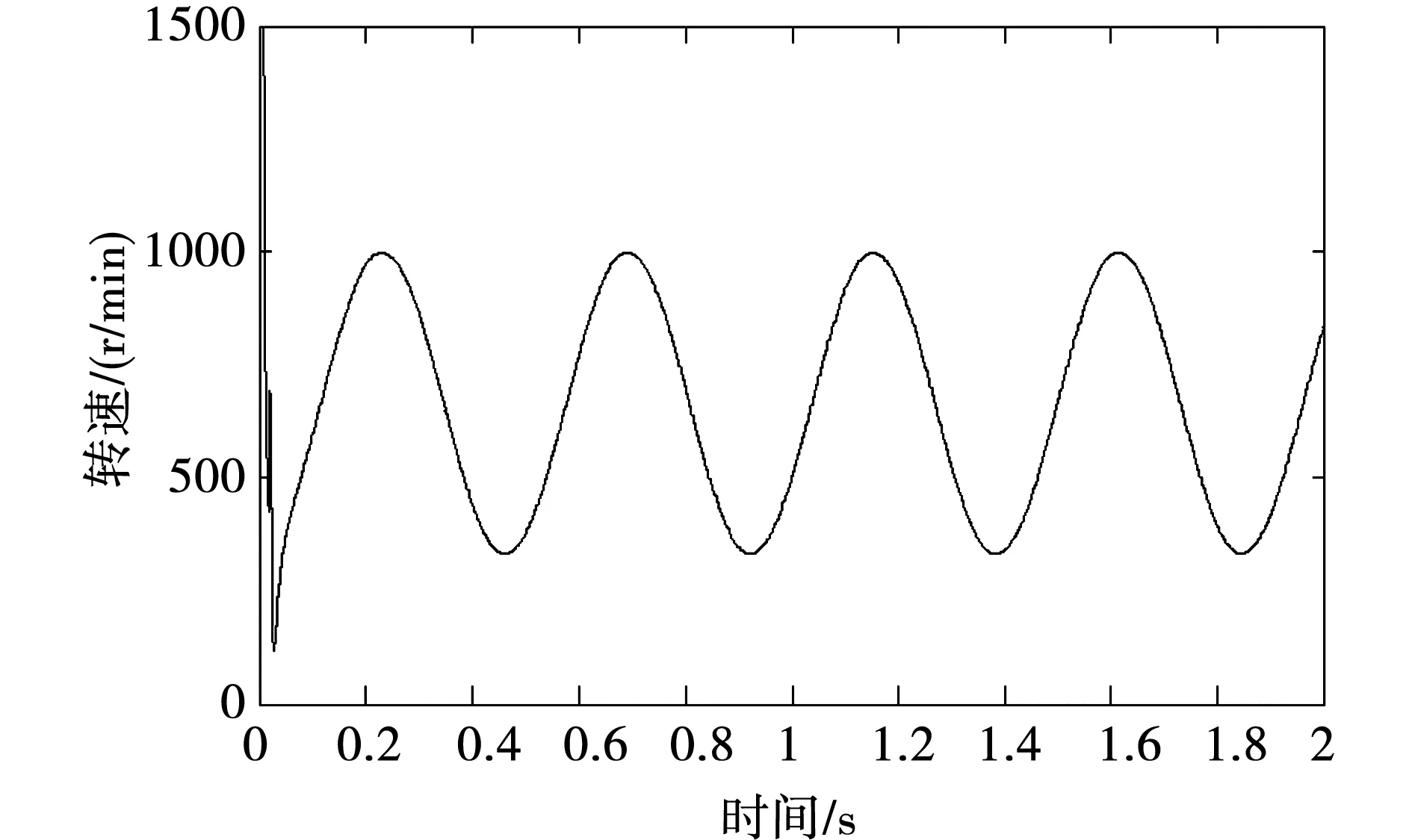
图6 电机转速曲线Fig.6 Motor speed curve

2)当位移给定为正弦信号时：

图8 结晶器位移误差曲线Fig.8 Displacement error curve of mold

由图4、图5和图7、图8可知，当系统给定为正弦或非正弦信号时，在系统存在减速器齿轮间隙和偏心轴机械零位偏移综合扰动的情况下，所设计的反步滑模控制器能够较好的实现结晶器位移输出对给定位移的渐近跟踪，抑制复合扰动造成的结晶器位移变化的能力更强。

图6、图9分别为给定信号不同情况下的伺服电机转速曲线。可以看出，电机的转速变化平稳，满足单方向、变角速度转动的要求。

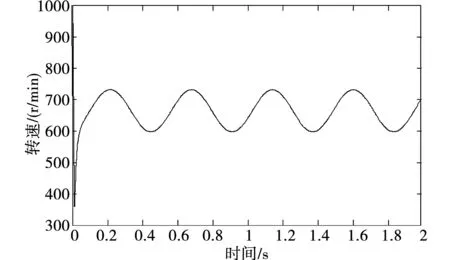
图9 电机转速曲线Fig.9 Motor speed curve

图10 综合扰动观测曲线Fig.10 Comprehensive disturbance observation curve

图11 负载TL观测曲线Fig.11 Observation curve of load TL

由图10和图11可以看出，所设计的干扰观测器能够很好的实现对系统综合扰动和负载转矩的观测估计，针对扰动的变化，能够有效地提高了系统的控制精确度。

3 结 论

本文针对伺服电机驱动的连铸结晶器振动位移系统中存在的减速器齿轮间隙和偏心轴机械零位偏移扰动问题，提出了一种基于干扰观测器的伺服电机驱动连铸结晶器振动位移系统反步滑模控制方法。该方法有效地提高了系统状态的收敛速度，削弱了复合扰动对控制系统性能的影响，增强了系统的鲁棒性。最后的仿真结果表明，所设计的NDO能够快速、准确地观测出复合干扰，设计的控制器能够保证结晶器位移的准确跟踪。

[1] 林瑞全,黄韬,张涛.一种内置式永磁同步电机复合转速估计方法[J].哈尔滨理工大学学报,2012,29(3): 84-90. LIN Ruiquan,HANG Tao,ZHANG Tao.A built-in composite permanent magnet synchronous motor speed estimation method [J].Journal of Harbin institute of technology university,2012,29(3): 84-90.

[2] 方一鸣,李宫胤,李建雄,等.伺服电机驱动连铸结晶器振动系统建模与分析[J].仪器仪表学报,2014,35(11): 2615-2623. FANG Yiming,LI Gongyin,LI Jianxiong,et al.The model and analysis for displacement system of the continuous casting mold driven by servo motor[J].Chinese Journal of Scientific Instrument,2014,35(11): 2615-2623.

[3] 亢克松,方一鸣,夏天,等.伺服电机驱动的连铸结晶器振动位移系统模糊自整定PID控制[J].燕山大学学报,2015,39(4): 334-340. KANG Kesong,FANG Yiming,XIA Tian,et al.The fuzzy self-tuning PID control for displacement system of the continuous casting mold driven by servo motor[J].Journal of yanshan university,2015,39(4): 334-340.

[4] 方一鸣,李智,吴洋羊,等.基于终端滑模负载观测器的永磁同步电机位置系统反步控制[J].电机与控制学报,2014,18(9): 105-111． FANG Yiming,LI Zhi,WU Yangyang,et al.Backstepping control of permanent magnet synchronous motor position system based on the load terminal sliding mode observer[J].Electric Machines and Control,2014,18(9): 105-111.

[5] CHEN W H.A nonlinear disturbance observer for robotic manipulators[J].IEEE Transactions on Industrial Electronics,2000,47(4): 932-938.

[6] 张元涛,石为人,邱明伯.基于非线性干扰观测器的减摇鳍滑模反演控制[J].控制与决策,2010,25(8): 1255-1260. ZHANG Yuantao,SHI Weiren,QIU Mingbo.Backstepping sliding mode control for anti-rolling fin based on the nonlinear disturbance observer[J].Control and decision ,2010,25(8): 1255-1260.

[7] EBRAHIM A,MURPHY G.Adaptive backstepping control of an induction motor under time-varying load torque androtor resistance uncertainty[J].Int J of Automation and Control,2008,2(4): 401-417.

[8] OZBAY U,ZERQEROQLU E,SIVRIOQLU S.Adaptive backstepping control of variable speed wind turbines[J].Int J of Control,2008,81(6): 910-919.

[9] 牟丽君,高存臣,李娟.一类受扰时滞离散系统的滑模跟踪控制[J].控制与决策,2008,23(8): 874-878. MU Lijun,GAO Cunchen,LI Juan.The sliding mode tracking control of a class of linear discrete system with disturbancer[J].Control and decision,2008,23(8): 874-878.

[10] CAPISANI L M,FERRARA A,MAQNANI L.Design and experimental validation of a second-order sliding-mode motion controller for robot manipulators[J].Int J of Control,2009,82(2): 365-377.

[11〗 庄开宇,张克勤,苏宏业,等.高阶非线性系统的Terminal滑模控制[J].浙江大学学报(工学版),2002,36(5): 482-485. ZHANG Kaiyu,ZHANG Keqin,SU Hongye,et al.High order nonlinear system of Terminal sliding mode control[J].Journal of zhejiang university (engineering science),2002,36(5): 482-485.

[12] 郭亚军,王晓锋,马大为,等.自适应反演滑模控制在火箭炮交流伺服系统中的应用[J].兵工学报,2011,32(4): 493-497. GUO Yajun,WANG Xiaofeng,MA Dawei,et al.Adaptive inversion sliding mode control in rocket launcher application of ac servo system[J].ACTA ARMAMENTARII,2011,32(4): 493-497.

[13] 夏天,亢克松,方一鸣,等.伺服电机驱动的连铸结晶器振动位移系统非线性处理及控制[C]//第三十四届中国控制会议,杭州,2015: 4443-4448.

[14] LI Qiang,FANG Yiming,KANG Kesong,et al.Extended state observer based nonsingular terminal sliding mode control for non-sinusoidal oscillation of continuous casting mold driven by servo motor[C]//In: Proceeding of the 34th Chinese Control Conference,Hangzhou,China,2015,1043-1048.

(编辑：贾志超)

Sliding-mode control of continuous cast Mold oscillation displacement system driven by servo motor

LIU Le1， LI Zhi1， FANG Yi-ming1,2， LI Jian-xiong1

(1.Key Lab of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao 066004,China;2.National Engineering Research Center for Equipment and Technology of Cold Strip Rolling，Qinhuangdao 066004,China)

Aiming at the problems of reducer gear clearance and the deviation of the eccentric shaft mechanical zero offset,which exist in displacement system of the continuous casting mold driven by servo motor,a backstepping sliding mode controller based on disturbance observer is designed.Firstly,For the reducer gear clearance and eccentric shaft mechanical zero offset disturbance uncertainties and load disturbances,disturbance observer was adopted to approximatly estimate the compound disturbance.The observation error in finite time convergence,and the observed value dynamic compensation to the controller,it can improve the control precision of the system was improved.Secondly,using backstepping method to design the displacement system dynamic sliding mode controller,which improves the convergence rate of the system state,and enhances the robustness of the system.The simulation results show that observer estimate the system interference and load torque quickly and accurately,and the displacement control system can track the given signal.

servo motor; continuous casting mold; disturbance observer; backstepping control; sliding mode control

2016-01-16

国家自然科学基金委员会与宝钢集团有限公司联合资助重点项目(U1260203)；国家自然科学基金(61403332)；河北省博士后科研项目择优资助(B2016003017);河北省高等学校创新团队领军人才培育计划(LJRC013)

刘 乐(1985—)，男，博士，讲师，研究方向为冷带轧机速度张力及压下系统的解耦协调控制； 李 智(1988—)，男，硕士研究生，研究方向为永磁同步电机的控制与研究； 方一鸣(1965—)，男，博士，教授，博士生导师，研究方向为自适应鲁棒控制理论与应用、冶金自动化等； 李建雄(1980—)，男，博士，副教授，研究方向为自适应鲁棒控制及理论应用。

方一鸣

10.15938/j.emc.2016.12.013

TP 273

:A

:1007-449X(2016)12-0101-08