炮控系统电动负载模拟器性能影响因素分析

王超， 侯远龙， 王力， 高强， 侯润民

(南京理工大学 机械工程学院，江苏 南京 210014)

炮控系统电动负载模拟器性能影响因素分析

王超， 侯远龙， 王力， 高强， 侯润民

(南京理工大学 机械工程学院，江苏 南京 210014)

为了抑制炮控系统电动负载模拟器中存在的多余力矩，进一步提高其输出力矩的控制精确度和动态特性，对电动负载模拟器力矩输出的影响因素进行研究。首先结合电动负载模拟器系统的结构组成和工作原理，建立数学模型，得到输出力矩对应的传递函数和具体影响因素；然后依次研究电动负载模拟器系统的连接刚度、力矩电机的输入力矩、负载电机的角度、摩擦、间隙等非线性时变量对系统力矩输出的影响，并分别采用时频阈分析和谐波跟踪等方法进行性能评估；最后结合具体仿真和实验数据，分析影响力矩电机输出力矩谐波畸变的定性和定量关系，为提高电动负载模拟器控制性能提供有力的理论支撑。

电动负载模拟器；炮控系统；力矩；非线性；时变量；谐波畸变

0 引 言

炮控系统性能是衡量武器作战能力的重要指标之一，快速、精确、稳定的调炮是实现“先敌开火、首发命中”的保证。全电式炮控系统凭借结构简单、性能优良、效率高、“二次危害”小等优点，已成为各国研究炮控系统的热点。性能优越的交流永磁同步电机驱动伺服系统的炮控系统能够极大地提高武器系统作战能力，但其仍然存在较多的非线性因素，如齿圈间隙、弹性变形、摩擦力矩等，导致该武器炮控系统出现低速“爬行”和稳态“平顶”等问题[1-3]。因此，在炮控系统研制和生产过程中，负载模拟器作为炮控、舵机等控制系统重要的专用仿真设备，用作控制系统的相关参数和带载性能验证和测试。负载模拟器的成功研制不但可以缩短控制系统的研制周期、降低研制成本，而且可以提高被加载系统的可靠性和成功率。根据加载力矩值的不同，负载模拟器可分为电液负载模拟器和电动负载模拟器，前者多用在大负载的情况下[4]，后者则凭借自身噪音和环境污染小、可靠性高、易维护等优点，广泛应用在相对较小的负载情况。目前在研的负载模拟器大多用在飞行器和船舶的舵机中[4-7]，针对提出的炮控系统电动负载模拟器研究相对较少[8-9]。

为了进一步提高炮控系统电动负载模拟器的加载精确度和快速性，传统的控制算法不能满足系统控制性能的要求，当前主要采用的研究方法是基于结构不变性原理，对电动负载模拟器系统自身存在的弹性变形、力矩电机输入力矩、负载电机角度耦合、摩擦、间隙等非线性因素进行补偿[10-18]，以及根据系统工作特点，建立针对性强的智能控制算法[19-20]。文献[10]引入弹簧杆滤除力矩的高频分量，定性分析了系统不同刚度系数对加载稳定性和快速性的影响。文献[11]和文献[12]分别采用状态观测器和在线优化的去耦滑模面来减少系统输出和输出端干扰的耦合问题。文献[13-15]结合摩擦非线性对运动控制系统产生的负面影响，建立适应性强的鲁棒控制器。文献[16-18]考虑控制系统中存在的间隙死区情况，并结合补偿控制提出合理的解决和消除方案。在上述文献的基础上，避免采用直接补偿和优化控制策略等来提高电动负载模拟器的性能，而是进一步深入分析电动负载模拟器中存在的复杂非线性对力矩跟踪性能的影响，并研究可能引起谐波畸变的因素，最后结合仿真和试验数据定性和定量的研究具体影响情况。

1 电动负载模拟器组成和数学模型

电动负载模拟器主要由主控计算机、信号调理中心、力矩电机、负载电机、电机驱动器、力矩传感器、旋转变压器、角速度传感器、角加速度传感器、惯量盘组和减速箱等构成，如图1所示。主控计算机的主要功能是对力矩传感器的反馈力矩、惯量盘组的惯性力矩等和输入力矩(指令力矩)分析计算，结合提出的算法对电动负载模拟器进行力矩跟踪控制，并计算输出控制量；信号调理中心主要用于处理来自诸多传感器的信号，并配置需要硬件执行的开关等操作按钮；电机驱动器和电机相互配合，根据主控计算机的输出，驱动器输出合适的电压来驱动电机输出相应的力矩和位置；加载端力矩传感器的作用是采集力矩电机的实际输出力矩，该力矩反馈到力矩电机输入端(主控计算机)，形成加载力矩闭环控制；旋转变压器的作用是采集力矩电机经减速箱的角度位置，用于计算此时电动负载模拟器对应的输入力矩值等；角速度传感器的作用是采集力矩电机经减速箱的角速度，为辨识方法或控制策略提供更多的系统实际量；角加速度传感器的作用是采集力矩电机经减速箱的角加速度，用于求解由惯量盘组产生的惯性力矩等；惯量盘组的功能是根据炮控系统的实际需求，选择合适的惯量盘数量，提供不同的惯性转动惯量，较为真实的模拟惯性力矩对炮控系统性能的影响。

图1 炮控系统电动负载模拟器组成图Fig.1 Composition diagram of the ELS for the GCS

电动负载模拟器的执行电机采用的是永磁交流同步电机，其具有效率高、力矩惯量比高、响应快、精确度高等特点，与采用力矩电机直接加载的方式不同，其控制电流与输出转矩不是简单的线性关系，可以采用不同的力矩控制方式。为了解决永磁交流同步电机自身耦合的问题，采用面向磁场矢量控制的电动机，可以实现电压、电流和磁势等变量的解耦。为了更好的分析和解决问题，在简化电机模型的基础上结合电动负载模拟器系统的自身特点，忽略次要因素的影响，永磁交流同步电机在电机交轴电流id=0的控制方式下可以近似地表示为直流力矩电机的模型，则可以建立如下的系统结构框图

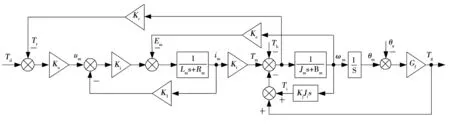
图2 炮控系统电动负载模拟器结构框图Fig.2 Structure diagram of the ELS for the GCS

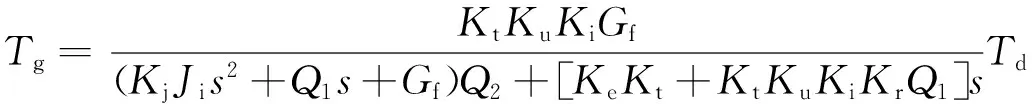
(1)

式中：Q1=Jms+Bm，Q2=Lms+Rm+KiKl。由式(1)可以知道，输出力矩Tg受弹性系数Gf、力矩电机的输入力矩Td、负载电机角度θa、摩擦和间隙等不确定因素影响较大，上述因素随工作状态实时变化，且产生原因较为复杂，呈现出较强的时变性特征，难以建立精确的机理模型。

2 连接刚度对系统性能的影响

(2)

式中Q3=Rm+KiKe。

图3为刚度系数每次增加5倍时的频率特性曲线，最高为1 250 N·m/rad。当系统的连接刚度增强时，系统的剪切频率会增加，相角特性渐渐趋于陡峭，故刚度的增加有利于提高系统带宽。但随着频宽的增加出现了较大的谐振峰值，相角在谐振频率处的特性更加陡峭，影响系统的稳定性，造成较大的多余力矩。而且机械谐振对整个机械结构有较大的破坏，在系统刚度超过1 250 N·m/rad时，必须选择合适的惯量盘进行修正。

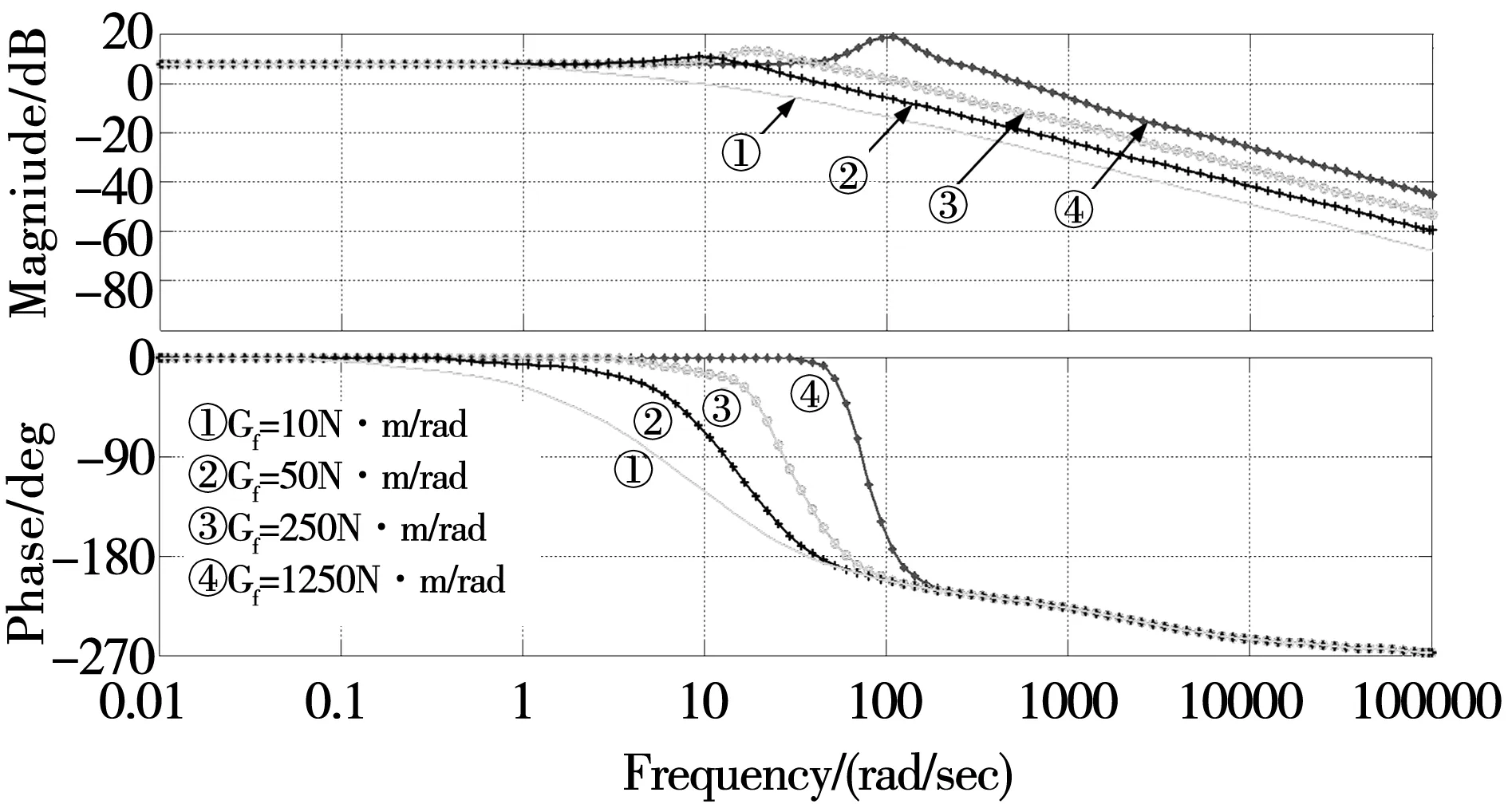
图3 连接刚度增加时频率特性比较图Fig.3 Bode comparison with the increasing Gf

3 输入力矩和负载电机角度变化对系统性能的影响

基于自主研发的炮控系统电动负载模拟器实验平台，运行已经调试好的控制程序，相关主要参数如表1所示。在负载电机匀速和正弦运动时，力矩电机输入不同幅值和频率的力矩，分析输入力矩和负载电机角度变化对系统性能的影响[6-7]。

表1 炮控系统电动负载模拟器参数表

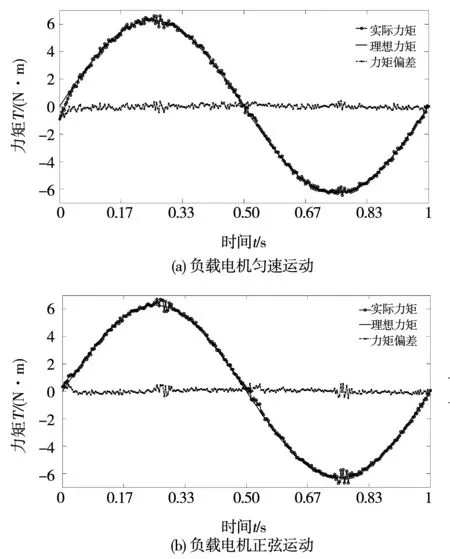
图4 输出力矩Td1=2πsin2πt实验曲线Fig.4 Curve of output torque with Td1=2πsin2πt

由图4可以知道，当力矩电机进入稳定工作状态时，在负载电机匀速和正弦运动时幅值相对误差分别是2.2%和3.0%，相位滞后分别是1.3°和2.2°，均符合指标要求(幅差<10%，相差<10°)。

其次为了分析力矩电机工作在不同频率时，电动负载模拟器系统性能的情况，使得力矩电机在负载电机工作在匀速运动时输出Td2=2πsin10πt、Td3=2πsin20πt，实验曲线如图5和图6所示。

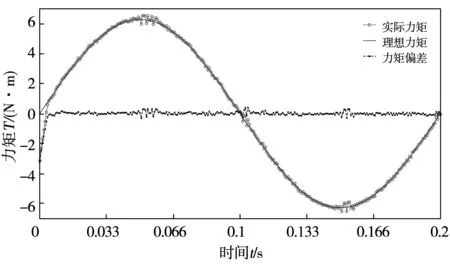
图5 输出力矩Td2=2πsin10πt实验曲线Fig.5 Curve of output torque with Td2=2πsin10πt

图6 输出力矩Td3=2πsin20πt实验曲线Fig.6 Curve of output torque withTd3=2πsin20πt

由图5和图6可以知道，当负载电机匀速运动时，在力矩电机进入稳定工作状态后，输出力矩工作频率越大，系统稳定性越差，幅值偏差越大，分别是3.3%和4.6%，相位滞后分别是2.8°和4.1°。

最后考虑力矩电机输出力矩幅值对系统性能的影响，结合上述幅值为2πN·m，此处选择负载电机工作在匀速运动时，力矩电机输出Td4=sin2πt，实验曲线如图7所示。

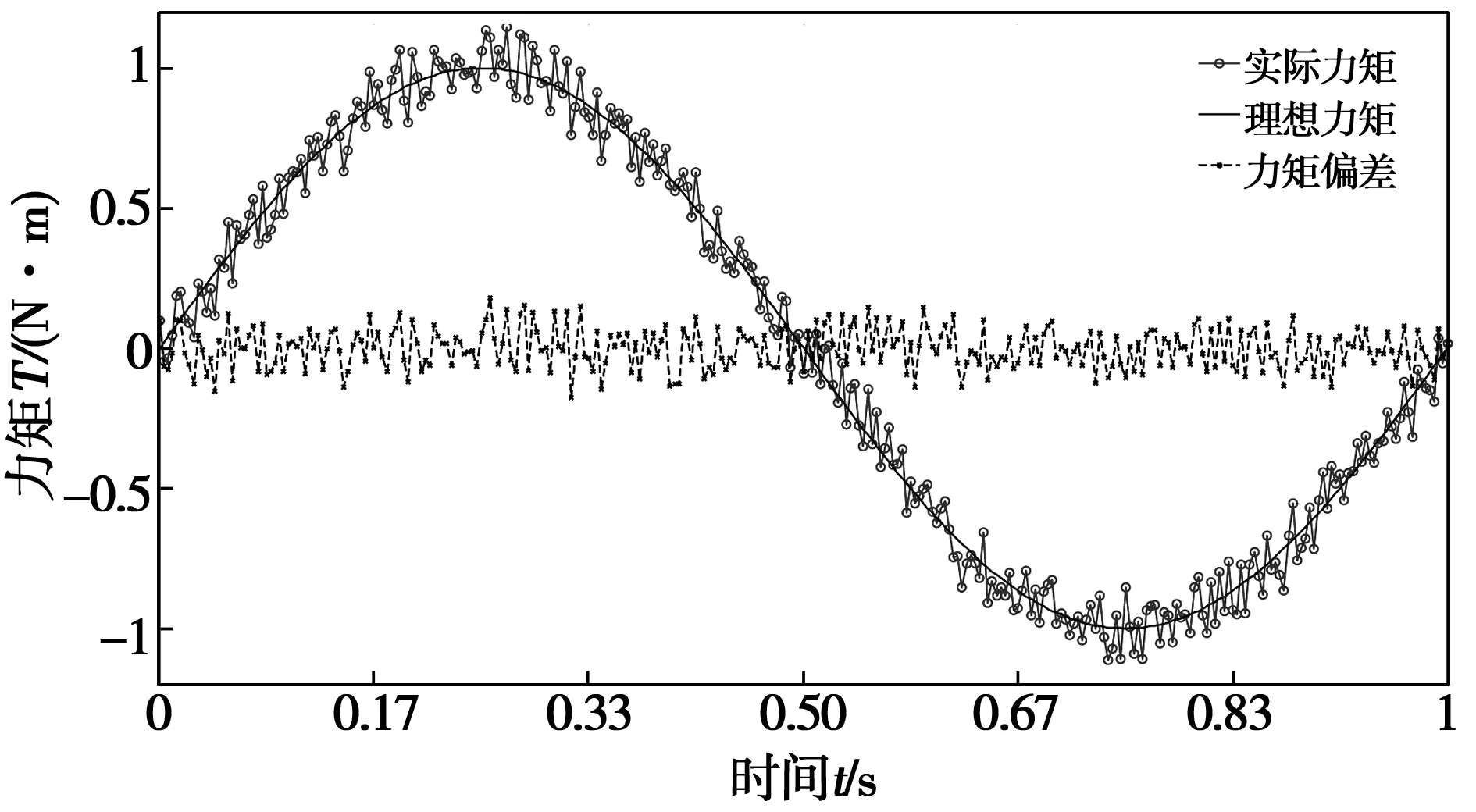
图7 输出力矩Td4=sin2πt实验曲线Fig.7 Curve of output torque with Td4=sin2πt

由图7可以知道，当负载电机匀速运动时，在力矩电机进入稳定工作状态后，输出力矩幅值越小，系统受外界干扰表现的更加突出，甚至某些时刻出现力矩偏差逼近9%，较幅值为2π的相对误差大1.3%，但相位滞后和大幅值基本相等。

综合上述提出的影响因素，为了更好的分析各种工作条件下系统性能的具体表现情况，分别采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)对实验结果进行评定[21]，如表2和表3所示。

表2 匀速工况下系统性能分析表Table 2 Analysis of the ELS in constant speed working conditions

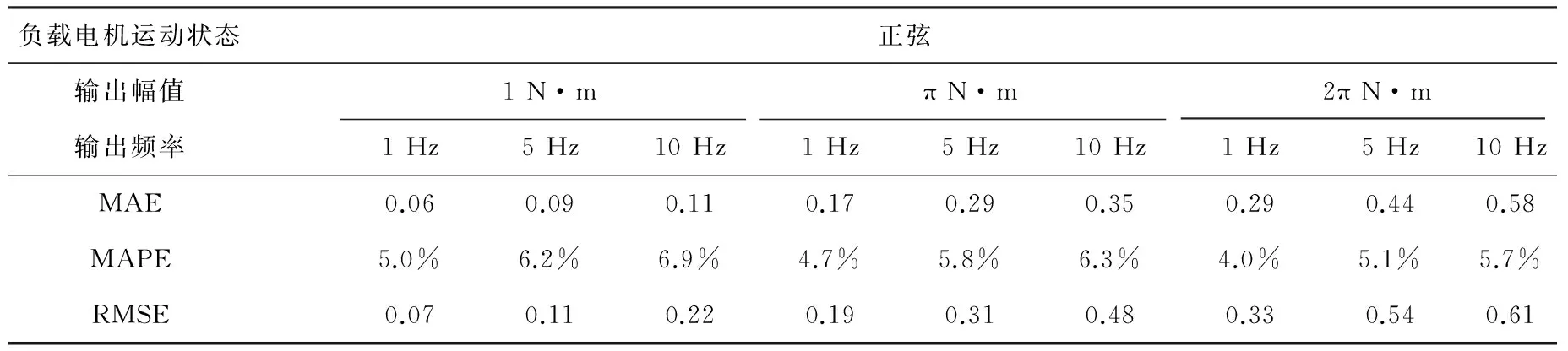
表3 正弦工况下系统性能分析表Table 3 Analysis of the ELS in sinusoidal speed working conditions

由表2具体实验数据可知，在力矩电机和负载电机耦合较小时，输出力矩幅值越大，频率越低，电动负载模拟器的控制性能更为优越。针对小幅值，高频率信号对系统性能的影响较大，为下一阶段的研究工作指明了方向，着重分析力矩传感器输出值和力矩电机输入力矩值等变量的关系，选择合适滤波和补偿方案，进一步提高系统的控制精确度和鲁棒性。

4 摩擦和间隙对系统性能的影响

摩擦和齿隙也是造成力矩畸变的主要非线性因素,摩擦是直接使力矩产生扰动,齿隙则是由于空程使力矩产生输出死区，所以两者对系统性能的影响因素也不同。由于电机本身及减速器等传动机构中存在着摩擦力，在温度、润滑和磨损等工作条件发生变化时摩擦力的实际情况更为复杂，特别是电机工作在低速阶段，摩擦力的变化对电动负载模拟器性能的影响尤为突出。LuGre摩擦模型广泛应用在负载模拟器系统中[20]，针对不同系统自身特点，建立动态的LuGre摩擦模型[11,21]，可以表示如下：

(3)

(4)

式中：σ0是鬃毛刚度系数；σ1是鬃毛阻尼系数；σ2是粘性摩擦系数；vr是瞬时相对速度；vs是Stribeck速度；z是鬃毛的平均变形量；μc是静摩擦系数；μs是最小动摩擦系数。分析上述摩擦情况可知，vr对摩擦力的影响较大，且受到运动方向等条件约束，具有不可逆转性，如图8所示。在设计系统结构时尽可能减小vr，以及各个接触面之间的摩擦损耗等。

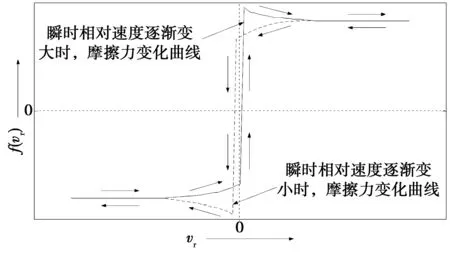
图8 摩擦力的不可逆转性Fig.8 Non-reversible characteristics of the friction force

电动负载模拟器中间隙的存在，必然会造成角位移误差，而齿隙模型作为补偿的工具广泛应用在传动系统的控制中。常用的齿隙模型主要有迟滞模型、死区模型和震冲模型3类，结合电动负载模拟器自身特点和相关典型模型，选取死区模型作为研究的重点[22-23]。死区模型的输入是相对角位移，输出两者之间的传递力矩，多用于诸如力矩控制系统中。针对该系统的特点，建立如下的死区模型

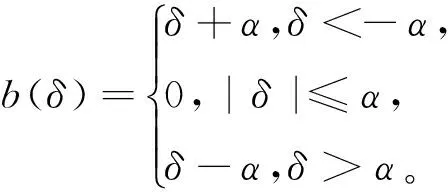
(5)

(6)

其中a>0、r>0为待定参数，为了分析其逼近死区函数的程度，定义两者的差值为

(7)

为了进一步分析摩擦和间隙对系统定性的影响，使得负载电机工作在匀速状态，负载模拟器工作在Td5=10sin10πt工况下，分别选取摩擦死区为[-0.5,0.5] N·m，间隙死区为[-0.001,0.001] rad，采样频率100 Hz。在两个死区独立存在时分析输出力矩和对应的傅里叶变换曲线，对比两者引起力矩谐波畸变的特点。

图9(a)中曲线较为平滑，图9(b)中曲线在上升沿波动较为剧烈，特别是在换向时干扰较大。从相应的FFT曲线分析可进一步得知图9(a)中谐波的主要成分为低次谐波，高频谐振峰处的谐波相对较小，图9(b)中谐波的主要成分在高次谐波，低次谐波较小。因此摩擦死区造成的谐波主要为低次谐波，而齿隙死区造成的谐波主要为高次谐波，在优化系统结构的同时，可以适当引入自适应的滤波器，进行带宽调节。

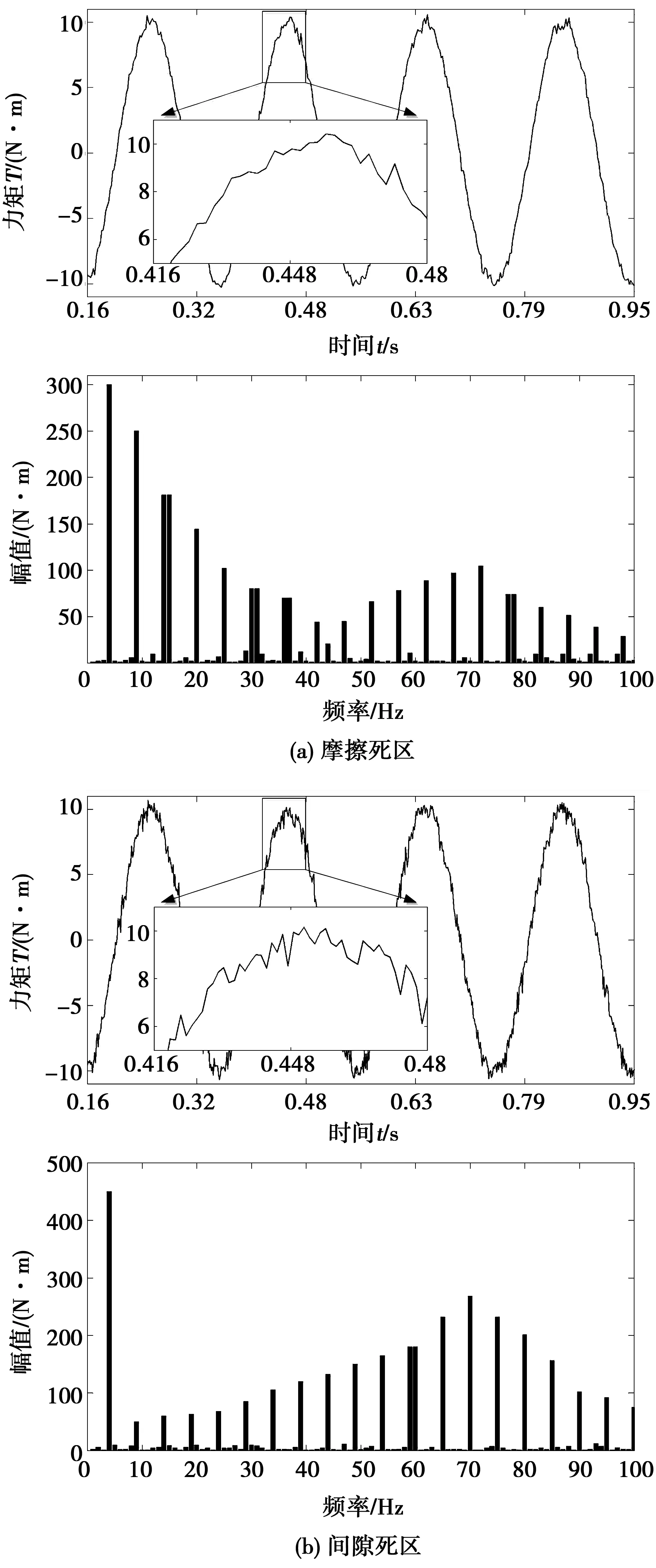
图9 摩擦死区和间隙死区对比Fig.9 Comparison between a friction dead zone and a backlash dead zone

5 结 论

以电动负载模拟器为研究对象，结合系统的自身特点，首先介绍了系统组成，然后建立了数学模型，最后详细研究了相关非线性因素对系统控制精确度和稳定性的影响：

1)选择合适的连接刚度，配以惯量盘组模拟火炮调转、发射时的惯性力矩，对输入力矩进行补偿修正，避免系统产生机械谐振；

2)负载电机运动越复杂，力矩电机的工作频率越大，幅值越小，系统的控制性能越差，但是均符合指标要求，反之则控制性能较好；

3)摩擦死区对系统的影响主要是低次谐波，而齿隙死区造成的影响主要为高次谐波，综合考虑系统结构和特性，可进一步提高传动系统和温度、润滑等工作条件，减小上述死区对系统性能的影响。

[1] DAO T L,DINH Q T,KYOUNG K A.A torque estimator using online tuning grey fuzzy PID for applications to torque-sensorless control of DC motors[J],Mechatronics,2015,26 (1): 45-63.

[2] WANG C W,JIAO Z X,LONG Q.Adaptive velocity synchronization compound control of electro-hydraulic load simulator[J],Aerospace Science and Technology,2015,42 (1): 309-321.

[3] 高强,候润明,杨国来，等.基于分数阶神经滑模的某顶置火炮调炮控制[J].兵工学报,2013,34(10),1311-1317. GAO Qiang,HOU Runmin,YANG Guolai,et al.Adjustment and Control of a Certain Top-mounted Gun Based on a Novel Fractional Order Neural Sliding Mode Strategy[J].Acta Armamentarll,2013,34(10): 1311-1317.

[4] SHANG Y X,YUAN H,JIAO Z X,et al.Matching design of hydraulic load simulator with aerocraft actuator,Chinese Journal of Aeronautics,2013,26(2):470-480.

[5] 慕香永,裴润,刘志林.用于船舶舵机的电液负载模拟器之控制系统[J].控制理论与应用,2008,25(3):564-568. MU Xiangyong,PEI Run,LIU Zhilin.A control system for the electro-hydraulic load-simulator employed in a marine rudder[J].Control Theory and Application,2008,25(3):564-568.

[6] 王力,钱林方,高强,等.基于灰预测模糊PID的随动系统负载模拟器力矩控制研究[J].兵工学报,2012,33(11): 1379- 1386. WANG Li,QIAN Linfang,GAO Qiang,et al.Research on torque control of servo system load simulator based on grey prediction fuzzy-PID controller [J].Acta Armamentarll,2012,33(11): 1379-1386.

[7] 王超,刘荣忠,侯远龙,等,基于新型小波神经网络和灰预测的电动负载模拟器控制[J].兵工学报,2014,35 (12): 1959-1966. WANG Chao,LIU Rongzhong,HOU Yuanlong,et al.Electric load simulator control based on a novel wavelet neural network and grey prediction[J].Acta Armamentarll,2014,35 (12): 1959-1966.

[8] 王鑫,冯冬竹.引入弹簧杆的电动负载模拟器实验研究[J].电机与控制学报,2012,16(9):91-94. WANG Xin,FENG Dongzhu.Experimental research on DC load simulator test bed with elastic rod[J].Electric Machines and Control,2012,16(9):91-94.

[9] 杜仁慧,吴益飞,陈威,等.考虑齿隙伺服系统的反步自适应模糊控制[J].控制理论与应用,2013(2):254-260. DU Renhui,WU Yifei,CHEN Wei,et al.Adaptive back- stepping fuzzy control for servo systems with backlash[J].Control Theory and Application,2013(2):254-260.

[10] 安凯.关节齿隙对空间机械臂末端定位精度的影响[J].兵工学报,2014,35(8):1301-1307. AN Kai.Effect of gear backlash on positioning precision of manipulator end-effectors[J].Acta Armamentarll,2014,35(8): 1301-1307.

[11] SAHA A,WAHI P.An analytical study of time-delayed control of friction- induced vibrations in a system with a dynamic friction model[J].International Journal of Non-Linear Mechanics,2014,63(1): 60-70.

[12] HAN S I,LEE J M.Adaptive dynamic surface control with sliding mode control and RWNN for robust positioning of a linear motion stage[J].Mechatronics,2012,22(2): 222-238.

[13] 王瑞娟,梅志千,李向国,等.机电伺服系统非线性摩擦自适应补偿的研究[J].中国电机工程学报,2012,32(36): 123-129. WANG Ruijuan,MEI Zhiqian,LI Xiangguo,et al.Research on Adaptive Nonlinear Friction Compensation of Mechatronic Servo Systems[J].Proceedings of the CSEE,2012,32(36): 123-129.

[14] CHEN M,ZHOU Y L,WILLIAM W.Robust tracking control for uncertain MIMO nonlinear systems with input saturation using RWNNDO [J].Neurocomputing,2014,144(1): 436- 447.

[15] MAHMOODABADIA M J,MOMENNEJADB S,BAGHERI A.Online optimal decoupled sliding mode control based on moving least squares and particle swarm optimization[J].Information Sciences,2014,268(1):342- 356.

[16] WANG F,LIU Z.LAI G Y.Fuzzy adaptive control of nonlinear uncertain plants with unknown dead zone output[J].Fuzzy Sets and Systems,2014,263:27-48.

[17] WANG C W,JIAO Z X,WU S,et al.A practical nonlinear robust control approach of electro-hydraulic load simulator[J].Chinese Journal of Aeronautics,2014,27(3):735-744.

[18] YAO J Y,JIAO Z X,YAO B.Robust control for static loading of electro-hydraulic load simulator with friction compensation[J].Chinese Journal of Aeronautics,2012,25(6): 954-962.

[19] DENG X S,WANG X Z.Incremental learning of dynamic fuzzy neural networks for accurate system modeling[J].Fuzzy Sets and Systems,2009,7(1):972-987.

[20] WIT C C,OLSSON H,ASTROM K J,et al.A new model for control of systems with friction[J],IEEE Transactions on Automatic Control,1995,40(1):419-425.

[21] MEZOUKI R,DAVILA J A,FRIDMAN L.Backlash phenomenon observation and identification in electromechanical systems [J].Control Engineering Practice,2007,15(4): 447- 457.

[22] ROCCA E,RUSSO R.The oretical and experimental investigation into the influence of the periodic backlash fluctuations on the gear rattle[J],Journal of Sound and Vibration,2011,330: 4738-4752.

[23] GIRI F,RADOUANE A,BROURI A,et al.Combined frequency-prediction error identification approach for Wiener systems with backlash and backlash- inverse operators[J],Automatica,2014,50: 768-783.

(编辑：贾志超)

Influence analysis on electric load simulator for the gun control system

WANG Chao， HOU Yuan-long， WANG Li， GAO Qiang， HOU Run-min

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210014,China)

In order to prevent the surplus torque existing in the electric load simulator (ELS) for gun control systems (GCS),and further improve the control precision and dynamic characteristics of the output torque,the study on the output torque influences of the ELS is put forward.First of all,based on the structure and working principle of the ELS system,a mathematical model was established,and the transfer function of output torque was obtained,with which influence factors were shown apparently.Then the connection stiffness,the input value of the torque motor,the angle of the position motor,friction,clearance and other nonlinear time-variant factors were studied in turn,and time-frequency and harmonic tracking methods were used to evaluate the system performance.At last,in combination with the results of simulation and experimental data,some qualitative and quantitative relationships of resulting in the harmonic distortion of the output torque were studied,which provides strong theoretical support for improving the control performance of the ELS.

electric load simulator; gun control systems; torque; nonlinearity; time-variant; harmonic distortion

2015-10-25

国家自然科学基金(51305205)

王 超(1989—)，男，博士研究生，研究方向为伺服系统控制、小波分析、人工智能等； 侯远龙(1964—)，男，教授，博士生导师，研究方向为多模态复合智能控制； 王 力(1977—)，男，博士，讲师，研究方向为伺服系统随动控制； 高 强(1979—)，男，博士，副研究员，研究方向为伺服系统随动控制； 侯润民(1987—)，男，博士，讲师，研究方向为伺服系统随动控制。

王 超

10.15938/j.emc.2016.12.010

TJ 819

:A

:1007-449X(2016)12-0074-08