北斗导航信号电离层闪烁模拟及其影响*

孙鹏跃，黄仰博，唐小妹，孙广富

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

北斗导航信号电离层闪烁模拟及其影响*

孙鹏跃，黄仰博，唐小妹，孙广富

(国防科技大学 电子科学与工程学院， 湖南 长沙 410073)

电离层闪烁具有突发性、偶发性和区域性，且难以建模准确刻画。针对电离层闪烁影响下的北斗导航信号复现问题，研究了基于应用伽马分布和零均值高斯分布模型的导航信号电离层闪烁序列生成方法，并基于国防科技大学电子科学与工程学院研制的NSS8000型多体制导航信号模拟器给出了北斗导航信号电离层闪烁模拟的硬件架构。在此基础上，通过中频信号采样和软件接收机处理，分析了电离层闪烁对北斗接收机跟踪环路的影响。结果表明：在相位闪烁指数为0，幅度闪烁指数为0.9时，码环鉴相误差可达0.05 chip；而在幅度闪烁指数为0，相位闪烁指数为0.5时，载波环鉴相误差可达15°，处于失锁的临界状态。

电离层闪烁；闪烁指数；导航信号模拟；跟踪环路；鉴相误差

电离层不均匀性会造成导航信号的绕射、聚焦和散射，形成电离层闪烁[1-2]，造成导航信号幅度和相位的快速变化，这不仅会增大接收机伪距和载波相位的测量误差，严重时还会造成单颗卫星信号的持续失锁[3-4]。当多颗卫星同时受到影响时，系统将失去导航服务功能。由于电离层闪烁的突发性、偶发性、区域性，且难以建模准确刻画，电离层闪烁影响下的GNSS导航信号很难复现，这为电离层闪烁减弱技术的研究带了很大难度。因此，电离层闪烁影响下的导航信号模拟仿真就显得尤为重要。

目前，国际上影响广泛的电离层闪烁模型主要有由Béniguel等在欧空局支持下提出的全球电离层闪烁模型(Global Ionospheric Scintillation Model，GISM)[5-6]、由美国政府支持的NWRA研究组提出的宽带电离层闪烁模型(Wide Band ionospheric scintillation MODel， WBMOD)[7]以及由Cornell大学研发的康奈尔闪烁模型(Cornell Scintillation Model， CSM)[8]。不同模型各有特点，研究人员利用这些模型进行了大量研究，Julien等[9]提出了一种包含电离层闪烁影响的GPS软件信号模拟器；Ghafoori等[10]提出了一种基于Spirent GSS7700信号模拟器的GPS导航信号电离层闪烁仿真技术；寇艳红等[11-12]对集成电离层闪烁模型的数字中频GPS信号模拟器进行设计验证。可以看出，目前国内外电离层闪烁影响下的导航信号仿真数据生成研究主要集中在GPS系统，并且均局限于软件仿真或设计验证阶段，尚无电离层闪烁影响下的北斗导航信号高精度模拟及其北斗接收机跟踪环路性能分析的研究。

1 电离层闪烁模型

电离层闪烁会引起GNSS信号幅度和相位的快速波动，接收机收到的信号为：

r(t)=A0·δA·C(t-τ)D(t-τ)cos(ωt+φ0+δφ)+n(t)

(1)

其中：A0为信号幅度，C(t)为扩频码，D(t)为电文序列，ω为载波频率，φ0为初始相位，n(t)为噪声，δA和δφ分别为电离层闪烁引起的幅度和相位波动。

电离层闪烁的强度一般采用幅度闪烁指数S4和相位闪烁指数σφ来表征，S4定义为归一化的信号强度标准差。

(2)

其中：I=A2=(A0·δA)2为信号强度。

相位闪烁指数定义为载波相位的标准差。

(3)

其中：φ=φ0+δφ为载波相位。

文献[1]研究表明，电离层闪烁引起的GNSS信号幅度闪烁符合Nakagami-m分布，而相位闪烁服从Gaussian分布，这为电离层闪烁序列的模拟提供了理论基础。Nakagami-m分布的概率密度函数为：

(4)

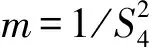
从图1中可以看出，S4趋近于0时，功率波动集中在1附近，近似于正态分布，对信号功率波动影响较小；随着S4增大，功率波动小于1的值增多，表示电离层闪烁引起接收信号幅度衰落越来越大。而当σφ比较小时，载波相位波动集中在0附近，对信号相位波动影响较小，随着σφ增大，载波相位波动不为0的值增多，相位波动越来越大。

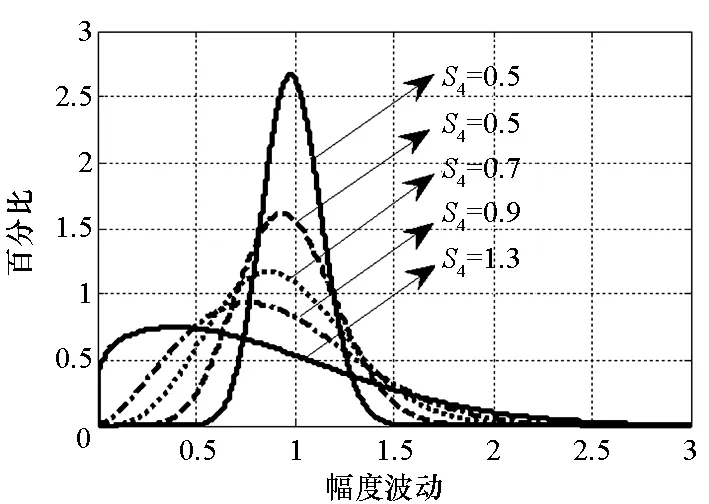
(a) 幅度闪烁概率分布(a) Distribution of signal amplitude scintillation

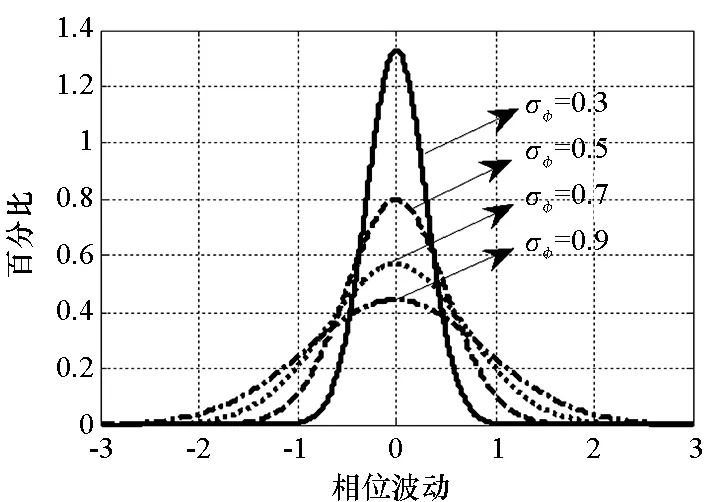
(b) 相位闪烁概率分布(b) Distribution of signal phase scintillation图1 不同强度闪烁下，信号幅度和相位概率分布Fig.1 Distribution of signal amplitude and phase under different ionospheric scintillation

2 北斗导航信号闪烁模拟

2.1 闪烁序列生成

由式(1)可知，幅度闪烁和相位闪烁分别以乘性和加性规律叠加在导航信号中，要模拟电离层闪烁影响下的GNSS导航信号，首先需要模拟产生电离层幅度和相位闪烁序列。由于工程上直接产生服从Nakagami-m分布的随机序列难以实现，而产生Γ(α,β)分布的随机序列比较成熟。因此，研究了基于Γ(α,β)分布产生GNSS信号幅度闪烁序列的方法，Γ(α,β)分布的概率密度函数为：

(5)

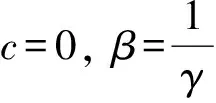
(6)

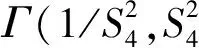
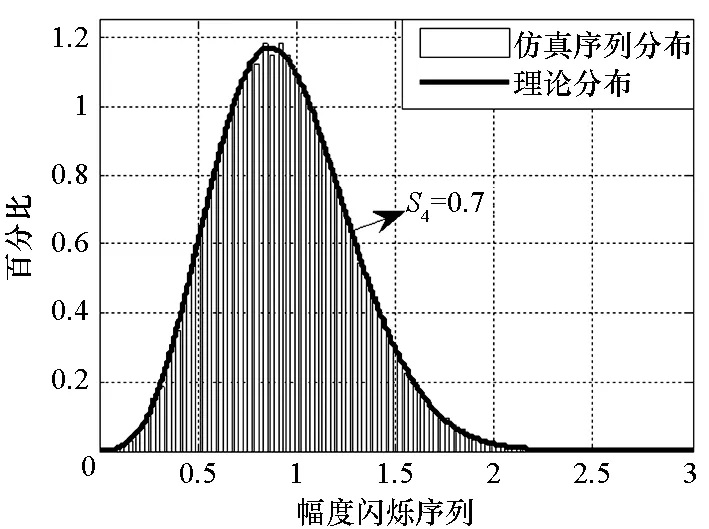
(a) 幅度闪烁序列统计特性(a) Statistical distribution of amplitude time-series

(b) 相位闪烁序列统计特性(b) Statistical distribution of phase time-series图2 仿真产生的幅度和相位闪烁序列的统计特性Fig.2 Statistical distribution of simulated amplitude and phase time-series

2.2 北斗闪烁信号模拟

基于本单位研制的NSS8000型多体制导航信号模拟器，给出了电离层闪烁影响下的北斗导航信号模拟的硬件实现，算法的具体架构如图3所示。

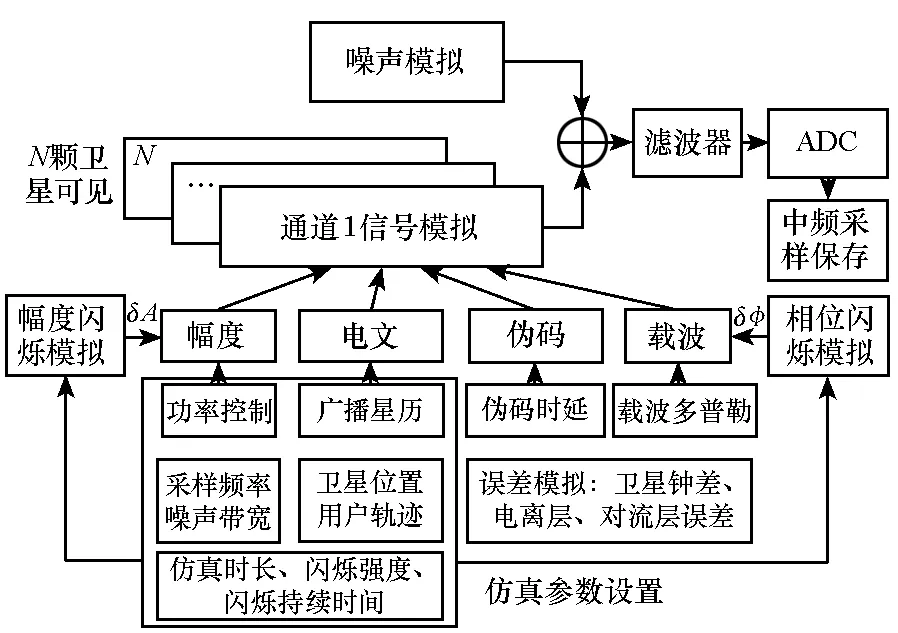
图3 北斗电离层闪烁信号模拟架构Fig.3 Simulation architecture of BeiDou signal in presence of ionospheric scintillation

电离层闪烁影响下的北斗导航信号生成主要包含仿真控制子系统和信号生成子系统。仿真控制子系统由外置的高性能PC机实现，主要完成导航信号模拟的相关参数的生成，包括电离层闪烁序列生成、功率控制参数生成、导航电文组帧和伪码以及载波控制参数计算等。这些参数通过千兆以太网分发给信号生成子系统的各个板卡和模块。信号生成子系统是导航信号模拟的硬件部分，以板卡式结构实现多系统、多频点导航信号的生成。主要包含工控机、多个信号处理板卡、时频板卡以及显控模块等。

之后，通过高速示波器对中频信号进行采样，并通过软件接收机对信号幅度和相位闪烁特性进行验证。信号中频频率为9.548 MHz，采样频率为38.192 MHz，同时仿真3颗卫星，每分钟保持相同闪烁强度，NSS8000信号模拟器设置见表1。

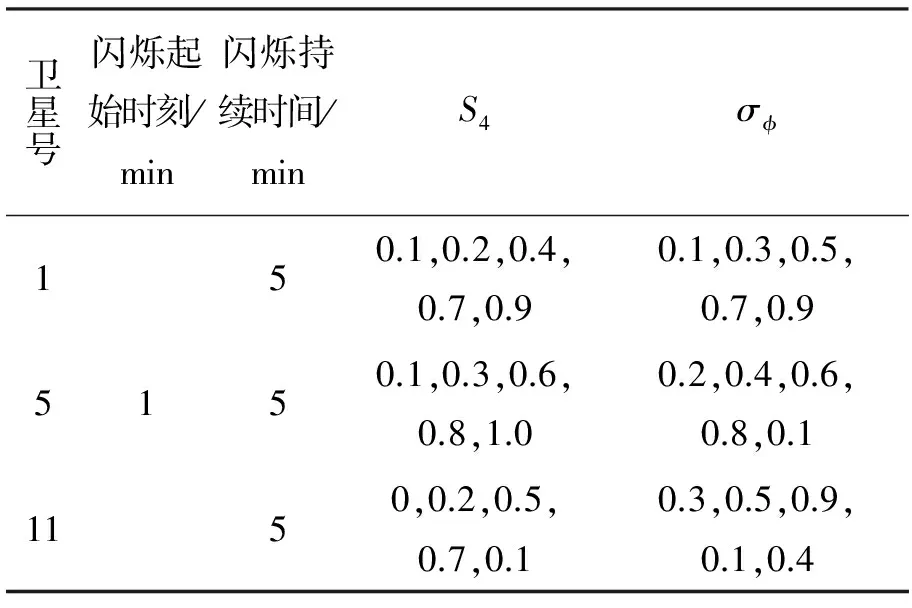
表1 北斗B1信号电离层闪烁参数设置Tab.1 BeiDou B1 signal ionospheric scintillation parameter settings

采用本单位研制的北斗软件接收机，对高速示波器采样的中频信号进行处理，卫星1信号幅度和相位波动特性见表2。

表2仅给出了卫星1的幅度和相位波动，从中可以看出，随着幅度和相位闪烁指数的增大，信号的幅度和相位波动也随之变得剧烈。

对信号进行消趋势处理后，计算幅度和相位闪烁指数，结果如图4所示。

表2 北斗B1信号幅度和相位波动特性Tab.2 Fluctuation of BeiDou B1 signal amplitude and phase

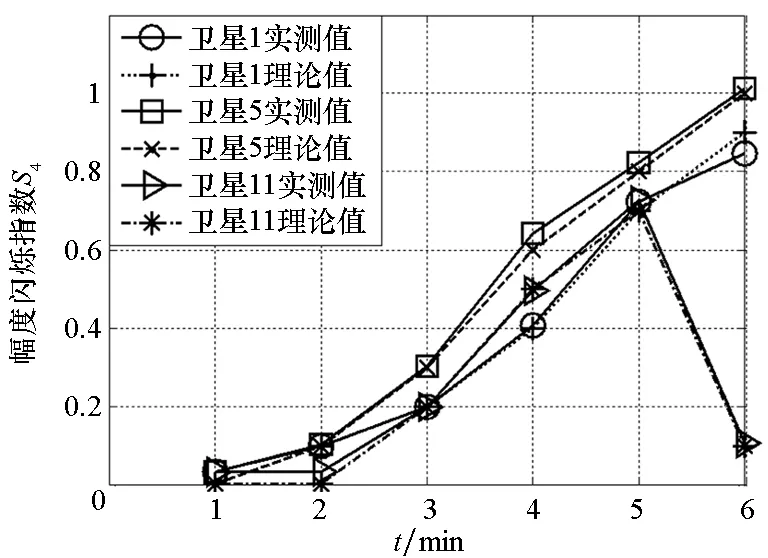
(a) 信号幅度闪烁指数(a) Signal amplitude scintillation index

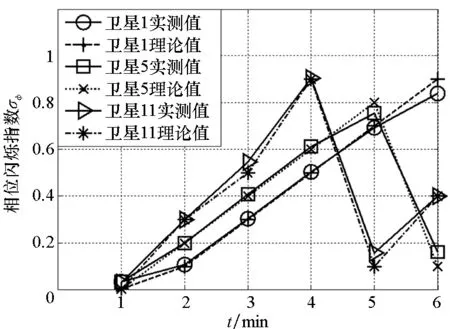
(b) 信号相位闪烁指数(b) Signal phase scintillation index图4 北斗B1信号幅度和相位闪烁指数验证Fig.4 BeiDou B1 signal amplitude and phase scintillation index

可以看到，通过信号幅度和载波相位的采样数据计算得到的幅度和相位闪烁指数，与仿真设定值相吻合，这也充分验证了电离层闪烁信号模拟方法。

3 跟踪环路性能分析

在正确模拟电离层闪烁影响下的导航信号的基础上，对不同闪烁强度下北斗接收机跟踪环路的性能进行分析。在电离层闪烁影响下，相位锁定环路(Phase Lock Loop， PLL)相位抖动均方差[13-14]为：

(7)

其中，σφ为相位闪烁均方差，σT为热噪声均方差，σOSC为晶振噪声均方差，各个分量的计算公式此处不再赘述。PLL的1σ经验门限[15]为：

σPLL≤15°

(8)

对于延迟锁定环路(Delay Lock Loop， DLL)而言，其鉴相误差均方差[15]为：

(9)

其中：BL为环路噪声带宽；Tcoh为相干积分时间；D=2d，d为相关器间距；C/N0为信号载噪比。DLL的1σ经验门限[15]为：

(10)

为了确保PLL和DLL在不同强度电离层闪烁下均能正常跟踪，仿真过程中北斗软件接收机环路参数设置见表3。

表3 北斗软件接收机参数设置Tab.3 BeiDou software receiver settings

对PLL环路性能进行分析，电离层相位闪烁以步进0.05从0增加到1遍历设置；而幅度闪烁设置4种状态，分别为无、弱、中等以及强幅度闪烁(S4=0，0.2,0.5,0.9)，将幅度和相位闪烁指数进行组合，则有80种不同强度的电离层闪烁场景。针对每一种闪烁场景，仿真生成1 min的导航信号，利用高速示波器采样中频信号，并将原始信号保存为二进制文件。通过软件接收机处理保存的中频信号，计算每分钟内PLL鉴相误差的标准差，则可以得到不同电离层闪烁强度下接收机PLL的环路性能。

采用软件接收机仿真验证PLL的环路性能，可直接对每分钟PLL的鉴相误差进行统计分析，计算得到其标准差。令PLL鉴相误差序列为φe={φe(1),φe(2),…,φe(N)}，其中N=60 000为每分钟的鉴相误差序列长度，则鉴相误差标准差为：

(11)

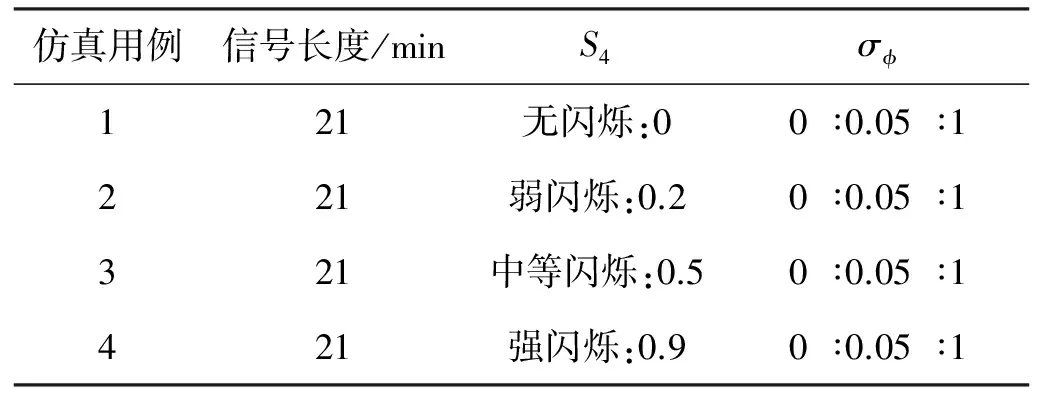
表4 北斗B1频点电离层闪烁参数遍历设置(PLL)Tab.4 BeiDou B1 signal ionospheric scintillation parameter ergodic settings(PLL)

PLL环路性能仿真结果如图5所示。

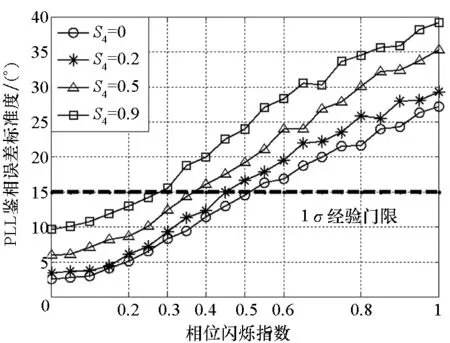
图5 不同电离层闪烁强度下PLL性能分析Fig.5 Performance analysis of PLL under different ionospheric scintillation

可以看到， PLL相位颤动随着相位闪烁指数的增大急剧增强，在无幅度闪烁情况下，当σφ=0.5时，PLL鉴相误差标准差已达1σ经验门限。由式(8)可知，此时PLL已处于失锁的临界状态，当σφ=1时，PLL相位颤动可达28°， PLL相位颤动严重超出牵入范围。另外，PLL鉴相误差对幅度闪烁指数也比较敏感，可以看到，随着幅度闪烁指数的增大，PLL鉴相误差标准差也随之增大。在强幅度闪烁(S4=0.9)下，仅当σφ=0.3时，PLL鉴相误差标准差就达到1σ经验门限。

对DLL环路性能进行仿真分析，电离层幅度闪烁以步进0.045从0增加到0.9遍历设置；而相位闪烁设置4种状态，分别为无、弱、中等以及强幅度闪烁(σφ=0，0.3,0.6,1)，组合后同样有80中不同场景。采用类似的分析算法，计算DLL的鉴相误差标准差，NSS8000模拟器电离层闪烁参数设置见表5。

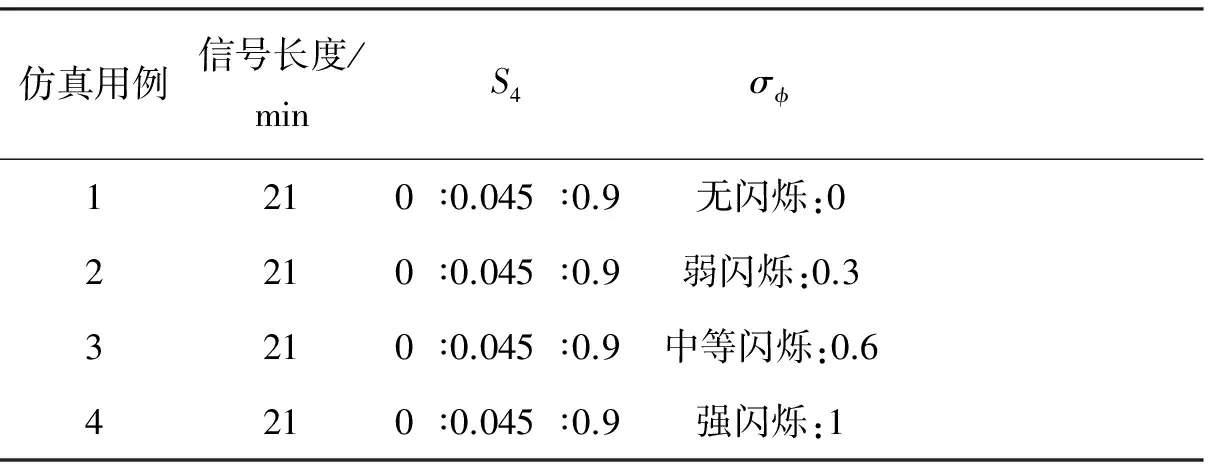
表5 北斗B1频点电离层闪烁参数遍历设置(DLL)Tab.5 BeiDou B1 signal ionospheric scintillation parameter ergodic settings(DLL)

DLL环路性能仿真结果如图6所示。

图6 不同电离层闪烁强度下DLL性能分析Fig.6 Performance analysis of DLL under different ionospheric scintillation

可以看到，当相位闪烁不强时，DLL相位颤动对相位闪烁指数变化并不敏感，而随着幅度闪烁指数的增大急剧增强。在无相位闪烁的情况下，当幅度闪烁指数S4=0.9时，DLL鉴相误差标准差可达0.05 chip。但当相位闪烁指数σφ=1时，DLL鉴相误差明显增大，当S4=0.9时，DLL鉴相误差标准差可达0.07 chip，但仍未达到DLL的1σ经验门限。

4 结论

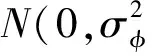
References)

[1] Yeh K C, Liu C H. Radio wave scintillations in the ionosphere[J]. Proceedings of the IEEE, 1982, 70(4): 324-360.

[2] Crane R K. Ionospheric scintillation[J]. Proceedings of the IEEE, 1977， 65(2): 180-199.

[3] Kintner P M, Ledvina B M, de Paula E R. GPS and ionospheric scintillations[J]. Space Weather, 2007, 5(9): 83-104.

[4] Hegarty C, El-Arini M B, Kim T, et al. Scintillation modeling for GPS-wide area augmentation system receivers[J]. Radio Science, 2001, 36(5): 1221-1231.

[5] Béniguel Y. Global ionospheric propagation model(GIM)：a global ionospheric propagation model for scintillations of transmitted signals[J]. Radio Science, 2002, 37(3): 1032-1044.

[6] Béniguel Y, Adam J P, Jakowski N, et al. Analysis of scintillation recorded during the PRIS measurement campaign[J]. Radio Science, 2009, 44(5): 1-10.

[7] Fremouw E J, Secan J A. Modeling and scientific application of scintillation results[J]. Radio Science, 1984, 19(3): 687-694.

[8] Humphreys T E, Psiaki M L, Hinks J, et al. Simulation ionosphere-induced scintillation for testing GPS receiver phase tracking loops[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(4): 707-715.

[9] Julien O, Zheng B, Dong L, et al. A complete software-based IF GNSS signal generator for software receiver development[C]//Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2004.

[10] Ghafoori F, Skone S. GPS scintillation modeling and receiver design strategies for low-latitude regions[C]// Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2014.

[11] Kou Y H, Zhou X Y, Yu M, et al. Processing GPS L2C signals under ionospheric scintillation[C]//Proceeding of Position Location and Navigation Symposium, 2010: 771-782.

[12] 王娜, 寇艳红. 集成电离层闪烁仿真的数字中频GPS信号模拟器设计验证[J]. 导航定位学报, 2014, 2(1): 55-61. WANG Na, KOU Yanhong. Design and validation of a digital IF GPS signal simulator capable of ionospheric simulation[J]. Journal of Navigation and Positioning, 2014, 2(1): 55-61.(in Chinese)

[13] Conker R S, El-Arini M B, Hegarty C J, et al. Modeling the effects of ionospheric scintillation on GPS/satellite-based augmentation system availability[J]. Radio Science, 2003, 38(1): 1-23.

[14] Todd E H, Mark L P, Pual M K, et al. Modeling the effects of ionospheric scintillation on GPS carrier phase tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1624-1637.

[15] Kaplan E D, Hegarty C J. GPS原理与应用[M]. 2版. 北京: 电子工业出版社, 2007. Kaplan E D, Hegarty C J.Understanding GPS: principles and applications[M]. 2nd ed.Beijing: Electronic Industry Press， 2007. (in Chinese)

Simulating and analyzing the impact of ionospheric scintillation for BeiDou navigation signals

SUN Pengyue, HUANG Yangbo, TANG Xiaomei, SUN Guangfu

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Due to its accidental, sudden and regional characteristics, the simulation of GNSS navigation signals under ionospheric scintillation is difficult to be implemented accurately. The ionospheric scintillation time-series generation method based on Gamma distribution and zero-mean Gaussian distribution was proposed. With the NSS8000, a multi-system navigation signal simulator developed by our department, the hardware architecture of BeiDou navigation signal simulation under ionospheric scintillation was given. Then based on this, by intermediate frequency signal sampling and software receiver processing, the impact of ionospheric scintillation on BeiDou receiver tracking loops was analyzed. The results indicate that the code tracking error can reach 0.05 chips when the phase scintillation index is 0 and amplitude scintillation index is 0.9, while the carrier tracking error can reach 15 degrees when the amplitude scintillation index is 0 and the phase scintillation index is only 0.5, which the carrier tracking loops is almost loss of lock.

ionospheric scintillation; scintillation index; navigation signal simulation; tracking loops; discriminator error

10.11887/j.cn.201606018

2015-05-23

国家自然科学基金资助项目(61403413)

孙鹏跃(1988—)，男，陕西咸阳人，博士研究生，E-mail：sunnnpy@163.com; 孙广富(通信作者)，男，研究员，博士，博士生导师，E-mail：sunguangfu_nnc@163.com

P352

A

1001-2486(2016)06-111-06

http://journal.nudt.edu.cn