压缩感知稀疏重构对星图的影响*
2017-01-07尹航,闫野,宋新
尹 航,闫 野,宋 新
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
压缩感知稀疏重构对星图的影响*
尹 航,闫 野,宋 新
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
稀疏重构是压缩感知理论的核心内容之一,为了将稀疏重构有效地应用于星敏感器的压缩成像过程中,从星图图像误差和星点特征误差两个方面分析稀疏重构对星图的影响。在图像误差方面,利用峰值信噪比评价指标考察星图在不同重构算法、不同压缩比下的重构质量;在特征误差方面,从理论上分析稀疏重构对星点特征的影响机理,提出星点特征重构误差的评价指标,考察星点的质心、亮度和数量特征的重构误差。结果表明,在所选算法各压缩比下,星图相比一般图像能够获得更高的重构质量,重构星点能够在很大程度上保持可用于姿态确定的特征信息,结论保证了利用重构星图进行姿态计算的正确性,进一步验证了压缩感知理论在星敏感器中应用的可行性,为实现星敏感器的压缩成像提供了现实依据。
压缩感知;稀疏重构;恒星敏感器;恒星图像
星敏感器是当前航天器中广泛采用的一种高精度、高可靠性的姿态测量部件。其基本原理为利用电荷耦合器件(Charged Coupled Device, CCD)或互补金属氧化物半导体(Complementary Metal-Oxide-Semiconductor transistor, CMOS)图像传感器对当前视场内的星空进行成像,通过信号处理提取星点在观测视场中的特征信息(如位置、亮度和数量等),由星模式识别算法在导航星库中找到观测星的对应匹配,从而计算出星敏感器的三轴姿态。随着航天任务对姿态测量与控制精度要求的不断提高,星敏感器也向着大视场、高精度和高动态方向发展,需要其图像传感器具有更高的像素分辨率。然而,提升分辨率意味着减少传感器像素尺寸、增加阵元数量,这不仅增加了系统的复杂度和实现难度,而且会造成星敏感器采样数据量过大以及处理速度不足等问题[1],对其效能及应用造成较大的限制。
压缩感知[2-3](Compressive Sensing, CS)是一种新型的信息理论,该理论基于信号的稀疏性,利用少量非相关的线性测量,对信号同时进行采样和压缩编码,最终通过稀疏重构算法实现信号的高精度重构。在光学成像领域[4-5],该理论提供了一种全新的图像获取方式,通过低数据率采样获得与传统成像体制相当甚至更高质量(如分辨率、信噪比等)的图像。因此,将压缩感知应用到星敏感器的成像过程中,利用少量的采样数据重构与原始星图质量相当的图像,对于解决在传统Nyquist采样定理下星敏感器进一步提高分辨率遇到的问题具有重要的意义。
当前,压缩感知理论主要包括信号的稀疏表示、非相干测量和稀疏重构三方面内容。稀疏重构是压缩感知理论的核心,也是压缩感知得以实现的保证,即要保证重构的信号能够最大限度地接近原始信号,从而满足实际应用需求。理论上,稀疏重构算法能够在概率意义上实现信号的精确重构或者在一定误差下的近似重构[3],而实际中,受重构算法计算精度和收敛速度等因素影响,重构信号与原始信号之间往往存在不同程度的误差。
一般地,光学压缩成像(如遥感压缩成像[6-7])通常利用图像重构前后的宏观差异衡量图像的重构质量,常用的指标包括峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)或均方根误差(Root Mean Square Error, RMSE)等。星图是一类特殊的图像,只有少量的像素记录了星点或噪声信息,其余大部分像素均未包含任何信息,星点的局部特征是星识别的唯一有效信息。研究中发现,稀疏重构不仅会造成星图的图像误差,而且会在一定程度上影响星点的局部特征,主要表现为星点质心位置的偏移、亮度的改变和产生干扰星影响。
针对压缩感知理论的前两个方面,结合星敏感器的应用,本文在以往的研究中对星图的稀疏性进行了分析[8],提出了一种适用于星敏感器压缩成像的测量矩阵[9]。本文为第三方面——稀疏重构的研究,针对星图特点,从星图图像误差和星点特征误差两个方面定量考察了压缩感知稀疏重构对星图的影响。
1 基本理论
1.1 压缩感知理论
(1)
即:
x=Ψ·α
(2)
其中Ψ=[ψ1,ψ2,…,ψN]是N中的一组表示基,α=[α1,α2,…,αN]T是信号x在对应表示基上展开的系数向量。如果信号x可以用K个基向量的线性组合来近似表示,即系数向量α中仅有K个较大非零元素,则称x是K阶稀疏信号。
压缩感知的采样过程在数学上描述为利用一个M维测量矩阵Φ将N维K阶稀疏信号x投影到低维空间上,得到M维的测量值向量y∈M,其中M≪N,即:
y=Φx=ΦΨα=Θα
(3)
其中Θ为测量矩阵和表示基组成的复合矩阵,称为感知矩阵[10]。基于信号的稀疏先验条件,压缩感知通过稀疏重构完成由低维观测向量y向N维原始信号x恢复的过程。理论上,如果感知矩阵Θ满足约束等距性质(Restricted Isometry Principle,RIP),信号x就能够以很高的概率从观测值y中重构,即对于任意K阶系数向量α,存在常数δk∈(0,1)使得矩阵Θ满足:
(4)
这样,通过求解一个稀疏约束下的优化问题,可以恢复出稀疏系数向量α,进而由式(2)计算得到重构信号。
对此,学者们提出了许多解决该问题的重构算法,一般形式上,主要分为凸优化算法和贪婪算法两个大类。凸优化算法[11]是将l0范数的非凸组合优化问题转化为l1范数的凸松弛问题,针对l1范数最小进行求解,其求解模型为:
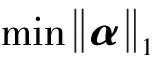
(5)
贪婪算法[12]基于匹配追踪的思想,通过局部最优化依次找到系数向量中的各个非零元素,其求解模型为:
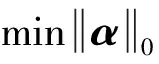
(6)
比较而言,凸优化算法重构精度高,但计算量大、重构时间长;而贪婪算法计算量小、重构速度快,但重构精度稍差。本文在以上两类算法中各选取两种较为典型的方法,考察稀疏重构过程对星图图像质量和星点局部特征的影响。其中凸优化算法选择内点法(Interior Point Method, IPM)[13]和梯度投影法(Gradient Projection for Sparse Reconstruction, GPSR)[14],贪婪算法选择正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)[15]和压缩采样匹配追踪算法(Compressive Sampling Matching Pursuit, CoSaMP)[16]。需要说明的是,本文的研究重点不是重构算法本身,而是利用不同算法对比分析星图图像和星点特征的重构效果。
1.2 传统图像重构误差评价
在压缩感知成像应用中,传统上采用PSNR或RMSE作为评价整幅图像重构误差的指标,二者作用基本一致,主要从整体上反映了重构图像对原始图像的逼近程度。以PSNR评价为例,其定义过程为:
(7)
可见,PSNR值越大,重构图像就越接近原始图像。
然而,星图中的背景占据了绝大多数像素并且不包含有效信息,星点像素占有量虽然较少却包含着星识别的关键信息。这样,传统的重构误差评价指标(如PSNR)只能够反映星图图像的重构质量,难以准确评价星点特征的重构效果。因此,需要通过进一步分析稀疏重构对星点特征的影响,从而提出星点特征重构误差的指标。
2 星图特征重构误差评价
2.1 误差分析
一般地,星图的特征主要是指图像中星点的质心位置、亮度和数量。在星识别中,星点的误差因素主要表现为位置误差、亮度误差和干扰星影响三个方面[17]。其中干扰星包括伪星和缺失星,伪星指在星图中被误提取出来而在星表中不存在的“星点”,缺失星指由于噪声等原因未能成功提取的星点。理论上,稀疏重构对星图的影响本质是像素值的变化,这种变化在导致图像误差的同时也造成了星点特征误差,主要表现为:①星点亮度的变化;②星点质心位置的偏移;③干扰星的产生。图1举例说明了稀疏重构对星点特征的影响。
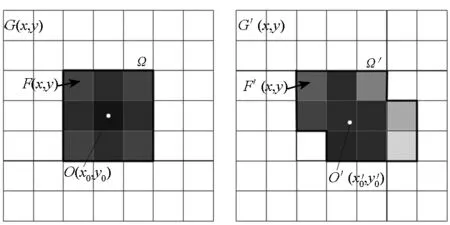
(a) 原始星点 (a) Original star (b) 重构星点 (b) Reconstructed star图1 稀疏重构对星点影响示意图Fig.1 Illustration of the effect of sparse reconstruction on star
设原始星图各像素值为f(x,y),其中包含一个理想高斯星点作为原始星点,如图1(a)所示。定义原始星点区域为Ω,则星点像素值F(x,y)和背景像素值G(x,y)分别可以表示为:
F(x,y)=f(x,y), (x,y)∈Ω
(8)
G(x,y)=f(x,y), (x,y)∉Ω
(9)
由此,根据质心法[18]计算得到的原始星点质心位置O(x0,y0)即为:
(10)
同样地,定义重构星图各像素值为f′(x,y),重构星点区域为Ω′,如图1(b)所示,对于重构后星点像素值F′(x,y)和背景像素值G′(x,y)分别有:
F′(x,y)=f′(x,y), (x,y)∈Ω′
(11)
G′(x,y)=f′(x,y), (x,y)∉Ω′
(12)
理论上,在同等提取条件下,重构过程中星点像素值和背景像素值的变化会在一定程度上改变星点区域,即一些星点像素值重构后可能低于背景阈值而被划分为背景像素,而一些背景像素值重构后由于高于背景阈值被划分为星点像素,使得Ω′与Ω表示了不同的区域,图1示意了这种差别。特殊情况下,这种变化可能使得暗星在重构后大部分像素值低于背景阈值,从而导致提取失败形成缺失星,或者一些连通背景像素高于背景阈值而被错误提取为伪星。此外,由式(10)可见,星点质心位置O(x0,y0)与星点像素值F(x,y)及星点区域Ω有关,由于稀疏重构对F(x,y)及Ω均会产生影响,因此也必然会造成星点质心位置的偏移。
2.2 评价指标
分别从质心偏移、星点区域亮度变化和干扰星影响三个方面对星点特征重构误差进行评价。首先,通过重构星点相对原始星点的质心偏移量对星点质心的位置误差进行评价。考虑原始星点质心O与重构星点质心O′在图像上的距离D为:
(13)
一般来讲,大部分星识别算法均可以承受至少一个像素以内的质心位置误差,因此若重构星点的质心偏移量保持在这个范围内,则可认为该星点在重构过程中成功保持了质心位置,否则认为其未能成功保持质心位置。通过统计重构星图中满足以上条件的星点比例,定义为质心重构成功率,评价稀疏重构对星点质心特征的影响。
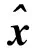
(14)
同时,为了能够与整幅图像PSNR作对比分析,定义背景区域PSNR为:
(15)
再次,对稀疏重构过程中产生的干扰星影响进行评价。定义原始星点为Si(i=1,2,…,N),重构星点为Ti(i=1,2,…,N′),其中N和N′分别表示重构前后图像中星点数量。对比重构前后星图,若在Si的一定邻域内无法找到相应的重构星点,则将其判定为缺失星;反之,若在Ti的邻域内找不到原始星点,则将其判定为伪星。设星图重构过程中缺失星数量为Nm、伪星数量为Ns,考察二者在星图中各自所占的比例Nm/N和Ns/N,由此对干扰星影响进行评价。
3 仿真分析
3.1 星图图像重构误差
考察选定的四种重构算法在不同压缩比(测量次数M与原始图像维数N的比值)下对星图图像的重构误差。选择离散余弦变换(Discrete Cosine Transform, DCT)基作为稀疏表示基、加权分块循环矩阵[9](Weight Block Circulant Matrix, WBCM)作为测量矩阵,若无特殊说明,本文均采用以上重构条件。仿真数据选取99幅分辨率为512×512的地面观测星图构成的图像库,其包括在相同成像参数下对不同方位星空的成像结果,在实验中具有一定的可比性和代表性。仿真中,对每幅星图分别选取20%,40%,60%和80%压缩比进行稀疏重构,分别得到IPM,GPSR,OMP和CoSaMP四种重构算法在不同压缩比下的图像重构误差。在图像库中,分别统计同一类重构算法中不同压缩比下的PSNR值,并按降序排列进行比较,统计结果如图2所示。
由图2可见,在相同的算法下,压缩比与重构质量成正比,即通过较多测量数据能够得到更加接近原始图像的结果,这符合稀疏重构理论的一般规律。结果表明,同一种算法在四种不同压缩比下对星图的重构质量较为接近,即压缩比每提升20%时,PSNR平均值增加2dB以内。这是因为星图图像内容较为单一,其中大部分像素均为黑色背景,相比一般场景图像[4,7],星图在较低的压缩比(如20%)下即能够获得较好的整体重构质量,进一步提高压缩比对提升星图图像重构质量较为有限。需要说明的是,不同图像在相同重构条件下PSNR值表现出一定的差别,其原因主要有以下两点:首先,由于暗星图像的重构质量低于亮星图像,表现为星点区域和像素灰度值的变化两方面,这使得含有暗星较多的星图理论上具有更大的重构误差;其次,星图的背景并不是理想情况下灰度值为零,而是在图像背景中随机分布的低灰度值的像素,星图之间在背景像素方面本身存在着差异,其在原始图像中表现较不明显,但这种差别在重构过程中则会导致不同程度的重构误差。
对比四种不同的重构方法,凸优化算法(IPM和GPSR)对星图的重构质量整体上优于贪婪算法(OMP和CoSaMP)。其中IPM算法重构精度最佳,GPSR算法重构精度接近IPM算法,在各压缩比下PSNR平均值比IPM算法低0.3~0.7 dB;OMP算法重构精度最低,其改进算法CoSaMP在各压缩比下PSNR平均值比OMP算法高0.6~1.4 dB。
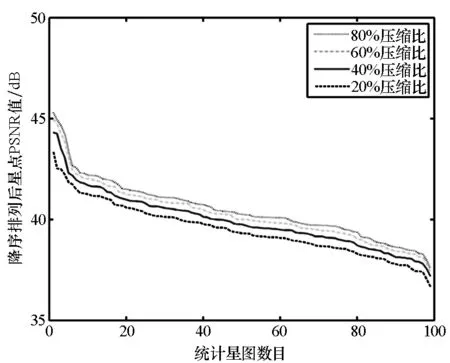
(a) IPM算法稀疏重构图像PSNR(a) PSNR of sparse reconstruction by IPM
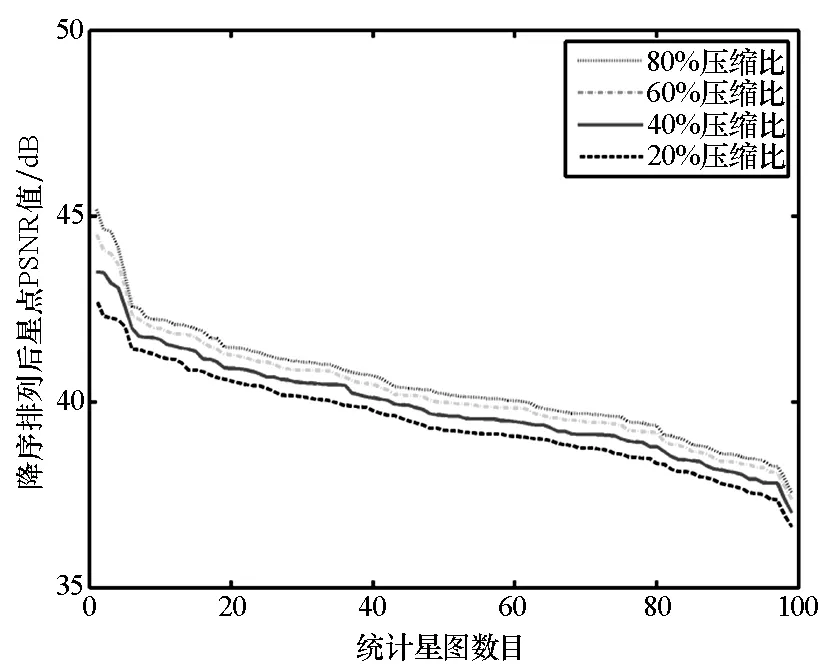
(b) GPSR算法稀疏重构图像PSNR(b) PSNR of sparse reconstruction by GPSR
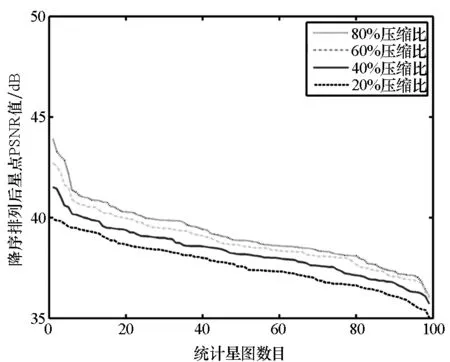
(c) OMP算法稀疏重构图像PSNR(c) PSNR of sparse reconstruction by OMP
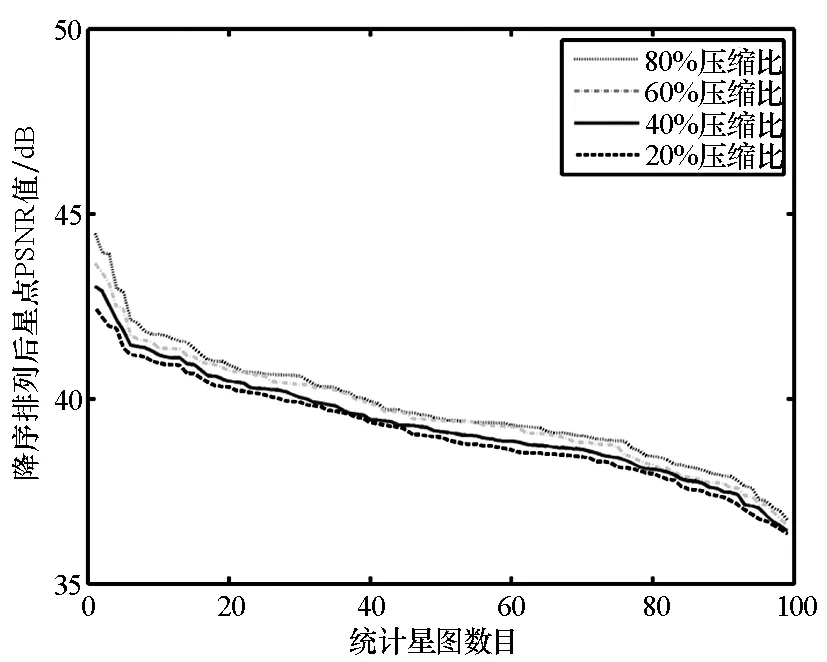
(d) CoSaMP算法稀疏重构图像PSNR(d) PSNR of sparse reconstruction by CoSaMP
表1对比了各重构方法在不同压缩比下对单幅星图的平均处理时间。结果表明,凸优化算法较贪婪算法所需重构时间更长,其中凸优化算法在各压缩比下的重构时间均大于12 s,而贪婪算法保持在1~4 s之间。理论上,由于两类算法在解决如式(5)和式(6)稀疏约束下的优化问题时求解过程不同,导致了二者在重构精度和运算时间上的差异。对比一般场景图像,星图在同等条件下所需重构时间更少,这是由于星图具有更高
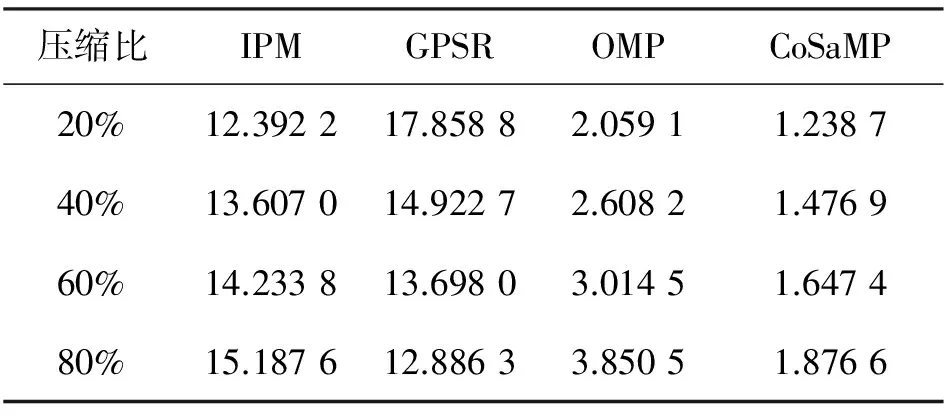
表1 运行时间对比Tab.1 Comparison of computation time s
的稀疏性,即待求解的系数向量α具有更少的非零元素,在整体上减少了求解时间。需要指出,IPM,OMP和CoSaMP三种算法的重构时间随着压缩比的增大而逐渐增加,而GPSR算法的重构时间随着压缩比的增大而减少,这是由于该算法的特点决定了较多的测量数能够有效加快收敛速度。

图3 原始星点Fig.3 Original star
3.2 单星点重构质量分析
通过一幅单星点图像考察稀疏重构对星点特征的影响。图3显示为一个16×16原始单星点图像,图4显示了利用选定的四种算法在压缩比为60%时的重构结果。相比原始星图,各算法重构星图中均出现了较为明显的噪声,并且重构星点的亮度也在不同程度上发生了改变,这是稀疏重构图像误差导致的必然结果。
在同等条件下对原始星点和重构星点进行提取,由质心法计算得到星点的质心位置,在图中用圆点表示。相比图3中原始星点质心位置,图4中各重构星点质心均发生了少量的偏移,在IPM,GPSR,OMP和CoSaMP四种算法下分别为0.12,0.15,0.21和0.20个像素单位。为了进一步考察重构星点的亮度变化,图5显示了各算法的图像重构误差,其中星点总像素区域Ωd内的较大误差区域(灰度差值≥10)如图中标示。可以看出,IPM和GPSR算法对星点的重构质量较高,表现为满足以上条件的误差区域较小,并且该区域内的误差值较低;相对地,OMP和CoSaMP算法对星点的重构质量稍低,表现为满足条件的误差区域和误差值均较大。四种算法对星点特征的重构质量从高到低依次为:IPM,GPSR,CoSaMP,OMP,该结果与3.1节在相同压缩比下对星图图像重构质量的顺序相一致。结果说明图像的重构质量直接关系到星点特征的重构情况,因此需要利用提出的指标对后者作进一步考察。

(a) IPM方法(a) IPM method (b) GPSR方法(b) GPSR method (c) OMP方法(c) OMP method (d) CoSaMP方法(d) CoSaMP method图4 四种算法稀疏重构星点Fig.4 Reconstructed star by four approaches

(a) IPM方法(a) IPM method (b) GPSR方法(b) GPSR method (c) OMP方法(c) OMP method (d) CoSaMP方法(d) CoSaMP method图5 四种算法图像重构误差Fig.5 Reconstruction error by four approaches
3.3 星点特征重构误差
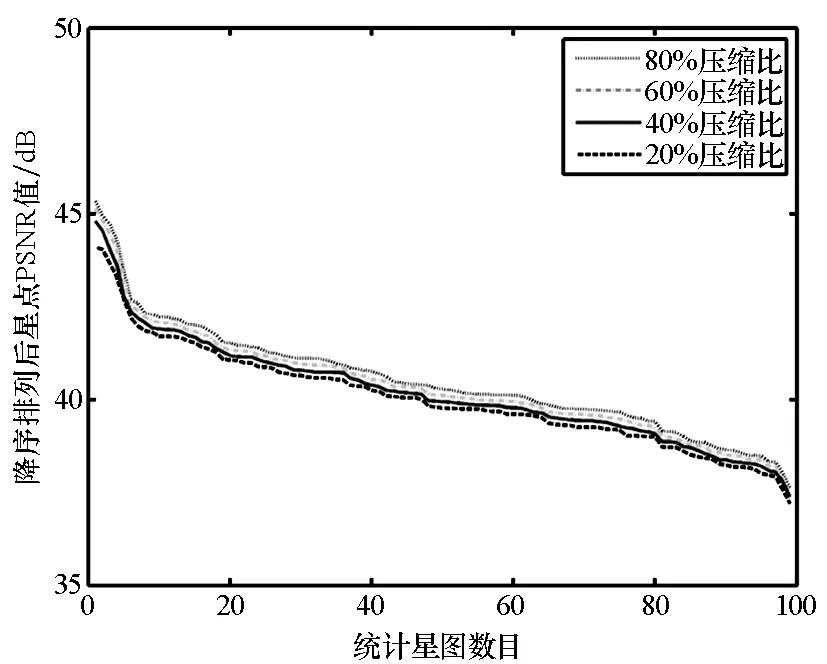
首先考察稀疏重构对星点亮度特征的影响。由单星点重构质量分析可知,星点的亮度误差主要表现为星点总像素区域Ωd内的灰度变化,通过star-PSNR指标对亮度误差进行评价。仿真中,按照3.1节的方法统计星库中星点的star-PSNR,并且为了与图像PSNR作对比分析,同样对背景误差background-PSNR进行统计。
图6显示了四种算法在不同压缩比下对star-PSNR的统计结果。数据显示,各算法普遍对星点区域实现了较高质量的重构,各压缩比下平均star-PSNR值均保持在45 dB以上。同时,四种算法对星点区域的重构精度从高到低依次为IPM,GPSR,CoSaMP和OMP,结果与图像重构误差一致。相比图2,在相同重构条件下,星点像素区域误差受压缩比变化影响较图像误差更加明显,其中压缩比每增加20%,star-PSNR值平均增大约5 dB。结果定量说明了提高压缩比能够相对有效地提升星点的重构质量,同时也证明了对星点区域重构误差进行单独考察的必要性。
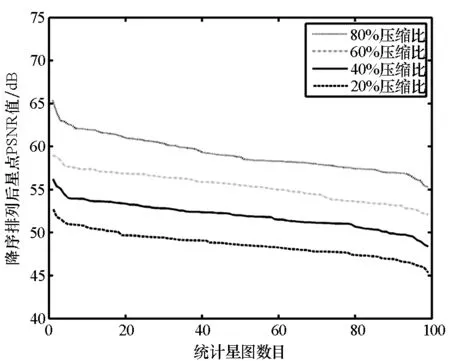
图7显示了同样方法下对图像库中各重构星图background-PSNR的统计结果。对比图2、图6和图7的统计结果,在相同重构算法下,图6的误差曲线与图2差异性较大,而图7的误差曲线与图2更为接近,这表明星图图像的重构误差在更大程度上取决于背景像素区域。分析图7与图2的区别,图7中背景区域的重构误差曲线在不同压缩缩比下表现得更为紧密,其中在IPM,GPSR和CoSaMP三种算法下各相邻压缩比间平均相差0.2 dB,在OMP算法下平均相差不到1 dB,这是由于星图背景内容较为单一,使得背景重构质量对压缩比的变化相比图像重构质量更加不敏感。
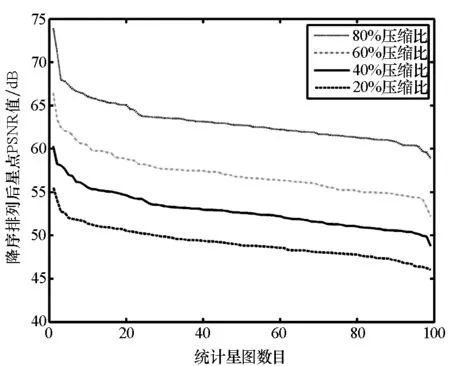
(a) IPM算法重构星点PSNR(a) Star-PSNR of sparse reconstruction by IPM
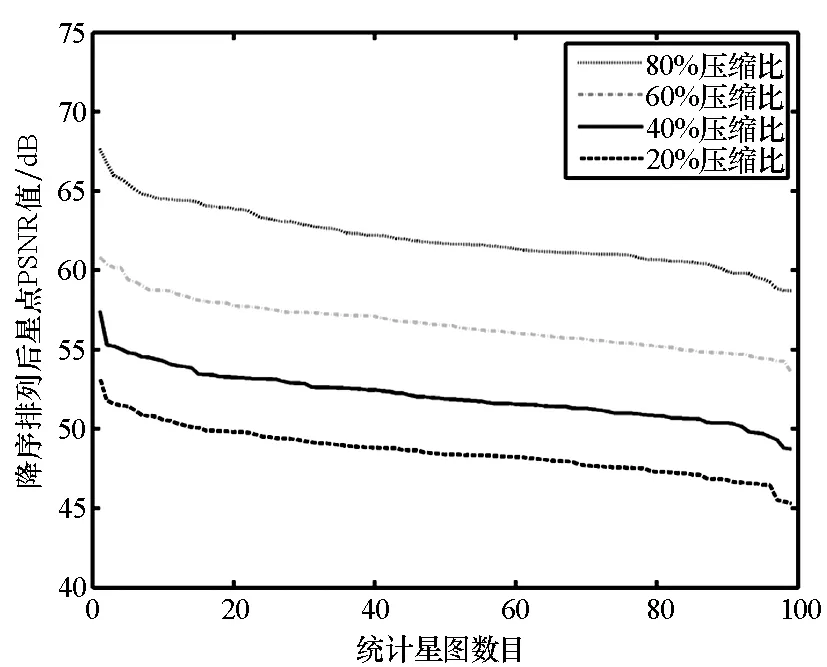
(b) GPSR算法重构星点PSNR(b) Star-PSNR of sparse reconstruction by GPSR
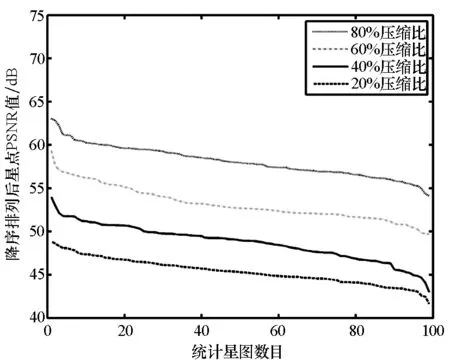
(c) OMP算法重构星点PSNR(c) Star-PSNR of sparse reconstruction by OMP
(d) CoSaMP算法重构星点PSNR(d) Star-PSNR of sparse reconstruction by CoSaMP
其次考察稀疏重构对星点质心位置的影响。根据单星点重构质量分析,星点区域的灰度变化会导致重构星点质心位置发生偏移。在同等条件下提取重构前后星点的质心位置,统计星图库中所有星点在不同重构算法、不同压缩比下的质心重构成功率,如表2所示。可以看到,星点质心重构成功率随着压缩比的增加而上升,与star-PSNR评价规律相一致。当压缩比取20%时,各算法对星点质心重构成功率大致保持在95%以上(除OMP算法为93.64%外),在一定程度上保证了在较低测量数目下利用重构星图进行姿态确定的成功率。
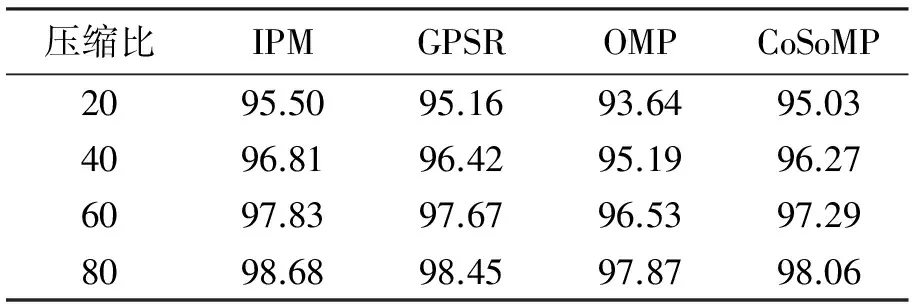
表2 星点质心重构成功率比较Tab.2 Comparison of the successful reconstruction rate of star centroid %
最后对稀疏重构造成的干扰星影响进行考察。由于在低压缩比下干扰星影响更为明显,为了便于对比统计,仿真中选定压缩比为20%。在图像库中,对于四种不同算法,分别统计缺失星和伪星在各重构星图中所占比例,并按降序进行排列,统计结果如图8所示。在IPM,GPSR,OMP和CoSaMP四种算法下,造成缺失星的星图数量分别是9,13,24和17幅,产生伪星的星图数量分别是13,18,29和25幅,重构过程中产生伪星的星图数量多于缺失星。对比四种算法下的结果,重构精度较高的算法产生干扰星的星图数更少,并且在相同星图中产生干扰星的数量更少。以ISM和OMP算法的缺失星情况为例,考察星图库中前四幅星图,前者产生缺失星的比例分别为1 ∶33,1 ∶36,0 ∶23和0 ∶26,而后者相应的比例为2 ∶33,1 ∶36,1 ∶23和1 ∶26。综合考虑,在产生干扰星的星图中,各算法在压缩比为20%时均能够保持干扰星占有率低于9%,进一步保证了在较低测量数目下姿态确定的成功率。
(a) IPM算法重构背景PSNR(a) Background-PSNR of sparse reconstruction by IPM
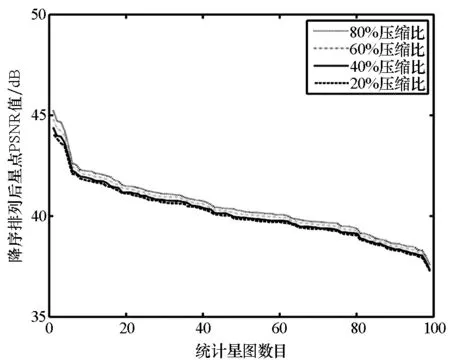
(b) GPSR算法重构背景PSNR(b) Background-PSNR of sparse reconstruction by GPSR

(c) OMP算法重构背景PSNR(c) Background-PSNR of sparse reconstruction by OMP
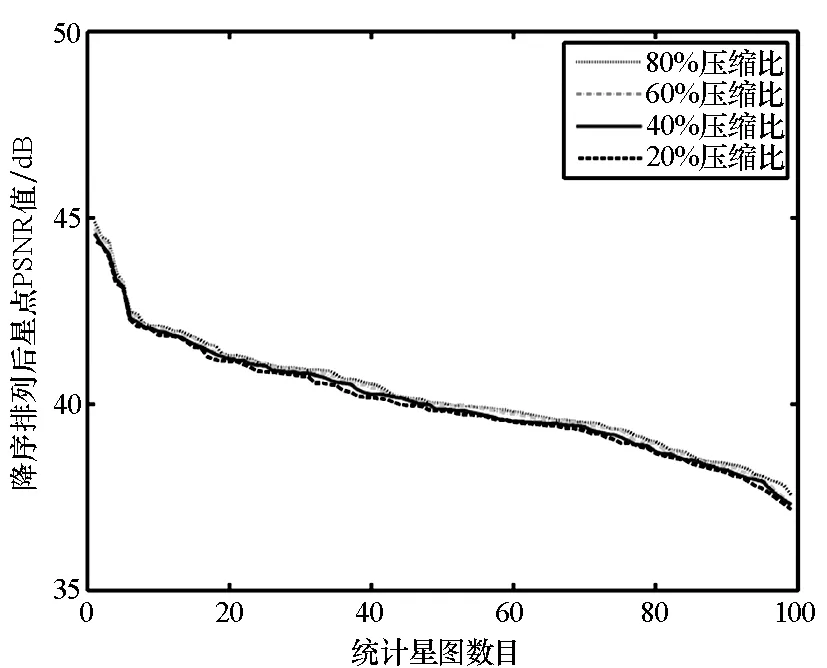
(d) CoSaMP算法重构背景PSNR(d) Background-PSNR of sparse reconstruction by CoSaMP
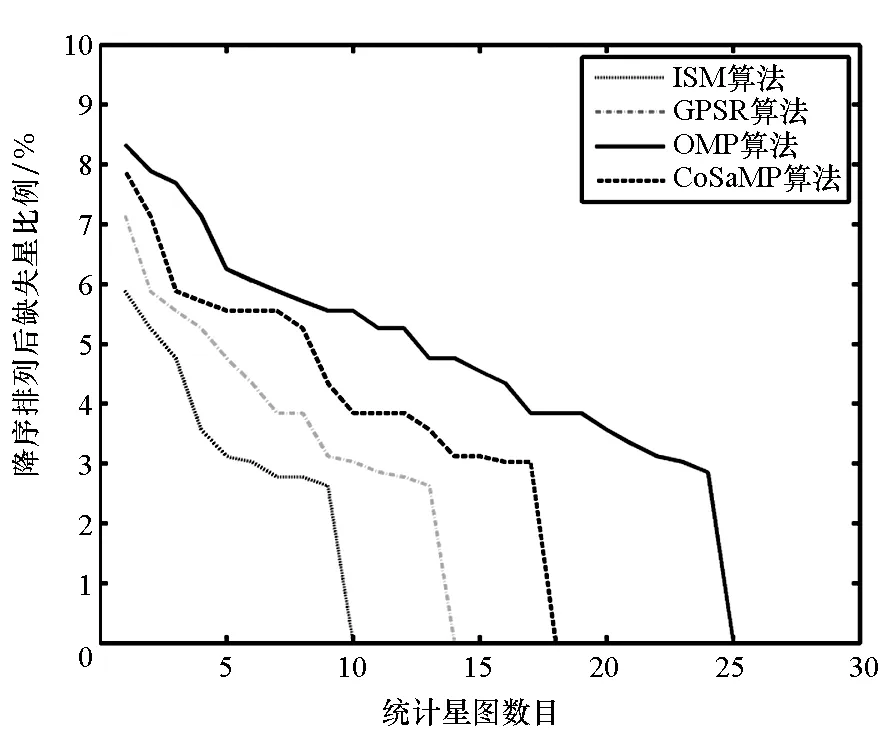
(a) 缺失星影响(a) Effect of missing stars
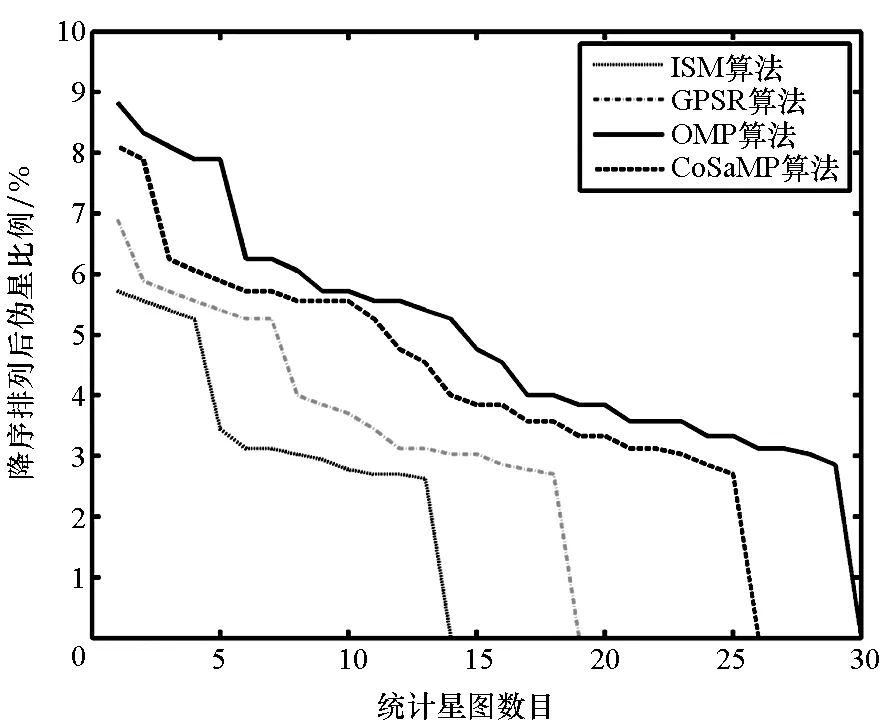
(b) 伪星影响(b) Effect of spurious stars
对于重构失败的星点,主要由于图像重构过程中灰度值的变化直接导致提取失败或者提取成功时质心偏移量过大,图9分别列举了本文涉及的几种重构失败的情况,星点均选自OMP算法压缩比为20%时的重构图像库。图9(a)显示了星点质心偏移超过1像素的情况,其中原始质心位置用圆点表示,重构后质心位置用星号表示;图9(b)显示了重构后星点提取失败情况,其中星点提取的背景灰度阈值选取为10,该星点在原始星图中能够成功提取,但重构后只有一个像素高于背景阈值,导致提取失败;图9(c)下方显示了一颗由于重构误差导致错误提取的干扰星,这是由于重构误差引起了较为集中的图像噪声,并构成了大于背景阈值的连通域,被提取算法误判断为“星点”。实际中,选用重构精度较高的算法或者提高压缩比都可以在一定程度上降低星点重构失败的概率。

(a) 质心偏移(a) Centroid excursion (b) 星点缺失(b) Missing star

(c) 干扰星(c) Spurious star图9 重构失败星点Fig.9 Failing reconstruction of star point
4 结论
本文从星图图像和星点特征两个方面定量分析了稀疏重构对星图的影响。结果表明,星图在四种不同重构算法、不同压缩比下均实现了较好的重构效果,图像平均PSNR保持在35 dB以上,同时表明星图在相等重构条件下较一般场景图像能够获得更高的重构质量以及更短的重构时间。对重构前后星点的质心误差、亮度误差和干扰星影响的分析表明,星点在四种不同算法各压缩比下平均star-PSNR值保持在45 dB以上,同时星点质心重构成功率基本保持在95%以上,且在较低测量数下能够保持干扰星占有率低于9%。该结果表明,星点在重构过程中能够在一定程度上保持可用于姿态确定的特征,进一步验证了压缩感知理论在星敏感器中应用的可行性,并为星敏感器压缩成像的实现提供现实依据。
References)
[1] Rogers D, Schwinger M, Kaidy J, et al. Autonomous star tracker performance[J]. Acta Astronautica, 2009, 65(1/2): 61-74.
[2] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[3] Candes E, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.
[4] 刘吉英. 压缩感知理论在成像中的应用[D]. 长沙:国防科学技术大学, 2010. LIU Jiying. Theory of compressive sensing and its application in imaging[D]. Changsha: National University of Defense Technology, 2010.(in Chinese)
[5] 严奉霞, 王泽龙, 朱炬波, 等. 压缩感知理论与光学压缩成像系统[J]. 国防科技大学学报, 2014, 36(2): 140-147. YAN Fengxia, WANG Zelong, ZHU Jubo, et al. Compressive sensing theory and optical compressive imaging systems[J]. Journal of National University of Defense Technology, 2014, 36(2): 140-147.(in Chinese)
[6] Ma J W, Khwaja A S, Hussaini M Y. Signal and image processing for remote sensing[M].USA:CRC Press, 2012: 73-90.
[7] 肖龙龙. 面向高分辨率遥感光学成像的压缩感知理论及方法研究[D]. 长沙:国防科学技术大学, 2012. XIAO Longlong. Research on theory and methods of compressed sensing for high resolution remote sensing optical imaging[D]. Changsha: National University of Defense Technology, 2012.(in Chinese)[8] 尹航, 宋新, 闫野. 星图的稀疏表示性能[J]. 光学精密工程, 2015, 23(2): 573-581. YIN Hang, SONG Xin, YAN Ye. Performance on sparse representation of star images[J]. Optics and Precision Engineering, 2015, 23(2): 573-581.(in Chinese)
[9] Song X, Yin H, Yan Y. Imaging method with low data rate for autonomous star trackers based on compressive sensing[J]. Journal of Electronic Imaging, 2015, 24(2): 023024-023024.
[10] 马坚伟, 徐杰, 鲍月全, 等. 压缩感知及其应用:从稀疏约束到低秩约束优化[J]. 信号处理, 2012, 28(5): 609-623. MA Jianwei, XU Jie, BAO Yuequan, et al. Compressive sensing and its application: from sparse to low-rank regularized optimization[J]. Signal Processing, 2012, 28(5): 609-623.(in Chinese)
[11] Candès E J, Wakin M B, Boyd S P.Enhancing sparsity by reweightedl1minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877-905.
[12] Tropp J A. Greed is good: algorithm results for sparse approximation[J]. IEEE Transaction on Information Theory, 2006, 50(10): 2231-2342.
[13] Kim S, Koh K, Lustig M, et al. An interior point method for large-scalel1regularized least squares[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 606-617.[14] Figueiredo M A T, Nowak R D, Wright S J.Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-598.
[15] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.
[16] Needell D, Tropp J A. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301-321.
[17] 张广军. 星图识别[M]. 北京:国防工业出版社, 2011. ZHANG Guangjun. Star identification[M].Beijing: National Defense Industry Press, 2011.(in Chinese)
[18] Shortis M R, Clarke T A, Short T. A comparison of some techniques for the subpixel location of discrete target images[J]. SPIE Videometrics Ⅲ, 1994, 2350: 239-250.
Effect of compressive sensing sparse reconstruction on star image
YIN Hang, YAN Ye, SONG Xin
(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)
The sparse reconstruction is one of the key factors in compressive sensing theory. In order to apply sparse reconstruction to compressive imaging process of star tracker in an effective way, the effect of sparse reconstruction on star image was analyzed from the perspectives of star image error and star feature error. For the problem of image error, PSNR(peak signal-to-noise ratio) evaluation index was employed to observe reconstruction quality of star image under different reconstruction algorithm and diverse compression ratio. For the problem of feature error, firstly, the influential mechanism of sparse reconstruction on star feature was analyzed theoretically; and then the evaluation index of reconstruction error of star feature was proposed to investigate the reconstruction error of star centroid, brightness and number. Result shows that, the star image can obtain higher reconstruction quality than the common image with the same reconstruction condition under diverse compression ratio of selected algorithm, and the reconstructed star can keep its features for attitude determination to a large extent. The conclusion proves the validity of attitude estimation by using the reconstructed star image, verifies the feasibility of applying compressive sensing to star tracker and provides the practical foundation for compressive imaging of star tracker.
compressive sensing; sparse reconstruction; star tracker; star image
10.11887/j.cn.201606016
2015-07-22
国家自然科学基金资助项目(61401487)
尹航(1985—),男,天津人,博士研究生,E-mail:yinhang@nudt.edu.cn; 闫野(通信作者),男,教授,博士,博士生导师,E-mail:yynudt@126.com
TP391.41
A
1001-2486(2016)06-095-09
http://journal.nudt.edu.cn
