桨叶安装角度对反应器内混合特性影响的模拟分析
2017-01-07尹伟齐曹秀芹赵振东
尹伟齐,曹秀芹,赵振东
(北京建筑大学 环境与能源工程学院 城市雨水系统与水环境省部共建教育部重点实验室,北京 100044)
桨叶安装角度对反应器内混合特性影响的模拟分析
尹伟齐,曹秀芹,赵振东
(北京建筑大学 环境与能源工程学院 城市雨水系统与水环境省部共建教育部重点实验室,北京 100044)
借助计算流体力学(Computational Fluid Dynamics, CFD)技术对桨叶安装角度为30°,45°和60°的污泥厌氧消化反应器进行数值模拟,研究结果表明:反应器内最大速度出现在搅拌桨叶末端,搅拌轴处及其两侧速度几乎为零,形成死区. 湍流黏度的最大值均出现在搅拌轴上部左右两侧的区域,搅拌桨叶区域的湍流黏度较小. 湍动能的最大值出现在桨叶末端附近,并向中心逐渐递减,且随着安装角度增大,湍动能的分布更加广泛和均匀,三种反应器的湍动能耗散主要集中在桨叶区和槽壁区域,安装角度越大,在桨叶区和槽壁区域的耗散就越大,不利于反应器内能量的传递. 桨叶安装角度越大,其搅拌功率越小,安装角度每增加5°,功率降低约1%.
厌氧消化; 桨叶安装角度; CFD模拟; 搅拌混合; 搅拌功率
厌氧消化处理是对剩余污泥进行稳定化、减量化和资源化的一种处理方法[1],得到了主张污泥回收再利用的欧美发达国家的关注,并成为污泥处理处置的主流技术之一[2]. 搅拌过程是污泥生物处理过程的重要环节[3],其主要作用是提供所需的机械能以及合适的流动形式,以达到促进污泥与菌种混合均匀、促进传质传热的均匀性和防止污泥的结团等. 流体是反应器中物质和能量传递的主要载体,仅依靠经验公式设计出的反应器无法对其水力特性进行精确的预测,从而制约着反应器的处理效果[4]. 污泥作为一种不透明的非牛顿流体,通常情况下无法全面地获得厌氧消化反应器中的流动类型及流动特性. 计算流体力学(Computational Fluid Dynamics, CFD)技术已证明在流体力学特征上是一种非常有力的工具[5].
曹乔乔等[6]利用Ansys CFX软件对自吸式龙卷流型搅拌槽内的气、液、固三相混合特性进行了研究,并与标准搅拌槽进行对比,得出自吸式龙卷流型搅拌槽有利于物料之间的充分接触与混合,节能效果明显. 罗宇笛等[7]采用Fluent对50L全自动发酵罐内不同桨叶组合的搅拌效果进行气液两相模拟,以此优化出一种搅拌效果较好的桨型组合,并与原始组合比较,混合效果提高1.1倍. 武光霞[8]对不同桨叶涡轮式搅拌器进行数值模拟,并对直斜叶交替组合搅拌器和上直叶下斜叶组合搅拌器进行对比分析,发现直斜叶交替组合搅拌器在两桨之间区域的搅拌得到加强,混合较好,整体搅拌效果有所改善. Uluaga等[9]用CFD技术模拟了厌氧膜生物反应器,结果表明,该厌氧膜生物反应器具有较好的混合效果和该厌氧生物膜呈现出较高的剪切应力. Azargoshasb等[10]结合厌氧发酵产酸的平衡方程,对连续搅拌反应器内的产甲烷反应进行了气、液、固的CFD模拟,仿真模拟结果表明,反应器的挥发性脂肪酸的降解效率和模型与实验结果吻合得很好,尤其在低浓度进水挥发性有机酸时,模拟结果和实验结果吻合得更好. ZMurthy等[11]运用CFD技术模拟了气- 液- 固三相流,研究不同桨径、转速、含固率等条件的固体悬浮的临界转速,通过与实验对比,表明CFD技术能够对流体力学特性进行准确地描述. 项目组前期已经借助CFD技术对消化反应器混合效果及能耗进行模拟分析,并通过了实验验证确定180 r/min的转速为反应器搅拌混合均匀的最佳转速,且采用CFD技术对桨叶类型及结构特征进行了优化研究[12].
因此,在项目组前期模拟和实验研究的基础上,采用Ansys 15.0软件对不同安装角度的搅拌桨叶的厌氧消化反应器进行模拟,重点结合速度场等方面对反应器的数值模拟结果进行分析.
1 计算模型
1.1 控制方程
1.1.1 质量守恒方程
质量守恒方程也叫连续性方程,任何流动问题都应该满足质量守恒定律,按照质量守恒定律,单位时间内流出控制体的流体净质量之和应等于相同时间间隔控制体内因密度变化而减少的质量,所以质量守恒方程的微分形式为:
(1)
式中:μx,μy,μz分别表示X,Y,Z轴三个方向的速度分量;t为时间;ρ为流体密度.
1.1.2 动量守恒方程
动量方程的本质满足牛顿第二定律:对于一给定的流体微元,其动量对时间的变化率等于外界作用在该微元体上的各种力之和,因此动量守恒方程的微分形式为:
(2)
式中:μi,μj分别表示流体沿i,j方向的速度;xi,xj为流体沿i,j方向的位移;t为时间;ρ为流体密度;p为流体微元体上的压强;fi为i方向的单位质量力.
1.2 湍流模型
用最基本的两参数标准κ-ε模型处理湍流效应,湍动能κ和湍动能耗散率ε的通用方程表达式为:
(3)
式中:ρm表示混合物的密度;vm表示相平均速度;Sφ表示相应的源项,湍流黏度μtm的表达式为:
μtm=cμρmk2/ε
(4)
1.3 几何模型
图1是实验装置厌氧消化反应器的示意图,反应器罐口直径D1为230mm,反应器直径D2为340mm,反应器的高度H1为440mm,液位高度300mm,桨叶安装高度(距反应器底部)100mm,桨叶长度90mm,桨叶宽度80mm.
图1中,1—恒温水浴加热装置;2—出料口及阀门;3—搅拌桨叶;4—搅拌杆;5—反应器罐体;6—电动机座垫;7—电动机;8—进料口及阀门;9—气体收集装置;10—恒温水浴加热装置内的支撑杆.
图2表示搅拌桨叶安装角度为30°,45°和60°的反应器几何模型示意图,定义桨叶安装角度α如图2(d)中所示.
1.4 模拟物系
污泥在厌氧消化反应器内混合及发酵过程中,产生的气体相对于污泥混合液的量较少,对污泥流体的扰动相对于搅拌设备的混合作用很小,因此在本研究的CFD模拟过程中予以简化. 该样品取自北京某污水处理厂的剩余污泥,污泥混合液的密度为1 050kg/m3,pH为6.75,有机物含量为2 780mg/L,氨氮为195.90mg/L,总固体含量为4.12g/L. 初始状态污泥会有一部分沉淀在反应器底部,当桨叶转动后会悬浮起来充满整个反应器.
2 CFD模拟
2.1 模拟方法
湍流模型采用标准的κ-ε模型. 计算域的旋转运动部分采用多重参考系法(MultiReferenceFrame,MRF)[13-15]进行处理,通过交界面进行质量、动量和能量的传递,用Scalable壁面函数对边界层进行处理. 采用SIMPLE算法的半隐式方法求解控制方程,计算时采用固定时间步长0.001s,连续性、速度场和湍流场残差小于0.000 1,直至结果达到预期的收敛效果[16].
2.2 网格划分
采用非结构四面体网格对反应器内的计算域进行划分,并采用Inflation对安装角度分别为30°,45°和60°的搅拌桨叶进行网格局部细化,网格划分结果如图3所示. 桨叶安装角度为30°,45°和60°时,反应器的网格划分总节点数为195 964,195 687和195 525个,网格数量为213 845,213 509和213 141个,并采用OrthogondQuality对网格质量进行检查,MeshMetric的最小值为0.19,0.16和0.17,均大于0.05且网格没有出现负体积,因此网格可以接受.
2.3 边界条件
将计算域分为动、静两个区域,对搅拌桨叶、搅拌轴、定子区和转子区分别设置. 内部动区域包括旋转的搅拌桨叶,将动区域内的流体设为与搅拌桨相同的转速进行旋转,外部静区域包括反应器壁,静区域内的流体看作是静止的. 将搅拌轴和桨定义为动边界,将反应器壁面定义为静止壁面边界条件.
3 模拟结果与分析
3.1 速度场分析
桨叶安装角度为30°,45°和60°的厌氧反应器纵剖速度矢量图如图4所示. 模拟结果表明,桨叶排出的污泥流体在遇到反应器壁后有向上和向下流动的现象,桨叶区域内有漩涡出现,反应器内污泥流体的运动既存在径向流也存在轴向流. 三种安装角度的反应器内最大速度均出现在搅拌桨叶末端,最大速度约为0.13m/s, 0.14m/s和0.15m/s,接近轴处的速度几乎为零. 在消化反应器底部和上部,污泥流体的速度偏低,这是因为在这些区域受到搅拌桨叶的推动力较小,污泥甚至在反应器上部轴的两侧几乎没有运动,形成死区,直接影响反应器内污泥流体的混合效果,因此有必要对消化反应器桨叶进行优化,提高搅拌混合性能,提升厌氧消化反应效果.
3.2 湍流黏度
图5表示搅拌桨叶安装角度为30°,45°和60°时的湍流黏度. 研究结果发现,湍流黏度的最大值均出现在搅拌轴上部左右两侧的区域,搅拌桨叶区域的湍流黏度较小,这是因为,污泥作为一种非牛顿流体,在搅拌桨叶区域,湍动能相对比较大,有利于污泥在桨叶区域混合均匀,而在搅拌轴上部左右两侧,湍流黏度达到最大值,污泥在此区域形成了死区,搅拌混合效果不理想.
3.3 湍动能
30°,45°和60°三种桨叶安装角度的反应器在高25mm截面处的湍动能如图6所示. 结果表明,三种不同安装角度的反应器,其湍动能均是分布在桨叶区域内,且随着安装角度的增大,湍动能分布愈加广泛并均匀,这有利于底部污泥的悬浮,为污泥流体的径向运动提供能量,促进污泥在消化反应器内部混合均匀. 由于强烈的向心流,湍动能的最大值出现在桨叶末端附近,并向中心逐渐递减,湍动能的最小值出现在桨叶区域底部和上部,该区域为死区.
3.4 湍动能耗散
湍动能耗散影响物料分布和混合状况,对传质影响很大,因此对反应器来说湍动能耗散非常重要[17]. 三种安装角度的反应器在高25mm截面处的湍动能耗散如图7所示. 模拟结果表明,三种反应器的湍动能耗散主要集中在桨叶区和槽壁区域,部分湍动能耗散为分子内能,这是由于污泥流体与桨叶、槽壁的撞击过程中会产生速度突变,并在附近出现漩涡现象,加剧能量的消耗,安装角度越大,在桨叶区和槽壁区域的耗散就越大,不利于反应器内能量的传递,因此有必要在反应器能量耗散方面进一步改进,提高反应器内部能量的传递效率.
3.5 功率计算
搅拌功率准数表示机械搅拌所施加于单位体积被搅拌液体的外力与单位体积被搅拌液体的惯性力之比,可反应功率消耗的情况,其表达式为:
NP=P/ρN3D5
(5)
式中:NP为搅拌功率准数;P为搅拌功率,W;ρ为液体密度,kg/m3;N为搅拌转速,r/min;D为搅拌桨叶直径,m.
其中,搅拌功率P=2πMN. 采用Fluent15.0中的ForceReports,选择Moments,计算得出三种不同安装角度桨叶反应器的扭矩如表1所示,从而计算得到三种不同安装角度搅拌器的功率准数. 由表1得出,安装角度越大,搅拌过程中所消耗的功率越小,有利于降低功率.
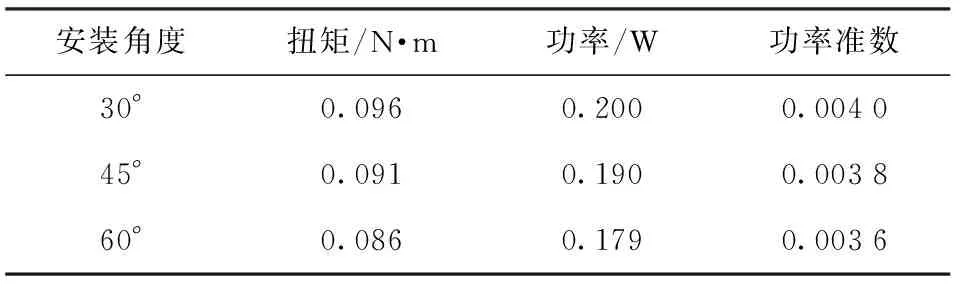
表1 不同桨叶安装角度反应器的功耗参数
3.6 功率与桨叶安装角度的关系
计算不同搅拌桨叶安装角度的反应器功率,并对其进行拟合,可以有效预测不同安装角度下反应器的功率消耗,及时对安装角度进行调整. 拟合结果如图8所示,拟合度R2为0.992 8,拟合方程为:
W=-0.000 65·α+0.218 5
(6)
式中:W为搅拌功率;α为安装角.
由功率和安装角度的关系可以得出,随着安装角度的增大,搅拌过程中的能量消耗是逐渐减小的,安装角度每增加5°,功率消耗降低约1%,有利于功耗的节约. 搅拌桨安装角度的选择,并不是越小越好,还应结合实际工程的物料截面有效扰动半径、能耗、搅拌混合效果等方面综合考虑.
4 结论
1) 污泥流体在反应器内有轴向流和纵向流,反应器内最大速度出现在桨叶末端,接近轴处的速度几乎为零,形成死区. 反应器内湍流粘度的最大值出现在搅拌轴上部左右两侧的区域,这是死区形成区域,搅拌混合效果不理想,搅拌桨叶区域的湍流粘度较小,有较好的搅拌混合效果.
2) 湍动能随着桨叶安装角度的增大,分布愈加广泛并均匀,有利于底部污泥的悬浮,为污泥的径向运动提供能量,促进污泥在反应器内部混合均匀. 湍动能的最大值出现在桨叶末端附近,并向中心逐渐递减. 湍动能耗散主要集中在桨叶区和槽壁区域,安装角度越大,在桨叶区和槽壁区域的耗散就越大,不利于反应器内能量的传递.
3) 桨叶安装角度越大,搅拌功率越小,拟合得出搅拌功率和安装角度的函数关系,有利于功率的准确预测,为消化反应器安装角度的调整提供依据,但安装角度的选择,还应结合实际工程中的物料截面有效扰动半径、能耗、搅拌混合效果等方面综合考虑.
[1] Yan Y Y, Chen H L, Xu W Y, et al. Enhancement of biochemical methane potential from excess sludge with low organic content by mild thermal pretreatment[J]. Biochemical Engineering Journal, 2013,70(2):127-134
[2] Kelessidis A, Stasinakis A S. Comparative study of the methods used for treatment and final disposal of sewage sludge in European countries[J]. Waste Management, 2012, 32(6): 1186-1195
[3] 韩丹,李龙,程云山,等.叶轮式搅拌器的研究进展[J].合成橡胶工业, 2005, 28(1):71-74
[4] 冯骞,薛朝霞,汪翙. 计算流体力学在水处理反应器优化设计运行中的应用[J]. 水资源保护, 2006, 22(2):11-15
[5] 范茏,施汉昌,徐农,等.污水处理反应器的计算流体力学[M]. 北京:中国建筑工业出版社,2012:1-10
[6] 曹乔乔,郝惠娣,王瑾,等.搅拌槽内三相混合特性的数值模拟[J].化工机械, 2015 (4): 548-553
[7] 罗宇笛,李啸,石小丹.采用计算流体力学仿真优化50L发酵罐搅拌系统[J].天津农业科学, 2015, 21(5): 46-50
[8] 武光霞.涡轮式组合搅拌器流场模拟研究[D]. 山东青岛:青岛科技大学,2014
[9] Zuluaga L C, Naranjo L N, Svojitka J, et al. CFD Simulation of an Anaerobic Membrane BioReactor (AnMBR) to Treat Industrial Wastewater[J]. Rev Ing, 2015,42: 23-29
[10] Azargoshasb H, Mousavi S M, Amani T, et al. Three-phase CFD simulation coupled with population balance equations of anaerobic syntrophic acidogenesis and methanogenesis reactions in a continuous stirred bioreactor[J]. Journal of Industrial & Engineering Chemistry, 2015, 27:207-217
[11] Murthy B, Ghadge R, Joshi J. CFD simulations of gas-liquid-solid stirred reactor: Prediction of critical impeller speed for solid suspension [J]. Chemical Engineering Science, 2007, 62(24): 7184-7195
[12] 曹秀芹,杜金海,李彩斌,等.污泥厌氧消化搅拌条件的优化分析[J].环境科学与技术,2015,38(1):100-105
[13] Alves S, Miaia C, Vasconcelos J, Experimental and modeling study of gas dispersion in a double turbine stirred tank[J]. Chemical Engineering Science,2002,57(3):487-496
[14] Jahoda M, Mostk M, Kukukova A, CFD modeling of liquid homogenization in stirred tanks with one and two impellers using large eddy simulation[J]. Chemical Engineering Research and Design, 2007,85(5):616-625
[15] Kasat G, Khopkar A, Ranade V, CFD simulation of liquid-phase mixing in solid-liquid stirred reactor[J]. Chemical Engineering Science, 2008,63(15):3877-3885
[16] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社, 2004:13-16
[17] Baldi S, Yianneskis M. On the quantification of energy dissipation in the Impeller stream of a stirred vessel from fluctuating velocity gradient measurements [J]. Chemical Engineering Science, 2004, 59(13):2659-2671
[责任编辑:王志兵]
Simulation Analysis of the Influence of Blade Installation Angles on Mixing Characteristic in the Reactor
Yin Weiqi, Cao Xiuqin, Zhao Zhendong
(School of Environment and Energy Engineering, Key Laboratory of Urban Rainwater System and Water Environment, Ministry of Education, Beijing University of Civil Engineering and Architecture, Beijing 100044)
With the help of CFD technology, sludge anaerobic digestion reactor is separately simulated with the blade installation angle of 30°, 45° and 60°. Results show that the maximum speed of the reactor appears at the end of the stirring blade, and it is almost zero at the shaft and its two sides, where the dead zone arises. The maximum value of the turbulent viscosity appears in the area of the upper left and right sides of the shaft, and the turbulent viscosity of the blade region is small. The maximum value of turbulent kinetic energy lies in the end of the blade, which gradually decreases toward the center, and the distribution of turbulent kinetic energy becomes extensive and uniform along with the increase of installation angle. For the three reactors, turbulent kinetic energy dissipation mainly concentrates in the area of blade and groove wall, and the dissipation becomes greater along with the installation angle increasing in these areas, which is not conducive to energy transmission in the reactor. The stirring power becomes smaller along with the increase of installation angle of blade, and the power reduces by about 1% for each increase of 5°.
anaerobic digestion; blade installation angle; CFD simulation; mixing; stirring power
2016-07-31
北京市自然科学基金重点项目(KZ201310016017)
尹伟齐(1991—),男,硕士研究生,研究方向:市政工程.
1004-6011(2016)04-0033-06
X703.1
A
