对课题学习最短路径问题的探究

新疆乌鲁木齐市第四十二中学 侯学琴

对课题学习最短路径问题的探究

新疆乌鲁木齐市第四十二中学 侯学琴

最短路径问题在现实生活中经常遇到，初中阶段，主要以“两点之间，线段最短”“连接直线外一点与直线上各点的所有线段中，垂线段最短”为知识基础，有时还要借助轴对称、平移、旋转等变换进行研究。

本节课以数学史中的一个经典问题——“将军饮马问题”为载体，开展对“最短路径问题”的课题研究，让学生经历将实际问题抽象为数学的线段和最小问题，再利用轴对称将线段和最小问题转化为“两点之间，线段最短”问题。

在安排这节课时始终把握一点：如何把问题转化成学生熟悉的“两点之间，线段最短”。

“学生是学习的主体”，在如何让学生成为学习的主体这个问题上，我采用了导学案的形式来引导学生自主探究学习。从学生熟悉的知识入手，给出如下例题：

1.如图所示，从A地到B地有三条路可供选择，你会选走哪条路？你的理由是什么？

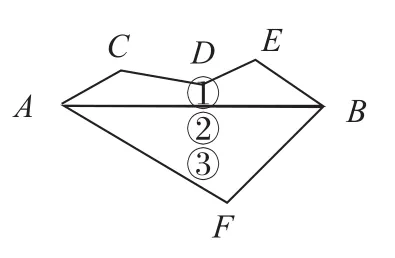
学生根据已有的知识经验“两点之间，线段最短”，很容易解决问题。给学生定好起点，先研究从两点在一条直线异侧，到异侧两点距离和最短开始，给出第二道例题：

2.如图，要在燃气管道L上修建一个泵站，分别向A、B两村供气，泵站修在管道的什么地方，可使所用的输气管线最短？

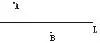
思考：为什么这样做就能得到最短距离呢？你如何验证PA+PB最短呢？

讲清楚这道题后，后续的两个探究都通过一些方法把问题转化成两点在一条直线的异侧，找最短路径，知识点不变，只是方法不同而已，让两点在一条直线的异侧，找最短路径贯穿始终成为本节课的主线，我们只是利用了轴对称和平移这两种方法来辅助我们完成知识点的学习。

在研究从两点在一条直线同侧，到同侧两点距离和最短，从学生感兴趣的故事引入，介绍“将军饮马问题”：古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦。有一天，一位将军专程拜访海伦，求教一个百思不得其解的问题，精通数学、物理学的海伦稍加思索，利用轴对称的知识回答了这个问题.这个问题后来被称为“将军饮马问题”。给出探究一。

【问题探究一】如图，牧马人从马棚A牵马到河边l饮水，然后再到帐蓬B。问：在河边的什么地方饮水，可使所走的路径最短？ 和学生一起分析，把实际问题转化成数学问题。

思考：能把A、B两点从直线l的同侧转化为异侧吗？

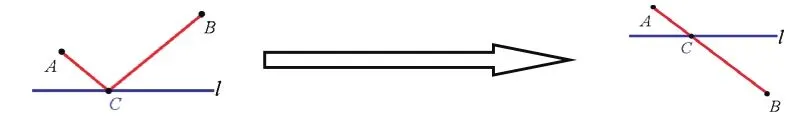
这个问题的提出，学生很容易想到我们刚学完的轴对称，利用轴对称变换转化成上面完成的两点在一条直线异侧，利用“两点之间，线段最短”找到最短路径。

然后继续给出思考：为什么这样做就能得到最短距离呢？你如何验证PA+PB最短呢？

检验学生的预习结果，在黑板上讲解如何利用三角形两边之和大于第三边来证明这一结果，强调清楚任意取一点中的“任意”二字，让学生理解任意的含义。再给出两个变式：

【变式一】如图，牧马人要把马从马棚A牵到草地边吃草，然后到河边饮水，最后再回到马棚A。

【变式二】如图，某一天牧马人要从马棚A牵出马到草地边吃草，再到河边饮水，最后回到帐篷B，请你帮他确定这一天的最短路线。

在课堂教学中，教师若能恰到好处地进行“一题多变”，不仅可以扩充知识容量，而且有利于促进学生数学思维能力的培养。学生有差异，教师要及时总结知识和方法，给学生形成一定的经验，等一等思维慢的孩子，弥补这部分孩子的思维漏洞，给出如下知识总结，帮他们梳理知识：

【归纳小结】1.学了三种情况下的最短路径问题

（1）两点在一条直线同侧；（2）一点在两相交直线内部；（3）两点在两相交直线内部。

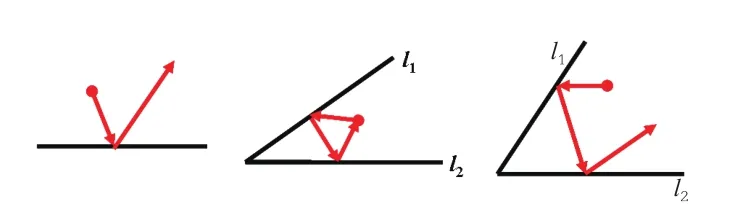
2.关键

作对称点，利用轴对称的性质将线段转化，从而利用“两点之间，线段最短”来解决问题。

在解决探究两地问题上利用了折纸，通过折叠使河的两岸重合在一条直线上，再次把问题转化成我们熟悉的两点在一条直线的异侧，利用“两点之间，线段最短”找到最短路径，上一个探究我们利用了轴对称的方法进行转化，在这个探究中，学生在折纸的过程中就会自然地联想到利用平移的方法进行转化，为平移桥或点做好铺垫，为后续的讲解提供了思路和方法，使得知识的生成自然流畅，易于理解，较好地解决了本节的难点。

【问题探究二】造桥选址问题中的最短路径问题

如图，A和B两地在一条河的两岸，要在河上造一座桥MN，桥造在何处可使从A到B的路径AMNB最短？（假定河的两岸是平行的直线，桥要与河垂直）

【归纳总结】 在解决最短路径问题时，我们通常利用______等变化把已知问题转化为容易解决的问题，从而作出最短路径的选择。

给出一组拓展题巩固所学知识，对学生的思维提升和训练。

【拓展题——勇攀高峰】

（1）在AB上找一点P，使得PM+PN最小；

（2）在OB上找一点P，使得DP+AP最小；

（3）在MN上找一点P，使得AP+BP最小；

（4）在对称轴上找一点P，使得CP+AP最小。

学生利用本节课的知识解决问题。这些图形都是轴对称图形，给学生充分的讨论时间，4人小组合作解决问题并相互讲解，派代表到黑板上解决问题，学生讨论的同时，教师在黑板上画出图形，学生解决完，教师作为对孩子出色表现和积极参与的奖励，给孩子讲故事，故事的内容是：数学家高斯18岁时，晚上照例做导师每天多给他布置的几道难题。有一道题写在小纸条上，几个小时过去了，他还是找不到解答方法。但越是困难，他越想攻克，一直持续到天亮，终于解开了这道题。第二天，导师接过他的作业一看，惊呆了，激动地说：“你知道吗？这是一个有两千多年历史的数学悬案！阿基米德没有解出，牛顿没有解出，我也正在研究它，昨天不小心把它夹在给你的作业里，你竟然……”很多年后，高斯回忆起这件事时，说：“如果导师告诉我那是一道两千年没有解开的难题，我不可能在一个晚上就把它解答出来。”孩子们，你们也正在经历和高斯相似的这一伟大过程，你们知道吗，你们刚解决的这四个问题是我们中考压轴题的一部分，它们的原型是（屏幕上呈现出来）：

【变式一】背景为等腰三角形

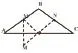
如图,已知在等腰三角形△ABC中,P是底边AC上的一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2，求△ABC的周长。

【变式二】背景为长方形、正方形

如图所示，四边形OABC为正方形，边长为3，点A，C分别在x轴，y轴的正半轴上，点D在OA上，且D的坐标为（1，0），P是OB上的一动点，则“求PD+PA和的最小值”要用到的数理依据是（ ）

A.“两点之间，线段最短”

B.“轴对称的性质”

C.“两点之间，线段最短”以及“轴对称的性质”

D.以上答案都不正确

在教学中教师应该注意用好课本，读懂、理解、吃透教材，全面掌握基础知识，领悟和把握真正的知识体系和能力结构。

结合重点内容与概念是“双基”教学的核心内容，是升学考试的必考内容，并且占的比重比较大，因此选择例题要针对重点内容与概念巩固“双基”训练，提高解题能力。

选择例题分步设问，要由浅入深，由易到难，使学生掌握新知识，提高解题能力。

注重数形结合，数形结合是研究数学问题常用的一种方法，是学生正确理解、深刻体会知识的好方法。

开阔思路，一题多解。一题多解可以培养学生解题的思考能力，更可以通过较少的题目复习较多的基础知识，并激发学生的求知欲。

注意题目的变式和引申，抓住例题的特殊点，多角度，全方位探索，培养学生的思维能力。