图形的魅力——论“几何直观”在小学低段数学中表现的几种形式

浙江省诸暨市海亮小学 陈 慧

图形的魅力
——论“几何直观”在小学低段数学中表现的几种形式

浙江省诸暨市海亮小学 陈 慧

《义务教育数学课程标准（2011年版）》（以下简称《标准》）先后多处就“几何直观”的教学提出了明确要求。本文仅结合小学数学课堂教学的典型案例，谈谈“几何直观”在小学低段数学中表现的几种形式。

几何直观；低段数学；表现形式

“几何直观”的内涵可以从两个角度进行解析：一是几何，在这里几何是指图形；二是直观，这里的直观不仅仅是指直接看到的东西，更重要的是依托现在看到的东西和以前看到的东西进行思考、想象。

作为新课程标准在“课程内容”中重点阐述的应该发展学生“10大核心概念”之一，对于几何直观，《标准》还明确指出：几何直观主要是指利用图形描述和分析问题，借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。此外，对于数学直观，著名数学家徐利治先生也有过对几何直观的描述：几何直观是借助于见到的或想到的几何图形的形象关系，产生对数量关系的直接感知。西方哲学家通常认为，直观就是未经充分逻辑推理而对事物本质的一种直接洞察，直接把握对象的全貌和对本质的认识。以这些理论知识作为基础，结合个人的思考和分析之后认为：几何直观就是依托、利用展现或想象出来的几何图形进行数学地思考和想象，它在本质上是一种通过图形所展开的想象能力。

多年的小学低段数学课堂教学实践经历，使笔者充分意识到了培养和发展小学生“几何直观”能力的必要性和重要性。因而，对于依据知识自身的特点和儿童认知发展规律，实施有针对性的课堂教学，在以下几个方面结合具体的实例进行了思考和探索。

一、实物直观

即实物层面的几何直观，是指借助与研究对象有着一定关联的实际存在物，借助其与研究对象之间的关联，进行简捷、形象的思考，获得逻辑的、形式的结论。

案例一：为什么余数一定要比除数小

1.观察算式，得出结论

在二年级下册第六单元讲有余数的除法时，我让学生观察每个除法算式：

11÷5=2……1

12÷5=2……2

13÷5=2……3

14÷5=2……4

15÷5=3

16÷5=3……1

师：看看每个算式中的余数和除数，你们有什么发现？（学生没有头绪）

师追问：我把除数和余数标上不用的颜色，你们再仔细观察，余数和除数比，有什么关系？（余数都比除数小）

师：可是为什么余数都比除数小，余数能和除数一样大吗？

部分学生说出了如果余数和除数一样大，就可以再多商一个1，但还有一些同学似懂非懂、不明算理。

2.实物摆弄，探究规律

看到学生似懂非懂的表情，我知道虽然结论已经得出，但是学生还没有完全理解余数一定要比除数小的深层算理，为了挖掘出“余数一定要比除数小的”深层算理，我设置了问题情境，采用小组合作、动手操作的形式完成下面的问题。先让学生在小组内分一分，再全班反馈。

一组：有11个草莓，每5个为一份，可以分成几份？

二组：有12个草莓，每5个为一份，可以分成几份？

三组：有13个草莓，每5个为一份，可以分成几份？

四组：有14个草莓，每5个为一份，可以分成几份？

五组：有15个草莓，每5个为一份，可以分成几份？

六组：有16个草莓，每5个为一份，可以分成几份？

各组完成操作后，每个组派一名代表上台讲解自己组分的过程，有的小组借助笑脸，有的小组借助小棒，有的小组直接在黑板上画圆分析，有的小组用实物图分草莓，都说出了自己分的过程。

一组：11张笑脸，每5个为一份，可以分成两份， 还剩下1个，不够分了。

二组： 12根小棒，每5个为一份，可以分成两份，还剩下2根，不够分了。

三组：画了13个圆，每5个为一份，可以分成两份，还剩下3个，不够分了。

四组：画个14个草莓，每5个为一份，可以分成两份，还剩下4个，不够分了

……

待学生讲述完分法后，我让学生进一步观察，并提问：

师：剩下的为什么不分了？剩下多少的时候就不够分了？（1个、2个、3个、4个）

师：剩下5个够分吗？6个呢？

生1：剩下5个刚好分出1份，剩下6个，也能多分出1份呢！

生2：剩下的5个，或者比5个多，就能多分出1份。

师：现在你知道，余下的数和除数之间到底有什么关系了吧？（余数比除数小）

师：谁能再说说是为什么？

生1：如果余数比除数大了，那就还要再分一份，还要接着分。

生2：我觉得，余数和除数一样大了也不行，这样正好还能再分一份，刚好分完，就没有余数了。

师引导小结：余数一定要比除数小。

学生通过借助各种实物模型，直观形象地感受着余数与除数之间的关系，使得“余数一定要比除数小”不再只是学生机械地记在心里的一句法则，而是通过“数形结合”理解内化的数学知识。由此可见，实物直观，能较好地激发学生的学习兴趣、帮助学生理解，并为知识的后续学习奠定能力基础。

二、图形直观

图形直观是以明确的几何图形为载体，通过演绎、转化、推导、验证，从而得出结论的一种几何直观。

案例二：“求一个数是另一个数的几倍”

在“求一个数是另一个数的几倍”中，用到的线段图就是一种通过运用基本图形去发现、描述问题，有助于探索、发现解决问题的思路的一种直观图示。

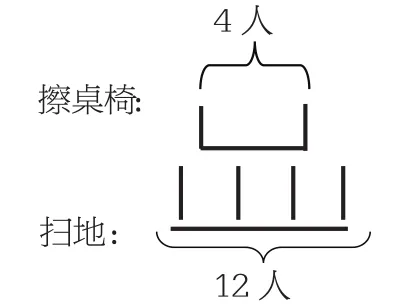
出示例题：擦桌椅的有12人，扫地的有4人，擦桌椅的人数是扫地的几倍？

师：你能用画图的方法解决这个问题吗？

展示示意图1：

擦桌椅的：︱︱︱︱ ︱︱︱︱ ︱︱︱︱

扫地的：︱︱︱︱

师：说说你是怎么想的？

生：把扫地的4人看成一份，擦桌椅的有这样的3份，那就是擦桌椅的人数是扫地的3倍。

师：其实我们还可以将示意图简化，画出线段图。

师引导画线段图理清两者之间的数量关系。

边画边说：如果用一段表示擦桌椅的人数（4人），那么扫地的有这样的几段？

12÷3＝4

答：学生的人数是老师的4倍。

这种围绕“借助直观、展示过程、启迪思维”的学习模式，帮助我们把困难的数学问题变容易，把抽象的数学问题变简单，使我们较好的理解题意，提高解题的能力。

三、简约符号直观

简约符号层面的几何直观，就是在现实生活原型的基础上进行一定的数学抽象而形成的半符号化的直观。

案例三：衣服、裤子怎么搭？

课件出示：新年到了，妈妈为敏敏准备了2件上衣，3条裤子。

师：每次上衣穿1件，裤子穿1条，一共有几种不同的穿法？

生1：4种。

生2：5种。

生3：6种。

……

师：到底有几种？谁能清楚、有序地来搭一搭？

（学生们各显神通，有借助学具摆一摆的，有用连线的方法连一连的，有用文字书写的方法写下来的。）

师：为了表述的方便，我们把2件上衣用字母A，B来表示，把3条裤子用字母a，b，c来表示。那在呈现搭配方法的时候就可以用Aa，Ab，Ac，Ba，Bb，Bc来表示。

边讲解边板书。

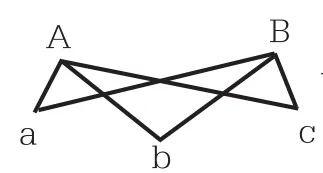
随后老师又设计了中餐一荤一素的搭配、动物园参观路线的设计安排等一系列的题目，通过学生的观察、转化、交流，使学生明白各种不同的搭配可尽可能地转化为简单的数字、字母、符号，数学就是一条“数学——几何——图形”形成的关系链。

数学低段教学中“借助几何直观进行思考”的典型案例，在发展学生的思维活动方面，不仅仅能够深化理解，而且能够培养一种独特的思维方式——凭借简捷、直观的载体，巧妙地化简问题直至化解问题。“数学是研究数量关系与空间形式的科学。”空间形式最主要的表现就是“图形”，在数学研究、学习和讲授中，我们不仅需要关注研究图形的方法、研究图形的结果，还需要感悟图形给我们带来的好处。我们要将相对抽象的思考对象“图形化”，尽量把问题、计算等数学的过程变得直观，因此，在今后的数学教学中，我们要尽量地做到：能画图时尽量画。

[1]数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]徐利治.谈谈我的一些数学治学经验[J].数学通报，2000（5）：1－4.

[3]刘晓枚.再从“几何直观谈起”[J].小学教学，2012：7-8.