“问题”去哪儿了
——记几次教学公开课的教学反思
2017-01-06南京一中明发滨江分校胡志鹏
南京一中明发滨江分校 胡志鹏
“问题”去哪儿了
——记几次教学公开课的教学反思
南京一中明发滨江分校 胡志鹏
在传统教学模式的影响下,我们在教学过程中一直关注如何提高学生分析问题、解决问题的能力,却忽视了对学生发现和提出问题的培养。“问题”究竟去哪儿了呢?笔者根据自己几次公开课的教学反思,对如何让学生发现和提出问题进行了简要探讨。
培养;课堂;提出问题;提高能力
《义务教育数学课程标准》在总目标中明确指出:“通过义务教育阶段的数学学习,学生能运用数学的思维方式进行思考,增强发现和提出问题的能力、分析和解决问题的能力。”然而一直以来,在传统教学模式的影响下,我们教师关注的重点始终是提高学生分析问题和解决问题的能力,因此,在教学中我们极力创设情境,想方设法设计问题,却忽略了学生自主发现、提出问题能力的培养。正是基于这样的思考,本学期笔者在自己的课堂中开始尝试让学生来发现问题、提出问题、设计问题。
【片段一】
在11月一次公开课(复习课)中,笔者在设计之初,打算在教学过程中安排这样一个问题,以回顾复习本章的大部分知识点。
如图1,已知,在△ABC中,点D在BC上,过点D分别作DE∥AC交AB于点E,DF∥AB交AC于点F。
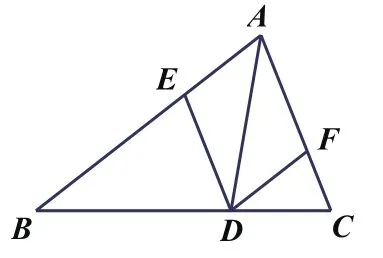
图一
(1)四边形AEDF是什么四边形?
(2)如果要得到矩形AEDF,那么△ABC应具备什么条件?
(3)如果要得到菱形AEDF,那么AD应具备什么条件?
(4)如果要得到正方形AEDF,那么AD应具备什么条件?
在磨课的过程中,师父建议将第四个问题拿掉,让学生自己在解决了第三个问题之后,自己尝试提出一个问题并解答。
师:刚刚老师给大家设计了3个问题,下面老师想请同学们自己想一想,你能不能在我们解决问题的基础上提出一个新的问题,并说说你的解决方法。
生1:△AED是等腰三角形,AD应具备什么条件?
生2:要得到正方形AEDF,那么AD应具备什么条件?
学生的回答和我们预设的并不完全一样,但这恰恰给了他们一个发现问题的机会,使得他们在课堂中思维更加活跃,问题原来一直在孩子们的脑海里。
后来在上完公开课之后,市教研员对这一设计予以了肯定,并提出了自己的设想。他说若将这个题目条件用投影打出之后,什么问题都不出示,给学生充分的空间去思考,让学生自己提出问题并解决问题,这样的设计会更加灵活,更有利于培养学生发现问题、提出问题的能力。
【片段二】
12月,笔者上了一节校内公开课“圆的复习课”,在这节课的教学过程中,设计了这样一道题:
在矩形ABCD中,AB=4cm,
BC=3cm,以A点为圆心,R为半径画圆。
若R=2cm,点P沿折线
C→D→A→B→C以1cm/s的速度移动,以点P为圆心,1cm为半径的⊙P与⊙A何时只有1个公共点?何时只有2个公共点?何时没有公共点?

师:请在这一运动情境中,提出一个考查“直线与圆位置关系”的问题,并探索你提出问题的解决方案或思路。
生1:⊙P何时与直线BC只有1个公共点?
生2:⊙P何时与直线BC只有2个公共点?何时没有公共点?
生3:⊙P何时与直线BD只有1个公共点?
学生提出的问题多好呀!生3提出的就是我们中考常考的动圆与直线相切的问题,学生自己提出的问题,有时比我们绞尽脑汁想出来的问题还要好,我们何不把机会留给学生,给他们提供一片思维的空间,“问题”原来就在这里!
【片段三】
最近,我们初三正在学习“二次函数的应用”,正巧笔者在对班里的学困生进行一元二次方程的补差,在一节课中遇到这样一个问题:
某商场销售一批衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。若商场平均每天要盈利1200元,每件衬衫应降价多少元?
师:解决了这个问题之后,你能不能对这个条件作适当的改变提出一个与二次函数最值相关的问题呢?(思考了两分钟之后)
生1:何时盈利最多?
师:能不能再具体一些?什么何时?
生2:每件衬衫应降价多少时,盈利最多?
生3:每件衬衫定价多少时,商场每天的盈利最多?
学生提出的问题恰到好处,他把一元二次方程的应用引向本节课的二次函数的应用,提出的问题也正是我们本节课研究的重点,而且这个问题很好地体现了一元二次方程和二次函数的内在联系。
提出问题对于培养学生自主学习有很大的帮助。学生的能力正是在不断地提出问题,又不断地解决问题的过程中得到提高的。在学习过程中,教师只有时刻注意培养学生的问题意识,引导学生提出问题、发现问题,让学生积极地去探索,寻找解决问题的方法,学生的思维能力才能得到提高,学生才能走上创造性学习之路。数学教学也才能够取得良好的效果,学生数学素养也必将得到全面的发展。
“问题”去哪儿了?问题就孩子的脑海里,只要我们多给学生一些机会,相信他们的思维一定能绽放出绚丽的火花!
