角动量平方算符的矢量分析计算
2017-01-06周运清黄文涛周恺元
周运清 黄文涛 周恺元
(浙江海洋大学物理系;浙江省海洋大数据挖掘与应用重点实验室,浙江 舟山 316022)
角动量平方算符的矢量分析计算
周运清 黄文涛 周恺元
(浙江海洋大学物理系;浙江省海洋大数据挖掘与应用重点实验室,浙江 舟山 316022)
量子物理是从经典物理中发展而来的,在其教学中有意识地挖掘现有教材以便与经典进行对比,指出两者的差异,并说明在什么条件下量子描述退化为经典描述,具有十分重要的教学价值,而角动量的平方算符的推导刚好提供了这样的契机. 本文利用矢量算符分析的方法来推导出在球坐标系下角动量平方算符的表达式,同时与经典的角动量平方进行了比较, 得到量子角动量平方算符比其经典对应量多出含普朗克常数的项,在经典极限下,前者退化为后者.作为拓展, 最后用Bohm规则计算了角动量平方算符.
经典物理;量子物理;角动量平方算符;球坐标系; Bohm 规则
角动量算符和角动量平方算符是量子力学中很重要的力学量,往往是学生从经典的力学量过渡到量子算符旅程中十分重要的经历之一. 对其推导进行全面的考察不仅可以得到多种推导方法,还能让学生体验物理殊途同归的乐趣,同时也能加深其过渡体验,从而深刻认识经典和量子的差异.
在经典角动量定义的基础上,现有教材文献中一般有两种推导方法得到角动量算符以及角动量平方算符. 一种是经过动量算符的代换后,利用矢量叉乘给出直角坐标系下角动量算符的分量式,然后利用直角坐标至球坐标的变换,得到球坐标系下各分量式,由平方和得到角动量平方的球坐标表达式. 计算尽管很冗长,但基本上是标量运算,概念清晰,只要仔细就行,因此在很多教材中得到采用[1,2]. 另外一种是采用矢量分析的方法来处理,即将物理量都代换成球坐标系下的算符矢量,然后经过矢量分析运算后能很快简明扼要地得到结果[3-5]. 当然也有人将这两种方法混合起来用[6],还有人采用其他方式得到结果[7,8]. 本文直接采用矢量分析来得到一般表达式,然后利用哈密顿算符和拉普拉斯算符的球坐标表达式来得到角动量平方算符表达式. 最后,将量子的表达式与经典的进行比较.
1 角动量平方算符矢量推导

根据算符运算规则,角动量平方算符可以表示成
(1)
将角动量算符代入,可得
(2)
下面利用矢量运算规则(b×c)·a=b·(c×a),来对式(2)进行变形运算,为了便于理解,我们将算符作用于一个任意函数ψ,从而得到
(3)
(4)
(5)
(6)

(7)
(8)
式(7)和式(8)代入式(5),得到
(9)
式(9)就是角动量平方算符在球坐标系下的表达式.
2 角动量平方算符在量子与经典之间的比较
为了便于比较,下面我们将经典的角动量平方表达式简单推导出来

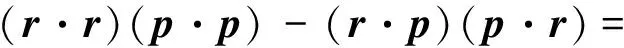
(10)

经典角动量平方也可由式(10)改写为以下等价形式:
(11)
由Bohm规则[9],也可求出相应的量子算符为
(12)
可以看出,由Bohm规则求出的式(12)与式(9)一致,但是如果把经典角动量写为
(13)
然后利用Bohm规则得到

(14)
3 结语

[1] 周世勋,陈灏.量子力学教程[M].2版.北京:高等教育出版社,2009.
[2] 赵凯华,罗蔚茵.量子物理[M].北京:高等教育出版社,2001.
[3] 冯哲川.用球坐标系推求角动量算符的本征方程[J].大学物理,1984(2):41-43.FengZC.Calculationoftheeigenvalueequationofangularmomentumoperatorbysphericalcoordinates[J].Collegephysics, 1984(2): 41-43.
[4] 王正行.从直观图像写出角动量算符的球坐标表示[J].大学物理,1987(8):7-9.WangZX.Writingouttheangularmomentumoperatorintermsofsphericalcoordinatesfromthevisualimagerepresentation[J].CollegePhysics, 1987(8): 7-9.
[5] 岑天庆.一种角动量算符的简便推导方法[J].大学物理,2010(11):26-28.CenTQ.Asimplemethodofderivatingangularmomentumoperator[J].CollegePhysics, 2010(11): 26-28.
[6] 顾樵.量子力学Ⅰ[M].北京:科学出版社,2014.
[7] 李光惠.用转动矩阵导出角动量算符的球坐标表示式[J].大学物理,1990(8):26-27.LiGH.Derivationoftherepresentationofangularmomentumoperatorinsphericalcoordinateswithrotationmatrix[J].CollegePhysics, 1990(8): 26-27.
[8] 李培廉.角动量算符的球坐标表示式的一个简易推导[J].大学物理,1983(4):7-9.LiPL.Asimplederivationofangularmomentumoperatorintermsofsphericalcoordinates[J].CollegePhysics, 1983(4): 7-9.
[9] 喀兴林.高等量子力学[M].2版.北京:高等教育出版社,2001.
■
CALCULATING THE SQUARE OPERATOR OF ANGULAR MOMENTUM BY VECTOR ANALYSIS
Zhou Yunqing Huang Wentao Zhou Kaiyuan
(Department of Physics and Key Laboratory of Oceanographic Big Data Mining & Application of Zhejiang Province,Zhejiang Ocean University, Zhoushan, Zhejiang 316022)
Quantum physics has been developed from classical physics. In the teaching process, we should be aware of digging into the existing teaching materials in order to compare with the classics, point out their difference and show under what conditions quantum description degenerates into classic description, which has very important teaching value. The derivation of the square of the angular momentum of provides the opportunity for this purpose. In this paper, the expression of the square operator of angular momentum in spherical coordinate is derived by the method of vector analysis, and then compares with the square of classical angular momentum. We obtain that in comparison with its classical counterpart, the square operator of quantum angular momentum has an extra term of Planck’s constant’s order, and in the classical limit, the quantum result is reduced to its classical counterpart. Finally, as an extension, the Bohm’s rule is used to calculate the square operator of the angular momentum.
classical physics; quantum physics; the square operator of angular momentum; spherical coordinate; Bohm’s rule
2015-08-05
浙江海洋学院科研启动项目(21065013413 ), 中青年资助项目(11062101712), 校级重大项目(X12ZD10), 浙江省自然基金项目(Y6110250, LY14A040001)和国家自然基金(11304281,31201001)资助.
周运清,男,副教授,主要从事物理教学科研工作,研究方向为量子输运和量子光合作用.yqchou@163.com;黄文涛,男,副教授,主要从事物理教学科研工作,研究方向为脑功能网络和量子光合作用.ccnuhwt@aliyun.com;周恺元,男,2013级物理学专业本科生.466812432@qq.com
周运清,黄文涛,周恺元. 角动量平方算符的矢量分析计算[J]. 物理与工程,2016,26(6):48-50.
