基于ADI格式算法的二维抛物型方程的初值问题研究*

赵瑜

(江苏食品药品职业技术学院，江苏淮安223003))

基于ADI格式算法的二维抛物型方程的初值问题研究*

赵瑜

(江苏食品药品职业技术学院，江苏淮安223003))

以二维抛物型方程为研究对象，建立交替方向隐格式的差分格式(ADI)，用追赶法分别对ADI格式的三对角线性方程组进行求解，并将该方法应用于具体算例，根据MATLAB仿真结果可知，ADI格式是一种稳定性较好，精度较高的差分格式.

二维抛物型方程;ADI格式;追赶法;MATLAB仿真

众所周知，电磁场传播、气体扩散现象、热传导过程等诸多问题都可以用偏微分方程来刻画［1］.其中，抛物型偏微分方程对于物质浓度弥散、微波热处理及电缆的输导等有着较强的应用背景［2］.一方面，诸多国内外学者致力于研究偏微分方程解的存在性与稳定性，并且获得了很多较好的结果［3－5］;另一方面，偏微分方程的数值解法也是该方向的热点问题之一，特别是对抛物型偏微分方程在有限格式的差分解法的高精度研究方面已经获得了许多有突出的结果，文献［6－8］指出Crank－Nicolson格式和向后Euler格式在解决一维抛物型方程问题时有着稳定性高、计算量小以及精度高等优点.然而，在研究抛物型方程高维条件的问题时，我们发现，向前Euler格式虽然运算过程较为简单，但对于稳定性的需求要比一维情形苛刻很多，我们通过该格式整理所得方程组已经不再是三对角线性的，而是一个大型的线性方程组，这里是针对每一时间层上的差分方程组来说的，要想求解这样的线性方程组，无论是理论推导工作还是数值计算量都是困难和巨大的.因而，构造出一种无条件的、数值计算工作量较小的、算法稳定的新的差分格式解法是非常重要的.针对求解抛物型方程的高维问题，我们的基本思想是将高维问题转换成一个个具有三对角线性特征的一维抛物问题来解决.本文将介绍一种能用追赶法计算且无条件稳定的理想算法，即ADI格式算法.

1 差分格式的建立

本文主要研究二维热传导方程的初边值问题

其中Ω=(0，1)×(0，1)，Γ为Ω的边界，且当(x，y) ∈Γ时有(x，y，0)=φ(x，y).

定义Ωh×Ωr上的网格函数U={Ukij，|0≤i，j≤m，0≤k≤n}，其中

uKij=u(xi，yi，tk)，0≤i，j≤m，0≤k≤n.

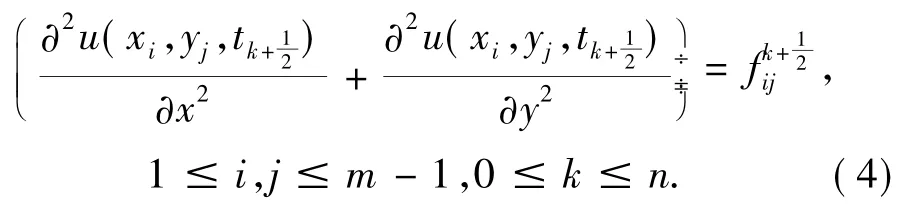
由Taylor展开式，有

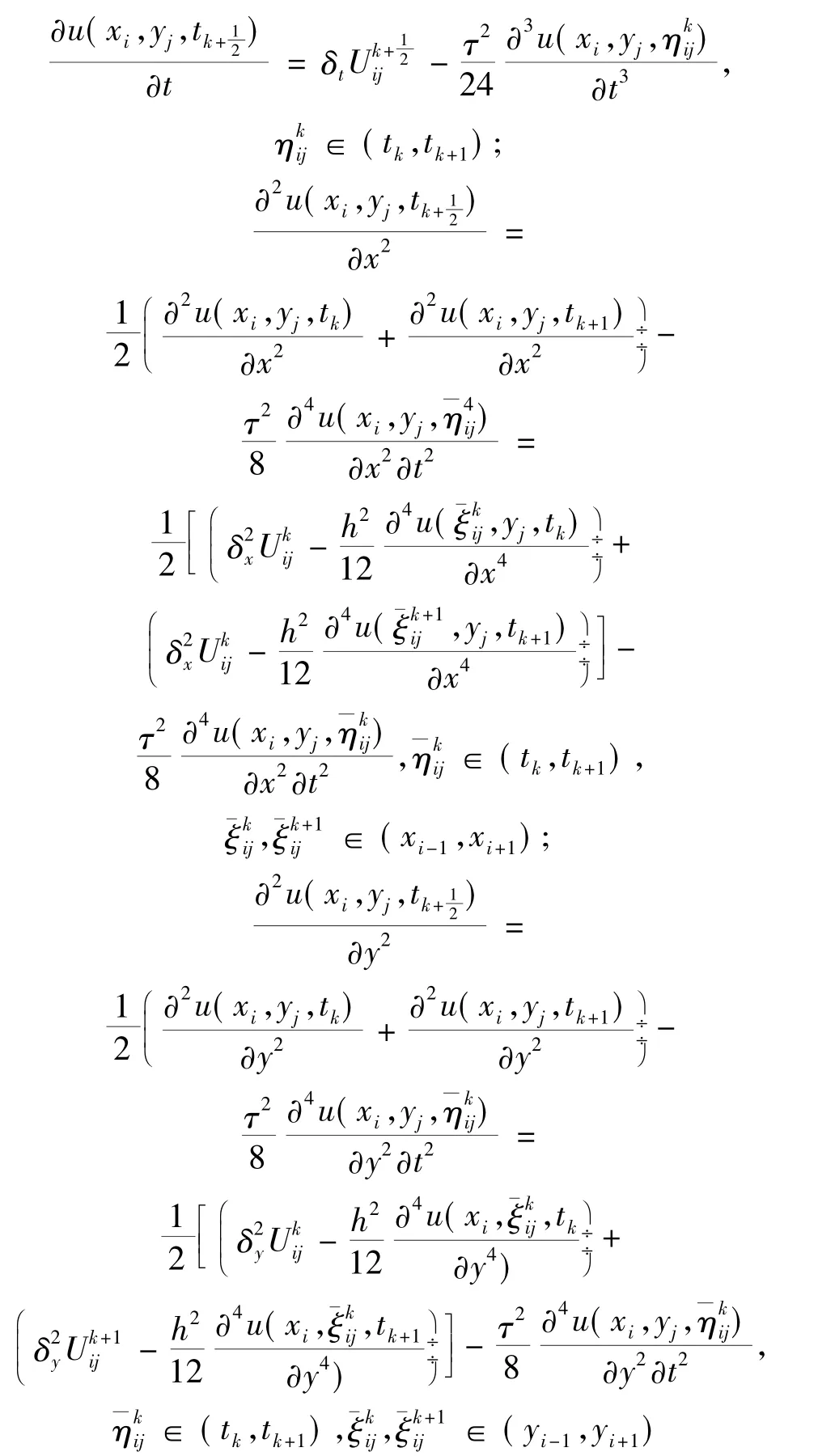
将以上三式代入(4)，得

上式又可进一步写为

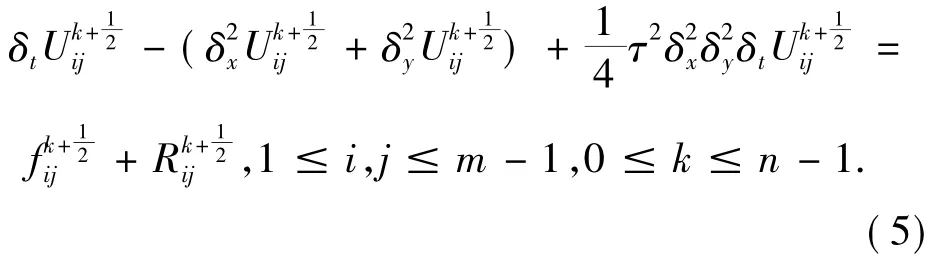
其中

2 仿真算例

计算抛物方程的二维初边值问题

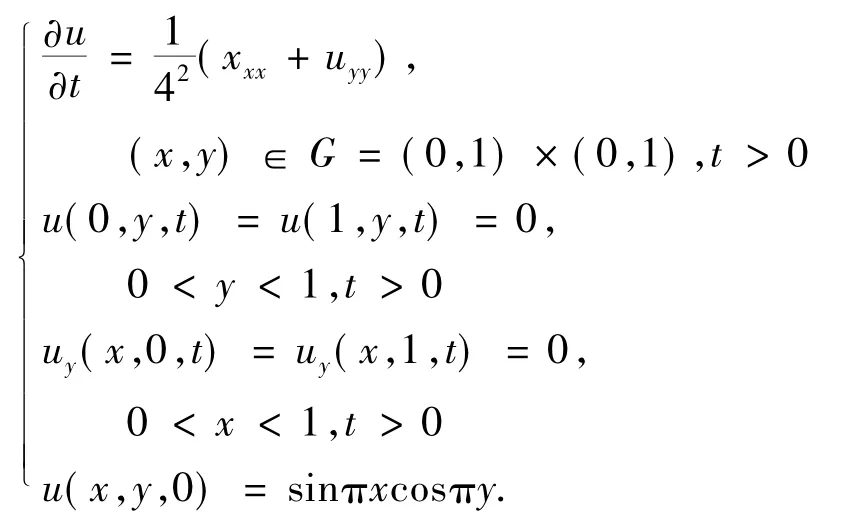
它的精确解为u(x，y，t)=sinπx cosπy exp(－.若xj=jh(j=0，1，…，J)，yk=kh(k=0，1，…，K)，tn=nτ(n=0，1，…，N)差分格式解为，则对应的初边值条件为初值条件为=sinπxjcosπyk.

若令时间分割τ=1/1600，空间分割h=h1= h2=1/40，网格剖分比r=τ/h2=1.利用ADI格式法依次运算到时间层t=1.

2.1 计算过程

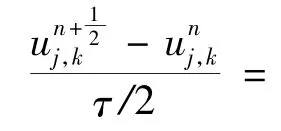
再对下面一系列三对角方程组按行采用追赶法求解:

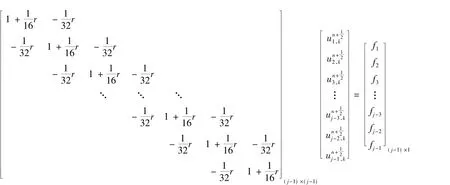
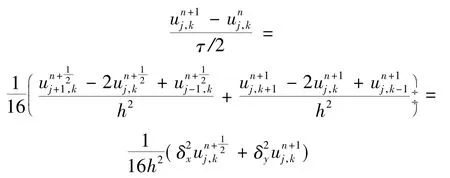
再对下面一系列的三对角方程组按列采用追赶法推导出:

2.2 求解结果

数值解图像与精确解图像分别如图1与图2所示.

O357.1

A

1008－7974(2016)06－0038－04

10.13877/j.cnki.cn22－1284.2016.12.012

2016－04－26

国家自然科学基金资助项目(11301001);江苏省“十二五”规划课题“高职数学实验课开展的研究与实践”(C－c/2013/03/039)

赵瑜，江苏泰州人，讲师.