基于概率神经网络的期货交易趋势识别及交易系统信号的优化
2017-01-05陈洋洋宋述刚
陈洋洋,宋述刚
(长江大学信息与数学学院,湖北 荆州 434023)
基于概率神经网络的期货交易趋势识别及交易系统信号的优化
陈洋洋,宋述刚
(长江大学信息与数学学院,湖北 荆州 434023)
无论是技术面还是基本面分析,都是对于市场走势的一种预测。这种预测的基础就是以原有的已经发生过的市场条件作对比,当与以往交易条件重合率达到一定程度的时候,就会认为同样的趋势会再次发生。基于概率神经网络,选取数据为大连交易所豆粕主连的日线交易数据,采用小周期交易趋势(即5交易日数据)为交易趋势基础形态,数量化各交易形态,分为9种主要交易形态,利用PNN网络进行分类识别,判断趋势的重合率为多少。试验数据结果显示分类结果良好,识别准确度达到91.67%,达到要求。利用Matlab试验结果做出程序化交易系统趋势信号指标,并根据趋势指标进行程序化的交易信号优化与决策。
概率神经网络;交易趋势识别;程序化系统优化
我国期货市场的发展从非理性逐渐向着理性方面转变,为利用技术手段进行价格测控提供了基础。在原来期货市场当中黑天鹅事件不断的发生,给投资者造成了极大的损失。在监管力度不断加强的今天,市场逐渐回归成熟与理性,使得理论有了指导实际的机会。国内外相关的学术研究日渐丰富起来。
神经网络在金融市场当中的应用主要体现在预测方面[1,2],由于金融市场的数据是非线性的时间序列数据[3],所以作为神经网络输入量的合理变换是首要解决的问题。利用由开盘价、最低价、最高价和收盘价序列经小波变换得到大尺度上逼近序列,然后进行相空间重构,得到矢量列,再构成更高维度的矢量列,作为神经网络的输入[4],恰当的处理输入量可以使网络的学习速度和精准度得到大幅度的提高。在神经网络构建方面,研究结果也在不断的丰富,其中利用RBF神经网络结构简单及良好全局逼近能力等特点[5],提出了基于径向基网格非线性时间序列的神经网络预测模型[6,7],对于短期趋势取得较好效果。对于神经网络模型的预测准确度的提高和泛化能力的提升[8,9],遗传算法的加入就显得十分的必要,Shahrokh Asadi[10]运用数据预处理技术及Levenberg-Marquardt 神经网络结合遗传算法对股票价格做出预测,在数据预处理阶段,先进行数据归一化,再选出不相关的对于预测结果有显著影响的变量,然后遗传算法寻找神经网络的初始权值[11]。对利用遗传算法做预处理结果作对比,发现对于结果准确度有显著影响。
但是神经网络应用于分类的情况不多见,文献[12]提出了神经网络应用于股市变化模式分类的方法,立足于金融市场技术分析的基点“历史是重现”,利用神经网络的模式记忆和联想的特点,将已有的数据模式作为输出变量存在网络当中,输入变量产生后,神经网络会产生相应的分类结果。对于将神经网络应用于期货市场进行分类预测的难点就在于如何合理的处理输入变量。并且将整个趋势空间分解为几种主要的趋势,是应用神经网络首先要面对的问题。因为合理的分类不仅影响着神经网络的分类结果,同时对于后面的程序化交易信号的优化也有着重要的影响。下面,笔者主要利用概率神经网络进行主要模型搭建,数据的选取为大连交易所日线豆粕主连数据,在数据的预处理方面,对于时间序列数据转化为类型输入数据,提出的自己的分类标准,并利用神经网络产生的结果,对于程序化交易系统的信号优化提出的相应准则。
1 概率神经网络
概率神经网络(Probabilistic Neural Network,PNN)是1989年由Specht提出的采用Parzen提出的由高斯函数为基函数的一种前馈型神经网络[13]。联合密度的估计方法采用的是高斯函数,并采用Bayes优化规则构造了一种概率密度分类估计和并行处理的神经网络,因此PNN具有良好了泛化能力以及较一般神经网络的快速学习能力。
1.1 PNN理论基础
Bayes决策论是解决模式分类问题的一种基本途径。Bayes决策规则有2类:一类是基于最小错误率,另一类是基于最小风险。
用X=(x1,x2,…,xd)表示一个d维特征的样本空间,Ω=(ω1,ω2,ωc)表示输出类别空间,其中c为类别总数,ωi为第i个类别。给定样本概率为p(X|ωi),则得Bayes后验概率公式为:
因此,基于最小风险的Bayes决策规则为:
∀j∈{1,2,…,c},如果p(ωi|X)>p(ωj|X),则X∈ωi(i,j=1,2,…,c,i≠j)。
如果要求最小错误率,即取得最大的p(ωi|X),因此规则为:
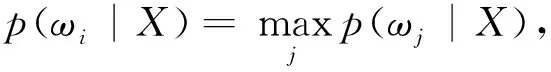
若定义θi为决策,ωj为类别,损失函数l(θi,ωj)是决策为θi、分类为ωj的损失,则在给定观测值x的条件下期望风险为:
因此,基于最小风险的Bayes决策规则为:
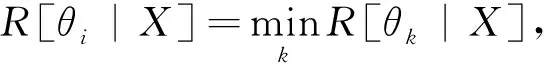
由之前的理论知识可知,需要根据先验概率p(ωi)和类条件概率密度p(x|ωi)来设计Bayes最优分类器,然而实际当中往往得不到有关问题的全部概率知识。对于先验概率一般由训练样本估计,而对于估计类条件概率密度存在较大的挑战。对于条件概率密度的估计一般有参数估计和非参数估计,参数估计最常用的为最大似然估计和Bayes估计,可以用先验知识把条件概率密度进行参数化。非参数估计法比参数估计更加实用,应用领域更加广泛。其中就包括Parzen窗估计,KN-近邻法和正交级数展开逼近法。PNN选择的方法为Parzen窗估计,高斯发展了Parzen的结论,并提出一个多元高斯函数的特例,即概率密度函数的估计为:
式中,m是训练样本中类别ω的个数;d是样本个体的特征维数;σ为平滑因子; xi为训练样本中ω类的第i个特征矢量;fω(x)是多元高斯分布在各个样本处的和,任何平滑密度函数都可以逼近。
1.2 PNN的学习算法
PNN由输入层、隐含层及输出层组成,其输出层采用竞争输出代替线性输出,各神经元只依据Parzen方法来求和估计各类的概率,由于采取竞争机制输出,因此只有一个神经元竞争获胜,则获胜的神经元表示对输入模式的分类[14]。
1)确定隐含层神经元径向基函数中心。假设训练集样本输入矩阵P和输出矩阵T分别为:
式中,pij表示第j个训练样本的第i个输入变量;tij表示第j个训练样本的第i个输出变量;R为输入变量的特征维数;K为输出变量的维数,对应K个类别;Q为训练样本数。
隐含层的每个神经元对应一个训练样本,Q个隐含层神经元对应的径向基函数中心为:
C=PT
2)阈值确定。Q个隐含神经元对应阈值为:
b1=[b11,b12,…,b1Q]′
3)隐含层与输出层权值。隐含层输出为:
ai=exp(-‖C-pi‖2bi) i=1,2,…,Q
其中, pi=[pi1,pi2,…,piR]T为i个训练样本向量。
PNN隐含层与输出层的连接权值W为:
W=t
4)输出层输出计算。连接权值确定以后,输出为:
ni=LW2,1aii=1,2,…,Q
yi=compet(ni) i=1,2,…,Q
其中,compet为Matlab中竞争输出函数。
2 PNN实现
2.1 输入变量
试验选择对象为大连交易所豆粕主连日线数据。之所以选择豆粕品种为试验对象是因为豆粕品种交易时间长,交易资金大,不易发生个人操盘事件,再就是其走势丰富,符合选入要求,可以提供充足的样本空间。
选取样本交易时间节点为2009年1月5日~2016年8月3日,单个样本容量为3300,按输入要求划分为相邻5个数据组成一个样本,样本容量为660,训练集划分为528个,测试集为132个样本。数据特征当中笔者认为重要性最高的特征为收盘价,收盘价反映了双方一天的博弈成果。输入变量为连续5日收盘价的排序及辅助的开盘价、最高价和最低价,即:
式中,t表示每根K线采集的具体时间;c代表当日收盘价;h为当日最高价;l为当日最低价;i=1,2,…,660为样本编号。
2.2 输出变量
豆粕主连收盘价走势如图1所示。收盘价格代表着市场当中所有交易者一个交易日的博弈结果,所以具有重要参考价值。收盘价在一定意义上代表着市场的趋势及交易者的态度。由图1的收盘价格时序图可以看出,市场以某一周期做有变动的重复运动,所有大的周期运动都是由小周期运动构成。价格的走势也几乎都由图2的几类走势构成。笔者主要是将9种基本趋势进行量化,送到模型当中作为输出类,供网络学习分类。
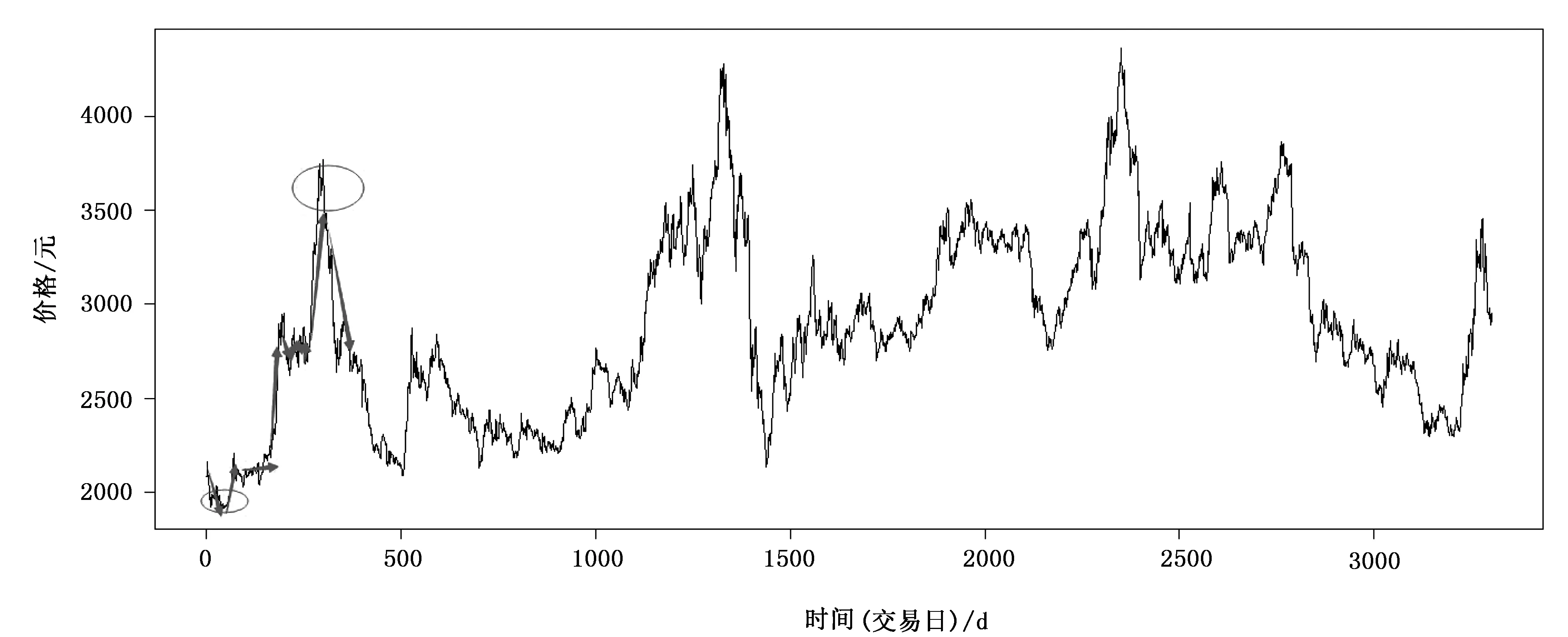
图1 豆粕主连收(交易日)盘价走势

图2 短期趋势矩阵
根据图2短暂趋势分类,可以根据Matlab中的循环判断函数进行预处理。预处理准则可以根据趋势类别进行设计,趋势类别划分越细,越能降低识别错误率。笔者提出如下的预处理准则:
1)强势上涨:ci1 2)强势下行: ci1>ci2>ci3>ci4>ci5; 3)震荡: ci1 4)上行:ci1 5)下行: ci1>ci5且ci1>min(hi(2:5)); 6)向上突破: max(li(1:4)) 7)向下突破: max(li(1:4)) 8)顶部: ci1 9)底部: ci1>ci2>ci3 在进行循环判断时,首先进行样本内部最值的获取,然后再进行判断,得到输出分类数据。 PNN试验仿真结果如表1所示,从模型结果可以看出,各类的准确率还是相对较高的。总体的预测正确率为91.67%,达到预期效果。 从分类结果来看,各类基本可以通过训练后的PNN 网络实现正确分类,但是较为明显的是每类几乎都有错分为震荡行情的情况发生,可能是由于最初分类时条件设置问题,震荡行情的限制条件较为宽松造成。从Matlab程序运行结果图可以直观的观察到分类具体情况,如图3所示。 表1 PNN试验仿真结果 注:主对角线上表示正确分类结果。 对于交易系统的开发,需要对市场有很好的理解,把握整体的趋势是整个系统的关键任务。经过PNN神经网络预测过的市场趋势,可以使市场“理解”当前市场的趋势是什么,从而做出相应的交易动作,为投资提供决策性依据。目前市场上在运行的交易系统大多为突破系统,决策信号也多为某一价格位置的突破作为入市条件,系统并无法读懂K线图或者线性图隐藏的趋势含义。如果将趋势的含义教授给系统学习,那么系统就可以作为一个单独的有学习能力的个体去完成交易任务,使整个系统更加的智能化。 PNN网络完成了趋势识别的任务,只需要将学习的结果和相应的程序化开发软件做相应对接,就可以实现程序化交易系统识别交易趋势的任务。在程序化交易系统当中,可以以下面的的标准加入系统的信号开平仓的触发条件: 1)①、②两类交易趋势,表明市场处于强势市场状态,所以如果有持仓的话,可以作为续持信号; 2)③震荡趋势表明市场没有明显趋势,这种市场状态下,最好在场外观望,不入市交易; 图4 程序交易信号流程 3)④、⑤两类虽然作为上涨和下跌趋势,但是相比于①、②来说市场相对比较犹豫,所以虽然也作为继续持有信号,但是应该相对谨慎,防止盘变发生; 4)⑥、⑦突破信号表示市场逐渐从震荡趋势当中做出选择,做出下一步走势的准备信号,也是主要的开仓信号; 5)⑧、⑨作为趋势的末端,也为之前的持仓平仓信号。 Matlab实现预设规则分类时,采用图4所示流程图实现。并且可以给每种趋势进行赋值,用来判断市场趋势的强弱,读懂K线,其具体赋值参考如下: 1)多头趋势:γ6=+1,γ4=+2,γ1=+3,γ8=-6; 2)震荡趋势:γ3=0; 3)空头趋势:γ7=-1,γ5=-2,γ2=-3,γ9=+6; 其中, γi代表相应的趋势权值;0表示市场暂无趋势;+1表示市场开始突破上行;+2表示市场确认上涨;+3表示市场开始延续强势上涨;+6意味着空头结束;-1表示市场开始显示出下跌信号;-2表示市场确认下跌;-3代表市场中下跌已成为系统势中;-6意味着多头趋势的结束。 从而可以建立趋势指标(trend index)TI,指标选取周期为3个趋势周期,即15个交易日,计算公式如下: 式中, qi代表对于第i个周期,根据PNN分类结果得到的这个周期的趋势值;βi表示对于分类结果的解读系数,βi根据神经网络判断结果取值,当周期判断为属于γi,则 βi为1,其余情况则βi为0。 计算出qi值之后,将3个周期的qi值相加就可得到TI。可以将TI指标运用于期市的各个商品主力合约之上,进行交易对象的选择,交易趋势明显的合约才能获得更多的收益,是否可以运用到股市选股当中,需要对指标进行进一步的修正及观察。 主要分析了基于概率神经网络的期货市场当中趋势的识别,区分9种主要趋势,对于市场所处状态做出合理的解读,为程序化交易信号优化提供了可能性,并创建自己新的趋势指标TI。 TI的创建使程序可以正确的解读市场当中的趋势,联系市场前后趋势状态给出更加合理的信号,并且将识别结果应用于实际的程序化交易系统的信号设计当中,取得较为理想的结果。这类应用目前还处于探索阶段,所以有很多可以进行深度研究的地方。笔者研究采用的是9类基本趋势,可以覆盖市场当中绝大多数的行情,但是市场当中还是存在很多的其他演变行情,并未划分到基本行情当中,所以需要进行趋势词典的扩充,使系统能更好的理解市场趋势。 [1] 张成虎,武博华. 基于神经网络的我国沪深股市星期效应新探 [J].西北大学学报(哲学社会科学版),2014,44(3):122~127. [2] 周开利,康耀红.神将网络模型及其Matlab仿真程序设计 [M].北京:清华大学出版社,2006. [3] 杨德平,刘喜华,孙海涛.经济预测方法及Matlab实现 [M].北京:机械工业出版社,2012. [4] 杨一文,刘贵忠.基于神经网络的多变量时间序列预测及其在股市中应用 [J].信息与控制,2001,30(139):413~426. [5] 陈政,杨天奇.基于RBF神经网络的股票市场预测[J].计算机应用与软件,2010,27(6):108~110. [6] Chang B R, Tsai H F.Composite of adaptive support vector regression and nonlinear conditional heteroscedasticity tuned by quantum minimization for forecasts[J]. Appl Intell,2007,27:277~289. [7] Clements M P, Franses P H, Swanson N R.Forecasting economic and financial time-series with non-linear models,[J]. Forecast,2004,20:169~183. [8] 许兴军,颜钢锋.基于BP神经网络的股价趋势分析 [J].浙江金融,2011(11):57~59. [9] Sitte R, Sitte J. Neural networks approach to the random walk dilemma of financial time series [J].Appl Intell,2002,16:163~171. [10] Asadi S.Hybridization of evolutionary Levenberg-Marquardt neural networks and data pre-processing for stock market prediction[J].Knowledge-Based Systems,2012,35:245~258. [11] 康璐,陈欢.基于GA-BP神经网络模型的期货价格预测与分析 [J].财经界,2011(5):108~109. [12] 叶中行,顾立庭.股市变化模式分类的两种神经网络方法 [J].上海交通大学学报.1995,29(2);100~104. [13] Specht D.Probabilistic neural network[J].Neural Networks,1990(1):9~18. [14]史峰,王辉. Matlab智能算法30个案例分析 [M].北京:北京航空航天大学出版社,2011:264~267. [编辑] 张涛 2016-06-19 陈洋洋(1989-),男,硕士生,现主要从事概率论与数理统计方面的研究工作;通信作者:宋述刚,教授,2712281782@qq.com。 O21;TP183 A 1673-1409(2016)31-0013-07 [引著格式]陈洋洋,宋述刚.基于概率神经网络的期货交易趋势识别及交易系统信号的优化[J].长江大学学报(自科版),2016,13(31):13~19.3 试验结果与分析

4 程序交易系统信号优化
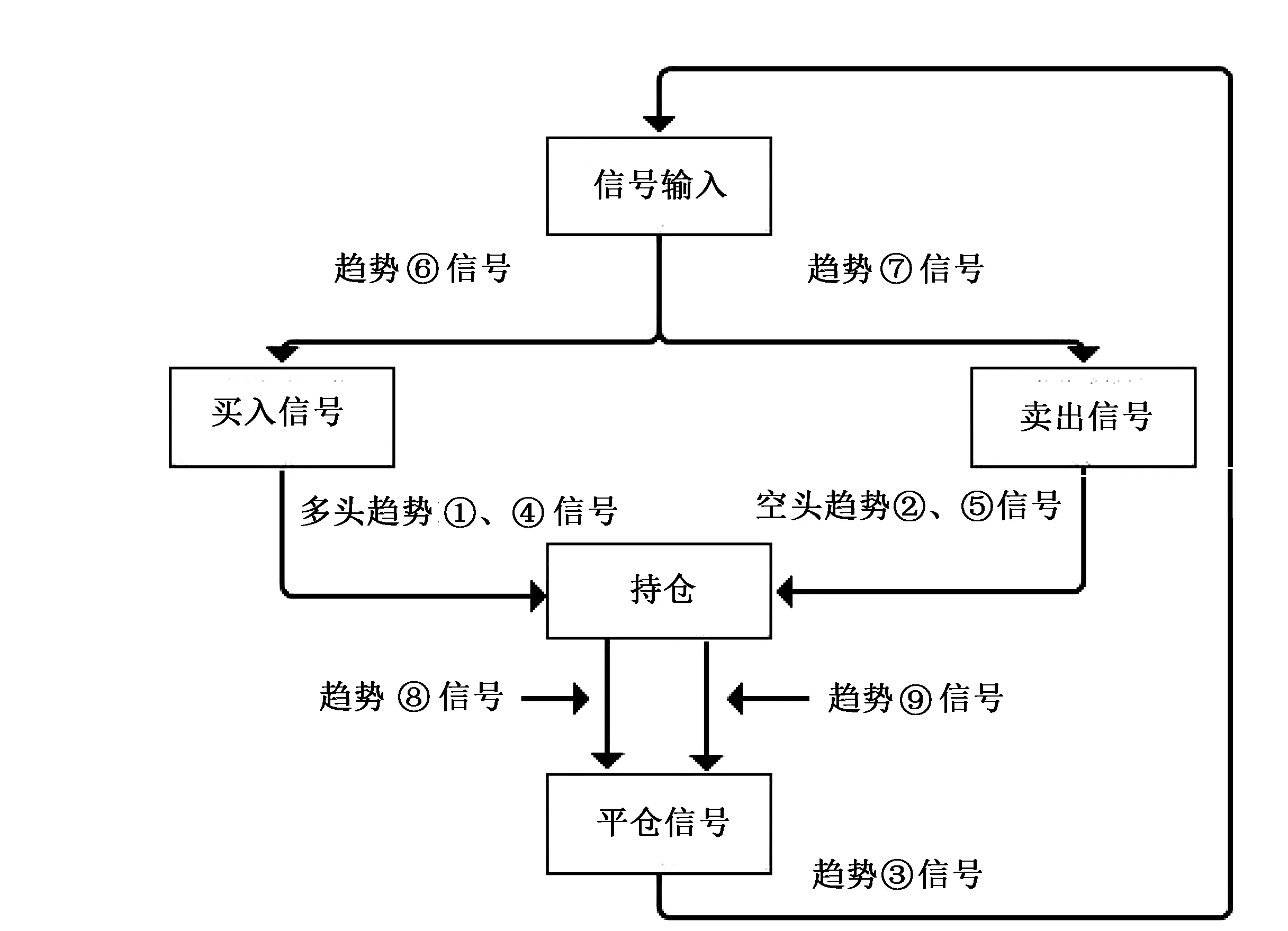
5 结语
