四元同名元素不相邻可重复排列数的算法

史千里

(长江大学文理学院，湖北 荆州 434020)

四元同名元素不相邻可重复排列数的算法

史千里

(长江大学文理学院，湖北 荆州 434020)

研究四元同名元素不相邻可重复排列数F(a,b,c,d)的一般性质，获得了排列数F(a,a,a,a)和F(a,a,c,d)的递推公式以及F( 1,1,c,d)的计算公式。

可重复排列；同名元素不相邻；序串

定义1设a+b+c+d=n，a,b,c,d∈Z+,a≤b≤c≤d，φ是有序串，令:

S ={φ∣φ=x1x2，…xn,φ含a个A, b个B, c个C, d个D,不含片断AA、BB、CC、DD}

其中，φ是四元同名元素不相邻可重复排列，令F(a,b,c,d) =∣S∣，即为排列数。

如1个主持人、1位嘉宾、3名老师和3名学生坐成一横排，同身份的人不相邻，求不同的排法数。

对于三元同名元素不相邻可重复排列数F(a,b,c)(1≤a≤b≤c )，文献[1]给出了的递推公式。 四元同名元素不相邻可重复排列数F(a,b,c,d)还没有一般的算法,已有研究仅限于极特殊的个例情形[2],而这类计算又有着很重要的应用[3]。为此，笔者在获得F(a,b,c,d)的部分一般性质基础上，求得多种情形的递推公式或计算公式。

令：

SA={ψ│ψ∈S,ψ左端x1≠A}

记：

|SA|=A(a,b,c,d)

可以类似地定义|SB|=B(a,b,c,d)，|SC|=C(a,b,c,d)，|SD|=D(a,b,c,d)。

定理1设1≤ a ≤ b ≤ c≤ d。则F(a,b,c,d)≥1的充分必要条件是:

d-1≤a+b+c

(1)

证明 (必要性)设F(a,b,c,d)≥1，即S≠φ, 设φ∈S，φ含d个D, 至少需要d-1个A、B、C才能使φ中没有DD片断，所以d-1≤a+b+c。

(充分性)设式(1)成立。只需构造一个φ∈S，则可得F(a,b,c,d)≥1。

先排a个A, b个B, c个C：

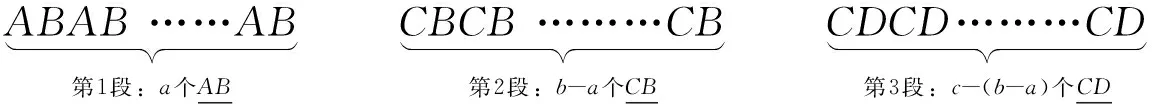
还剩余d-[c-(b-a)]=d+b-(a+c)个D。

第1段和第2段共有[a+(b-a)]×2-1=2b-1个“缝”可以插入D, 第1段开头左侧、第2段尾部右侧可以各排1个D。于是，共有(2b-1)+2=2b+1个空位可以排D。由式(1)知：

(2b+1)-[ d+b-(a+c)]=(a+b+c)-(d-1) ≥0

所以，在第1,2,3段上可以把剩余的D排尽,即∃φ∈S。

推论1设1≤a≤b≤c≤d,恰在a+b+2种情形下F(a,b,c,d)≥1，即:

F(a,b,c,c+j)≥1 j∈{0,1,2, …，a+b,a+b+1}

易证得以下6个引理。

引理1F(0,b,c,d)= F(b,c,d)。

F(b,c,d)的定义和算法见文献[1]。

引理2A(0,b,c,d)=F(b,c,d)

引理3A (a,b,c,d) =A(a,c,b,d)=…

=B(b,a,c,d)=B(c,a,b,d)= …

=C(c,b,a,d)=C(b,c,a,d)=…

=D(b,c,d,a)=D(c,b,d,a)=…

引理4A(a,0,c,d)=A(a,c,0,d)=A(a,c,d,0)=A(a,c,d)

A(a,c,d)的定义和算法见文献[1]。

引理5A(a,b,c,d)= B(a,b-1,c,d)+C(a,b,c-1,d)

+D(a,b,c,d-1) (1≤a,b,c)

引理6F(a,b,c,d)= A(a-1,b,c,d)+B(a,b-1,c,d)

+C(a,b,c-1,d)+D(a,b,c,d-1) (a,b,c≥1)

由引理5和引理6即得定理2。

定理2设a≥1，则:

A(a,b,c,d) = F(a,b,c,d)-A(a-1,b,c,d)

推论2A(1,b,c,d)=F(1,b,c,d)- F(b,c,d)

定理3若d=a+b+c+1,则：

(2)

定理4设a≥1, 则:

F(a,a,a,a)=12A(a-1,a-1,a,a)

(3)

设a≥2, 则:

F(a,a,a,a) =12[A(a-2,a-1,a,a)+4A(a-2,a-1,a-1,a)+6A(a-2,a-1,a-1,a-1)]

(4)

证明由引理1～引理6得:

F(a,a,a,a) =A(a-1,a,a,a) +B(a,a-1,a,a) +C(a,a,a-1,a) +D(a,a,a,a-1)

=4A(a-1,a,a,a)

=12A(a-1,a-1,a,a)

=12[A(a-2,a-1,a,a)+2A(a-1,a-1,a-1,a)]

其中:

A(a-1,a-1,a-1,a)=2A(a-2,a-1,a-1,a)+A(a-1,a-1,a-1,a-1)

A(a-1,a-1,a-1,a-1)=3A(a-2,a-1,a-1,a-1)

代入即得式(4)。

定理5设1≤a=b≤c≤ d，d-1≤ a+b+c，则:

F( a,a,c,d) = 2A(a-1,a, d-c) +F(a,a,d-c)-2A(a-1,a,c,d)

+A(a-1,a,c-k,d-k+1)+A(a-1,a,c-k+1,d-k)]

(5)

证明由引理1～引理6得:

F(a,a,c,d) =A(a-1,a,c,d) +B(a,a-1,c,d) +C(a,a,c-1,d) +D(a,a,c,d-1)

=2A(a-1,a,c,d) +C(a,a,c-1,d) +D(a,a,c,d-1)

=2A(a-1,a,c,d)+[A(a-1,a,c-1,d)+B(a,a-1,c-1,d)+D(a,a,c-1,d-1)]

+[A(a-1,a,c,d-1)+B(a,a-1,c,d-1)+C(a,a,c-1,d-1)]

=2A(a-1,a,c,d) +2A(a-1,a,c-1,d) +2A(a-1,a,c,d-1)

+4A(a-1,a,c-1,d-1)+2A(a-1,a,c-2,d-1)+2A(a-1,a,c-1,d-2)

+4A(a-1,a,c-2,d-2)+2A(a-1,a,c-3,d-2)+2A(a-1,a,c-2,d-3)

+C(a,a,c-3,d-3) +D(a,a,c-3,d-3)

= ……

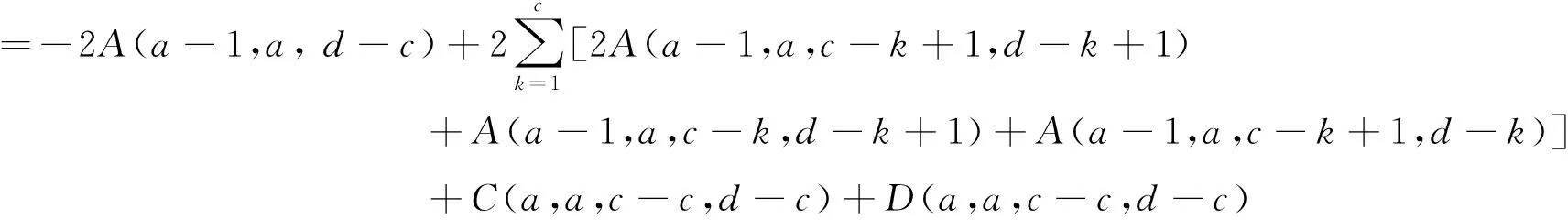
其中：

C(a,a,c-c,d-c)=C(a,a,0,d-c)=F(a,a,d-c)

D(a,a,c-c,d-c) =D(a,a,0,d-c)=A(a-1,a,0,d-c)+ B(a,a-1,0,d-c)

=A(a-1,a,d-c)+ B(a,a-1,d-c)

=2A(a-1,a,d-c)。

代入即得式(5)。

由推论1知，F(1,1,c,d)共有4种情形：d=c,c+1,c+2,c+3。定理6和定理7分别给出了算法。

定理6设c≥1 , 则:

F( 1,1,c,c)=20c2+4

(6)

证明由定理5得:

F(1,1,c,c) =2A(0,1, 0)+F(1,1,0)-2A(0,1,c,c)

=2×1+2!-2F(1,c,c)

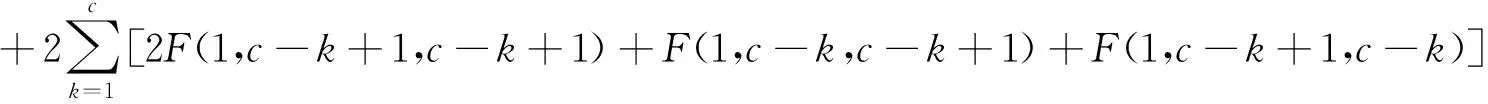
由文献[1]定理5得:

F(1,c,c)=6c

F(1,j,j)=6j

F(1,j-1,j)=4(j-1)+2=2(2j-1)

所以:

定理7设c≥1, 则:

F(1,1,c,c+1)= 15c2+15c+6

(7)

F(1,1,c,c+2)=6(c+1)2

(8)

(9)

证明设d-c=t≥0，由定理1知，当且仅当t=0,1,2,3时，F(1,1,c,d)≥1。由定理5得:

F(1,1,c,d) =2A(0,1, t)+F(1,1,t)-2A(0,1,c,c+t)

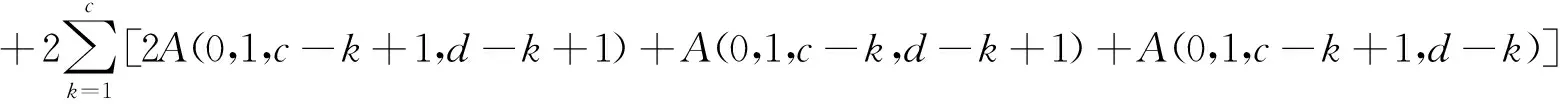
=2F(1, t)+F(1,1,t)-2F(1,c,c+t)

t=1时:

F(1,1,c,c+1)=2F(1, 1)+F(1,1,1)-2F(1,c,c+1)

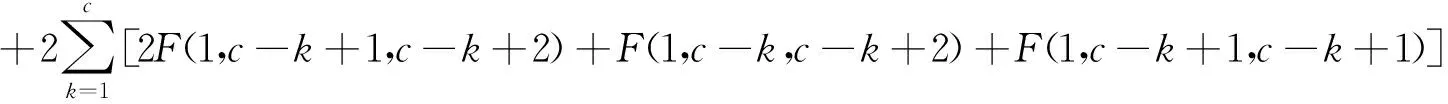
由文献[1]定理5得:

F(1,c-k+1,c-k+1)=6(c-k+1)

F(1,c,c+1)=4c+2

F(1,c-k+1,c-k+2)=4(c-k+1)+2

由文献[1]定理2得:

F(1,c-k,c-k+2)=c-k+1

所以:

= 15c2+15c+6

t=2和t=3时,可以类似地证明式(8)和式(9)。

[1]史千里.一个特殊可重复排列数的算法[J].数学的实践与认识，2009, 39(5):207～211.

[2] 仇索.抽空法：“不相邻”排列问题的专项工具[J].数学通讯,2014(Z3):69～71.

[3] 钟集.若干相同元不相邻的重复n排列的计算及应用[J].华东理工大学学报(社会科学版),1997(3):1～5.

[4] 孙淑玲，许胤龙. 组合数学引论[M]. 合肥: 中国科学技术大学出版社, 1999.

[编辑] 张涛

2016-07-28

湖北省教育厅科研技术项目(B2014281)。

史千里(1963-)，男，副教授，现主要从事数论和高等数学方面的教学与研究工作；E-mail:bamsky@126.com。

O157

A

1673-1409(2016)31-0005-04

[引著格式]史千里.四元同名元素不相邻可重复排列数的算法[J].长江大学学报(自科版)，2016,13(31)：5～8.