主成分聚类分析法在数学中文核心期刊综合评价中的应用

刘莲花

(海南医学院公共卫生学院，海南 海口 571199 )

主成分聚类分析法在数学中文核心期刊综合评价中的应用

刘莲花

(海南医学院公共卫生学院，海南 海口 571199 )

指出了目前主成分分析法在期刊综合评价中的误用情况，并采用主成分分析法对17种数学中文核心期刊进行了综合评价，当第一主成分方差贡献率不够时，采用了主成分聚类分析法进行排名，给出了第一主成分、综合主成分及主成分聚类法的排名，最后分析了主成分聚类方法的有效性。

主成分聚类分析；综合评价；数学期刊

学术期刊评价是通过对学术期刊的发展规律和增长趋势进行定量分析以反映期刊的学术水平与影响力，为优化学术期刊的使用与科技评价提供重要参考，同时可以提高学术期刊的内在质量，促进学术期刊的健康成长和发展。因此，客观公正地对学术期刊进行评价，反映学术期刊的真实水平与影响力越来越受到学者们的重视。

目前，国内不少学者将主成分分析法[1～3]、因子分析法[4]、属性识别法[5]等综合评价方法应用于科技期刊评价中，其中主成分评价方法应用得最多，但不少文章存在误用的情况，如没有进行主成分分析适用性检验，反向指标没有进行正向化处理，还有的误将因子得分当成主成分得分等。并且利用主成分分析法进行期刊综合评价时，大部分学者都是利用综合主成分得分进行综合评价，然而数理统计学界一般都主张采用第一主成分进行综合评价，如孟生旺[6]从几何投影角度阐明在多指标综合评价中只有第一主成分综合原始数据的信息最多；苏为华[7]认为只有第一主成分才是揭示“评价信息”，其他主成分只是“形态因子”，不具有综合评价功能；徐雅静[8]、张虎[9]、王学民[10]等也都认为只能用第一主成分进行综合评价。因此，在用主成分方法进行期刊综合评价时，应该只采用第一主成分得分进行评价。徐雅静还提出如果第一主成分方差贡献率不够高，可采用“主成分聚类分析法”进行综合评价。鉴于以上分析，笔者对17种数学中文核心期刊采用主成分聚类分析法进行了综合评价，并与第一主成分和综合主成分排序结果进行比较，希望能对提高数学期刊的综合质量有所帮助。

1 研究对象和统计指标

以《中文核心期刊要目总览》(2012年版)刊登的17种数学中文核心期刊为对象，以科学技术文献出版社《2013年版中国期刊引证报告(扩刊版)》[11]提供的7项计量指标为原始数据进行分析评价。该7项指标的含义如表1所示，具体数据如表2所示。

2 数据预处理

1)指标的正向化[12]。因为被引半衰期x6是反向指标，采用倒数化进行正向化处理，正向化后的指标设为y6。

2)指标的标准化。为了消除原始数据数量级和量纲的差异，将原始数据进行标准化，标准化后的变量记为zi。

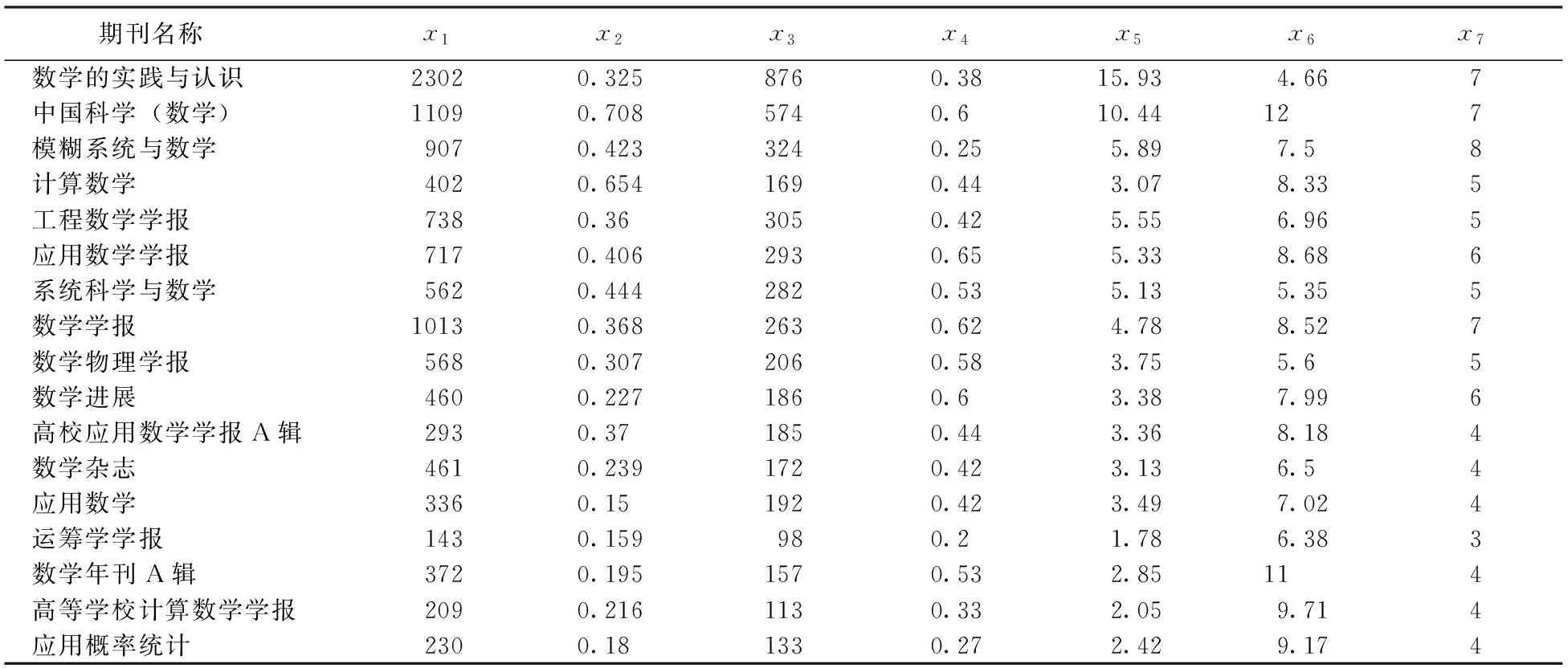
表2 17种数学核心期刊的7项计量指标原始数据

3 主成分分析

进行主成分分析首先要进行KMO和Bartlett检验，KMO取值在0～1，该值越大，表明数据越适合做主成分分析，且一般要求该值大于0.5。研究中采用SPSS19.0进行检验，KMO值为0.651，符合主成分分析要求，且Bartlett检验的显著性水平远小于0.05，所以说明相关矩阵不是单位阵，2种检验结果都表明原始数据适合于进行主成分分析。

利用SPSS 19.0的Factor Analyze 进行分析，通过计算，可得各指标相关系数矩阵的特征值和方差及累计贡献率，如表3所示。由表3可知，前3个主成分累计贡献率为88.327%，根据累计贡献率大于85%的原则，故选取前3个主成分。其初始因子载荷如表4所示，将表中的每一列向量除以其对应的特征值的平方根，就得到相应的主成分的系数向量。

利用主成分系数，可得各主成分表达式如下：

F1=0.484z1+0.274z2+0.484z3+0.143z4+0.484z5+0.179z6+0.412z7

(1)

F2=-0.153z1+0.486z2-0.133z3+0.536z4-0.133z5-0.598z6+0.243z7

(2)

F3=0.014z1-0.301z2-0.067z3+0.819z4-0.067z5+0.458z6-0.140z7

(3)

取前3个主成分各自的方差贡献率为权重，可得综合主成分表达式如下：

F=0.56265F1+0.22115F2+0.09948F3

(4)

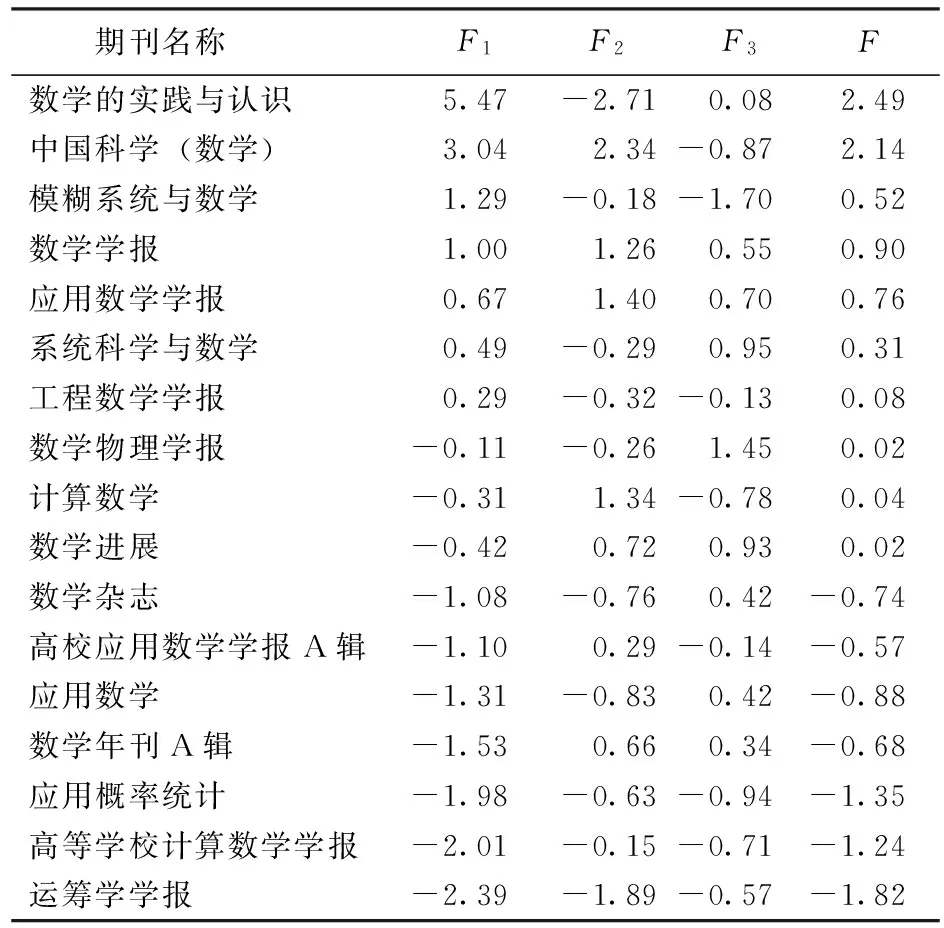
表5 前3个主成分得分及综合得分

将各期刊标准化后的数据带入式(1)～(4)，即可得每种期刊的前3个主成分得分和综合主成分得分，如表5所示。

4 主成分聚类方法与结果分析

因为第一主成分方差贡献率仅为56.265%，一般只有当第一主成分贡献率较高(85%以上)时，才可以仅按第一主成分得分进行综合排序评价，否则会有片面性，此时可以将主成分分析与聚类分析2种统计方法结合起来，采用“主成分聚类分析法”。聚类分析是将样品或变量按照它们性质上的亲疏相似程度进行分类的一种方法，这样通过聚类分析就可以将期刊按照它们的相近程度进行分类，但是并不能得到各类优劣程度的排序。主成分聚类即先主成分分析，再取若干主成分对样品进行聚类分析，然后结合第一主成分得分对样品进行分类排序，由此得到一种新的综合评价方法，具体步骤如下：

1)按照累计贡献率选定前r个主成分，计算主成分得分；

2)对选定的主成分矩阵(F1，F2，…，Fr)进行系统聚类分析；

3)计算各类中第一主成分得分的平均值确定类间排序；

4)根据类中各样品的第一主成分，确定每类中样品排序，得到综合排序。对表5中的3个主成分得分矩阵(F1，F2，F3)进行系统聚类分析，聚类方法采用最小方差法，距离度量选择欧式平方距离。聚类结果如下：

第1类：数学的实践与认识；

第2类：中国科学、模糊系统与数学；

第3类：数学学报、应用数学学报、系统科学与数学、工程数学学报、数学物理学报、数学进展；

第4类：计算数学、高校应用数学学报A辑、数学年刊A辑；

第5类：数学杂志、应用数学、应用概率统计、高等学校计算数学学报、运筹学学报。

进一步按主成分聚类方法进行类间与类内排序，最终主成分聚类排名和第一主成分及综合主成分排名如表6所示。

表6 各种方法的综合评价排序结果

从表6可知，基于第一主成分分析的综合排名与基于主成分聚类分析法的综合排名比较接近，而综合主成分排名的差异则较大。如无论按照第一主成分方法还是主成分聚类分析法排名，模糊系统与数学的排名都在数学学报的前面，但是综合主成分排名却相反，观察原始数据可以看出，模糊系统与数学在5个指标方面都优于数学学报，只有“总被引频次”和“学科影响指标”低于数学学报，理应排在数学学报的前面，数学物理学报和计算数学也是类似的情况，因此进一步说明了综合主成分排名是不合理的。第一主成分分析排名与主成分聚类分析排名在计算数学与数学进展这2种期刊上的排名有差异，分析原始数据发现数学进展在5项指标上都优于计算数学，理当排在计算数学之前，同理，高校应用数学A辑也应排于数学杂志之前。也即用主成分聚类分析方法所得的排名比用第一主成分分析方法所得的排名更加合理。

5 结语

采用主成分分析法对17种数学中文核心期刊进行了综合评价，并且当第一主成分方差贡献率不够时，采用了主成分聚类分析法进行排名。结果表明，利用主成分聚类方法进行期刊综合评价是行之有效的，具有科学性和可操作性。

[1]张弘，赵惠祥，刘燕萍，等.基于主成分分析法的科技期刊评价方法[J].编辑学报，2008,20(1)：87～90.

[2] 辛督强.基于主成分分析的13种力学类中文期刊综合评价[J].中国科技期刊研究,2012,2(2)：224～227.

[3] 李红.基于主成分分析法的上海科技期刊排序研究[J].中国科技期刊研究,2009,20(1)：57～62.

[4] 辛督强，韩国秀.因子分析法在科技期刊综合评价中的应用[J].数理统计与管理，2014,33(1)：116～121.

[5] 林春艳, 莫琳. 自然科学学术期刊质量指标体系的属性数学综合评价模型[J].数学的实践与认识,2004,(5):1～7.

[6] 孟生旺.用主成分分析法进行多指标综合评价应注意的问题[J].统计研究，1992，(4):67～68.

[7] 苏为华.多指标综合评价理论与方法问题研究[D].厦门大学，2000.

[8] 徐雅静，汪远征.主成分分析应用方法的改进[J].数学的实践与认识，2006,36(6)：68～75.

[9] 张虎，刘吉普.主成分分析方法用于系统评估的若干问题研究[J].统计与决策，2009，(13)：11～13.

[10] 王学民.对主成分分析中综合得分方法的质疑[J].统计与决策，2007，4:31～32.

[11] 中国科学技术信息研究所. 2013年版中国期刊引证报告(扩刊版)[M].北京：科学技术文献出版社，2013.

[12] 俞立平，潘云涛，武夷山.学术期刊综合评价数据标准化方法研究[J].图书情报工作，2009,53(53)：136～139.

[编辑] 张涛

2016-07-27

海南省教育厅科学研究项目(Hnky2016-30)。

刘莲花(1983-)，女，硕士，讲师，现主要从事综合评价理论及应用方面的研究工作;E-mail：26734799@qq.com。

O212

A

1673-1409(2016)31-0009-04

[引著格式]刘莲花.主成分聚类分析法在数学中文核心期刊综合评价中的应用[J].长江大学学报(自科版)，2016,13(31)：9～12.