也谈光散射增强

程光煦

(南京大学固体微结构物理国家实验室及物理系,南京 210009)

也谈光散射增强

程光煦

(南京大学固体微结构物理国家实验室及物理系,南京 210009)

“增强”是上世纪七十年代,在(非弹性)光散射中发现的重要现象之一。在过去几十年中,人们锲而不舍投入了大量的时间和经费,时至今日,已有各种机制来说明或解释它,但仍不尽人意。十余年来,超高“增强”(g是增强因子～1014-15)的报导更是将它推向一新的境地,原有的想法遇到了莫大的障碍和挑战,必须用新的思想(格林函数的“极”或散射截面)考虑、处理这类问题。本文除了讲述非弹性光散射光强的基础知识之外,还给出了过往未能理解和阐述的内容,如分形、极化、纳米、准相位匹配和单分子层界面等结构的增强,为该领域的工作提出了新的方向和路径。

(非弹性)光散射；增强

1 引言

非弹性光散射的拉曼散射谱中最基本的两个特征量是频移(ωs=ωL-ωq;ωΑS=ωL+ωq)和散射光光强(IS,IAS)。长期以来人们对前者,即频移较为重视,也完成了不少工作,而对散射光强的关注、研究显得苍白无力、淡漠冷清；其中不乏片面、错误的认识,如光散射增强斯托克斯、反斯托克斯分量及它们的比值等物理量,对于不同材料随外界条件(如激光的功率,温度,配置等)的变化有截然不同的结果。特别是在增强因子的测定中,违背常识的错误还作为成果宣传、引用。曾经还成立过表面增强专业分会,多年来花费不少的人力、经费和时间,由此可见人们对它的兴趣和重视。

“增强”是上世纪七十年代在光散射(特别是非弹性光散射)中发现的重要现象之一。时至今日,有各种机制(如化学、物理、电磁场等)来说明或解释它。十余年来,超高(g～1014-15)增强因子的提出更是将它推向一新的境地[1],必须用新的思想考虑(格林函数中谱的“极”或散射截面)、处理这类问题。

本文除了讲述非弹性光散射的光强基础知识外,还给出了过往未能理解和阐述的内容,即分形、极化、纳米、准相位匹配和单分子层界面的增强。不得不指出的是表面增强拉曼(SERS)应改成“光散射增强”,原因是：(1)“增强”不仅仅发生在表面,对于体内结构也有该现象,对不同的材料、结构表面的尺度标准相差甚远；(2)不仅拉曼散射过程出现“增强”,在其它光与物质作用过程中也有“增强”,如红外、荧光、二次谐波、和频等光谱中都存在该现象,因而产生的增强光谱学(Enhanced Spectroscopy)极大地丰富了该领域的研究内容和深度；(3)多波(矢)互作用中有倒格矢参与的过程中也有“增强”,其中不再是“增强”因子的变化,而包含更深的光与物质作用过程和物理内容。

本文部分内容虽已在18th全国光散射学术会议(物理分会)邀请报告上给出,但终因时间短,概念、内容多,未讲完。现给出全部内容,即增强机制(如热位、热点、激活元等)、散射截面(估量)、单分子层、纳米(自相似,纳米透镜等)、波罗德定律、(准)相位匹配增强、光谱格林函数、光谱的“极”、狄义赫利-诺伊曼条件(这两部分内容可不阅读,不影响对全文的理解)、实测的可能(靠)性,最后给出明确的结论。

2 简况

2.1 光散射增强的发现

在上世纪七十年代中期,M.Fleischmann、R.P.Van.Dunye和J.A.Creighton各自独立地在吡啶(pyridin)中发现“增强”现象[2-4]。随后,在若丹明(Rhodamine 6G)中也发现“增强”。在三十年前A.Otto,K.Arya和R.Zeyher虽给出了经典的理论解释[5](surface-enhanced Raman scattering “classical” and “chemical” origins和theory of surface-enhanced Raman scattering ),但仍不能满足现今的需要。欣慰的是,近期又有关于表面增强的专著[6]给出相应物理阐述,指出了该领域的研究方法和途径。

2.2 光强

拉曼散射中,斯托克斯(S)和反斯托克斯(A)分量的光强分别为：

(1)

(2)

式中p表示三种微观粒子的分布:即玻色-爱因斯坦分布、玻尔兹曼分布和费米-狄拉克分布。式中q表示某种元激发,如声子,极化激元,磁振子,电子空穴对,极化子,配偶子等。

三种分布的斯托克斯拉曼散射强度分别为：

(3)

三种分布的反斯托克斯拉曼散射强度分别为：

(4)

(3)、(4)表达式中比例常数C都已略去：

IB-E表示参与元激发是以集体激发为主的玻色子(如：声子、极化激元、磁振子等)的散射光强。

IBoL表示参与元激发满足玻尔兹曼分布(如：分子、原子等)的散射光强。

IF-D表示参与元激发是以个别激发为主的费米子(如：电子、极化子、电子 - 空穴对等)的散射光强。

三种分布的斯/反斯的强度比分别为：

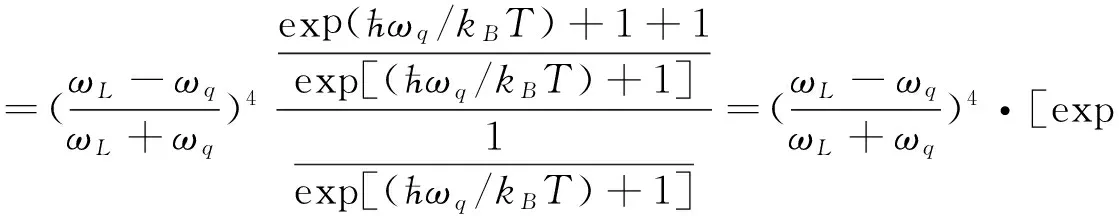
问津该工作的人不多,这是因为涉及到以下的问题：(1)长期以来,人们只将斯托克斯分量的光强作为标识特征,已约定俗成,对反斯托克斯分量的考量不多；(2)该比值究竟能提供哪些信息,其随外界条件的改变,如何变化、深究的更不多；(3)实验上尚存难以解决的问题,如：调节到最佳状态后,如何保持所用的激光功率在采集数据过程维持在同一标准；并不是所有物质的反斯托克斯散射都会出现在光谱仪上；(4)对光散射量子过程(三能级、两光子和一个元激发的作用过程)的理解不够;(5)边界与界(介)面的理解、认知尚存差异(图1、2) 。

Fig.1 A living example of interface,there are clear differently material layer[7]

Fig.2 A few kinds boundaries,TCCB is most importance sort of them,for new materials[8]

图1是典型的几种材料构成的平整、规则的界面,它能很好的满足狄义赫利-诺伊曼(表、界面)条件。图2中的TCCB是由位错↔旋错形成的结构,其作用等效三棱镜,由三个晶介边构成“棱边”,且垂直于纸面。

斯托克斯和反斯托克斯强度比有不少问题有待探究,如：用拉曼散射强度比确定膜厚度、用拉曼散射强度比确定稀磁半导体载流子浓度等,已被人们掌握应用；斯托克斯分量与反斯托克斯分量的比值又会为我们提供哪些信息,应该去研究。

2.3 光强表达式

(1)对自由取向分子系统拉曼散射强度为：

exp[-E(v,l,n)/kBT]·I0

(5)

式中的I0为激发光光强；σ(ω)m→l为频率ω下的散射截面；E1为初态能级; kB,T分别是玻尔兹曼常数和室温；N为参与散射的分子数；gS为统计权重因子；J为角量子数；Z为配分函数,即态和。式中

Z=σ(ω)m→l·gS·(2J+1)·

exp[-E(v,l,n)/kBT]

(2)对90°散射双原子旋转拉曼散射强度为：

(6)

式中的N,I0与(1)中情况相同；而

(3)不透明固体拉曼散射光强

(7)

式中,c为检测器效率与单色仪带通之积(0.1～0.5),f(θ)为光散射系统对散射光收集率,F0为激光光通量,R为样品前反射系数,α为光吸收系数,l为光穿透深度；σ为散射截面。

(4)多层膜的拉曼散射光强

I=c·f(θ)·F0·(1-R2)·

(8)

(8)式中di为第i子层厚度,dT为每一周期层厚度,DR为总厚度,DR=Z·dr,ni为第i子层的折射率(其它参数与公式(7)相同)。

3 增强机制

3.1 截面单分子增强

长期以来,人们对表面增强(SERS)的增强因子认知不深或不妥。低估它们和常温拉曼散射之间的异同,不知道究竟有多少分子、原子、粒子或元激发参与了增强过程。为回避该问题,人们创建了各种不同的方法,如在该过程的斯托克斯和反斯托克斯散射用到了有效截面的信息。对非常强的拉曼散射能测到除热(分布)布居数外,还有第一振动能级的布居数,振动抽取(泵浦)过程的有效拉曼散射截面,即由(斯/反斯)信号比的玻尔兹曼布居数偏离中得到。有效共振增强散射截面增强因子远超以往的数值(103～105),声称能高达到1014～1015[9-11],如银胶SERS散射截面为σ ～ 10-16cm2,比正常拉曼散射的截面为σ ～10-30cm2的数值高1014倍,即增强了1014倍。必须指出的是：增强1014倍并不是实际测量到的数值,仅是由散射截面比对得到的数值。

3.2 单分子增强谱实测装置

图3装置中给出的激发能量是红外范围(以避免荧光信号的激发)；右下图中每个金聚集体(～200 nm)中含有8～10个金纳米颗粒,所以每个金颗粒尺度约25～30 nm,金原子半径为0.144 nm(直径～0.3 nm),所以每个孤立金纳米颗粒包含三十余个金原子,因此并不是真正的单原子、单分子结构。然而,对大的分子结构,如若丹明、吡啶或单股核糖核酸的尺度>1.6m,而激光聚焦光斑φ～2m,这就可以说是单分子的行为了。

图4中给出的刀刃酵、酶在金或银胶态溶液蒸汽作用下,得到了附着在胶态团簇上的单股核糖核酸(DNA),左上角给出的四条拉曼谱线中的A、C、G和T分别是该结构中的腺嘌呤、胞嘧啶、鸟尿环和胸腺碱的特征峰。显然,这是单分子的增强作用才能显现出平常拉曼谱无法得到的信息。

Fig.3 Graphic of a typical single-molecule SERS experiment(left)；isolated gold nanoparticles and gold aggregates(right down)[9]

Fig.4 Graphic of DNA sequencing based on the intrinsic Raman spectra of the four bases.A,C,G and T are four feature peaks of DNA,in the left up insets[9]

3.3 斯托克斯和反斯托克斯

图5是银纳米团簇的等离激元(plasmon)共振曲线。它展示了不同激光线波长相对应的拉曼信号区域(A,B,C,D和E五个区域)。 A:1064 nm激发线的反斯托克斯区域；B,C∶830 nm激发线的斯托克斯区域和反斯托克斯区域；D:1064 nm激发线的超拉曼散射区；E:514.5 nm激发线的斯托克斯区域；图中谱线是银凝胶团簇光吸收随波长增大的衰减,过程中有各种不同拉曼散射信号。用近红外830 nm激发斯托克斯和反斯托克斯(B,C区)经历了同样的电-磁增强(谱线对称)。然而,用低于700 nm的514.5 nm激光激发的斯托克斯和反斯托克斯,经历了不对称的电-磁增强(谱线不对称)。

Fig.5 There is the Plasmon resonance curve of Ag-nanoclusters,notabene,the ordinate is absorbence[10]

图6是孤立金纳米颗粒的斯、反斯托克斯拉曼谱(a,b )；小聚集金球的斯、反斯托克斯拉曼谱(c,d)。增强了103～104,强度比有大的差异,(b)中较高频段热布居数较低,反斯托克斯谱较高频域缺失一些模式,这是因为热布居数较低所致,改用830 nm 近红外光激发,缺失的模式就得以显现(谱线d),强的反斯托克斯信号也在谱中给出,特别是在较高频区。反斯托克斯/斯托克斯的比值对于不同峰位(线)也不一样。

Fig.6 SERS Stokes and anti-Stokes Raman spectra for isolated gold nanoparticles (a and b),and on aggregates formed by these spheres(c and d)[11]

图7的左上方插图为胶体金团簇的表面增强拉曼谱。A,B 和C三点的激光功率密度分别为：3 mW/cm2、1.4 mW/cm2和0.7 mW/cm2；归一化拉曼信号随所用激光能量的增加而变大。反斯托克斯散射强度非线性的增加,而且比线性增长斯托克斯信号快。这源于分子或电荷转移共振效应,对斯托克斯和反斯托克斯散射特别的灵敏、有效。然而由于斯托克斯信号中未能满足弱饱和条件,就没有观测到二次方关系。

Fig.7 Raman scattering,Stokes and anti-Stokes in enhancement vs excitation intensity[12]

为了实验上的观察,散射截面和振动寿命的乘积必须为10-27cm2s,而振动寿命为10 ps,估算表面增强截面至少为10-27cm2s/10 ps～σ =10-16cm2,与正常的拉曼散射截面10-30cm2相比,相应SERS增强因子在1014量级；人们对150 nm及更大的分形银纳米结构,测出斯托克斯与反斯托克斯强度比,估推其增强因子亦在1014量级范围[11]。

3.4 斯托克斯和反斯托克斯的物理过程

Fig.8 Stokes and anti-Stokes scattering,there are three levels,double photons and one elementary excitations,may be called three、two and one,i.e.,(3、2、1)

图8中的拉曼斯托克斯-反斯托克斯跃迁过程中第一激发态N1粒子数变化可用变化率方程描述为：

(9)

式中,N0为基态元激发数,如分子等；N1第一振动受激元激发数,如分子等；σSERS为增强拉曼有效散射截面；nL为激光光子流密度；τ1为第一受激振动元激发寿命。再由变化率方程可推导出斯、反斯托克斯过程的布居方程分别为：

(10)

(11)

以上两布居方程满足的条件为：(1)稳态；(2)弱饱和,即满足如下不等式：

弱饱和：连续激光激发的拉曼布居与第一激发振动态布居可相比拟,或高于玻尔兹曼布居；但仍处于远离两能态(基态与第一振动态)中间的布居态。(11)式中的第一项是受激振动态热布居的反斯托克斯信息,第二项是强斯托克斯过程抽运作用,正常拉曼散射与热布居作用相比它可略去。因正常拉曼散射截面与寿命乘积为：σRS(ωm)·τ1(ωm)～10-40cm2·s。

也就是说大约需要1039/cm2s的激光光子(约1020W/cm2的激发强度)才能使拉曼抽运到与第一振动能级热布居相匹配的能级,即大约需要每平方厘米·每秒1039个激光光子(约每平方厘米1020瓦的激发强度)才能形成(抽运到)与第一振动能级热布居数相匹配的能级状态。

(12)

而

(13)

4 单分子SERS,纳米透镜、和热点(位等)

正如3.2节所说,对单分子,因其结构相差太大,单分子的增强有很大的不确定性和差异,现用纳米透镜(nanolens)作为特例讲解其物理含意及增强的过程。

4.1 纳米透镜(nanolens)

考虑由三个银纳米球组成的纳米透镜(图9),它给出了三个球的投影截面,三球的半径R(1,2,3) 分别为45、15和5 nm,每两球间距分别为d12=4.5 cm和d23=1.5 cm。

Fig.9 The nanolens is constructed by three silver nanospheres,their geometry parameters have been given in the statement[13]

自相似传输激发空间区域是完全可控重复出现的,图9可作为三个银纳米球的线性聚合,设其半径逐次减小的因子为1/3,该因子必须小于1,究竟是何值并不重要,但最大纳米球半径一定要小于入射波长,最小的半径要大于连续电动力学可适用的范围,即lce-m

随机系统的自相似性导致局域光场的巨大起伏。系统的尺度比波长λ小,等离激元的本征频率不取决于其大小,而是它的结构因子。考虑分形系统的最小尺度在自相似范围内,所以等离激元本征模被限制在最大的区域。本征模将与外来的辐射形成共振,进而产生增强的局域场,这些特性也延伸至最大范围。对于保持分形自相似性的较小的尺度区域,该局域场可看成是均匀的,增强的量值为Q,对小的自相似局域本征模,同样在Q-因子的基础上再增强Q-因子倍,也就是说,经过两次散射转换作用的总增强为Q2,不难看出,经过n次散射转换作用的总增强为Qn,随次数的增加该作用越来越弱。

纳米透镜中的(纳米)聚焦构成增强能力最强的区域,即最热的“热位”、“热点”或“增强元”。在最小的纳米球表面有最小的间隙(gap)。由|E|～1200 因子产生了局域场的增强为：

对于表面等离激元共振的真实情况,蓝光谱范围的Q约为10；纳米透镜的总增强为Q3,即1000倍。应该指出的是当纳米透镜的半经小于连续电动力学适用的范围时,增强作用的过程就停止了。考虑表面等离激元共振的光谱参数s(ω)约为1/3。显然,对于不同的纳米透镜有不同的光谱参数s(ω),即增强倍数亦不相同。

4.2 “热位”、“热点”、“增强元”或 “激活元”

“热位”(hot sites)、“热点”(hot spots) 、“增强元”(enhancement elements)或“激活元”(active elements)在增强中起了至关重有的作用,它们对总表面增强可分解为以下几个因素：

(1)g1是入射光在几个金属粒子的热位(点)等作用产生的增强；

(2)g2是聚集体所具有的特征；

(3)分子中几个靠近金属颗粒的局域拓扑性引发的增强g3。总增强可认为是以下三种增强的乘积：g =g1g2g3；g1是入射光在几个金属粒子的热位(点)等作用产生的增强；g2是源于组成热位(点)中分子与静止聚集体间的场散射；g3是组成热位(点)的局域拓扑贡献(107～109),g3≫g1g2,约为104。单分子表面增强还需要共振散射的贡献,才能达到1014～1015的增强因子,注意这仍只是推算得结果,并未真正测到。

用离散偶极子模型(DDA) 、时域有限差法(FDTD)对球、椭圆、棒、三角状、棱柱、立方、非球纳米颗粒结构作精确的理论计算,可得等离子体波共振频率和电磁场的空间分布和幅度[14]。遗憾的是这些内容仍未涉及增强和增强因子(EF)的内容。但已有人用以下的公式[15]：

和

可得到金纳米棒对D-核糖分子有较好的增强作用,增强因子EF约达5.6×105。

(4)增强因子的计算

电磁增强因子已能推算了,而所有增强作用的总增强因子可用实验测量方法计算出,即用增强后测得的强度与用正常办法测得的强度比值获得增强因子EF(enhancement factor)。

正常拉曼散射测得强度为:

若一切条件不变,仅换用具有增强作用的材料,则增强散射的强度再在上式中的强度表达式后,人为地添加增强因子EFSERS,即可写成：

这两式相比后,有：

这就是散射过程中所有增强的计算公式,但在实际应用时,确定参与散射的分子、原子或元激发数是有一定的困难,这可参见文献[15]121页给出的计算,进而得到相应的结果。

4.3 热位、热点等的物理实质

热位、热点(斑)等各种激活元都出现在纳米结构的交角、棱边、尖顶、边界、沟豁、槽穴等部位,它们都存在不同程度的微观作用的不确定性,即

能量与时间:ΔE·Δt～ћ

粒子数与相位:ΔN·Δφ～1

……

这就使得外来光波(电磁)场与结构中的某一特征量(如波矢、转动惯量、角动量和相位等中的一项)发生作用,使其中的某一物理量发生突变,相应共振条件得到满足时,就出现了“增强”。需补充说明的是,激光在各时空点上都有很好确定的相位。由此可精确的用于时空定位,时间定位的分辨间隔不超过一个周期；空间定位的分辨长度被限制在一个波长内。实际的精度取决相位确定的精度,对于可见光,波长在< 1m量级,周期为10-15s量级,这是可见激光测距时所能达到的精度。若用N表示凝聚在某一个单光子态中的光子数,通常是不确定的,起伏量为ΔN,若用φ 表示该系统中激光的相位,通常它也是不确定的,起伏量为Δφ,则粒子数和相位的不确定关系为：

ΔNΔφ～1

4.4 热点的实验研究

图10是浸泡在水中半径为20 nm 的银纳米颗粒的结构特性。每个热位含有颗粒数对五种不同的单光子激发随聚集体的增大而减少；在聚集体为10的颗粒附近有异常。

Fig.10 Number of hot spots vs.number of particles as a function of the size of the aggregate.Particles of Ag with radius equal to 20 nm and immersed in water have been considered[16]

图11表明每个颗粒含有热位数随聚集体的增大而减少；在五种不同的单光子激发聚集体为10颗粒附近有异常；不难看出：每个热位含有颗粒数远比每个颗粒含有热位数大,前者约为后者的百倍。

Fig.11 Mean number of particles per hot spot as a function of the size of the aggregate.Particles of Ag with radius equal to 20 nm and immersed in water have been considered[16]

5 其它“增强”

如前所述,光散射增强包含多种光与物质的作用过程中,逐步形成了“增强光谱学”,涉及的物质种类、实验方法、结果的解说等都大不同于早期的情况。

5.1 分形增强(波罗德定律)

早在上世纪50年代,G.波罗德等人就给出了小范围内两相介质的密度-密度相关函数γ(r) 的衰减的规律,从倒易空间可直接推导出波罗德定律[17]：由此可知该类结构界面引发的散射光强为：

(14)

该式中的R和a分别是“小范围”(凝胶聚集体、聚合物等)的尺度和“小范围”中包含每一个小组成单元(如原子,分子,纳米颗粒等)的大小,其波矢倒数就是它的尺度(图12)。

Fig.12 R,a=q-1are‘the small region’ and unit elementary,respectively e.g.,atoms,molecular,or nanometer particles[17]

(14)式中的d是单元的几何维数,DS是结构的分形系数,满足(d-1)≤DS≤d；若取d=3,则(14)式变为：

有

(15)

而R和a分别是图12中纳米颗粒的大小和组成纳米颗粒中散射元的大小,它们的量级分别是几到几十纳米和零点几个纳米。因此有：几倍≤I(q)≤105,即出现了增强。直到上世纪80年代之后,出现了纳米结构的新材料,才使该规律逐渐为人们所理解和采用,如银-钴合金在改变相对比份,即基质与掺入物的替换中出现的增强等现象[17]。

5.2 极性分子纳米结构的增强

(1)极性分子(如氟化锂等)纳米结构的复线性极化率为[17]:

(16)

(17)

(2)极性分子纳米结构的介电常数为[17]：

(18)

γ为阻尼系数;介电常数实部(ε′ ),虚部(ε″)分别为[17]:

(19)

(20)

因为ω≫ωt,从(18)和(19)两式可知：

ε′≈ε∞;ε″≈0

再由(17)式可得：GRS≫1,乃至于趋近∞,即出现了光散射增强。

5.3 相位增强

图13表示的倒波双向散射,在后向形成了多种散射的干涉：P-偏振,表面电磁波(表面等离激元-极化激元)；真空-金属界面及倒向偶极子,即粗糙表面同点等离激元-极化激元对与光的互作用。若入射波矢与散射波矢有相同的振幅和位相,部分波在反方向形成了逆向散射增强。须指出的是该过程中的数学公式都略去了。

Fig.13 Enhanced back light scattering of plasmon-polarition mechanism.The exciton of intermediate surface wave,i.e.,surface plasmon-polariton is essential for BLSE[18]

5.4 粗糙表面背散射增强

图14中的光正射于非常粗糙表面上,D是粗糙表面第一表面凸起与最后凸起间的距离。a是最大凸起与最邻近最小凸起的平均距离,近似等于高斯功率谱中横向相关长度。由于元激发配偶子(partner)的互相作用,出现背向光散射增强。

Fig.14 Enhanced back light scattering,the light incident normally on a very rough random surface[18]

Fig.15 The geometry configuration is same as in above Fig,but showing the partner wave scattered into a direction described by the scattering angleθs[18]

5.5 内外散射路径的相位增强

Fig.16 An illustration of two possible scattering paths that can lead to nonreciprocal effects[19]

(21)

5.6 准相位匹配增强

(22)

斯托克斯与反斯托克斯的动量守恒分别为：

(23)

式(22)和(23)能结合成自动相匹配、两步χ(2)过程。因而出现高阶散射增强,多达11级。拉曼谱呈现了多峰结构、(2n+1)个等间距频率、不连续梳状谱；在以样品为中心投影点散射光形成同心圆环(图18)。

Fig.17 Phase matching in the cascaded generation of anti-Stokes and Stokes Raman signals.Only the first three order are sketched for simplification[20]

Fig.18 Raman spectra with(a)ωp=19 cm-1;λ0=531.82 nm,(b)ωp=8.5 cm-1;λ0=531.92 nm.The insets are the corresponding spatial distribution for scattering light[20]

ω0= ωs(n)+ ωas(n)

式中的n=1,2,3…。显然,该情况的量子过程已不再是“3、2、1”所能描述得了,不再是一阶线性光散射的物理问题了。在非弹性光散射增强中,准相位匹配方法成功的被引入χ(2)介质中。比值Ias(n)/Ias(n-1)随级数n增加而变大,从14% (n=1) 增加到70%(n=8) 。反斯托克斯散射光强随级数增大而增强,这是典型的非线性增强特征。

6 光散射增强谱理论

下面从三方面讲述该问题：(1)局域场的谱展开和格林函数；(2)格林函数理论SERS 增强因子；(3)数值计算及其结果：(a)偶极近似分形SERS增强；(b)随机系统单分子SERS增强。

6.1 局域场谱的表示

考虑金属纳米系统嵌埋在介电基质体中,金属介电函数为εm(ω),它取决于光频率ω。介质的介电函数为εd,纳米系统的尺度l比入射光波波长λ小很多,即l≪λ,则准静态近似中的势φ(r)满足以下的连续方程：

(24)

空间介电函数变化的表示式为：

ε(r)=εm(ω)θ(r)+εd[1-θ(r)]

式中θ(r)是系统的特征函数,当r在金属内时为1,否则为 0。

考虑系统受具有φ0(r)势的外场在光频率ω激发,该势由外电荷产生,因此在该系统内满足拉普拉斯方程：

(25)

其场势为：φ(r)=φ0(r)+φ1(r)

而φ1(r)是系统四周表面S满足均匀狄义赫利-诺伊曼条件的局域场,可设：

(26)

n(r)表示在r垂直于表面S,这是确定本征模的充(分)(必)要条件。

同样,我们假设金属纳米系统完全被包在边界S内,且不与它有任意一点接触,因而出现以下的辅助边界条件：

只要我们选取适当的金属亚系统边界表面,上述辅助边界条件总能得到满足,再加上这三个方程可得到二阶椭圆方程(27)式,该方程的右边描述了外激发源：

(27)

这里,已引入光谱参数

6.2 格林函数

为了得到该方程的格林函数,引进下述方程

(28)

它的本征函数及本征值分别为φn(r)、sn,φn(r)满足(26)式给出的均匀狄义赫利-诺伊曼条件。重要的是该本征问题仅取决于系统的几何性质,而不取决于材料的组分。因此,对给定几何特性的系统,可解决所有频率和任意材料组份的光学响应。物理上的本征模式由表面等离激元方程确定,它的频率是复数ωn+iγn,它由复数方程

δ(r-r′)

(29)

确定s(ωn+iγn)=sn,对于弱弛豫,γn≪ωn,表面等离激元频率的实部满足以下的方程：

(30)

6.3 狄义赫利-诺伊曼边界条件

对于函数φ(x)：(1)在一个周期内,周期信号x(t)必须绝对可积；(2)在一个周期内,周期信号x(t)只能有有限个极大值和极小值；(3)在一个周期内,周期信号x(t)只能有有限个不连续。

边界含义,在物理上可有以下两种：(1)周期、平整层构成的(interfaces) (图1)；(2)任意曲面构成的(boundary)(图2)。

6.4 谱的“极”及其物理意义

表面等离激元谱宽为γn,表示为：

(31)

由克喇末-克朗尼格(Kramers-Kronig)色散关系引导出的金属介电函数不等式(组)为：

(32)

(33)

式中V是系统的体积。

上述过程中所有标积的充要性质都应该得到满足,即,(1)二进制,(2)哈密顿量自洽,(3)定义为正算符。由此可得到该标积的本征函数的正交归一化为：

(34)

所有的本征值sn是实的,而且所有的本征函数φn(r)可选择为实的,则1≥sn≥0。这些本征函数构成了满足边界条件的空间完整基矢,用表示。延迟格林函数r(r,r′;ω)满足以下的方程：

(35)

(36)

将它代入(35)式,乘φn(r)再对整个体积V积分,即可得an,则格林函数为：

(37)

准静态近似条件下,它是正确的,它包含了任何频率,各种激发光(场)下纳米体系线性响应的最大信息量。所有本征模式(表面等离子)的展开式都满足格林函数的一般性质。所有这样的模式都由相应格林函数的极(pole)来描述。“极”就是具有能量的(元激发)状态,谱的中心能级,等同于谱的某一峰。第n个“极”的频率和谱峰宽分别由sn和γn给出。

(38)

将格林函数写成临近“极”的渐近表示式：

(39)

对于频率接近第n个“极”的格林函数增强因子为：

(40)

这就是共振(表面-等离激元)的品质因子。为了估计它的量值,再次考量以下不等式中的介电函数

(41)

用金属的相对介电函数代换基底介质的介电函数,即εm→εm/εd,可得到：Qn≥Q(ωn),

(42)

对较低极限,品质因数仅是频率的函数,不取决于表面-等离激元本征函数。

对银和其它人工制备出来的金属,在可见光到近红外光谱范围内,Q(ω)≫1都成立。“谱”的格林函数方法另一非常重要的性质是系统几何性质与其材料性质完全无关,它的本征函数φn,本征值sn仅由系统的几何性质确定,完全独立于材料的组分和受激的频率。因此,一旦几何特性确定后,本征问题也就解得。若已知系统材料的介电常数,则其组分和受激频率都包含在格林函数的表示式中的参量(本征值)s(ω)中。一旦格林函数找到后,作为激发势φ0(r)的缩写局域光场势φ1(r)也就求得：

(43)

从(43)式和φ(r)=φ0(r)+φ1(r)两式,及辅助边界条件可得场势为：

φ(r)=

(44)

最后,微分该式,可得到光电场E(r)表示成激发(外)场E0(r)的封闭表示式：

(45)

式中的α,β,…是欧几里德矢量指标(α,β,…=x,y,z),求和遍及所有指标；这些场为：

(46)

并矢张量延迟格林函数定义为：

(47)

(48)

另外,考虑本征问题是实的且对称,它的本征值(sn)总是实的,本征函数φn也总能被选为实的。因此格林函数也满足较简单的微扰对称,即

(49)

若激发源是光波,在纳米系统中的波前是平的,即E(0)为常数,由此可得：

(50)

局域场增强因子是由压缩延迟并矢格林函数组成：

(51)

6.5 格林函数理论中的增强因子

拉曼散射是非相干过程,用(电)极化(强度)PR(r)描述它。这相当于用拉曼频率ωR,拉曼场势φR(r)的准静态方程来描述,因而有以下的方程：

(52)

它的积分解为：

(53)

假设PR(r′)在边界 S 消失(这与边界条件自洽),则由高斯理论(部分积分),可得拉曼频率光电场矢量的格林函数表示式：

(54)

PR(r)=δ(r-r0)dR(r0)

(55)

式中dR(r0)为拉曼过渡偶极子,以频率ωR振荡,结合到(54)式,作用在金属上电场为：

(56)

该电场作用在金属组分后的介电磁极化率为：

(57)

则感应的总拉曼偶极矩为：

(58)

因子θ(r)限制了积分体积仅在金属内。由格林函数的对称性可得总拉曼辐射偶极矩：

(59)

(59)式中方括号第一项是被局域光场感应的拉曼偶极子,第二项描述了整个纳米结构的天线效应,该结构被重整化,增强属拉曼偶极子辐射。拉曼偶极子dR正比于局域场E(r0),由此出现了拉曼极化率αR(ω),为了简化,仅考虑为各向同性(标量)激发场,则总拉曼辐射偶极子为：

(60)

显然,可以假设激发场E(0)是线性Z-偏振、则沿Z轴不求和,增强因子为：

(61)

式中gβ z(r0,ω)表示局域场的增强,而

gβ z(r0,ωR)/s(ωR)

(62)

是纳米结构由于天线效引发拉曼偶极子增强,(61)式可简化为：

gR=

(63)

由(63)式可估算增强因子；进一步的简化后可得：

(64)

不难看出,总增强由两部分组成(并不是如前所述的三部分),即,(1)局域场感应的拉曼极化；(2)金属纳米结构共振天线效应。注意这里并没有给出“拓扑”增强的贡献；即使如此,增强因子仍很难求出。迄今,仍未能用该公式直接计算出增强因子。

7 讨论与结论

所有金属中品质因子最好的是银(Ag),在10(可见光)～100(近红外光)范围,由此可估算单分子银的增强因子最高可达gR～(100)4=108。但离1014～1015,相差还有百万量级以上,说明增强(因子)的研究还有很大的未知不确定性。

如果考虑格林函数中分子的本征函数情况又将有何变化,研究的问题又将做何改变；如不是金属纳米系统,而是任何物质组成的纳米系统,情况将又该是怎样？这些都是有待考查研究的问题。

7.1 困惑

对2000年8月20日-8月25日北京召开的17届国际拉曼光谱会议的大会特邀报告中[1]的内容,原文都没有给出直接测到的结果,目前的光谱仪也不可能直接测到如此高的增强(1014～1015)。

该文中写到：“The observed enhancement factors are on the order of 1014to1015”,“观察、观测,监视……看到”是“observed”的词意,试问何种测量手段、仪器、方法等能测出如此高数量的增强因子,百万亿倍～千万亿倍的增强,这是何等高的增强！

图19谱线中9#应该是没有信息的,而其余的1-8#都出现不同谱峰,意即：从零峰增至有峰,从0→1,即这时的增强为∞,所以,百万亿倍到千万亿倍的增强,当然是可以的,但决不是“observed”的结果(论)。笔者已仔细(查)阅读过相关的经典原文,均未发现如此超高的增强因子是如何“观察”、“观测”、“监视”……“看到”的说词。

Fig.19 Raman spectra of a single R6G molecule recorded at 1-s intervals.Raman signals abruptly changed for 9#→8# spectral lines[1,21]

7.2 结论

(1)不要仅强调表面增强,因各种材料表面尺度相差甚远；对非表面结构出现的增强,如：准相位,逆向反射,等离激元-极化激元干涉等光散射增强现象不一定都发生在表面结构。

(2)特高的“增强因子”并未真正测到,只是与散射截面数量级的比较、推理中得到的。

(3)格林函数对增强因子计算还未显现其积极作用。

(4)除拉曼散射中存有“增强”外,还有其它光与物质作用的光散射中有该现象,因而应该说成“光散射增强”。准确的说,“增强因子”不仅与物质类别有关,更取决于参与该过程的元激发数。

7.3 后记

正如过往指出过的[22],知识的长河蜿蜒流逝,舍取或长存的仅是人们自身择弃吗？不,还应有时间的考验；时间的考验既是真实严肃的,更是可靠的！亦如T.A.爱迪生曾告诫,世上最艰巨的使命是什么？是思考。如何去思考？某世界著名实验室的过道上就有“Big Thinking”的警醒语；按中文的字意,是否可理解为：多思、深思、善思、勤思、广思、寻思等意义。对自然科学(物理、化学、材料、生物、医药、地质、地理、天文、气象等)的探究,要靠从事该项工作的人们不断探究其规律、特质,终其一生。

真如千百年前,我国伟大诗人杜甫所献箴言：

“细推物理须行乐,何用浮名绊此身。”

显然,其中的“物理”,不是当下所说的物理专业所含盖的内容。此外,“绊”字若改为“伴”、“拌”或“扮”三字,又将是何种意义,不再赘述。从事科研和教学的人们一定都知道,贯其终身的教学和科研工作分别是：

“教学”—系统、概括的,顺理成章的讲述；是有依据的重复；常与循规蹈矩结缘。表现为：思索呀！哲理无穷,但总还能够思索！

“科研”—理性思维的奔放和不羁,潜在的困惑,无太多依据的探奇求鲜。常是顿悟的前提,与思绪的颠沛沉重结缘,表现为：奋进吧！道路坎坷,但必须前进！

致谢

感谢该实验室对本工作的支持及001CB61404课题组的资助。感谢南京大学秦国毅教授在“格林函数”中的有益讨论。

本文部分内容在2015年10月22日-10月25日,四川大学召开第18届全国光散射学术会议物理与材料分会场邀请报告中给出。

[1] Shuming Nie,Steven R Emory.Surface-enhanced Raman scattering of single molecules and single nanoparticles:Proceedings of XVIIth International Conference on Raman Spctroscopy[C].Zhang Shulin,Zhu Bangfen.John Wiley &Sons,LTD,2000:20.

[2] Fleischmann M,Hendra P J,Mcquillan A J.Raman spectra of pyridine adsorbed at a silver electrode[J].Chem Phys Lett,1974,26(2):163-166.

[3] Jeanmarire D L,Van Duyne P R.Suface Raman spectra electrochemistry part I.Herterocyclie aromatic and aliphatic amaines,adsorged on the anodized silver electrode[J].J Electroanal Chem,1977,84(1):1-20.

[4] Albrecht M G,Creighton J A,Anomalously intense Raman spectra of pyridine at a silver electrode[J].J Am Chem Soc,1977,99(15):5215-5219.

[5] Otto A.Surface-enhanced Raman scattering:“classical” and “chemical” origins [M].Cardona M,Gǖntherodt G(ed.),Light Scattering in Solids IV,1984,54:289-418.

[6] Kneipp K,Kneipp H,Moskovits M,etal.Surface-enhanced Raman scattering,physics and applications [M].Springer,2006.

[7] Winfried Mönch.Semiconductor surfaces and interfaces[M].Springer,2001:290.

[8] Cheng Guangxu.Nanostructural and thin film materials studies by Raman and Brillouin scattering [J].The Journal of Light Scattering,2010,22(3):196-206.

[9] Kneipp K,Kneipp H,ItzkanI,etal.Surface-enhanced Raman scattering and biophysics[J].J Phys:Comdens Matter,2002,14(18):R597-R624.

[10] Kneipp K,Kneipp H.SERS signals at the antistokes side of the excitation laser in extremely high local fields of silver and gold nanolusters[J].Faraday Discuss,2006,132:27-33.

[11] Kneipp K D,Kneipp H,Manoharan R,etal.Extremely large enhancement factors in surface-enhanced Raman scattering for molecules on colloidal gold clusters [J].Appl Spectrosc,1998,52:1493-1497.

[12] Kneipp K D,Kneipp H,Itzkan I,etal.Near-infrared surface-enhanced Raman spectroscopy of biomedically relevant single molecules on colloidal silver and gold clusters[M].Photonics West-BIOS 2000(SPIE,SanJose,CA),49.

[13] Li K,Stockman M I,Bergman D J.Self-similar chain of metal nanospheresas an efficient nanolens[J].Phys Rev Lett,2003,91:227402-4.

[14] 莫冰,李和平,陈娟,等.表面增强拉曼光谱及其在定量测量中的研究进展[J].光散射学报,2013,25(3):219-234.(Mo Bing,Li Heping,Chen Juan,etal.Surface enhanced Raman spectroscopy and its progress in quantitative detection[J].The Journal of Light Scattering,2013,25(3):219-234)

[15] 农凯,刘仁明,司民真.D-核糖NIR-SERS光谱及其在金纳米棒表面吸附行为分析[J].光散射学报,2014,26(2) 117-123.(NIR-SERS and adsorption behavior studies of D-ribose on the surface of the Au nanorods[J].The Journal of Light Scattering,2014,26(2):117-123.

[16] Corni S,Tomasi J.Studying SERS from Metal Nanoparticles and Nanoparticles Aggregates with Continuum models[M].//Kneipp K,Moskovits M,Kneipp H.Surface-Enhanced Raman Scattering Physics and Applications[M].Topics Appl Phys,2006,103:105-123.

[17] 程光煦.拉曼 布里渊散射:第二版[M].北京,科学出版社,2007:289,309-313,326.

[18] Wolf E.Progress in optics[M].Elsevier,2004:133.

[19] Maradudin A A,Méndez E R.Scattering by surfaces and phase screen:Scattering [G].Elsevier,2002:864-894.

[20] Xu P,Zhu S N,Yu X Q,etal.Experimental studies of enhanced Raman scattering from a hexagonally poled[J].Phys Rev B,2005,72:064307-5.

[21] Nie S M,Emory S R.Probing single molecules and single nanoparticles by surface-enhanced[J].Science,1997,275:1102-1106.

[22] 程光煦,张杏奎,顾刚,等.全碳分子及其掺杂体结构的喇曼研究[J].物理学进展,1995,15(3):286-306(Cheng Guangxu,Zhang Xingkui,Gu Gang,etal.Investigations of structures for all-carbon molecules and doped solid thin films byRaman spectroscopy[J].Progress in Physics,1995,15(3):286-306)

Also Talking about the Enhanced in Light Scattering

CHENG Guang-xu

(NationalLaboratoryofSolidStateMicrostructuresandPhysicsDepartment,NanjingUniversity,Nanjing210093,China)

‘Enhancement phenomena’ in light scattering were found at 1970s.It is an importance phenomenon for (especial inelastic) light scattering.Up to now,it had been expended a huge effort and funds in this phenomena studies,or for more best explain away these results during the past more ten years.Recently,it had been pushed on the new place by super-high enhancement(gis the enhanced factor ～1014-15)phenomena,and for this sort of problems,experimental results,must deal with by using new idea or scattering crosses section.There are details given a few of machines about facility-pole of Green’s function,polarization,nanoparticles,nanolens,quasiphase-matching,single-molecule and interface layer or the boundary etc.,which are unable understanding during the past a few decade.Except fundamental knowledges of light scattering intensity have been presented,for the new fields should been given too,for their research in further,in this talking.

(inelastic) light scattering;enhancement

2015-12-16; 修改稿日期:2016-03-12

程光煦(1943-)男,教授,长期从事光散射(拉曼 布里渊)物理和光谱物理的科研、教学工作。E-mails: gxcheng@nju.edu.cn

1004-5929(2016)04-0374-17

O436

A

10.13883/j.issn1004-5929.201604016