不同汇合方式自捻纱的捻度分布

崔 红， 高秀丽， 高大伟， 张 伟

(1.盐城工学院 纺织服装学院，江苏 盐城 224000； 2.河南工程学院 纺织学院，河南 郑州 450007)

不同汇合方式自捻纱的捻度分布

崔 红1， 高秀丽2， 高大伟1， 张 伟1

(1.盐城工学院 纺织服装学院，江苏 盐城 224000； 2.河南工程学院 纺织学院，河南 郑州 450007)

通过构造自捻纺纱过程中两根单纱条从自捻罗拉钳口线输出后至汇合点的捻度分布函数，推导出不同汇合方式自捻纱线的捻度分布函数，由自捻纱线的捻度分布函数得出实际纺纱条件下不同汇合方式在半周期长度上的自捻捻度分布图像.该图像表明，有相位差的汇合方式自捻捻度分布峰值低于同相自捻纱.对不同汇合方式进行实际纺纱实验，对纱线特征及性能的测试结果表明，不同的汇合方式改变了自捻纱线的相位差，相位差的存在尽管使自捻捻度分布函数峰值降低，但同时减少了自捻纱线上弱捻区域的长度，使纱线的强伸性能得以提高.

单纱条；自捻纱；不同汇合方式；捻度分布函数；同相；相位差

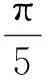
1 3种汇合方式的捻度分布函数

图1给出了3种不同汇合方式的自捻纺纱过程.纱1：汇合方式1(同相纱)；纱2：汇合方式2(相位纱1)；

D—自捻罗拉往复动程；P—单纱条的周长；L1—主牵伸区前罗拉钳口线与自捻罗拉钳口线之间距离；L2—自捻罗拉钳口线与汇合钩之间距离；L3—汇合钩C3与导纱钩D3之间的垂直距离(第3种汇合方式)；O1—纱条A1和纱条B1的汇合点; O2—纱条A2和纱条B2的汇合点;O3—纱条A3和纱条B3的汇合点; e—两根单纱条间距；X—加捻周期长度；Z—输出纱条长度；T1(Z)—L1段纱条上的捻度分布函数；T2(Z)—L2段纱条上的捻度分布函数；A1，B1，T2A1(Z)，T2B1(Z)—纱条A1和B1在L2段上的捻度分布函数；A2，B2，T2A2(Z)，T2B2(Z)—纱条A2和B2在L2段上的捻度分布函数；A3，B3，T2A3(Z)，T2B3(Z)—纱条A3和B3在L2段上的捻度分布函数；t1，t2，t3，Tst1(Z)，Tst2(Z)，Tst3(Z)—3种汇合方式自捻纱的捻度分布函数.图1 自捻纺纱3种不同汇合方式示意Fig.1 A schematic diagram of three convergence modes in self-twist yarn

纱3：汇合方式3(相位纱2).这3种汇合方式所得的3种纱线分别用纱1、纱2、纱3来表示.纱1为同相纱，纱2和纱3为相位纱.自捻纺纱主牵伸区前罗拉与自捻罗拉之间L1段上的捻度分布函数T1(Z)和自捻罗拉与汇合钩之间L2段上的捻度分布函数T2(Z)见1.1和1.2.

1.1 理想状态下L1段纱条上的捻度分布函数[6-8]

理想状态就意味着纤维条的加捻函数为正弦函数，加捻效率恒为1,

(1)

1.2 理想状态下L2段纱条上的捻度分布函数

(2)

(1) 纱1中A1纱条和B1纱条在L2段上的捻度分布函数为

(3)

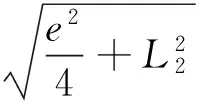
(2)纱2中A2纱条在L2段上的捻度分布函数为

(4)

纱2中B2纱条在L2段上的捻度分布函数为

(5)

(3)纱3中A3纱条在L2段上的捻度分布函数为

(6)

纱3中B3纱条在L2段上的捻度分布函数为

(7)

1.3 3种汇合方式的自捻捻度分布函数

对于自捻捻度和两根单纱条捻度之间的关系，国内外学者根据自捻捻度的力学结构和几何特征，求得了两者之间的理论公式,如澳大利亚学者Henshaw[9]建立了公式(a1)：

(a1)

我国学者王兟[10]建立了公式(a2)：

(a2)

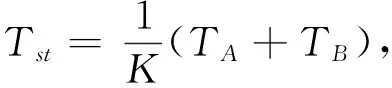
由以上各纱条的捻度分布函数可得到3种不同汇合方式的自捻捻度分布函数如下：

纱1的自捻捻度分布函数为

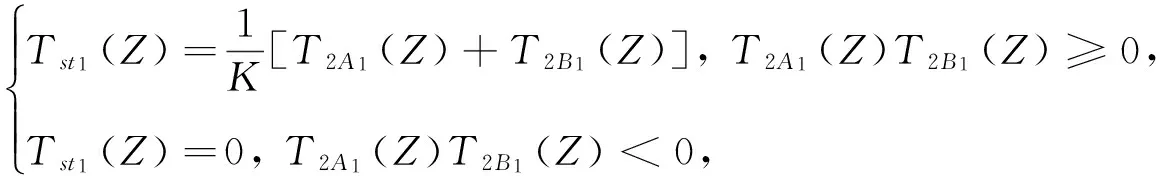
纱2的自捻捻度分布函数为

纱3的自捻捻度分布函数为

将以上捻度分布函数分别代入得到3种不同汇合方式的自捻捻度分布函数表达式.

由式(3)得纱1的自捻捻度分布函数：

(8)

由式(4)和式(5)得纱2的自捻捻度分布函数：

(9)

由式(6)和式(7)得纱3的自捻捻度分布函数：

(10)

2 3种汇合方式的捻度分布

根据式(8)、(9)、(10)得出的3种不同汇合方式自捻捻度分布函数，利用已知纺纱参数代入，如L1=45 mm，L2=15 mm，p=0.885 7 mm，X=210 mm，D=76 mm，e=19 mm，L3=17 mm，得出3种不同汇合方式的自捻捻度分布函数：

将以上3种情况下的自捻捻度分布函数用Matlab编程，得到图2.

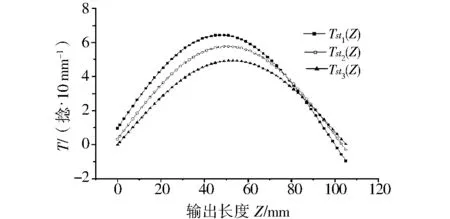
图2 不同汇合方式半周期长度上自捻捻度分布Fig.2 Twist distribution of different convergence modes on half cycle

由图2可以看出，3种不同汇合方式中，纱1的自捻捻度峰值最高，纱2和纱3的自捻捻度峰值均低于纱1，纱3的峰值最低.造成这种结果的原因在于同相自捻纱纱1的两根纱条从自捻罗拉输出至汇合钩处汇合时，由于两根纱条从自捻罗拉钳口至汇合钩的长度相等，故两根纱条的有捻区和无捻区两两相对，两根有捻区的纱条在汇合时由于两根单纱条圆周向相互约束，两根单纱条同时退捻产生自捻.无捻区的两根纱条由于没有圆周向约束而呈现无捻的状态，是纱条上强力最弱的区域.由于相位差的存在,纱2和纱3的有捻区和无捻区错开一定的距离，一根纱条的有捻区往往和另一根纱条的部分有捻区和无捻区相遇，这时由单根纱条退捻所获得的自捻捻回数减少，纱条上弱捻区的长度也同时减少.

3 3种不同汇合方式纺纱实验

用3种不同汇合方式进行实际纺纱，分别纺制98.8 tex和226.0 tex两种自捻纱线,得到纱线的S捻捻回数、S捻段长度、Z捻捻回数、Z捻段长度及相邻无捻区长度、断裂强力等指标见表1.

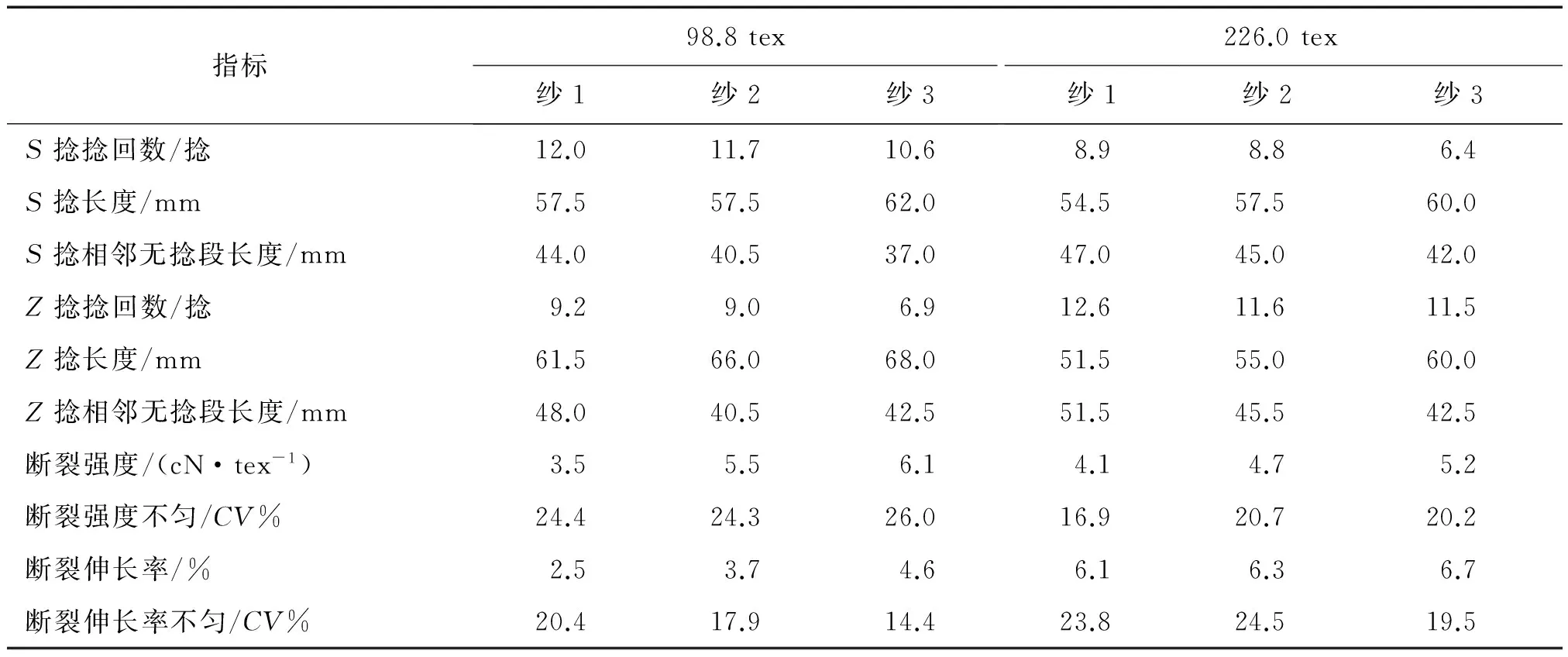
表1 3种不同汇合方式纺纱实验结果Tab.1 Yarn properties of three convergence modes

从表1可以看出，相同特数的纱1与纱2、纱3相比，纱2和纱3的S捻捻回数和Z捻捻回数比纱1少，这是由于相位差使一根纱条的无捻段镶嵌在另一根纱条的有捻段当中，自捻纱线自捻的形成仅靠单根纱条的退捻力矩来完成，使自捻捻回数减少，这与图3中自捻捻度的分布规律吻合.而纱2和纱3自捻纱线的S捻长度、Z捻长度、断裂强度、断裂伸长等指标比纱1均有所增加， S捻和Z捻段相邻的无捻区长度减少.其中，S捻长度、Z捻长度的增加和S捻段、Z捻段相邻无捻区长度的减少是由相位差造成的.因为无捻区长度是决定自捻纱线拉伸性能的主要区段，所以其长度减少是造成自捻纱线断裂强度和断裂伸长率增加的主要原因.98.8 tex纱2和纱3的断裂强度与纱1相比分别增加了57%和74%，其断裂伸长率与纱1相比分别增加了48%和84%，大大提高了自捻纱的强伸性能.

4 结语

以牵伸区前罗拉钳口线至自捻罗拉钳口线之间的一段纱条L1上的捻度分布函数和自捻罗拉钳口线至汇合点O之间的一段纱条L2上的捻度分布函数为基础，得到了不同汇合方式下两根单纱条的捻度分布函数，从而推导出不同汇合方式下自捻纱线的捻度分布函数.并且,由两根单纱条的捻度分布函数得出了实际纺纱参数条件下不同汇合方式在半周期长度上自捻捻度的分布图像，该图像表明，有相位差的汇合方式自捻捻度分布峰值低于同相自捻纱.对不同汇合方式进行实际纺纱实验，对纱线特征与性能的测试结果表明,不同的汇合方式改变了自捻纱线的相位差，相位差的存在尽管使自捻捻度分布函数的峰值降低，但同时也减少了自捻纱线上弱捻区域的长度，从而使纱线的强伸性能得以提高.

[1] HENSHAW D E.Self-twist Yarn[M].Watford:Merrow Publishing Company Limited,1971.

[2] 姚瑞源，蒋金仙.自捻纺纱[M].北京：纺织工业出版社，1985：38-45.

[3] ELLIS B C，WALLS G W.STT yarns:technological aspects of twisted self-twist yarns[J].Journal of the Textile Institute，1970，61(6)：279-303.

[4] ELLIS B C，WALLS G W.Towards the better understanding of self-twist structures[J].Journal of the Textile Institute， 1973(64)：386-389.

[5] 崔红，肖志永，郁崇文.自捻纱的捻度分布特征分析[J].纺织学报，2012,33(8):40-45.

[6] WALLS G W.Oscillating rollers for self-twist spinning[J].Journal of the Textile Institute，1970,61(6):245-259.

[7] HENSHAW D E.Twist distribution in self-twist yarn[J].Journal of the Textile Institute，1970,61(6)：269-278.

[8] 王兟，张知佑.自捻捻度分布的测定与统计分析[J].棉纺织技术,1985,8(1):22-26.

[9] HENSHAW D E.A model for self-twist yarn[J].Journal of the Textile Institute,1970,61(3):97-107.

[10]王兟，张知佑.自捻捻度与纤维条捻度之间理论关系的论证[J].纺织学报,1987,8(11):691-694.

Study of twist distribution functions on different self-twist yarn convergence modes

CUI Hong1, GAO Xiuli2, GAO Dawei1, ZHANG Wei1

(1.CollegeofTextilesandClothing,YanchengInstituteofTechnology,Yancheng224000,China;2.CollegeofTextiles,HenanUniversityofEngineering,Zhengzhou450007,China)

Twist distribution functions of self-twist yarn are examined by calculating the twist distribution functions of two strands from the nip of self-twist rollers to the convergence point in three different convergence modes. Twist distribution images of three different convergence modes on half cycle length are presented by the twist distribution functions. The images show that the self-twist yarn with phase difference has a lower self-twist peak than in-phase self-twist yarn. Test results from the actual spinning different convergence modes for self-twist yarns show that different convergence modes changed the phase differences so that make the yarn properties improved.

strand; self-twist; different convergence mode; twist distribution function; in-phase; phase difference

2015-09-29

江苏省高校自然科学基金面上项目(15KJB430032)；盐城工学院人才引进项目(KJC2014012)；盐城市2014年度农业科技指导性计划项目(YKN2014017)

崔红(1972-)，女，河北沧州人，高级工程师，博士，主要研究方向为纺纱工艺原理.

TS134.7

A

1674-330X(2016)02-0001-05