线性差分方程亚纯解的若干性质

杜云飞, 赵 明

(北京航空航天大学 数学与系统科学学院,北京 100191)

线性差分方程亚纯解的若干性质

杜云飞, 赵 明

(北京航空航天大学 数学与系统科学学院,北京 100191)

研究了多项式系数差分方程Pn(z)f(z+n)+…+P1(z)f(z+1)+P0(z)f(z)=0和Pn(z)f(z+n)+…+P1(z)f(z+1)+P0(z)f(z)=F(z)的亚纯解的增长性、零点收敛指数和小函数之间的关系, 得到的结果推广了相关的结论.

差分方程；亚纯解；小函数

复差分方程是复分析领域一个重要的研究方向.Nevanlinna值分布理论引入以来,复域差分和差分方程逐渐成为一个热门的研究课题,尤其是线性差分方程,有许多学者对其解的有关性质做了大量研究.本研究在Chiang和Feng的定理A与Chen和Shon的定理C和定理D的基础上,进一步研究了相关差分方程解的增长级和零点收敛指数等性质,对有关结果做了进一步推广.

1 背景及主要结果

采用亚纯函数Nevanlinna理论的基本概念和符号[1-3],其中σ(f)表示亚纯函数f(z)的增长级,λ(f)表示f(z)的零点收敛指数,τ(f)表示f(z)的不动点收敛指数,定义如下：

用S(r， f)表示在除去一个有限线性(对数)测度集合外满足r→∞时,S(r， f)=o(T(r， f))的量,一个亚纯函数α(z)如果满足T(r，α)=S(r， f)，则称其为关于f(z)的小函数.用λ(f(z)-α(z))表示f(z)-a(z)的零点收敛指数,定义如下：

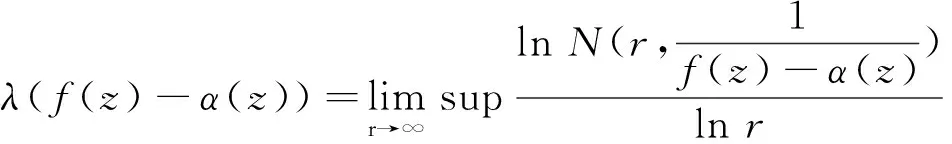
近年来,出现了大量研究复差分及复差分方程的文章,如文献[4-9].Chiang和Feng[10]对线性差分方程进行了研究并且获得了下面的结果.

定理A 设P0(z)，…，Pn(z)是多项式且存在整数0≤l≤n，使下列条件成立：

(1)

若函数f(z)是方程

Pn(z)y(z+n)+…+P1(z)y(z+1)+P0(z)y(z)=0

(2)

的亚纯解,则其增长级满足σ(f)≥1.

Ishizaki 和Yanagihara研究了如下形式差分方程的超越整数解的增长性:

Qn(z)Δnf(z)+…+Q1(z)Δf(z)+Q0(z)f(z)=0，

(3)

式中:Qn(z)，…，Q0(z)是多项式, Δf(z)=f(z+1)-f(z), Δnf(z)=Δ(Δn-1f(z)), 获得了下面的定理B.

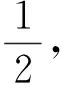
ln M(r，f)=Lrx(1+o(1)),

式中:有理数x是牛顿多边形方程(3)的斜率,L>0是常数,特别地有x>0.

对比定理A和定理B,可以看出方程(3)可以写成方程(2)的形式, 但是定理A在条件(1)下确保了方程(2)的所有解满足σ(f)≥1.而在定理B的条件下,方程(2)可能存在超越亚纯解f(Z),满足σ(f)<1.

Chen[11-12]弱化了定理A中的条件(1)并且得到了下面的结果：

定理C 设P0(z)，…，Pn(z)是多项式且满足PnP0≢0及

deg(Pn+…+P0)=max{deg Pj∶j=0，1，…，n}≥1,

(4)

那么对于方程(2)的任意有限级亚纯解f(z)(0)满足σ(f)≥1， f(z)取值每一个非零值a∈C无穷多次且有λ(f-α)=σ(f).

定理D 设如下方程的系数F(z)，P0(z)，…，Pn(z)是多项式且满足FPnP0≢0及

Pn(z)y(z+n)+…+P1(z)y(z+1)+P0(z)y(z)=F(z)，

(5)

那么对于方程(5)的任意有限级亚纯解f(z)满足σ(f)≥1且有λ(f)=σ(f).

在上面结论的基础上近一步研究并对上述结果进行改进和推广,得到以下主要结论：

定理1.1 设P0(z),…,Pn(z)是多项式满足PnP0≢0及deg(Pn+…+P0)=max{deg Pj∶j=0，1，…，n}≥1.

α(z)是σ(α)<1的非零亚纯函数, 那么对于方程(2)的任意有限级亚纯解f(z)(0)取值a(z)无穷多次且有λ(f(z)-α(z))=σ(f(z))≥1.

定理1.2 设F(z),P0(z),…,Pn(z)是多项式且FPnP0≢0, α(z)是σ(α)<1的超越亚纯函数,那么对于方程(5)的任意有限级亚纯解f(z)可以取值α(z)无穷多次且有λ(f(z)-a(z))=λ(f(z))=σ(f(z))≥1.

特别地,在定理1.1中，如果a(z)≡z或者a(z)≡a(∈C{0}),可以得到推论1.1和推论1.2.

推论1.1 设方程(2)中系数P0(z),…,Pn(z)是多项式满足PnP0≢0及条件(4),那么对于方程(2)的任意有限级亚纯解f(z)(0)满足τ(f)=σ≥1.

推论1.2 设方程(2)中系数P0(z),…,Pn(z)是多项式且满足PnP0≢0及条件(4), 那么对于方程(2)的任意有限级亚纯解f(z)(0)满足σ(f)≥1,进一步地， f(z)可以取每一个非零值a∈C无穷多次且有λ(f-a)=σ(f).

1.1推论1.2即定理C .

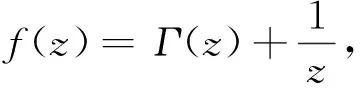
2 引理

引理2.1 设g(z)是复平面上σ(g(z))<1的超越亚纯函数,h>0,则存在一个ε-集合E满足当z→∞(z∈CE)时对于|c|≤h,一致地有

更进一步,集合E可以有选择地使充分大的z∉E满足g(z)在|ζ-z|≤h中无零点和极点.

引理2.2 设ω是差分方程P(z,ω)=0的超越亚纯解,其增长级为σ(<∞),其中P(z,ω)是关于ω(z)及其位移的差分多项式.对于一个小函数a(z)即T(r,a)=S(r,ω),如果P(z,a)≢0,则在除去一个有限对数测度的集合上有

引理2.3 复平面上的函数f(z),如果满足条件

则称为超越亚纯的.

引理2.4 设F(z),P0(z),…,Pn(z)是多项式且满足FPnP0≢0,那么对于方程(2)或者(5)的任意有限级亚纯解f(z),有σ(f(z))≥1.

3 定理的证明

3.1 定理1.1的证明

设f(z)是方程(2)的有限级超越亚纯解,由定理C的结论可以得到σ(f(z))≥1.因此,只需要证明λ(f(z)-a(z))=σ(f(z))即可.

令g(z)=f(z)-a(z),由于σ(a)<1,所以g(z)是超越的且满足σ(g)=σ(f)≥1及S(r,g)=S(r,f).

将f(z)=g(z)+a(z)代入方程(2), 可得K(z,g)=Pn(z)g(z+n)+…+P1(z)g(z+1)+P0(z)g(z)+Pn(z)a(z+n)+…+P1(z)a(z+1)+P0(z)a(z)=0.所以,有K(z,0)=Pn(z)a(z+n)+…+P1(z)a(z+1)+P0(z)a(z).

下面证K(z,0)≢0成立，分两种情形：

情形1 当a(z)是超越亚纯函数时,如果上述结论不成立即K(z,0)≡0,由定理C可得σ(a)>1,这与条件σ(a)<1矛盾,故有K(z,0)≢0.

情形2 当a(z)是有理函数时, 如果上述结论不成立即K(z,0)≡0,由条件deg(Pn+…+P0)=max{degPj∶j=0,1,…,n}≥1,可知方程(2)不存在非零常数解.

设

(6)

式中:c≠0, cs-1, …, c0, d≠0, dt-1, …, d0是常数, s和t是非负整数且满足s+t≥1.由(6)可得

(7)

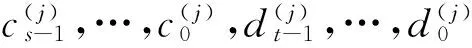
Pn(z)α(z)+…+P1(z)α(z)+P0(z)α(z)=0,

(8)

式中:αn(z),…,α0(z)是多项式,

(9)

因为αj(z)的第一项是cdnzs+nt,由方程(8)和方程(9)可知方程(8)的左边是一个多项式, 其次数为

s+nt+deg{Pn(z)+…+P1(z)+P0(z)}=s+nt+max{deg Pj(z)∶j=0,1,…,n}≥2.

显然与方程(8)矛盾.因此,方程(2)不存在非零有理解, 即K(z,0)≢0.

综合上述两种情形可知,

K(z,0)=Pn(z)a(z+n)+…+P1(z)a(z+1)+P0(z)a(z)≢0.

(10)

3.2 定理1.2的证明

假设 f(z)是方程(5)的超越亚纯解,由定理D可得λ(f)=σ(f)≥1.只需证明λ(f(z))-a(z))=σ(f(z)).

令g(z)=f(z)-a(z),由于σ(a(z))<1,所以g(z)是超越的且满足σ(g)=σ(f) ≥1及S(r,g)=S(r, f).将f(z)=g(z)+a(z)代入方程(5), 可得H(z,g)=Pn(z)g(z+n)+…+P1(z)g(z+1)+P0(z)g(z)+Pn(z)a(z+n)+…+P1(z)a(z+1)+P0(z)a(z)-F(z)=0,从而可得H(z,0)=Pn(z)a(z+n)+…+P1(z)a(z+1)+P0(z)a(z)-F(z),推断H(z,0)≢0.下面分两种情形对此结论进行证明.

情形1 假设a(z)只有有限多个极点.由σ(a(z))<1和引理2.1可知,存在一个ε-集合E使得当z→∞(z∈CE)时

a(z+j)=a(z)(1+oj(1)), j=1,2,…,n,

(11)

其中,oj(1)(j=1,2,…,n)满足当z→∞(z∈CE)时

oj(1)→0.

(12)

设H={|z|=r∶z∈E,|z|>1},可知H具有有限对数测度,将式(11)代入H(z,0)=0,可得当z→∞(z∈CE)时,

Pn(z)a(z)(1+on(1))+…+P1(z)a(z)(1+o1(1))+P0(z)a(z)=F(z),

(13)

从而可得

(14)

由于a(z)只有有限多个极点,可得当|z|=r∉H时,

T(r,a)= m(r,a)+N(r,a)=m(r,a)+O(ln r)=

从而可得T(r,a)=O(ln r), 这与a(z)是超越的相矛盾,所以H(z,0)≢0.

情形2 假设a(z)具有无穷多个极点.如果H(z,0)≡0,由引理2.4可得σ(z(z))≥1,这与σ(z(z))<1矛盾,故H(z,0)≢0.

综合以上两种情形有

H(z,0)=Pn(z)a(z+n)+…+P1(z)a(z+1)+P0(z)a(z)-F(z)≢0.

(15)

由引理2.2可得

(16)

从而

(17)

因此,λ(f(z)-a(z))=σ(f(z)),定理1.2得证.

关于推论1.1和1.2的结论很显然可以得到,此处不再证明.

[1] YANG C C,YI H X.Uniqueness Theory of Meromorphic Functions[M].The Netherlands:Kluwer Academicpublishers,2003.

[2] LAINE I.Nevanlinna Theory and Complex Differential Equations[M].Berlin:Walter de Gruyter,1993.

[3] HAYMAN W K.Meromorphic Functions[M].Oxford:Clarendon Press,1964.

[4] LAINE I,YANG C C.Clunie theorems for difference and q-difference polynomials[J].Journal of the London Mathematical Society,2007(76):556-566.

[5] BERGWEILER W,LANGLEY J K.Zeros of difference of meromorphic functions[J].Mathematical Proceedings of the Cambridge Philosophical Society,2007(142):133-147.

[6] ABLOWITZ M,HALBURD R G,HERBST B.On the extension of Painlevé property to difference equations[J].Nonlinearity,2000(13):889-905.

[7] ISHIZAKI K,YANAGIHARA N.Wiman-Valiron method for difference equations[J].Nagoya Mathematical Journal,2004 (175): 75-102.

[8] HALBURD R G,KORHONEN R J.Difference analogue of the lemma on the logarithmic derivative with applications to difference equations[J].Journal of Mathematical Analysis and Applications,2006(314):477-487.

[9] LI S,GAO Z S.Finite order meromorphic solutions of linear difference equations[J].Proceedings of the Japan Academy,Series A,2011(87):73-76.

[10]CHIANG Y M,FENG S J.On the Nevanlinna characteristic and difference equations in the complex plane[J].The Ramanujan Journal,2008(16):105-129.

[11]CHEN Z X.Growth and zeros of meromorphic solutions of some linear difference equations[J].Journal of Mathematical Analysis and Applications,2011(373):235-241.

[12]CHEN Z X,SHON K H.On growth of meromorphic solutions for linear difference equations[J].Abstract and Applied Analysis,2013(2013):41-62.

Some properties of the meromorphic solutions of linear difference equation

DU Yunfei，ZHAO Ming

(SchoolofMathematicsandSystemsScience,BeihangUniversity,Beijng100191,China)

We investigate the relationship between function of small growth and the order, the exponent of convergence of zeros of the meromorphic solution of difference equations Pn(z)f(z+n)+…+P1(z)f(z+1)+P0(z)f(z)=0 and Pn(z)f(z+n)+…+P1(z)f(z+1)+P0(z)f(z)=F(z), where F(z)，P0(z)，…，Pn(z) are polynomials, which generalize the related results.

difference equation; meromorphic solution; small function

2016-02-26

国家自然科学基金(11171013；11371225)

杜云飞(1986-),男,河南新乡人,博士研究生,主要从事复分析及其应用方面的研究.

O174.52

A

1674-330X(2016)02-0076-05