桥梁跨径对混凝土简支箱梁结构噪声的影响研究

张 磊，耿传智

（同济大学铁道与城市轨道交通研究院，上海201804）

桥梁跨径对混凝土简支箱梁结构噪声的影响研究

张 磊，耿传智

（同济大学铁道与城市轨道交通研究院，上海201804）

为探究桥梁跨径对结构噪声的影响，选取30 m 的混凝土箱梁为研究对象，采用有限元-边界元联合仿真技术进行数值仿真，并进行现场试验验证。在此基础上，通过改变桥梁跨径和改变桥梁结构体系，探讨了桥梁跨径对桥梁结构噪声的影响规律。研究结果表明：箱梁振动和噪声的峰值频率为50～63 Hz，减小桥梁跨径能降低结构噪声，增大跨径结构噪声先升后降；改变桥梁体系能够有效改善结构噪声水平。

城市轨道交通；桥梁跨径；结构噪声；有限元-边界元

0 引言

目前，城市轨道高架结构混凝土箱梁结构运用十分普遍，但随之而来的桥梁结构噪声问题并没有得到充分认识。以往高架结构跨度设计多考虑结构的力学性能，而忽略了结构噪声的影响。在满足力学性能的前提下，跨径变化对结构噪声的影响还有待研究。

通过增加桥梁结构刚度来减小桥梁结构振动，是一种降低声辐射的有效途径。Bewes 以混凝土桥、钢筋混凝土桥和钢桥为研究对象，探讨了桥梁某些结构组件的厚度对桥梁结构噪声的影响；韩江龙通过车线桥耦合振动分析研究桥梁振动响应，并通过模态叠加法研究了板厚和加肋对槽型梁结构噪声影响；J.H.Cooper 等对香港西铁的截面进行优化，箱梁质量减小30%，而且桥梁结构噪声级也降低。

以上研究均是对桥梁截面进行改造来改变桥梁刚度，通过在设计之初合理确定桥梁体系和桥梁跨径对结构噪声的影响还有待研究。本文通过有限元-边界元联合仿真技术对简支箱梁的结构噪声特性进行分析，并通过改变跨径和体系考察对声辐射的影响，为桥梁结构噪声研究提供参考。

1 场点声压与结构振动响应的关系

高架结构振动属于小幅振动，产生的结构噪声属于线性声学问题。桥梁结构辐射声场为外声场，满足Neumann 边界条件和 Sommerfeld 辐射条件，由此可得到结构在外部流体介质场 Q 中任意点P的稳态辐射声压p（P）：

式（1）中，rs是辐射面上某一点的位置矢量；R为结构表面位置矢量为rs的点到场点P的距离；；ρ为流体介质的密度；ω为圆频率；vn、p（rs）分别为结构表面位置矢量为rs点的法向的振动速度和声压；G（R）为自由空间格林函数，使用加权残值法可求得：

式（2）中，k=ω/c为波数；ω为圆频率；c为流体介质中的声速。

当外声场场点 P 无限接近结构表面时，得 Helmholtz表面积分方程：

将结构表面 S 划分为 N 个单元后，对 Helmholtz 方程在结构表面进行离散，可得到表面任意单元 m 的场点声压：

式（4）中，j 为单元序号；Sj为编号为 j 的单元的面积。

N 个单元，则可列出 N 个方程，写成矩阵形式可得直接边界元法的系统方程：

其中，A（ω）、B（ω） 为影响矩阵；ps为结构表面声压向量；vn为结构表面法向速度向量。

再对公式（1）以同样的方式将面 S 离散为 N 个单元，可求外部场点中任意点 P 的声压为：

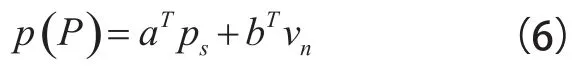
综合式（5）、式（6），可得：

2 理论计算与实验对比

2.1 结构概况

宁波轨道交通某跨径30 m 简支箱梁桥，高1.8 m、宽8.9 m、底板厚0.25 m、腹板厚0.5 m、顶板厚0.25 m、桥墩高度为5 m。桥面无声屏障遮挡，为全预应力结构，混凝土强度等级 C50，承轨台和桥面板整体浇注。为了考察梁底不同高度以及距离线路中心线不同距离的声场变化情况，选取如图1所示的场点布置。

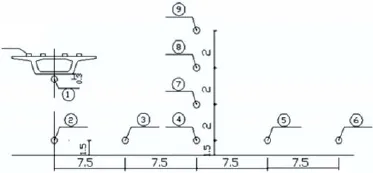
图1 场点布置图（单位：m）

2.2 仿真模拟

应用 Simpack 建立车轨耦合模型。依据实际情况，本文采用6节 A 型车辆编组，实测车速59.6～61.5km/h，计算车速60km/h，轨道不平顺采用美国功率谱。Simpack 中可以通过输入不平顺功率谱密度的系数直接生成轨道不平顺，取采样间距0.1 m，钢轨计算长度共采集样本1200个，频率带宽0.01 Hz，则生成的美国六级谱垂向不平顺样本曲线如图2。

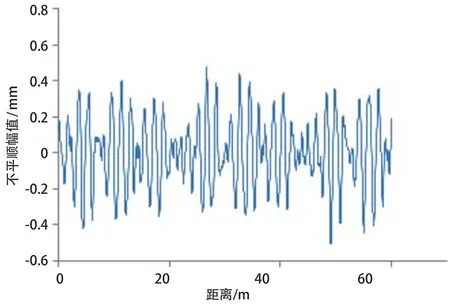
图2 美国六级谱垂向不平顺样本曲线

应用 ANSYS 有限元建立轨道桥梁有限元模型，为保证边界条件，钢轨延长至120 m。模型中，钢轨采用Beam188单元模拟，箱梁和承轨台采用8节点实体单元 Solid45模拟，扣件系统采用间距为0.6 m 的离散弹簧阻尼单元 Combin14模拟。扣件刚度50 MN/m，阻尼75 kN·s/m。单元最大尺寸为0.6 m，满足精度要求。

声学分析采用Virtual-Lab商用软件，为满足Neumann 边界条件，边界元网格在梁体两端进行封闭。研究结构噪声取截至频率 fmax=250 Hz，声学单元尺寸为0.2 m，满足单元边长 d≤c/6fmax的要求（c 为流体介质中的声速）。

2.3 计算与实测对比分析

图3给出了实测与计算的1/3倍频程声压级曲线，由图3可知：

（1）各测点的实测与计算声压频率曲线比较接近，表明有限元-边界元联合仿真的方法适用于桥梁结构噪声的计算；

（2）计算声压在80 Hz 及以后相较实测值偏低，是由于仿真理想化了扣件单元的性能，导致80 Hz 及以后的轮轨荷载过滤过多，较少传递到桥梁结构；

（3）桥梁结构噪声在31.5～63 Hz 之间幅值较大，这与结构振动响应是吻合的；

（4）31.5 Hz 之前的实测与计算结果差异可能由于模型中地面作为全反射面来考虑而引起。

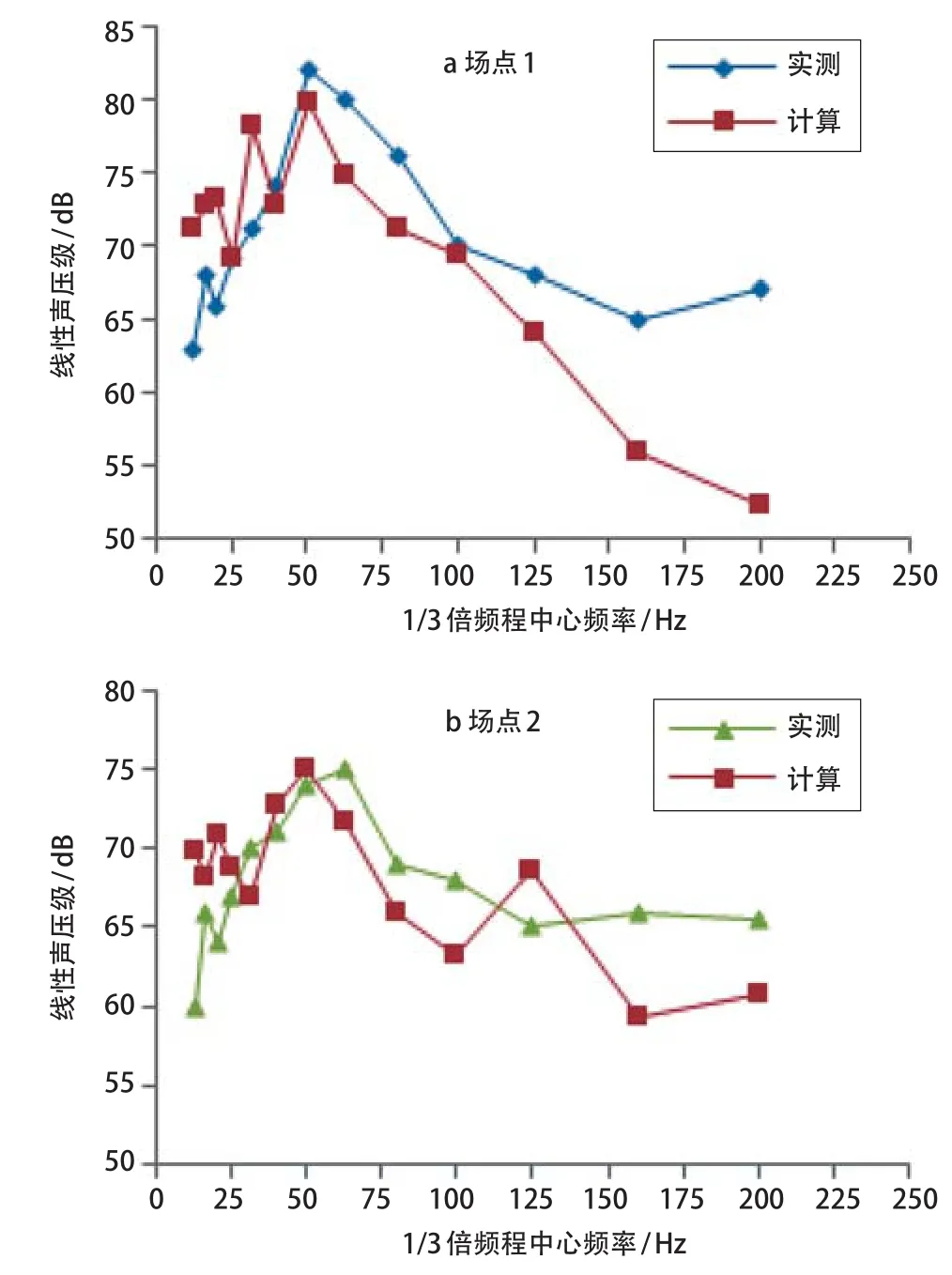
图3 实测与计算对比

3 跨径对结构噪声的影响

3.1 跨径长度的影响

为了考察跨径对箱梁结构噪声的影响规律，以该箱梁为参照，仅改变桥梁跨径，跨径分别取18、24、27、33、36、42m，并计算同等条件下的跨中对应场点结构噪声。各跨径桥梁场点噪声最大声压级水平如表1。

通过表1可以看出，不同跨径桥梁结构噪声的传播具有以下共同特点：由2～6号场点声压变化可知，随着声压测点距离的增加，结构噪声逐渐减弱，并近似呈线性变化；由4、7、8、9场点声压变化可知，结构噪声在高度方向变化规律较复杂，在桥面以下随着距离的增加而减小，在桥面以上呈略微增加，这可能由于桥面上方受桥梁顶板噪声直射的影响。

表1 场点线性声压级 dB

跨径长度对结构噪声的影响比较复杂。对比表1可以看出，原桥梁跨径减小6 m，各场点结构噪声均减小2.4～3.3 dB，继续减小跨径，各场点的结构噪声减少1.3～2.5 dB；原桥梁跨径增加6 m，各场点结构噪声约增大0～1.5 dB；继续增大跨径6 m，相较原桥梁，各场点的结构噪声均减少2 dB 左右；桥梁跨径增大或减小3 m，结构噪声增幅或减幅基本在1 dB 之内。

为进一步分析跨径长度对结构噪声的影响，参照文献[1]的成果：“振动结构噪声辐射功率由振动响应和噪声辐射效率共同决定”，本文从噪声辐射效率和振动响应两个因素对结构噪声随跨径的变化做出分析。

3.1.1 噪声辐射效率

噪声辐射效率是描述振动物体向外辐射噪声能力的指标，是频率的函数。图4为有限平板噪声辐射效率级的近似设计曲线，图4中，fc为吻合频率．即达到最大噪声辐射效率级y2的频率，对应的波长为λc，fc、y2按式（8）计算：

式（8）中，c为流体中的声速；ρ为板的面密度；D为板的弯曲刚度；δ、L分别为有限平板的厚度和周长。

由式（8）可知，改变跨径不改变吻合频率，根据结构概况可计算不同跨径各箱梁板的吻合频率均为fc=64.6 Hz。但桥梁面板周长的变化对噪声辐射效率级有影响，以桥梁顶板为例，不同跨径箱梁最大噪声辐射效率级差 Δy2为：

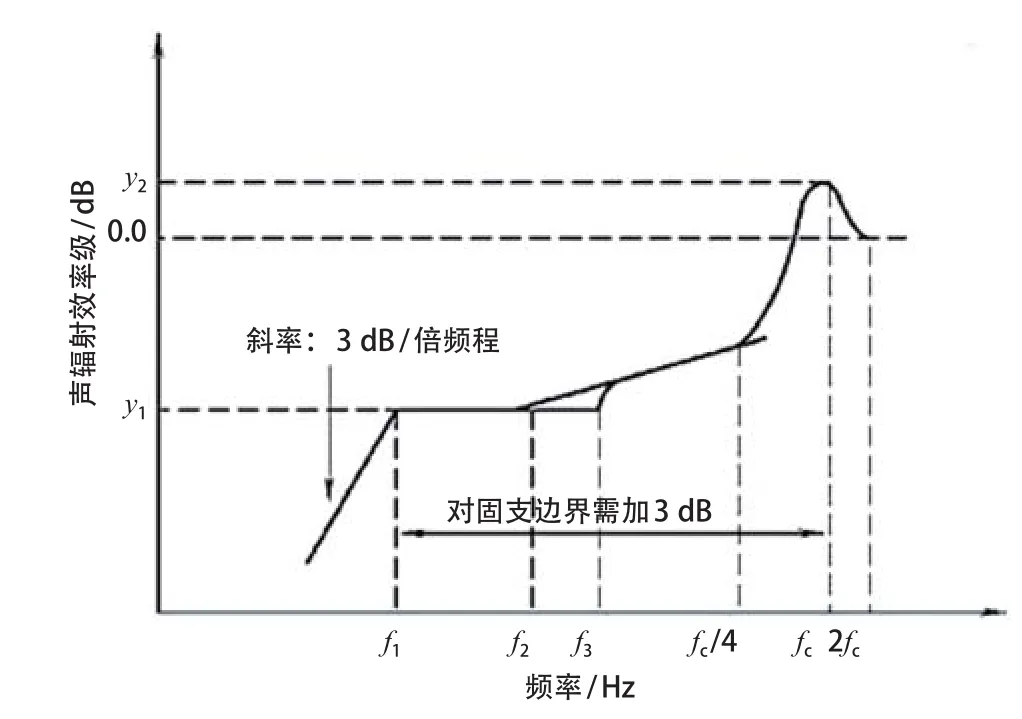
图4 有限平板声辐射效率级的近似设计曲线

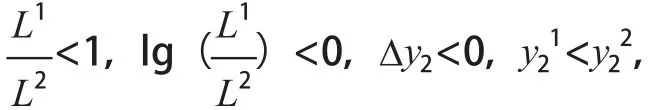
3.1.2 振动响应

图5为增大桥梁跨径和减小桥梁跨径各方案箱梁顶板跨中中点振动加速度级曲线。在0～50 Hz，振动加速度级随频率增加急剧增大，在50～80 Hz 频带内，结构振动加速度较大，且在50～63 Hz 出现峰值，在80 Hz 之后，振动加速度幅值平缓下降。

在图5中，对比不同跨径箱梁加速度级曲线可知，随着跨度的减小，顶板振动加速度级逐渐减小，并且随着跨径的减小，顶板振动加速度级峰值频率从50 Hz逐渐向63 Hz 移动；随着跨径的增大，顶板振动加速度级逐渐增大，峰值频率逐渐从50 Hz 向40 Hz 移动，且在50～80 Hz 间30、33、36 m 跨径的桥跨振动级差别不大，42 m 跨径在50～80 Hz 段振动响应反而较其他跨径桥梁振动加速度级低。

图5 顶板跨中中点振动加速度级

综上，减小桥梁跨径，结构振动响应减小，且最大噪声辐射效率级降低。所以能够减小结构噪声水平；增大桥梁跨径，结构振动响应增大，但主要是40 Hz 之前的低频段，由有限平板噪声辐射效率级的近似设计曲线可知，该频段远离吻合频率64.6 Hz，噪声辐射效率低，对噪声辐射影响相对较小，所以30、33、36 m 跨径简支桥梁结构噪声差别不大；继续增大桥梁跨径，振动能量主要在低于50 Hz 的低频段振动响应继续增大，但噪声辐射效率较高的50～80 Hz 段振动响应反而减小，所以结构噪声会有所降低。

3.2 桥梁体系的影响

对原有简支梁桥方案跨中增设支座，转变为两跨连续梁桥体系，并计算同等条件下的结构噪声。各场点最大声压如图6，由图6可以看出，将简支梁桥跨中增设支座，改造成两跨连续梁体系，场点声压具有相同的变化规律，每个场点约有4 dB 的降噪效果。

图6 改变体系前后各场点声压级

4 结论

通过对30 m 混凝土简支箱梁桥结构噪声分析，可以得到以下结论。

（1）有限元-边界元联合仿真的方法适用于桥梁结构噪声的分析。

（2）在远离桥梁中心线方向，结构噪声呈线性衰减，但在高度方向，在桥面上下方变化不一致。

（3）跨径的改变会对结构噪声产生影响。基于现有30 m 跨径简支梁桥，适当减小跨径有利于减小结构噪声；增大跨度虽然也能减小噪声，但应综合考虑城市轨道交通桥梁的刚度要求；改变桥梁体系能显著改善结构噪声。

[1] Wu X. Experimental validation of finite element and boundary methods for predicting structural vibration and radiated noise [D].USA: the University of Kentucky,1991.

[2] 韩江龙，吴定俊，李奇. 板厚和加肋对槽型梁结构噪声的影响[J]. 振动工程学报，2012，25（5）：589-594.

[3] 李宝银，杨宜谦. 铁路和地铁桥梁结构噪声研究[J].土木建筑与环境工程，2013（增2）：28-32.

[4] Cooper J H.Harrison M F. Development of an alternative design for the West Rail viducts[J]. Proceeding of Institution of Civil Engineers, Transport,2002,153（2）：87-95.

[5] 李小珍，张迅，刘全民，等. 铁路32米混凝土简支箱梁结构噪声试验研究[J]. 中国铁道科学，2013，34（3）：20-28.

[6] 高飞，夏禾，曹艳梅，等. 用边界元-有限元法研究高架结构辐射噪声[J]. 土木建筑与环境工程，2012，34（1）：34-43.

[7] 丁勇，布占宇，谢旭．考虑桥面板振动的桥梁结构低频噪声分析[J]．土木建筑与环境工程，2011，33（2）：58-64．

[8] AuF T K, Wang M F. Sound radiation from forced vibration of rectangular orthotropic plates under moving loads[J]. Journal of Sound and Vibration,2005,281（3）：1057-1075.

[9] Bewes O G. The calculation of noise from railway bridge and viaducts [D]. USA: University of Southampton,2005.

[10] 张迅，李小珍，刘全民，等．混凝土箱梁的结构噪声及其影响因素[J]．西南交通大学报，2013，48（3）：409-414．

[11] 李小珍，张迅，刘全民，等.高速铁路桥梁结构噪声的全频段预测研究（Ⅱ）：试验验证[J]. 铁道学报，2013，35（2）：87-92.

[12] 张升明，潘旭初. 板架结构的振动噪声研究[J]. 振动与噪声控制，1995（5）：9-13.

责任编辑 朱开明

Inf uence of Bridge Span on Structural Noise of Concrete Simply Supported Box Girder

Zhang Lei, Geng Chuanzhi

In order to identify the influence of bridge span on structural noise, the30m concrete box girder is chosen in the research work, the finite element and boundary element combined simulation technology is used to simulate the structure, and the field test is carried out. On this basis, the influence of bridge span on the bridge structure noise is discussed by changing the bridge span and changing the bridge structure system. The results show that the peak frequency of the vibration and noise of the box girder is50-63Hz, reducing the noise by reducing span of bridge and span structure, increasing the noise at fi rst and then decreasing the noise. The change of bridge system can effectively improve and control the structure noise level.

urban rail transit, rail transit, bridge span, structural noise, fi nite element-boundary element

U488.213

2016-04-20

张磊（1992—），男，硕士研究生