复杂约束条件下再入高超声速滑翔飞行器轨迹快速优化①
2017-01-05邢清华毛艺帆
王 路,邢清华,毛艺帆
(空军工程大学 防空反导学院,西安 710051)
复杂约束条件下再入高超声速滑翔飞行器轨迹快速优化①
王 路,邢清华,毛艺帆
(空军工程大学 防空反导学院,西安 710051)
作为直接法的典型代表,高斯伪谱方法在处理复杂约束条件(含路径点或禁飞区约束)下再入高超声速滑翔飞行器轨迹优化问题时,仅能保证所得轨迹在各高斯节点处严格满足各项约束,而节点之间轨迹的可行性无法保证,为解决这一问题,文章提出改进多阶段高斯伪谱方法。该方法首先使用新定义的两类节点(固定节点和虚拟节点)将轨迹分段,其中固定节点是用来保证路径点与高斯节点重合,虚拟节点则是用来保证禁飞区附近分布更多的高斯节点,此分段方式能保证所得轨迹在任意位置可行;然后,向各分段轨迹插入指定数目的高斯节点;最后,使用序列二次规划方法对此多阶段轨迹优化模型进行求解。仿真结果表明,改进多阶段高斯伪谱方法在处理复杂约束条件下再入高超声速滑翔飞行器轨迹优化问题时快速有效。
再入高超声速滑翔飞行器;轨迹优化;路径点;禁飞区;高斯伪谱方法
0 引言
高超声速滑翔飞行器因其高升阻比外形设计具有良好的气动性能,能凭借空气动力的作用,实现远距离无动力滑翔飞行。由于飞行器运动方程形式复杂、再入滑翔轨迹对控制量敏感,且飞行过程中受过载、热流密度等约束影响较大,其轨迹优化问题一直是研究的热点。
通常轨迹优化的数值解法从本质上可分为直接法和间接法[1]。间接法根据一阶最优必要条件和庞特里亚金最小化原理,将最优化问题转化为两点边值问题[2],缺点是对初值高度敏感,很难收敛,时效性不高。而直接法将原始最优控制问题转化为非线性规划问题,在求解过程中具有较大的收敛半径,且不受一阶必要条件的限制[3]。
作为直接法中的典型代表,高斯伪谱方法使用少量的节点,并具有较快的收敛速度,目前已被广泛应用于普通约束条件下高超声速飞行器上升段[4]或再入段[5-11]的轨迹优化问题,这里的普通约束主要包括动压、过载、热流密度等过程约束、控制约束及终端状态约束。然而,在飞行器实际再入过程中,不得不考虑某些真实约束,如路径点和禁飞区约束。路径点是指侦察或载荷投送时,飞行器必须经过的空间位置,禁飞区是指受地理政治或敌方武器系统威胁,飞行器应严格避让的某些特殊区域。
高斯伪谱法将状态变量和控制变量在一系列高斯节点上离散,所有约束条件在高斯节点上严格满足,但高斯节点的分布呈中间疏松、两端密集的特点。此时,考虑路径点和禁飞区约束条件,可能会带来以下问题:
(1)相邻高斯节点之间的轨迹不一定满足禁飞区约束或过程约束;
(2)路径点约束条件不一定能够满足高精度。
针对问题1和问题2,Jiang[12]提出了基于高斯伪谱方法的多阶段轨迹优化技术,通过所提出的3类插入点,将整个再入轨迹划分为不同阶段,由于其所设计的3类插入点都是固定的,所以最终得到的轨迹必须严格经过各插入点。但通过研究发现,在轨迹生成之前,只有路径点是确定的,而禁飞区附近的飞行轨迹是未知的,所以只有路径点可提前设置为固定插入点,Jorris[13-14]和Hu[15]所研究的轨迹优化问题考虑了路径点和禁飞区等复杂约束条件,但没有具体讨论高斯伪谱方法存在的上述两类问题。针对以上问题,还有一类解决方法,就是使用大量的高斯节点对问题进行求解,但代价是十分耗时,实用价值不强。
为克服传统高斯伪谱方法在处理复杂约束条件下轨迹优化问题时存在的不足,本文提出改进多阶段高斯伪谱方法,通过使用新定义的两类节点(固定节点和虚拟节点)将轨迹分段,在不增加总节点数目的同时,改变节点的分布。一方面,使路径点与高斯节点重合,从而保证路径点约束被严格满足;另一方面,是禁飞区附近分布高密度的高斯节点,从而保证禁飞区约束满足要求,又由于节点数目并没有增加。所以,可保证所提算法的快速性。仿真结果验证了其有效性。
1 问题描述
本节主要介绍高超声速飞行器再入轨迹优化问题模型,包括再入动态方程、约束条件和目标函数。
1.1 再入动态方程
在高超声速飞行器的再入阶段,假设目标为质点,并将地球视为非旋转匀质球体,则飞行器再入运动方程如下[16]:
(1)
式中V为飞行器速度,m/s;θ为航迹倾角,rad;ψ为航迹偏角,rad;r为飞行器质心至地心的距离,m;λ为地理经度,rad;φ为地理纬度,rad;γc为滚转角,rad;m为飞行器质量,kg;D为阻力,D=CDρSV2/2;L为升力,L=CLρSV2/2;CD为阻力系数;CL为升力系数;S为气动参考面积。
在高超声速条件下,升力、阻力系数CL、CD可近似表示为攻角α(°)与速度V(Ma)的函数[17]。
(2)
式中CLi和CDi(i=0,…,3)为常系数。
1.2 约束条件
1.2.1 过程约束
高超声速飞行器再入滑翔阶段是一个高动态的过程,为满足系统热防护和结构稳定性的需要,再入过程需满足一系列苛刻约束条件的限制,如动压限制、热流密度限制、过载限制。
(3)

1.2.2 控制约束
为了保证系统的稳定性与可控性,攻角与滚转角应满足如下约束:
(4)
式中 下标“min”与“max”为对应变量的下限与上限。
1.2.3 终端约束
为使飞行器具备一定的末段打击能力,对终端约束条件也应进行一定的限制。
(5)
式中 下标“f”为终端状态。
1.2.4 路径点与禁飞区约束
路径点约束:为了完成诸如侦察或载荷投掷等特定任务,飞行器需精准的飞过指定路径点上空,对应路径点约束表示如下:
(6)
式中Npoint为路径点的总个数。
禁飞区约束:受地理政治或敌方武器系统威胁的限制,飞行器应严格避让某些特殊区域,在此假设禁飞区为不限高度的圆柱体[13],第j个禁飞区的中心点坐标用(λj,φj)表示,对应的禁飞区半径用Rj表示,则禁飞区约束表示为
(7)
式中Nzone为禁飞区的个数。
1.3 目标函数
通常情况下,不同的任务对应不同的目标函数。如果是为了维持飞行器较好的热防护,目标函数可设置为最小热流密度或最小峰值热流密度;如果打击或终点目标是固定的,目标函数可设置为达到时间最短;而如果是为了测试飞行器的性能,目标函数可设置为横向或纵向航程最大等等。
1.4 轨迹优化
对于高超声速飞行器,其再入轨迹优化问题就是寻找控制量α和γ,在满足各项约束条件的同时,使得目标函数最优。
2 改进多阶段高斯伪谱方法
2.1 高斯伪谱法及其分析
2.1.1 高斯伪谱法
可用一般最优控制问题描述高超声速飞行器再入轨迹优化问题,这里采用Bolza问题形式[18]进行表述。连续Bolza问题可描述为:求解控制变量u(t)∈Rm和状态变量x(t)∈Rn,使如下目标函数[7]最小化。
(8)
同时满足如下运动方程、过程约束以及终端约束:
(9)
式(8)、式(9)被称为连续Bolza 问题的数学描述。高斯伪谱法在高斯节点上将状态变量和控制变量进行离散,并利用这些离散点构造全局拉格朗日插值多项式来近似系统的动力学方程,从而将连续的无限维最优控制问题转换为非线性规划问题进行求解[19]。对于高超声速飞行器,飞行持续时间为从t0到tf,而高斯节点的分布区间为[-1,1]。因此,需将时间区域从t∈[t0,tf]转化至τ∈[-1,1],转化公式如式(10):
(10)
需要注意的是,N个离散的节点包含了初始节点τ0=-1、终端节点τf=1以及K=N-2个内部节点,且这K个节点为K阶拉格朗日插值多项式的根,则状态和控制变量可近似表示如下:
(11)
其中,Li(τ)和Li*(τ)分别为N+1和N阶拉格朗日插值多项式的基函数,计算公式如下:
(12)
为获得动态运动方程的约束,对式(11)求导可得
(13)
高斯伪谱方法中每个节点处目标状态变量的倒数都应满足式(13)。微分矩阵D∈RN×N+1可离线生成,其各元素计算公式如下[20]:
式中PN(τ)为N阶拉格朗日插值多项式;i=1,2,…,N;k=1,2,…,N。
然后,将式(9)所述动态方程约束转化为如下等式约束:
其中,k=1,2,…,N。由于式(12)只表示高斯节点的目标状态,不包括初始时刻和终端时刻的目标状态,因此应增加2个端点处的等式约束如下[21]:
(16)
式中ωk为高斯积分的权重。
然后,目标函数中的积分项通过高斯积分近似,则目标函数可表示为
(17)
同时,可将终端约束和过程约束表示为
至此,将最优控制问题转化为非线性规划问题,描述如下:求解非线性规划问题的变量:
(19)
在满足式(15)、式(16)和(式18)所述约束条件的同时,使得式(17)所述目标函数达到最小。
2.1.2 分析
如图1所示,高斯节点的分布呈中间疏松两端密集的特点。

图1 拉格朗日高斯节点分布示意图Fig.1 Distribution of LG nodes
高斯节点的这种分布特性会带来以下几方面的问题:
(1)当高斯节点数目确定时,节点的分布位置在区间[-1,1]是确定的,如图2所示,由于约束条件只在节点处严格满足,所以很难保证所生成轨迹满足路径点约束,除非路径点和某一高斯节点恰好重合。
(2)如图3所示,尽管禁飞区约束在所有高斯节点均严格满足,但高斯节点之间的飞行器轨迹穿过了禁飞区。
(3)过程约束条件不能保证严格满足,如图4所示。尽管某项过程约束指标在所有高斯节点均严格满足,但该指标在多处超出了允许范围,这会为飞行器维持其结构的稳定性带来严重挑战。
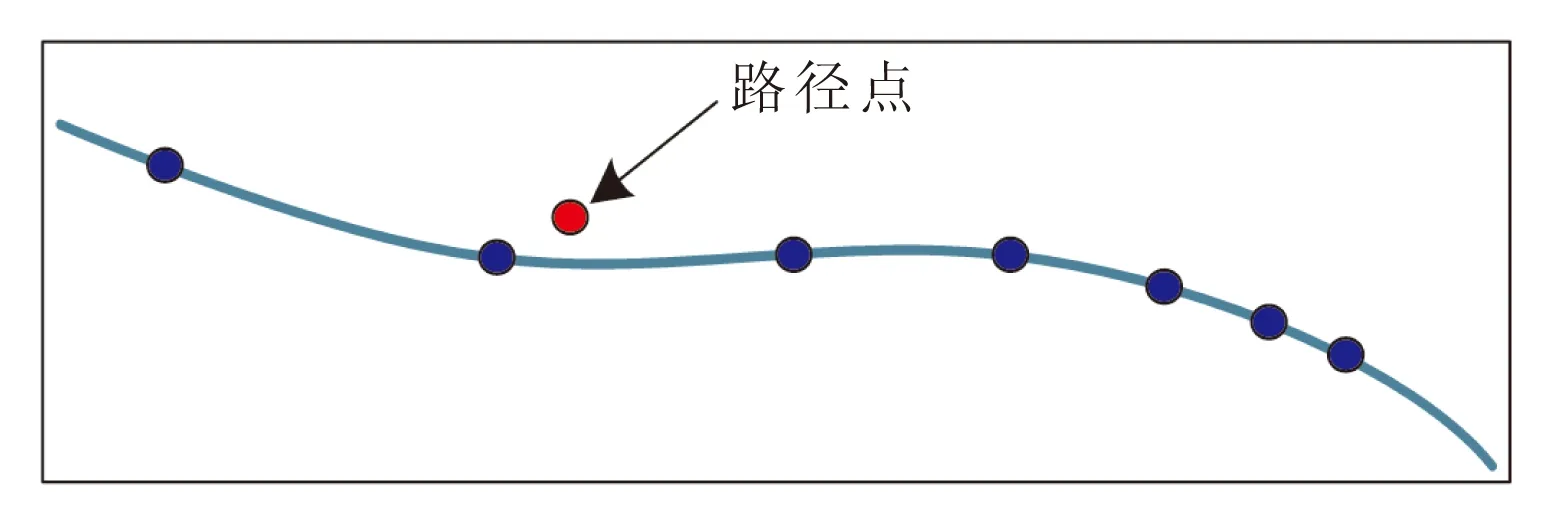
图2 路径点附近轨迹示意图Fig.2 Example of trajectory near the waypoints

图3 禁飞区附近轨迹示意图Fig.3 Example of trajectory near the no-fly zone

图4 过程约束变化示意图Fig.4 Change flow of path constraint
2.2 改进多阶段高斯伪谱算法
为克服前文所述传统高斯伪谱方法在处理复杂约束条件下的轨迹优化问题时存在的问题,本节提出改进多阶段高斯伪谱算法。
2.2.1 相关定义
定义1 固定节点:只包含位置信息,不包含时间信息的节点,如路径点。
定义2 虚拟节点:只含时间信息,不包含位置信息的节点。
2.2.2 算法流程
(1)步骤1 使用固定节点将轨迹划分为多阶段
如图5所示,将路径点设置为固定节点,使用固定节点将轨迹划分为多阶段,如此以来,路径点约束可严格满足。转步骤2。

图5 轨迹分段示意图(使用固定节点)Fig.5 Trajectory divided by fixed nodes
(2)步骤2 模型求解
假设轨迹被划分为Z段,每阶段的高斯节点数目为N,则第z阶段的目标函数可表示为
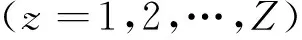
(20)
则总目标函数可表示为
(21)
对应的终端和过程约束表示为
(22)
式(15)转变为
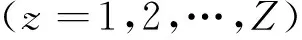
(23)
式(16)转变为
(24)
为保证各阶段连接点处的连续性,增加如下约束:
(25)
至此,式(20)~式(25)将传统高斯伪谱法转化为多阶段高斯伪谱法。模型的处理方式同传统高斯伪谱法一致,本文选用适用于求解大规模非线性规划问题的序列二次规划方法。
模型求解后,得到当前最优轨迹,转步骤3。
(3)步骤3 轨迹可行性判别

(26)
经检测如果各约束条件在所有检测点处严格满足,则停止,所得轨迹即为最优轨迹;否则,转步骤4。
(4)步骤4 增加虚拟节点将轨迹划分为多阶段
步骤3中不满足约束条件的检测点由于只包含时间信息,因此将其视为虚拟节点,如图7所示。轨迹被固定节点和新增虚拟节点划分为多阶段,由于高斯节点的分布特性,在虚拟节点的周围会有较多的高斯节点分布,通过这种方式,可保证过程约束或路径约束得到满足。然后,转步骤2。

图6 高斯节点和检测点分布示意图Fig.6 Distribution of LG nodes and checkpoints

图7 虚拟节点插入后禁飞区约束得到满足示意图Fig.7 No-fly zone constraint being satisfied by inserting virtual node
2.2.3 初值生成算法
本文使用传统的初始化策略:先采用较少的高斯节点,求解出一条低精度的轨迹;然后,通过对此低精度轨迹进行插值,得到理想数目高斯节点所对应的各节点初始值。
2.2.4 改进多阶段高斯伪谱法分析
改进多阶段高斯伪谱法主要思想为:首先将路径点视为固定节点,并用固定节点将轨迹分段,进行求解,从而使得到的轨迹严格满足路径点约束条件;为使全局轨迹严格满足禁飞区和路经约束,需要对所生成轨迹进行可行性验证,若不满足要求,则需增加虚拟节点,将轨迹重新分段,并进行求解,直至所生成轨迹严格满足所有约束条件后即可。
相比传统高斯伪谱方法,改进多阶段高斯伪谱方法在处理复杂约束条件下的轨迹优化问题时,具有如下优势:
(1)通过使用固定节点,将轨迹进行分段,所得轨迹严格满足路径点约束条件。
(2)通过使用虚拟节点,将轨迹进行分段,所得轨迹不仅在高斯节点处严格满足禁飞区以及过程约束,高斯节点之间的可行性同样可保证。
(3)固定节点和虚拟节点的加入,没有改变高斯节点的数目,而是改变了高斯节点的分布。所以,算法的速度没有受到影响。
3 仿真及分析


表1 初始时刻及终端时刻飞行器状态Table 1 Initial and terminal condition of vehicle

表2 路径点与禁飞区参数设置Table 2 Parameters of waypoint and no-fly zone constraints
3.1 粒子群算法仿真结果
粒子的数目为20,其他参数设置与文献[22]一致,所得最优轨迹如图8所示。
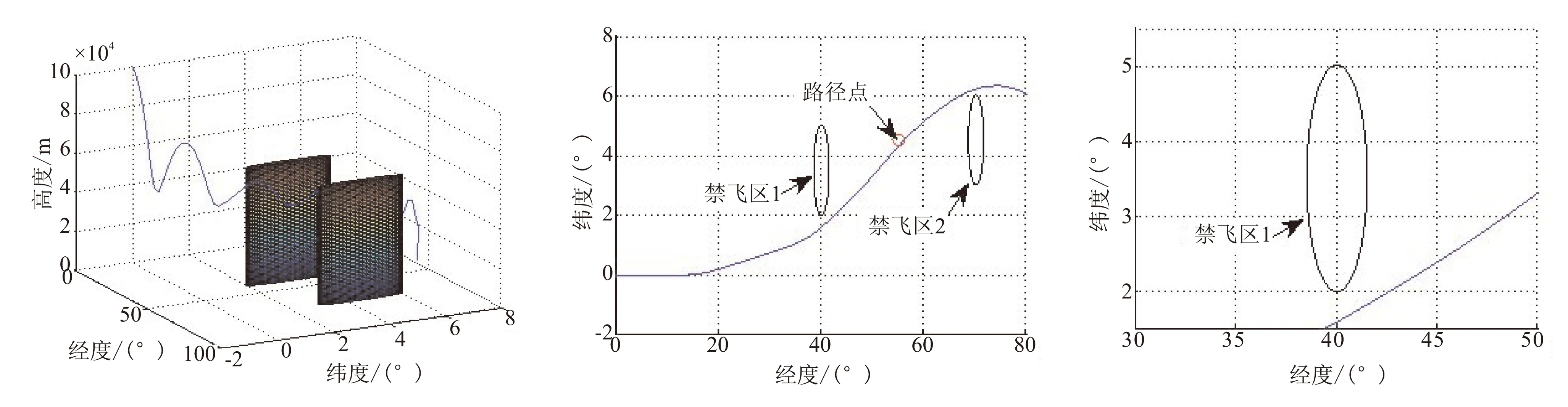
(a) 三维轨迹 (b) 俯视轨迹 (c) 禁飞区1附近轨迹
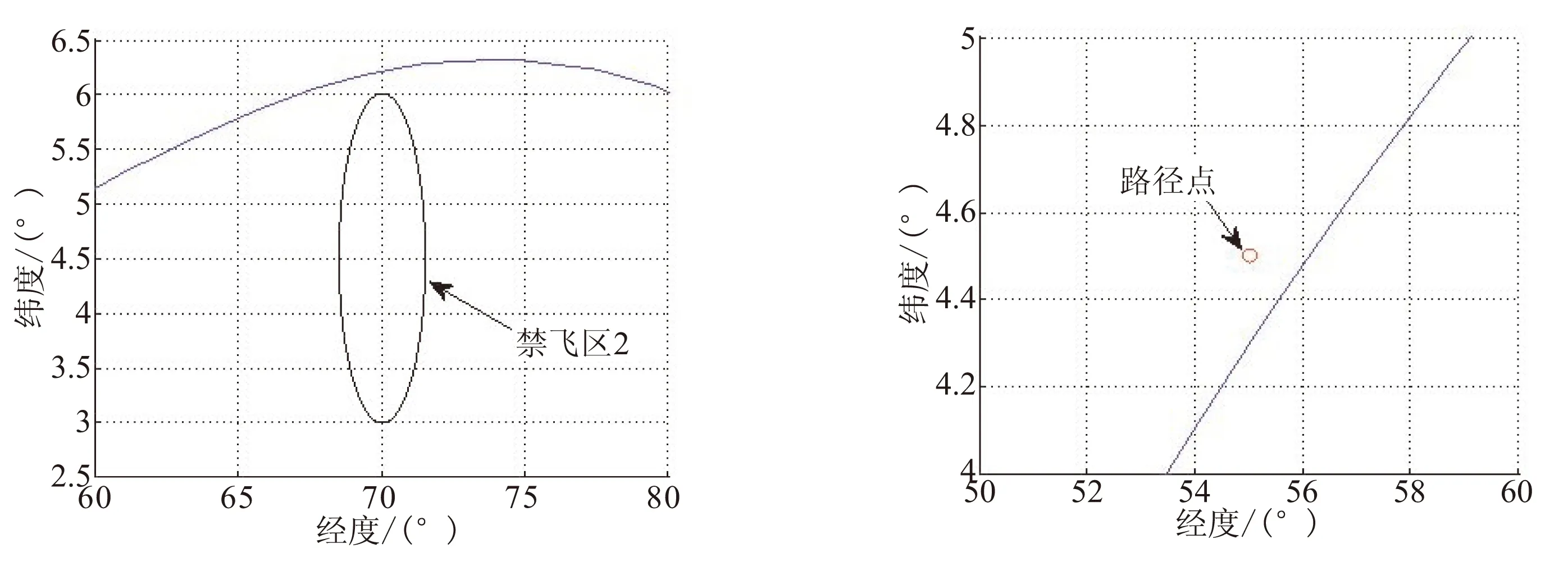
(d) 禁飞区2附近轨迹 (e) 路径点附近轨迹图8 粒子群算法仿真结果Fig.8 Results of optimal trajectory by PSO
3.2 传统高斯伪谱方法仿真结果
高斯伪谱方法选用的高斯节点数目为30,仿真结果如图9所示。

(a) 三维轨迹

(b) 俯视轨迹

(d) 禁飞区2附近轨迹图9 高斯伪谱方法仿真结果Fig.9 Results of optimal trajectory by GPM
3.3 改进多阶段高斯伪谱方法仿真结果
为与传统高斯伪谱方法进行比较,改进多阶段高斯伪谱方法所选取的高斯节点数目同样为30,仿真结果如图10所示。

(a) 三维轨迹

(b) 俯视轨迹
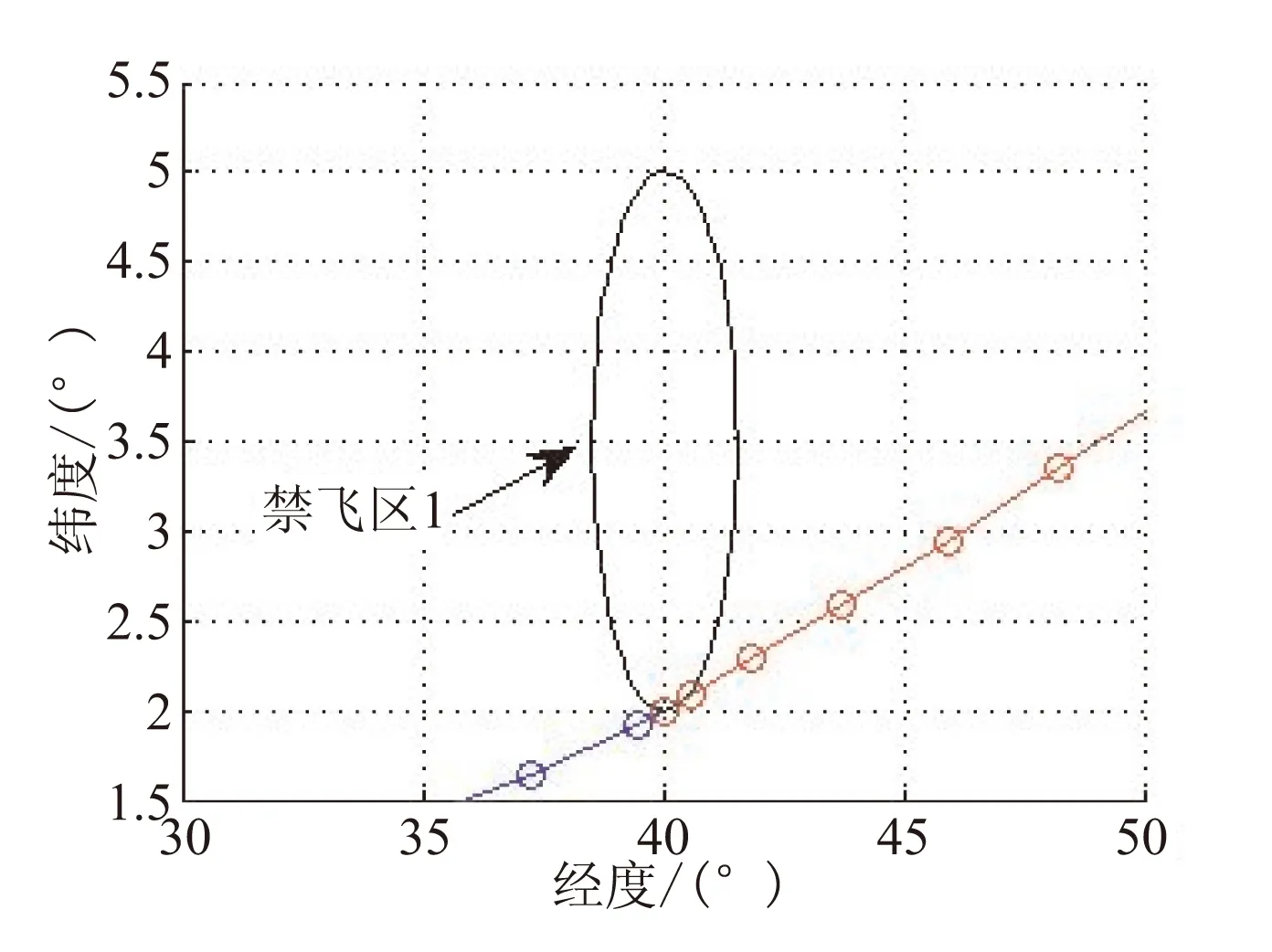
(c) 禁飞区1附近轨迹

(d) 禁飞区2附近轨迹图10 改进多阶段高斯伪谱方法仿真结果Fig.10 Results of optimal trajectory by improved GPM
3.4 仿真分析
由图8(a)、(b)可看出,所得轨迹较为平滑,图8(c)、(d)说明禁飞区约束能够严格满足,图8(e)说明路径点约束不能满足。
图9(a)给出了飞行器的三维运动轨迹。可见,所得轨迹较为平滑。图9(b)~(d)显示出了传统高斯伪谱方法的不足,即只能保证所得轨迹在高斯节点处严格满足约束条件,而无法保证其他部分的轨迹是否满足禁飞区等复杂约束。
由图10给出的仿真结果可见,通过使用固定节点和虚拟节点将轨迹分为了4段,而总的高斯节点的数目没有增加,只是改变了高斯节点的分布,所得轨迹严格满足路径点与禁飞区约束。
此外,粒子群算法求得最终飞行器飞行时间为1 592 s,传统高斯伪谱方法和改进高斯伪谱方法的最终结果分别为1 540 s和1 563 s。由此可见,高斯伪谱方法和改进高斯伪谱方法的精度都优于粒子群算法,相比改进高斯伪谱方法,传统高斯伪谱法虽然求得的目标函数值更小,但由于所得轨迹穿越了禁飞区,因此轨迹无法使用。
最后,分析不同仿真方法的耗时。粒子群算法的平均耗时约为2 min,但所得轨迹也只是接近全局最优;高斯伪谱方法的耗时约为1 min,但30个高斯节点不能保证节点之间的轨迹满足约束条件,如果将高斯节点的数目增加,虽然所得轨迹精度会提高,但仿真耗时同样会提高;相比之下,同样是30个高斯节点,但本文所提算法的耗时为30 s。这是由于固定节点的插入将路径点约束转化成了终端约束,而虚拟节点的插入将禁飞区约束只在某分段模型中进行求解,而传统高斯伪谱方法是将路径点和禁飞区约束在整个模型中进行求解。因此,本文所提算法耗时较小,且精度更高。
从以上仿真结果,可得出以下结论:
(1)使用固定节点将轨迹进行分段,所生成轨迹能够严格满足路径点约束;
(2)使用虚拟节点将轨迹进行分段,会有更多的高斯节点分布于虚拟节点附近,从而实现所生成轨迹能严格满足禁飞区约束和过程约束;
(3)所提出的改进多阶段高斯伪谱算法只是改变了高斯节点的分布,而没有增加高斯节点的数目。因此,相比其他类型多阶段伪谱方法,本文所提算法复杂度明显降低。
4 结论
为解决复杂约束条件下再入高超声速滑翔飞行器轨迹优化问题,本文提出改进多阶段高斯伪谱方法。通过使用固定节点和虚拟节点,将轨迹进行分段,在不增加高斯节点数目的前提下,改变了高斯节点的分布,以实现路径点和禁飞区附近有较多的高斯节点分布。仿真结果表明,所得轨迹具有较高的精度,各项约束条件能够严格满足。
[1] Huntington G T, Benson D, Rao A V. A comparison of accuracy and computational efficiency of three pseudospectral methods[C]//Proc. of the AIAA Guidance, Navigation, and Control Conference and Exhibit.2007, AIAA 20-23.
[2] Guo Xiao, Zhu Ming. Direct trajectory optimization based on a mapped Chebyshev pseudospectral method[J]. Chinese Journal of Aeronautics, 2013, 26(2):401-412.
[3] Ross I M, Fahroo F B. A perspective on methods for trajectory optimization[R].AIAA 2002-4727.
[4] Bailing Tian. 3DOF ascent phase trajectory optimization for aircraft based on adaptive gauss pseudospectral method[C]//2012 Third International Conference on Intelligent Control and Information Processing, 2012: 431-453.
[5] 孙勇,张卯瑞,梁晓玲. 求解含负责约束非线性最优控制问题的改进Gauss伪谱法[J]. 自动化学报,2013,39(5):672-678.
[6] 陈琦,王中原,常思江. 基于Gauss伪谱法的滑翔弹道快速优化[J]. 弹道学报,2013,21(15):105-108.
[7] 李柯,聂万胜,冯必鸣. 助推-滑翔飞行器弹道分段优化研究[J]. 指挥控制与仿真,2012,34(5):21-25.
[8] 汤亮,杨建民,陈风雨. 多约束条件下升力滑翔式再入轨迹优化[J].导弹与航天运载技术,2013(1):1-5.
[9] 曹红锦,葛致磊. 滑翔增程弹弹道优化设计研究[J].四川兵工学报,2013,34(11):8-10.
[10] 张鼎逆,刘毅. 基于改进遗传算法和序列二次 规划的再入轨迹优化[J]. 浙江大学学报,2014,48(1):161-167.
[11] 雍恩米,唐国金,陈磊. 基于Gauss伪普方法的高超声速飞行器再入轨迹快速优化[J].宇航学报,2008,29(6):1766-1771.
[12] Jiang Z, Rui Z. Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J]. Chinese Journal of Aeronautics, 2013, 26(6): 1544-1553.
[13] Jorris T R, Cobb R G. Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 551-572.
[14] Jorris T R. Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints[D]. Ohio, USA: Air Force Institute of Technology, 2007.
[15] Hu Z D. Research on trajectory planning and guidance for space-based strike weapon[D]. Changsha, China: Graduate School of National University of Defense Technology, 2009.
[16] Vinh N X. Optimal trajectories in atmospheric flight[D]. New York:Elsevier Scientific Publishing Company,1981.
[17] 孙勇,段广仁,张卯瑞,等. 高超声速飞行器再入过程改进气动系数模型[J]. 系统工程与电子技术,2011,33(1):134-137.
[18] Benson D A, Huntington G T, Thorvaldsen T P, et al. Direct trajectory optimization and costate estimation via an orthogonal collocation method[J]. Journal of Guidance, Control, and Dynamics, 2006,29(6): 1435-1440.
[19] Huntington G T. Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D]. Cambridge, United States: Massachusetts Institute of Technology, 2007.
[20] Liu Y, Qian Y J, Li J Q, et al. Mars exploring trajectory optimization using gauss pseudo-spectral method[C]//Proc. of the International Conference on Mechatronics and Automation.2012: 2371-2377.
[21] Yong E M, Chen L, Tang G J. Trajectory optimization of hypersonic gliding reentry vehicle based on the physical programming[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5):1092-1097.
[22] 谢富强,吴浩,唐灵灵. 基于粒子群算法的飞行器再入轨迹优化[J].计算技术与自动化,2008,27(4):72-75.
(编辑:薛永利)
Trajectory rapid optimization for reentry hypersonic glide vehicle satisfying complex constraints
WANG Lu,XING Qing-hua,MAO Yi-fan
(School of Air and Missile Defense, Air Force Engineering University, Xi'an 710051, China)
As a typical representation of direct method, in dealing with reentry hypersonic glide vehicle trajectory optimization problem under complex constraints including waypoint or no-fly zone constraints, gauss pseudo-spectral method (GPM) can merely ensure that all the constraints can be satisfied strictly at each Legendre-Gauss (LG) node, but cannot ensure the feasibility of the trajectory between each two neighbor nodes. To overcome this problem, an improved multi-segment gauss pseudo-spectral method was proposed. In this method, first of all, the trajectory was divided into multiple segments by two kinds of proposed nodes, fixed node and virtual node, the first one is used to ensure that each waypoint locates at one of LG nodes, and the second one is used to ensure that there will be more LG nodes locating near the no-fly zones, such that all constraints for whole trajectory can be satisfied; then the number of LG nodes for each segment was given; finally, the sequential quadratic programming method was used to solve the model. Simulation results demonstrate that the proposed optimization method can rapidly generate a reentry trajectory satisfying complex constraints.
reentry hypersonic glide vehicle;trajectory optimization;waypoint;no-fly zone;gauss pseudospectral method
2015-07-18;
2015-09-02。
国家自然科学基金(61272011);全军军事类研究生资助课题(2014JY526)。
王路(1987—),男,博士生,研究方向为地基反临近空间飞行器指挥决策问题。E-mail:408191081@qq.com
V448.2
A
1006-2793(2016)06-0839-08
10.7673/j.issn.1006-2793.2016.06.018
