一种改进S变换的微电网谐波/间谐波检测方法

龚仁喜，刘 畅，周东来

(广西大学电气工程学院， 广西南宁530004)

一种改进S变换的微电网谐波/间谐波检测方法

龚仁喜，刘 畅，周东来

(广西大学电气工程学院， 广西南宁530004)

为了快速、准确地检测出微电网中的谐波/间谐波，以便采取措施对其治理，减小其危害，文中提出了一种改进S变换的谐波/间谐波检测方法。该方法是在S变换的高斯窗函数中引入参数q，并对谐波/简谐波的信号进行S变换，得到含参数q的时频二维复矩阵，取其幅值矩阵中每一个时间采样点最大幅值构成信号随频率变化的最大频谱幅值曲线，则曲线上峰值点的个数即为谐波种类数，峰值点对应的频率即为谐波频率。通过采用最小二乘法计算出实际值与理论值的最小误差可确定参数q的最优取值范围，将该q值作为最终高斯窗指数中引入的q值即得到改进S变换。将改进S变换用于谐波、间谐波检测，并与原始S变换的结果进行了比较，结果表明，改进S变换能够准确获取谐波/间谐波的幅频信息，具有检测精度高、适应能力强、抗噪声性能好等优点。

改进S变换；高斯窗；谐波/间谐波；检测

随着社会和经济的发展，人类对能源的需求不断增长，与此同时，人类生存的环境问题也日益突出。在这种能源需求与环境保护的双重压力下，各国政府都把节约能源、提高能源利用率、发展新能源、加强可再生能源的利用及相关技术的研究研发作为解决这一日益凸显的矛盾的优先考虑方向和重大战略。在这样的背景下，分布式发电(DG)[1]与微电网(MG)的概念被提出，并迅速成为人们关注的焦点和研究的热点。分布式发电是指利用各种分散存在的能源，包括可再生能源(如太阳能、风能、水能等)和本地可方便获取的化石类燃料(如天然气、柴油、煤制气等)获取电能的一种发电形式。微电网是由分布式电源(又称作微电源,如微型燃气轮机MT、风力发电WG、光伏发电PV和燃料电池Fuel等)、储能装置、能量转换装置、相关负荷以及监控和保护装置汇集而成的小型发配电系统，具有环保效益显著、供电可靠性好、发电方式和安装地点灵活等一系列优点。然而，与大电网相比，微电网的容量小、惯性小、抵御外界和内部冲击的能力低，其中，分布式电源和负载具有随机性、间歇性、扰动性、冲击性和非线性的特点，极易引起谐波和间谐波，这将极大地降低电网的电能品质，同时也将严重地威胁供电系统的安全稳定运行[2]，只有快速、准确地检测出这些谐波，才能采取有针对性的措施对其进行有效的控制和治理，确保系统的安全稳定运行。

目前，应用较为广泛的谐波检测方法有短时傅里叶变换[3-4]、小波变换[5-6]和S变换[7-8]。短时傅里叶变换的窗函数固定不变，而小波变换受噪声的影响比较大，对于复杂谐波信号的检测具有一定的限制。S变换[9-10]虽然结合了上述两种方法的优点，解决了分辨率单一的问题，但不适合直接应用在谐波检测中。为了达到精确检测的目的，文献[11]提出一种基于广义双曲S变换的快速谐波检测算法，通过提取复数矩阵中的特征量来确定谐波的幅值、相位等信息，但文中对于复杂谐波并没有深入研究。

本文针对现有的谐波/间谐波检测方法存在的缺陷，提出了一种改进的S变换检测方法，并将该方法应用于谐波/间谐波检测中，旨在提高谐波检测的精确度。

1 改进S变换

信号x(t)的S变换定义为[12]:

(1)

(2)

其中，参数f是频率，t是时间，τ是控制高斯窗在时间轴上的位置的参数。w(τ-t,f)是S变换的高斯窗，其宽度与频率互为倒数[13]。在高斯窗中引进参数q，通过调整高斯窗的形状来提高时频分辨率。改进后的高斯窗为：

(3)

对改进后的高斯窗进行离散化处理，得到：

(4)

式中，N代表采样数，T代表采样间隔，n代表频率采样点，j代表时间采样点。离散信号的改进S变换结果是一个复时频矩阵，该矩阵中的某一行对应频率采样点，某一列对应时间采样点，求模后的矩阵即为改进S变换的模矩阵。其中，列向量表示某一时刻随频率变化的分布，行向量表示某一频率随时间变化的分布。因此，矩阵中某一位置的元素表示了相应频率和时间处信号的改进S变换幅值。

2 检测原理

①次数检测

信号的改进S变换可以表示成：

MST(τ,f)=A(τ,f)ejφ(τ,f)。

(5)

利用幅值矩阵A(τ,f)中采样点对应的最大值组成的向量得到最大频谱曲线，该曲线上有多少峰值点就表示有几种谐波，每一个峰值点对应的频率即为谐波的频率。

②幅值检测

幅值计算公式为：

(6)

式中，u0为基波电压，A0、Ak分别表示基波幅值和谐波幅值。

3 参数优化

改进S变换和S变换反映的都是被测信号x(t)在时刻τ和频率f时刻的成分，变换后的模矩阵中，列向量和行向量分别表示某时刻随频率的变化分布和某频率随时间的变化分布，矩阵的某一元素即为相应频率和时间对应的信号幅值。因此，本研究将选取不同q值对谐波间谐波进行检测，然后根据最小二乘法计算出理论值与实际值的最小误差，确定q值的范围。设被测信号为：

(7)

其中，A=0.38，B=C=0.3，D=0.2，E=0.5，F=0.38。表1为被测信号的理论值和选取不同q值(1.0,0.6,0.4,0.3,0.2,0.1,0.05,0.04,0.01)时检测后的实际值。

表1 信号理论值和不同q值的检测结果
Tab.1 Signal theory value and detection results for differentq

频率/Hz理论幅值/V检测幅值/V100604030201005004001120118214541302122511901184118211821182118215093314741251109810189569349339339332309331035952936934933933933933933350622103774865363062362262262262245015562532221219681820166915661556155615565201182234820581822165214421226118311821182

表1中给出了被测信号中各个频率的理论值和选取不同q值的检测结果，可见，当1.0≤q≤0.05时，检测到的频率幅值均与理论值有偏差。随着q值减小到0.04时，频率与幅值的实际值与理论值相同。根据表1的数据，利用式(7)求得理论幅值Y1i与实际幅值Y2i之间的最小平方和误差e为：

(8)

其中，n=6(被测频率点数)，i=1,2,3,…,6。

表2 不同q值的最小误差e
Tab.2 Minimum error for differentq

q值10604030201005004001误差e2860661329186092229788808920400100

表2为取不同q值时的幅值最小误差，当0.04≤q<0时，检测结果误差e为0。因此，本研究将选取q=0.02对不同信号进行仿真实验，与S变换进行对比，以说明改进算法的正确性。

4 仿真对比

4.1 间谐波信号仿真结果

设间谐波信号为：

(9)

其中，A=0.23，B=0.38，C=0.3，D=0.09，E=0.38。图1(a)和图1(b)分别为改进的S变换和S变换对间谐波信号的检测结果。图1(a)的改进S变换幅频曲线中包含有基波和0.5、2.4、4.6、7.4、10.4次谐波，其对应的峰值分别为311.1、71.6、118.2、93.3、28.0、118.2 V，每一峰值点的频率幅值均与理论值相同。图1(b)中包含25、50、120、230、520 Hz的峰值点，但并没有检测出370 Hz的间谐波峰值点，且各个频率点幅值均有误差。以上结果表明，改进的S变换对于间谐波检测的准确率高。

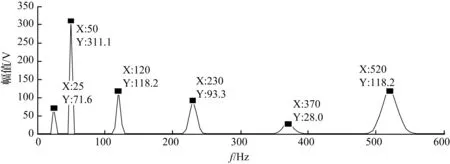
(a) 改进S变换幅频曲线

(b) S变换幅频曲线

表3是被测信号理论值与S变换、改进S变换检测后的频率、幅值比较。通过对比发现，改进后的S变换检测误差为零，能够准确获得所有频率点的频率和幅值。而S变换的检测结果与理论值均有差别，不适合直接应用在间谐波检测中。

表3 间谐波检测结果对比
Tab.3 Comparison of detection results of inter-harmonics

指标各频率间谐波幅值/V基波25120230370520理论值311171611829332801182改进S变换311171611829322801182S变换311671611869473821238

4.2 谐波信号仿真结果

设谐波信号为：

(10)

其中，A=0.6，B=0.5，C=0.4，D=0.3，E=0.2。图2(a)和图2(b)分别为改进S变换和S变换对谐波信号检测后的幅频曲线。由图2(a)中可以清晰观察到3、5、7、9、11次谐波，其对应的峰值分别为186.7、155.6、124.5、93.3、62.2 V，与理论幅值相同，而图2(b)中的检测结果中明显看到只检测到了3个频率点。上述结果说明，改进的S变换对于谐波检测的准确率很高。

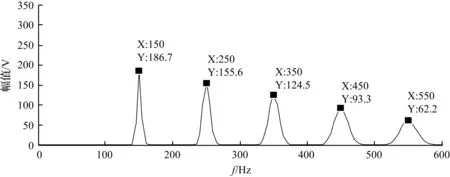
(a) 改进S变换幅频曲线

(b) S变换幅频曲线

表4是原始S算法、改进S变换与实际输入信号的频率、幅值对比。从表4中可以看到，改进后的检测误差为零，准确获得所有频率点的频率和幅值。

表4 谐波检测结果对比
Tab.4 Comparisonof detection results of harmonic

指标各频率间谐波幅值/V150250350450550理论值186715561245933622改进S变换186715561245933622S变换18671688174116691204

4.3 噪声影响分析

给式(9)中的稳态间谐波信号中分别加入噪声比为40、60 dB的高斯白噪声，则给出SNR为40 dB的检测波形，如图3所示。图4是三维幅度—时间—频率曲线。从图3中可以清晰观察到信号的频率分布。表5为理论值和两种不同信噪比的误差值，结果表明，信噪比越大，误差越小，改进算法在噪声环境中得到的波形与非噪声环境下的结果相似，说明改进算法对于含噪声的间谐波信号检测具有明显的抑制作用，保证了在噪声情况下检测的准确率。

(a) 含40 dB噪声的间谐波信号

(b) 含40 dB噪声的最大频率幅值曲线

图4 含噪声的间谐波的幅度—时间—频率变化曲线Fig.4 The variation curve of amplitude-time-frequency with noise

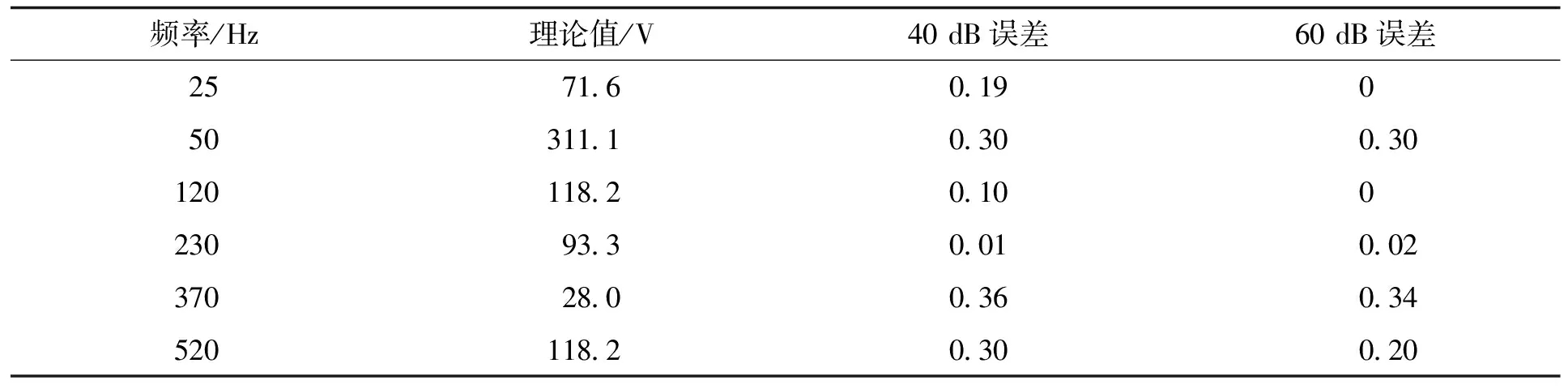
频率/Hz理论值/V40dB误差60dB误差257160190503111030030120118201002309330010023702800360345201182030020

5 结 语

本文提出了一种改进的S变换谐波/间谐波检测方法。首先对S变换进行改进,即在原始S变换的高斯窗函数中引入参数q，利用最小二乘法计算出实际值与理论值的最小误差，并对引入的参数进行优化。然后将改进后的算法应用在谐波/间谐波检测中。对比改进的S变换和S变换的仿真结果可见，改进后的S变换应用于谐波、间谐波和复杂谐波的检测中具有很高的检测精度，而原始S变换的检测结果与理论值相比存在较大误差，无法准确获取信号中各个频率点，表明原始S变换不适合直接应用在谐波检测中。另外，噪声仿真分析表明，改进的S变换方法还具有良好的抗噪声能力。

[1] 唐文强,吕智林,胡立坤.直流微电网孤立运行控制策略研究[J]. 广西大学学报(自然科学版), 2014,40(5):1027-1033.

[2] 龚仁喜, 刘丰, 黄阳.一种基于FPGA+ARM的高速电力谐波检测仪硬件的设计与实现[J]. 广西大学学报(自然科学版), 2009, 34(1):92-96.

[3] 张伏生,耿中行,葛耀中.电力系统谐波分析的高精度FFT算法[J]. 中国电机工程学报, 1999, 19(3):63-66.

[4] FERRERO A, OTTOBONI R.High accuracy fourier analysis based on synchronous sampling techniques[J]. IEEE Transactions on Instrumentation and Measurement, 1992, 41(6):524-527.

[5] 房国志,杨才山,杨超.基于Meyer小波和FFT的电网间谐波检测[J]. 电力系统保护与控制, 2011, 39(12):90-93.

[6] 曾瑞江,杨震斌,柳慧超.基于小波变换的电力系统谐波检测方法研究[J]. 电力系统保护与控制, 2012, 40(15):35-39.

[7] SAMANTARAY S R, PANIGRAHI K B, DASH P K, et al.Power transformer protection using s-transform with complex window and pattern recognition approach[J]. Generation Transmission & Distribution, 2007,1(2):278-286.

[8] YI J, PENG J, LUO A.Power quality signal denoising using modified S-transform[J]. Chinese Journal of Scientific Instrument, 2010, 31(1):52-58.

[9] VENTOSA S, SIMON C, SCHIMMEL M,et al.The s-transform from a wavelet point of view[J]. IEEE Transactions on Signal Processing,2008,56(1):2771-2780.

[10]STOCKWELL R G, MANSINHA L, LOWE R P.Localization of the complex spectrum: the s transform[J]. IEEE Transactions on Signal Processing,1996,44(4):998-1001.

[11]郑曙光,刘观起.基于广义双曲S变换的快速谐波检测算法[J]. 电测与仪表, 2015, 52(9):30-35.

[12]易吉良,彭建春,罗安.电能质量信号的改进S变换降噪方法[J]. 仪器仪表学报, 2010, 31(1):32-37.

[13]易吉良,彭建春,谭会生.S变换在电能质量扰动分析中的应用综述[J]. 电力系统保护与控制, 2011, 39(3):141-147.

[14]肖助力,龚仁喜,陈双.基于改进S变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2015, 43(3):84-90.

(责任编辑 裴润梅)

An improved S-transform method for detecting harmonics/inter-harmonics in micro-grid

GONG Ren-xi， LIU Chang， ZHOU Dong-lai

(College of Electrical Engineering, Guangxi University, Nanning 530004, China)

In order to detect the harmonics/inter-harmonics in the micro-grid quickly and accurately so as to take measure to treat them and to reduce their harmfulness to the power system, an improved S-transform method for detecting harmonics/inter-harmonics in micro-grid is proposed. Firstly, a parameterqis introduced into the Gaussian window function in S-transform. Then S-transform is carried out for any signal with harmonics/ inter-harmonics to obtain a two-dimensional complex amplitude-frequency matrix withq. The maximum amplitude frequency curve is constituted by taking its maximum amplitude in the amplitude matrix at each time sampling point. Then the number of the peak points is the very harmonic type number, and the responding frequency to the each peak point is just the harmonic frequency. The least error between the actual values and the theoretical values can be calculated out and the optimal value range ofqcan be determined by utilizing the least square method, and the q-value functions as the finalqvalue in Gaussian window exponent, thus obtaining the improved S-transform. Finally, a utilization of the improved S-transform for detecting the harmonics/ inter-harmonics is made and a comparison of the results based on S-transform and improved S-transform is performed. From the comparison results, the improved S transform can obtain the amplitude-frequency information of harmonics/inter harmonics accurately. The results show that the improved S-transform has the advantages of high detection precision, strong adaptability and good anti-noise performance.

improved S-transform; gaussian window; harmonics and inter-harmonics; detection

2016-05-10；

2016-06-01

国家自然科学基金资助项目(61561007)

龚仁喜(1962—)，男，广西桂林人，广西大学教授，博士，博士生导师；E-mail：rxgong@gxu.edu.cn。

龚仁喜，刘畅，周东来.一种改进S变换的微电网谐波/间谐波检测方法[J].广西大学学报(自然科学版)，2016，41(6)：1839-1846.

10.13624/j.cnki.issn.1001-7445.2016.1839

TM714

A

1001-7445(2016)06-1839-08