水平对数周期天线振子杆裹冰模拟试验

宋宗凤，郭伟，王佐祥，鲁 赛

(中国电波传播研究所， 山东青岛266107)

水平对数周期天线振子杆裹冰模拟试验

宋宗凤，郭伟，王佐祥，鲁 赛

(中国电波传播研究所， 山东青岛266107)

为研究水平对数周期天线振子杆的抗裹冰能力，以某地区天线的振子杆为研究对像，进行了裹冰模拟试验和仿真分析。结果表明，改进设计后振子杆无损坏，可满足重裹冰区的裹冰要求。试验数据同时还验证了理论分析结果的可使用性，两者的变化趋势一致，振子杆最大节点位移出现在工况二下第4节末端为347.55 mm，与仿真结果相对误差为5.87%。表明在条件不允许做试验的情况下，可通过仿真代替试验指导设计，该方法方便快捷经济。

水平对数周期天线；振子杆；裹冰；模拟试验；有限元软件ANSYS

0 引 言

随着气候的变化，裹冰日趋成为一种普遍的严重的自然灾害。2008年，南方某些省区遭受了近50年以来范围最大、时间最长、冰冻雨雪最为严重的灾害天气，以致这些地区的部分输电线路出现倒杆/塔及线路断线的现象，导致南方地区大面积出现断电情况。这些灾害给国民经济带来了巨大的经济损失和人民生活的极大不便[1-2]。

近年来，关于裹冰方面已有一些研究成果，如文献[2-3]对输电线的覆冰形成原因及覆冰机理进行了详细的分析；文献[4]对裹冰和风荷载作用下的南方某输电铁塔的可靠度进行了分析；文献[5]主要通过建立一种简单的模型对冻雨冰荷载进行了研究；文献[6-7]主要对电网系统裹冰和融冰技术和方法进行了研究；文献[8-10]对架空导线的裹冰状况自动检测进行了研究。文献[11]以南方某失事输电塔为例，采用有限元分析软件ANSYS，建立了输电塔及导线的模型，对多种情况下所引起的结构变形作了比较；文献[12]通过对输电线路裹冰的形成、表现形式及其危害的分析研究，提出了可采取的防范、治理措施，以逐步减少输电线路裹冰事故的发生。

以往研究主要是对裹冰成因、检测、除冰、防范治理等进行了理论分析和研究，并未对具体结构的抗裹冰能力进行试验分析和验证。由于某地区属于北方小区域特殊的恶劣气象条件，2014年初又出现了超常极端的雨雪天气，架设在该地区的水平对数周期天线振子杆出现了弯折现象。因此，为了保证对数周期天线结构在冰冻雨雪等恶劣气候环境条件下的正常运行，研究对数周期天线结构在不同冰冻荷载作用下的安全性、可靠性，具有重要的工程实用价值。

本文以水平对数周期天线振子杆为研究对象，对优化设计后的振子杆进行裹冰模拟试验，并以试验条件为已知参数，在有限元软件ANSYS[13]平台上，对振子杆进行了详细的裹冰仿真分析。试验数据和仿真数据均表明，改进设计的振子杆无损坏，可满足重裹冰区的裹冰要求。

1 荷载模型

1.1 裹冰荷载

裹冰荷载除了与裹冰厚度有关外，还与形式有关，一般有全裹冰和部分裹冰形式。由于实际情况极为复杂，裹冰形式亦是各式各样的。实际分析时，通常按全裹冰和上半裹冰两种情况考虑，视哪种形式对结构受力不利而定，本文中按全裹冰情况分析。

全裹冰时的裹冰荷载分圆截面和非圆截面两种构件[14]，本文构件主要为圆截面构件，下面主要介绍圆截面构件的裹冰荷载计算方法。

圆截面的构件、拉绳、缆索、架空线等，每单位长度上的裹冰荷载为：

q1=πba1a2(d+ba1a2)γ×10-6(kN/m)，

(1)

式中，q1为裹冰荷载，kN/m;b为基本裹冰厚度，mm；d为圆截面的构件、拉绳、缆索、架空线的直径，mm；γ为裹冰重度，在此取7 kN/m3(实际裹冰类型为混合淞)；a1为裹冰厚度直径修正系数，如表1所示；a2为高度递增系数，如表2所示。

表1 裹冰厚度的直径修正系数a1
Tab.1 Diameter correction factor of wrapped ice thicknessa1

直径/mm510203040506070a1110100090080075070065060

表2 裹冰厚度的高度递增系数a2
Tab.2 Height incremental coefficient of wrapped ice thicknessa2

离地面高度/m1050100150200250300≥350a21016202224252728

1.2 风荷载

天线在使用时，风荷载的作用影响较大，故风荷载应作为主要外荷载被考虑。荷载的大小根据GB50135-2006 《高耸结构设计规范》[14]中4.2节确定。

基本风压可按下式计算:

ω0=v2/16。

(2)

1.2.1 杆塔风荷载计算

垂直作用于高耸结构表面单位面积上的风荷载标准值按下面公式计算：

ωk=βzμsμzω0，

(3)

式中,ωk为作用在高耸结构z高度处单位投影面积上的风荷载标准值(kN/m2，按风向投影)；ω0为基本风压，kN/m2，其取值不得小于0.35 kN/m2；μz为z高度处的风压高度变化系数；μs为风荷载体型系数；βz为z高度处的风振系数。

根据文献[14]中表4.2.6-1和表4.2.7分别确定μz和μs，βz则根据4.2.9节确定，经计算得到风荷载标准值ωk。ωk乘以天线结构的受风投影面积即可得到天线结构的压力值，然后按照静力荷载作用平均分配到模型中对应结构的每个节点上，即可完成对模型中天线结构荷载的确定。

1.2.2 柔索风荷载计算

垂直作用于柔索表面单位面积上的风荷载标准值按下面公式计算：

ωx=αω0μzμscβcsinθ2，

(4)

式中，ωx为垂直于柔索方向的水平荷载标准值(kN/m2，按风向投影)；α为风压不均匀系数；μsc为柔索的体型系数；βc为风荷载调整系数；θ为风向与柔索方向之间的夹角(°)。

1.3 荷载等效

根据1.1和1.2节中公式(1)～(4)及表1和表2，可以计算出振子拉线和每段振子杆裹冰荷载及风荷载。为了加载方便，在此假设风荷载方向与自重同向。通过在振子拉线和振子杆上等间距悬挂等荷载的绝缘子来等效模拟裹冰荷载和风荷载。

等效集中荷载数量为奇数时的弯矩等效公式为：

(5)

式中，q为计算出的风荷载和裹冰荷载(N/m)；l为两支点跨距；g为等效的单个集中荷载值；n为等效集中荷载数量。

等效集中荷载数量为偶数时的弯矩等效公式为：

(6)

2 试验过程

2.1 试验条件

对振子两种工况进行了试验，两种工况的具体内容如下：

①工况一：振子杆及振子拉线裹冰和振子杆受风载加载试验，裹冰条件为振子杆裹冰厚度10 mm、拉线裹冰厚度30.5 mm、振子杆基本风压0.15 kN/m2；

②工况二：振子杆、振子拉线均受裹冰和风载加载试验，裹冰条件为振子裹冰厚度10 mm、拉线裹冰厚度30.5 mm、振子杆及振子拉线基本风压0.15 kN/m2。

2.2 振子杆安装

由于理论计算过程中，振子杆根部和振子拉线端点的固定位置为全约束点，而实际上被测试振子安装在试验场内的1 000 mm边宽的钢管塔上，被测试振子安装图如图1所示。固定振子用长度为4 400 mm的槽钢，槽钢中间位置使用U型抱箍固定在钢管塔的铁塔主柱上。

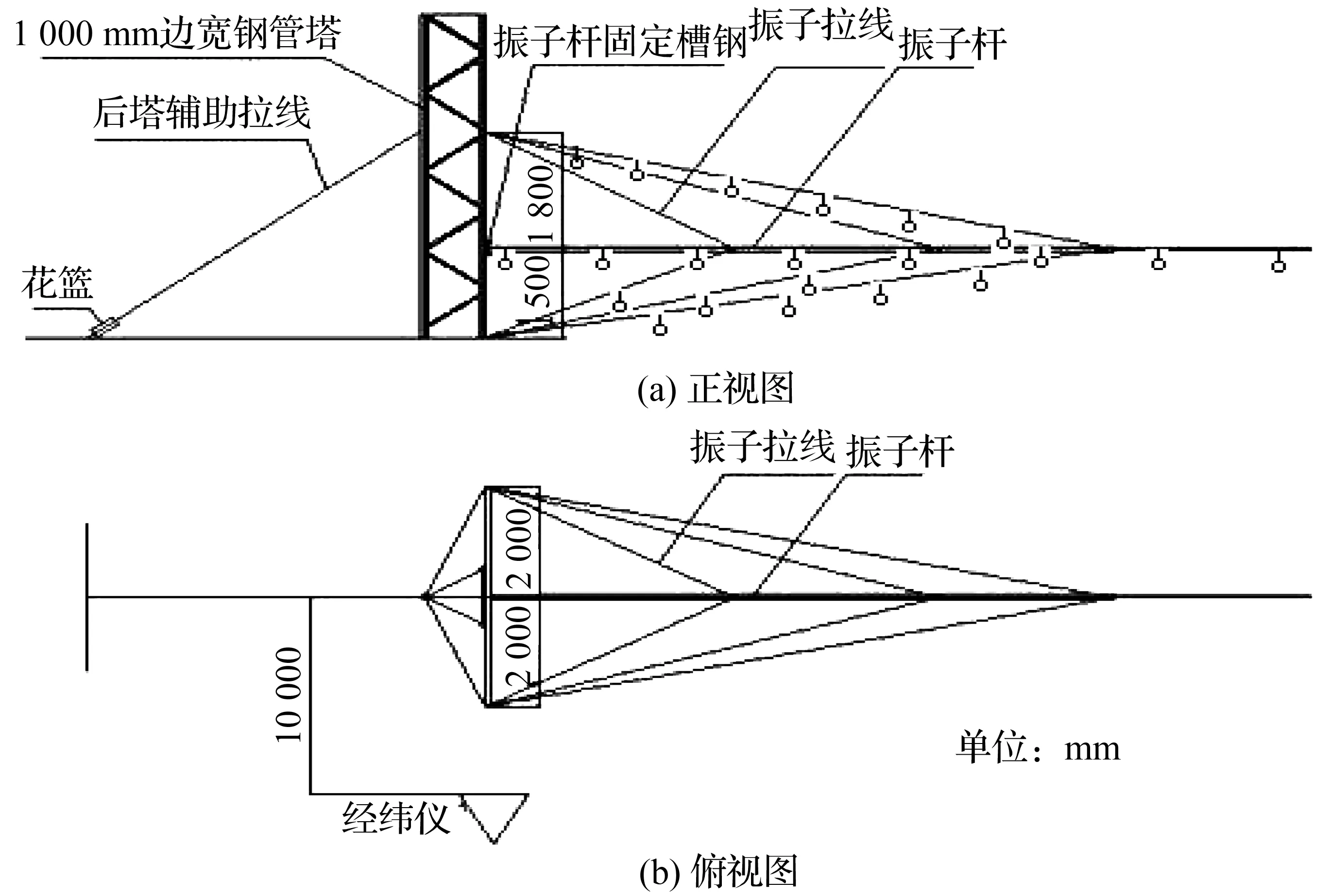
图1 被测试振子杆安装图Fig.1 Installation diagram of oscillating rod to be tested

2.3 加载过程

试验振子总长约12.3 m，由四种规格变截面铝管组成。

在工况一情况下，振子杆加载的负载重量为79.2 kg，振子拉线加载的负载重量为198.4 kg，总加载负载重量为277.6 kg。试验前先将用来加载的每个绝缘子称重并贴标签，然后根据要求间距在振子拉线和振子杆上画线，加载时要求两边对称悬挂绝缘子，图2(a)为工况一加载完成图。

在工况二情况下，振子杆加载的负载重量为79.2 kg，振子拉线加载的负载重量为252.5 kg，总加载负载重量为331.7 kg。图2(b)为工况二加载完成图。

(a) 工况一

(b) 工况二

图2 工况一和工况二时振子杆及拉线加载完成图
Fig.2 Load pictures of oscillating rod and cable under two conditions

3 试验结果分析

3.1 仿真分析结果

根据裹冰试验加载数据，在有限元软件ANSYS平台上，对振子杆进行了详细的裹冰仿真分析。图3(a)和(b)分别为工况一和工况二下振子节点位移云图。从图3(a)中知工况一下振子杆最大节点位移为291 mm，从图3(b)中知工况二下振子杆最大节点位移为327 mm，均出现在振子杆自由端。

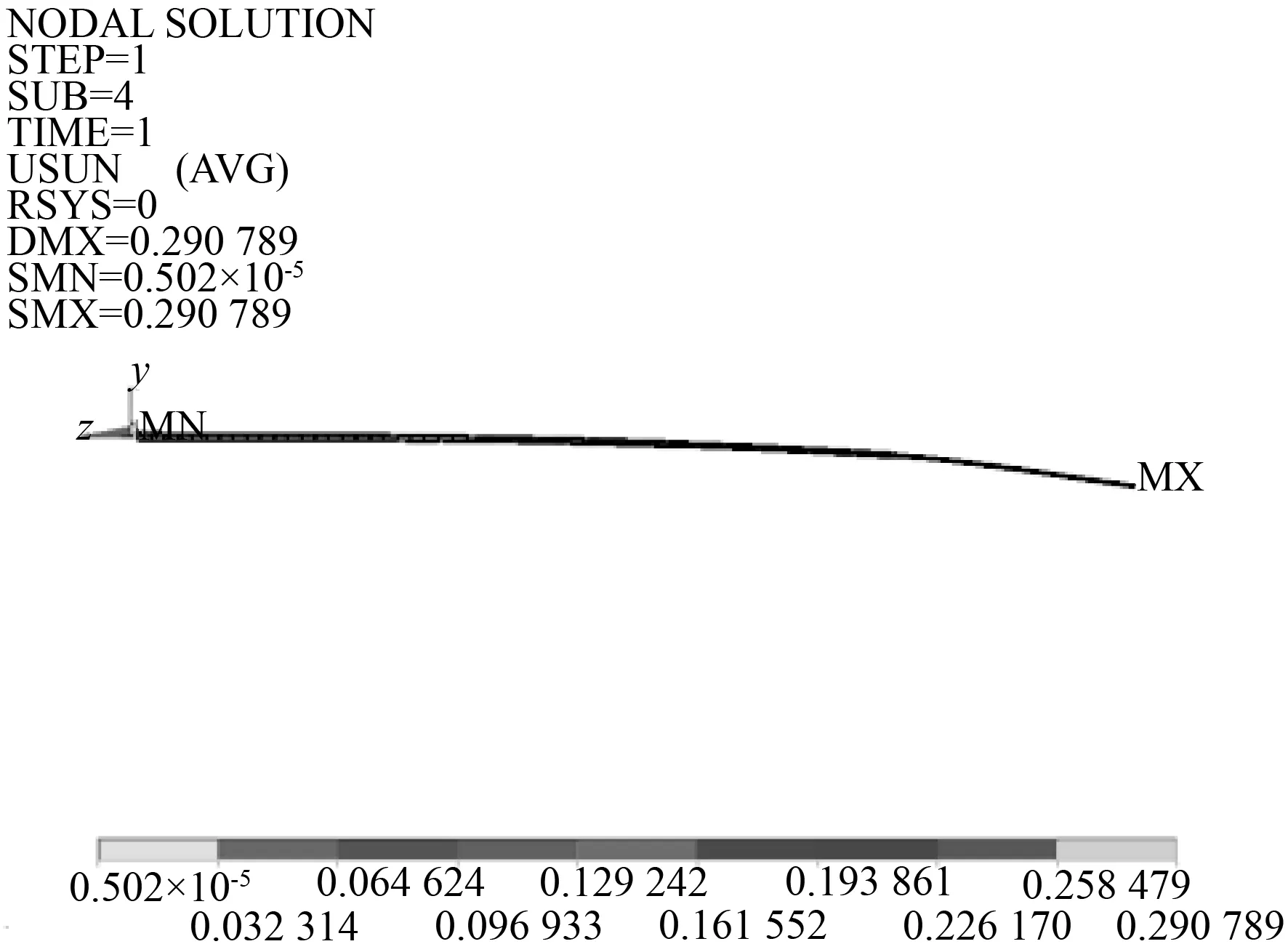
(a) 工况一

(b) 工况二

图3 工况一和工况二下振子节点位移云图
Fig.3 Nodal displacement of oscillating rod under two conditions

3.2 试验数据的处理与分析

试验选用的振子杆每节接头之间存在一定的间隙，该间隙引起每节振子端部产生一定的位移量，从而影响到振子杆的整体位移。通过实测每节振子结构之间的间隙推导出振子杆的位移，去除其影响的数据，详细数值见表3、表4、表5。

表3 测量铝管的数值
Tab.3 Measured values of tubes

序号名称长度/mm测量直径值/mm间隙/mm1连接底座 0869002第一节接头1370087160263第一节接头23700789004第二节接头1305079520625第二节接头23050688606第三节接头1260369560707第三节接头22603451008第四节接头29524486-024

表3中列出了由于各节铝管振子之间的间隙，第一节和第二节连接处的间隙最大为0.62 mm。

表4 振子接头间隙引起位移值
Tab.4 Displacement value caused by the oscillating joint gap mm

接头长度振子分段长分段间隙引起位移间隙引起每节振子末端位移140370068768714030501351203814026031302333914029525063845

表4中列出了由于振子杆接头间隙引起的各节振子末端位移值，振子杆自由端位移值最大为38.45 mm。

表5 间隙引起位移值Tab.5 Displacement value caused by the gap mm

表5中列出了处理过后的振子杆各节末端的位移值，最大值为33.39 mm。

根据试验对象及试验加载情况，对试验对象在有限元软件ANSYS平台上进行建模，对振子杆、振子拉线的两种工况进行仿真分析，具体仿真结果见3.1节。对试验结果和仿真结果进行比较，试验处理的数据见表6。相对误差值计算方式如下：

相对误差值(%)=(试验测量值-仿真值)/试验测量值×100。

表6 间隙引起位移处理后的数据
Tab.6 Displacement value caused by the gap

名称位移第2节末端第3节末端第4节末端工况一试验/mm53621216129155仿真/mm46741110329063相对误差/%1284870031工况二试验/mm68621616134755仿真/mm53231310632715相对误差/%22441890587

表6中分别列出了工况一和工况二下振子杆各节末端试验和仿真位移值以及两者的相对误差。从表6中可以看出：

①工况一，振子的位移相对误差最大出现在第2节末端为12.84%，最小出现在第4节末端为0.31%；

②工况二，振子的位移相对误差最大出现在第2节末端为22.44%，最小出现在第4节末端为5.87%。

经分析，引起振子杆各节末端试验和仿真位移误差的原因如下：

①每节振子之间装配存在一定的间隙；

②拉线理论伸长量与实际伸长量存在一定的误差；

③安装误差，振子初始状态与仿真模型初始状态存在差异；

④测量误差，试验过程中测量振子位移及振子拉线拉力存在一定的误差；

⑤施加荷载，由于试验时施加的外荷载数量较多，且每个重量存在微差，仿真时将外荷载简单处理成平均重量施加在相应节点上所造成的。

综合考虑振子杆的两种荷载工况，通过以上数据及分析结果，得出试验数据均较仿真数据大，但试验与仿真位移趋势是一致的，表明本文试验方法和仿真的正确性。经过误差分析得出试验数据偏大是由于振子管连接之间的间隙、安装以及测量误差引起的。同时考虑到试验既费时、费力，又费钱，因此建议以后遇到技术要求提出裹冰要求的，可通过理论仿真对结构进行前期计算(仿真时可将设计余量相应增大)以指导结构设计，在时间、费用允许的条件下可再进行相关试验验证。

4 结 论

在最恶劣的工况二情况下，振子杆最大节点位移为347.55 mm(与仿真结果相对误差为5.87%)，且振子并未出现损坏，故优化后的振子杆可以承受该工况载荷，可满足振子杆强度要求。

在试验过程中，由于条件限制无法测量各个节点的应力，只能测量振子各节点位移量。但由于多种原因，例如：测量误差、振子杆连接处的间隙、不锈钢丝绳拉线伸长量等因素，引起了实际测量值与理论计算值差别，但其变形趋势是一致的，并且其影响在合理的范围之内，该测量数据真实可靠。该试验过程具有相当重要的研究价值，为进一步的细化与改进提供了重要的依据。同时验证了理论分析结果的可使用性，若在条件不允许做试验的情况下，可通过理论仿真来代替试验来指导设计，该方法方便快捷，且经济实用。

[1] 蒋兴良,易辉.输电线路裹冰及防护[M]. 北京:中国电力出版社, 2002：1-9.

[2] 陈百炼,吴战平,张艳梅,等.贵州冬季电线积冰及其天气成因分析[J]. 气象，2014, 40(3):355-363.

[3] 刘春城,刘佼.输电线路导线覆冰机理及雨淞覆冰模型[J]. 高电压技术，2011, 37 (1):241-248.

[4] 铁华,侯建国,安旭文.裹冰、风荷载作用下南方某输电铁塔可靠度分析[J]. 武汉大学学报(工学版), 2011, 44(2):207-210.

[5] JONES K F. A simple model for freezing rain ice loads[J]. Atmospheric Research, 1998, 46(1): 87-97.

[6] 王治,李少华.架空输电线路覆冰和融冰仿真研究[J]. 科技情报开发与经济, 2011, 21(36):139-142.

[7] LAFORTE J L, ALLAIRE M A, LAFLAMME J.State-of-the-art on power line deicing[J]. Atmospheric Research, 1998, 46(1): 143-158.

[8] MASOUD F, KONSTANTIN S.Statistical analysis of field data for precipitation icing accretion on overhead power lines[J]. IEEE Transactions on Power Delivery, 2005, 20(2):1080-1087.

[9] 侯慧,吕泽焱, 董朝阳,等.基于实时图像及灰色预测的输电线覆冰灾害预警[J]. 武汉大学学报(工学版), 2015, 48(5): 697-700.

[10]周封,刘闻博,刘志刚,等.智能视频技术在电力系统领域的应用[J]. 哈尔滨理工大学学报, 2015, 20(5):14-19.

[11]罗靓,刘本玉.冻灾中南方输电塔失事的分析[J]. 云南大学学报(自然科学版)，2008, 30(S2):282-285.

[12]魏长喜.110kV线路裹冰防范措施及对策[J]. 四川电力技术, 2010, 33(3):30-32.

[13]龚曙光,黄云清.有限元分析与ANSYS APDL 编程及高级应用[M]. 北京:机械工业出版社, 2009：76-133.

[14]上海市建设和交通委员会.高耸结构设计规范：GB50135-2006[M]. 北京: 中国计划出版社, 2007：17-37.

(责任编辑 梁 健)

Simulation test of oscillating rod of horizontal logarithm period antenna under wrap ice

SONG Zong-feng，GUO Wei，WANG Zuo-xiang，LU Sai

(China Research Institute of Radio Wave Propagation,Qingdao 266107, China)

To research the level of log-periodic oscillating element rod anti-wrapped ice ability, the simulation test and simulation analysis on the image of the antenna in a certain area was carried out. The analysis results show that the improved design can avoid the damage of oscillating rod, which can meet the requirements of the heavy ice wrapped ice. Experimental data also confirm the theoretical analysis results can be used, both trends are the same. The maximum node displacement of the oscillating rod is 347.55 mm at the end of the 4 section of the second working condition, and the relative error of the simulation results is 5.87%. The above data shows that, instead of the field test, simulation test and analysis can guide the design, which is convenient and economical method.

horizontal log-periodic antenna；oscillating rod；wrap ice；simulation test；finite element software ANSYS

2016-07-12；

2016-08-24

国家自然科学基金资助项目(41175012)

宋宗凤(1982—), 女, 山东莒县人, 中国电波传播研究所高级工程师, 博士后；E-mail: anybody_szf@163.com。

宋宗凤，郭伟，王佐祥，等.水平对数周期天线振子杆裹冰模拟试验[J].广西大学学报(自然科学版)，2016，41(6)：1832-1838.

10.13624/j.cnki.issn.1001-7445.2016.1832

TN821.6

A

1001-7445(2016)06-1832-07