蝴蝶形钢板剪力墙自复位结构有限元分析

2017-01-04李启才

广西大学学报（自然科学版） 2016年6期

关键词：剪力墙抗震蝴蝶

王阳，李启才，王琦，纪瑞

(苏州科技大学江苏省结构工程重点实验室，江苏苏州215011)

蝴蝶形钢板剪力墙自复位结构有限元分析

王阳，李启才，王琦，纪瑞

(苏州科技大学江苏省结构工程重点实验室，江苏苏州215011)

为了明确蝴蝶形钢板剪力墙自复位结构的抗震性能，通过经验证有效的有限元数值模拟方法，比较了不同高厚比的蝴蝶形板在结构滞回性能、单位体积耗能、耗散系数、面外最大位移、面外滞回曲线方面的差异，借助骨架曲线分析了不同高厚比的蝴蝶形钢板剪力墙对结构承载力和延性的影响。结果表明：高厚比为300的蝴蝶形钢板剪力墙自复位结构的综合性能优于其他高厚比的蝴蝶板，建议蝴蝶形板高厚比控制在300左右。最后，还提出残余变形是衡量自复位结构复位性能的重要指标，并初步给出了高厚比最小限值的理论公式。

蝴蝶形钢板;自复位结构;高厚比;滞回耗能;残余变形

Absteact： In order to investigate the seismic performance of self-centering steel frame with infilled butterfly-shaped steel plate walls, the effects of different height to thickness ratios on the hysteretic behavior, the energy dissipation per volume, the dissipation coefficient, the maximum out-of-plane deformation and the out-of-plane hysteresis curve were studied by the finite element method and verified by experiments. Moreover, the horizontal bearing capacity and ductility at different height to thickness ratios were analyzed according to the skeleton curves.The results show that the comprehensive performance of the butterfly-shaped steel wall with height to thickness ratio of 300 is better than that of the others. A height to thickness ratio of 300 is suggested for designation. The residual deformation is put forward as an important index for the reset function of self-centering structure, and the theoretical formula for the minimum value of the height to thickness ratio is given.

0 引言

钢结构在地震作用下通过其自身材料的延性和结构发生变形来耗散地震能量，震后往往产生很大的残余变形，其修复难度大，即使钢结构使用韧性较好的钢材也未必能达到预期的延性效果，原因是在很短的时间内地震作用传递到钢结构上，使钢材性能发生了变化，在结构发生整体屈曲和局部屈曲的地方钢材会因进入塑性发生弱化，而在高应力的地方和缺陷处甚至可能会发生断裂。1994年美国北岭地震和1995年日本兵库地震中曾发生过较严重的局部破坏，震中附近出现了许多梁柱焊接刚性连接破坏的现象，其连接部位破坏十分严重[1]。针对传统结构的不足，蝴蝶形钢板剪力墙自复位结构使用常规材料改良了钢板上开竖缝的技术，形成板条弯曲变形耗能机制，并与梁柱后张法自复位节点技术结合，提高节点的变形能力。这种结构在中震、大震下曾表现出不俗的抗震性能，适用于高烈度区的抗震结构，因此受到诸多学者的关注。

文献[2-4]中提出了基于性能的抗震设计目标：50年内众值烈度的超越概率为63.2%时，内填钢板、框架梁、柱均处于弹性，结构不坏；超越概率为10%时，内填钢板屈服耗能，框架梁、柱处于弹性状态，结构可修；超越概率为2%时，内填钢板变形很大，框架梁、柱出现少量塑性，结构不倒。马磊等[5]运用有限元软件比较了蝴蝶形钢板承载力的理论计算值和有限元计算值，给出了计算蝴蝶形钢板承载力的修正公式。朱昱等[6]对钢板剪力墙自复位结构设计中的钢绞线截面积、初始预拉力、钢板厚度等参数给出定性的分析。本文将采用经验证有效的有限元数值模拟方法，对高厚比这一参数，从结构滞回性能、单位体积耗能、耗散系数、面外最大位移、面外滞回曲线和残余变形等方面进行比较分析，借助骨架曲线分析高厚比对结构承载力和延性的影响，以进一步明确高厚比对蝴蝶形钢板剪力墙自复位结构抗震性能的影响，为高厚比参考设计值的设定提供参考。

1 有限元模拟方法的验证

本研究将对钢板剪力墙结构和自复位节点分别验证。钢板剪力墙模型采用文献[7]中的SPSW-H试件模型。利用有限元软件ANSYS 12.0自顶向下建立模型，框架梁、柱和钢板采用Shell 181单元模拟，钢绞线采用Link 10单元模拟，本构关系为双线性模型，强化模量0.02E，为了真实反映结构的抗震性能，取屈曲模态的千分之一作为初始缺陷，考虑材料非线性和几何非线性，因钢板的求解过程容易出现不收敛的现象，优先考虑FullNewton-Raphson迭代计算方法。编写APDL语言按位移施加循环荷载分析结构的各项性能。试验中液压加载器位于结构的左侧，规定拉向为正，推向为负。试验和有限元计算的滞回曲线如图1所示，当位移加载到+5.8 mm时，试验值和模拟值分别为525.2 kN和536.9 kN；当位移加载到+11.6 mm，试验值和模拟值分别653.4 kN和653.8 kN；当位移加载到+17.4 mm时，试验值和模拟值分别位611.4 kN和613.5 kN，有限元模拟时底部和侧向所加约束是理想状态，实际情况要弱于模拟，因而有限元计算得到的相应荷载值略高，但总体而言，二者吻合较好。

(a) 试验结果

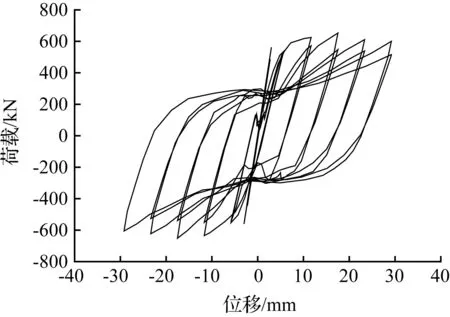
(b) 模拟结果

图1 钢板剪力墙滞回性能验证对比
Fig.1 Hysteresis curve of steel plate shear wall

自复位节点验证采用文献[8]的自复位节点JD2模型，本构关系为双线性模型，强化模量0.02E，考虑材料非线性和几何非线性。图2为自复位节点验证对比结果，可见该自复位节点在循环荷载下的有限元模拟的滞回曲线与试验的滞回曲线差别不大，有限元计算的滞回曲线呈现“双旗帜形”。试验所得曲线的初始刚度比有限元数值模拟略小，原因是有限元数值模拟在角钢处螺栓用耦合的方式简化，实际情况会出现一定的滑移，但有限元数值模拟结果满足精度要求，模拟方法切实可行。

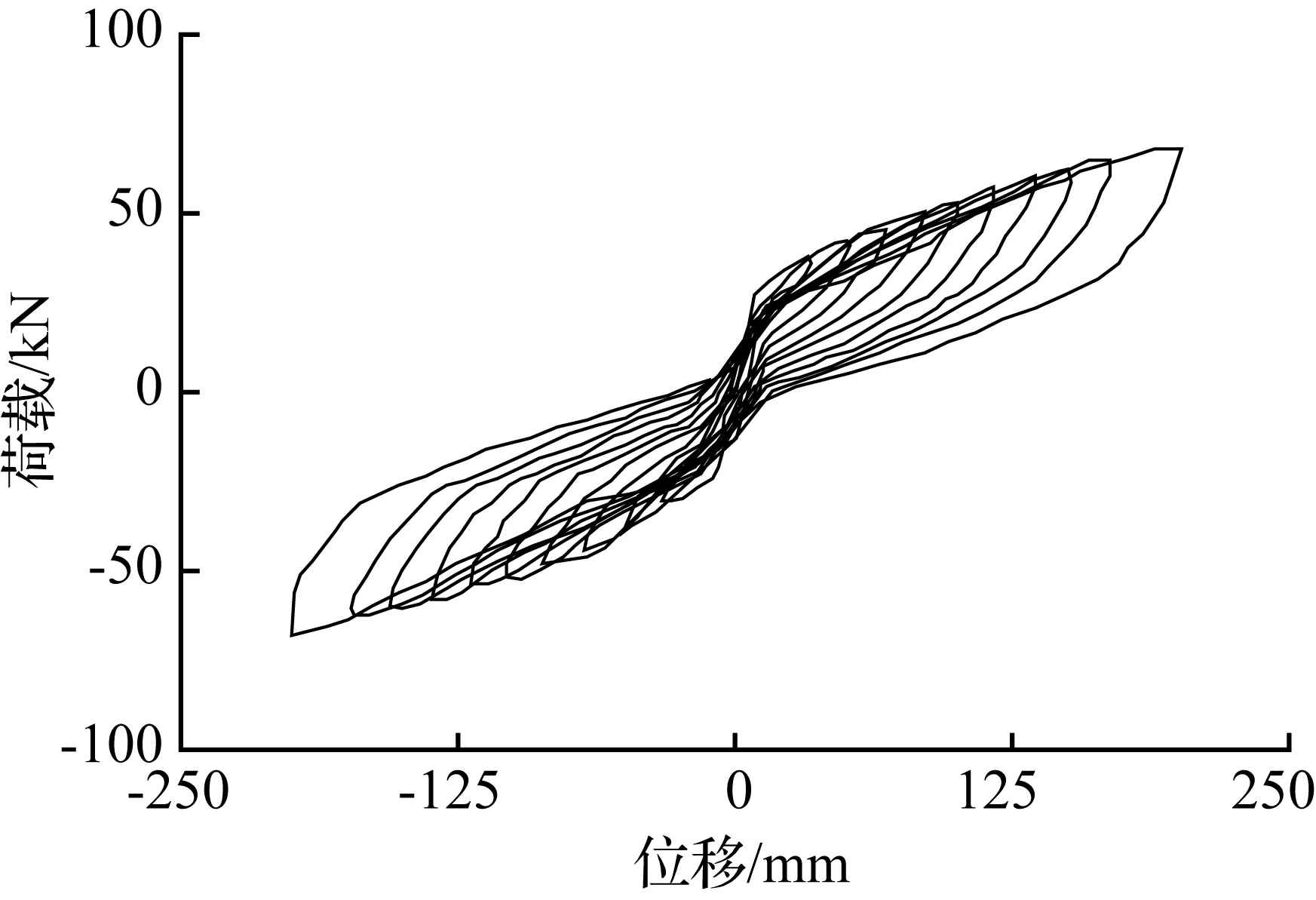
(a) 试验结果

(b) 模拟结果

图2 自复位节点验证对比
Fig.2 Hysteresis curve of self-centering connection

2 高厚比对结构滞回性能的影响

2.1 滞回性能

图3 蝴蝶形钢板剪力墙自复位结构平面布置图Fig.3 Floor plan of self-centering steel frame with infilled butterfly-shaped walls

本研究对一个位于高烈度区六层三跨的钢框架结构进行改造，在四周中间跨布置蝴蝶形钢板剪力墙自复位结构，其平面结构图如图3所示，形成钢框架钢板剪力墙结构，接着选取平面右侧第四层带半层柱的一般层蝴蝶形钢板剪力墙自复位结构进行抗震性能分析。结构的几何参数如图4所示，层高3 600 mm，跨度5 100 mm，试件中n=13，m=2，a=50 mm，b=130 mm，短柱高L=780 mm，布置3排6根预应力钢绞线，初始预拉力为200 kN。试件截面尺寸见表1，钢材弹性模量206 GPa，对结构进行低周循环荷载试验，高厚比分别取200、300、400、500和600，考察在水平荷载作用下不同高厚比的内填蝴蝶形板对结构抗震性能的影响。文献[9-10]规定弹塑性位移限值为层高的1/70和1/50，为了便于分析结构的抗震性能，按位移进行加载，加载初始级取层高的0.5%，加载位移极差为层高的0.5%，每级加载1圈，加载极限取层高的4%。

(a) 蝴蝶形钢板剪力墙自复位钢框架结构

(b)蝴蝶形钢板

(c)蝴蝶形短柱

图4 蝴蝶形钢板剪力墙自复位结构示意图
Fig.4 Self-centering steel frame with infilled butterfly-shaped walls

表1 试件截面尺寸
Tab.1 Section size of specimen

构件名称截面尺寸/mm面积/mm2构件名称截面尺寸面积/mm2框架柱H430×400×20×3635960加劲管2匚102548框架梁H700×300×14×2423528蝴蝶板-2900×2100×1029000

注：表中蝴蝶板为Q235B钢，其余为Q345B钢。

由图5可知，滞回曲线在正、负方向基本对称，当荷载较小时，荷载—位移曲线呈现直线，结构处于弹性状态，刚度值基本不变。随着荷载不断增大，结构将进入弹塑性阶段，滞回环面积不断变大，刚度值变小。荷载达到相应位移级后卸载，最终结构在预应力钢绞线的作用下发生回复，并发生一定的残余变形。

图6为不同高厚比蝴蝶形钢板在层间侧移角为4%时的滞回曲线。随着蝴蝶形钢板剪力墙高厚比不断变大，即钢板厚度变小，结构的承载能力降低，滞回曲线捏缩效应加剧，残余变形减小。高厚比为λ=200的蝴蝶形钢板剪力墙自复位结构捏缩趋势不够明显，滞回环略饱满。高厚比λ≥300的蝴蝶形钢板剪力墙自复位结构的滞回曲线趋同，滞回性能趋于稳定，但与高厚比λ=200蝴蝶形钢板剪力墙结构的滞回曲线相差较大。高厚比λ=300为该蝴蝶形钢板剪力墙自复位结构滞回性能的临界值。

图5 不同高厚比结构的滞回曲线

Fig.5 Hysteresis curves with different height to thickness ratios

图6 位移荷载为4%的滞回曲线

Fig.6 Hysteresis curves in loading displacement of 4%

图7 能量耗散系数定义Fig.7 Energy dissipation coefficient

2.2 耗能能力

荷载—位移曲线所围成的面积即为耗能，面积越大，表明耗能能力越强。为了便于比较出不同高厚比蝴蝶形钢板对耗能能力的影响，以高厚比λ=300的耗能作为基准，以其他钢板剪力墙在同级荷载作用下的单位体积耗能与高厚比λ=300的单位体积耗能的比值为耗能效率。能量耗散系数定义如图7所示，为荷载—位移曲线所包围的面积与相应顶点对应的三角形面积的比值，如图7中环形面积与阴影部分面积的比值。能量耗散系数越大，表明滞回曲线越饱满，反之越捏拢。其计算公式为：

(1)

由图8(a)可见，随着循环荷载的逐级增加，结构的耗能也逐渐增大。这表明结构从不发生耗能的弹性阶段变化到以发生耗能为主的塑性阶段。高厚比λ=200的蝴蝶形钢板剪力墙自复位结构的耗能近乎是同级荷载作用下其他高厚比的2倍。当高厚比λ≥300时，同级荷载作用下的钢板剪力墙耗能逐渐趋于稳定。耗能效率的计算结果如图8(b)所示。结果表明：在荷载加载初期(约为层高的1%时)，高厚比越小，耗能效率越高；加载中后期与初期不同，高厚比越大，耗能效率越高。综合来看，高厚比λ=300的蝴蝶形钢板在整个加载段耗能效率更优。图8(c)所示为不同高厚比的蝴蝶形钢板剪力墙自复位结构在各级加载下的能量耗散系数，同一高厚比蝴蝶形钢板的耗散系数先增大后减小，约在层间位移角为2%时最为饱满。原因是此时以蝴蝶形短柱弯曲变形耗能为主，而随着荷载继续增大，蝴蝶形短柱耗能能力耗尽，其余板件继续耗能，耗散系数较低。同一加载级中，耗散系数随着高厚比的减小而增大，滞回曲线越来越饱满。高厚比λ>300的蝴蝶形钢板剪力墙的能量耗散系数趋向稳定。

2.3 蝴蝶形板面外位移

不同高厚比在各级荷载作用下的面外最大位移如图9所示。高厚比λ=200和300时，当荷载较小时，结构处于弹性状态，面外位移较小，随着荷载的加级，面外位移增大。但当高厚比λ=400时，随着荷载的增加，面外位移出现波动。这是因为在循坏荷载作用下薄板墙板容易出现大范围的折曲，一个点的面外位移被周边相关区域的面外变形弱化，而板较厚时面外位移一般只会随着荷载的增大而增大。这一点应在蝴蝶形钢板剪力墙自复位结构设计中加以利用。

横向加劲肋把蝴蝶形钢板分成了上下两块，荷载面外滞回曲线的位移测点是下半块板的几何中心点。图10分别为高厚比λ=300和λ=500的蝴蝶形钢板剪力墙在循环荷载作用下的面外滞回曲线。高厚比λ=300的蝴蝶形钢板剪力墙面外位移出现正向和负向，面外位移朝单边方向发展的趋势较为明显，呈现收敛的趋势。这种单向位移趋势虽然大大降低了钢板的抗剪强度，但利于钢板耗能。高厚比λ=500的蝴蝶形钢板剪力墙自复位结构在加载初期和中期的面外位移杂乱无章，呈发散趋势，不利于耗能。

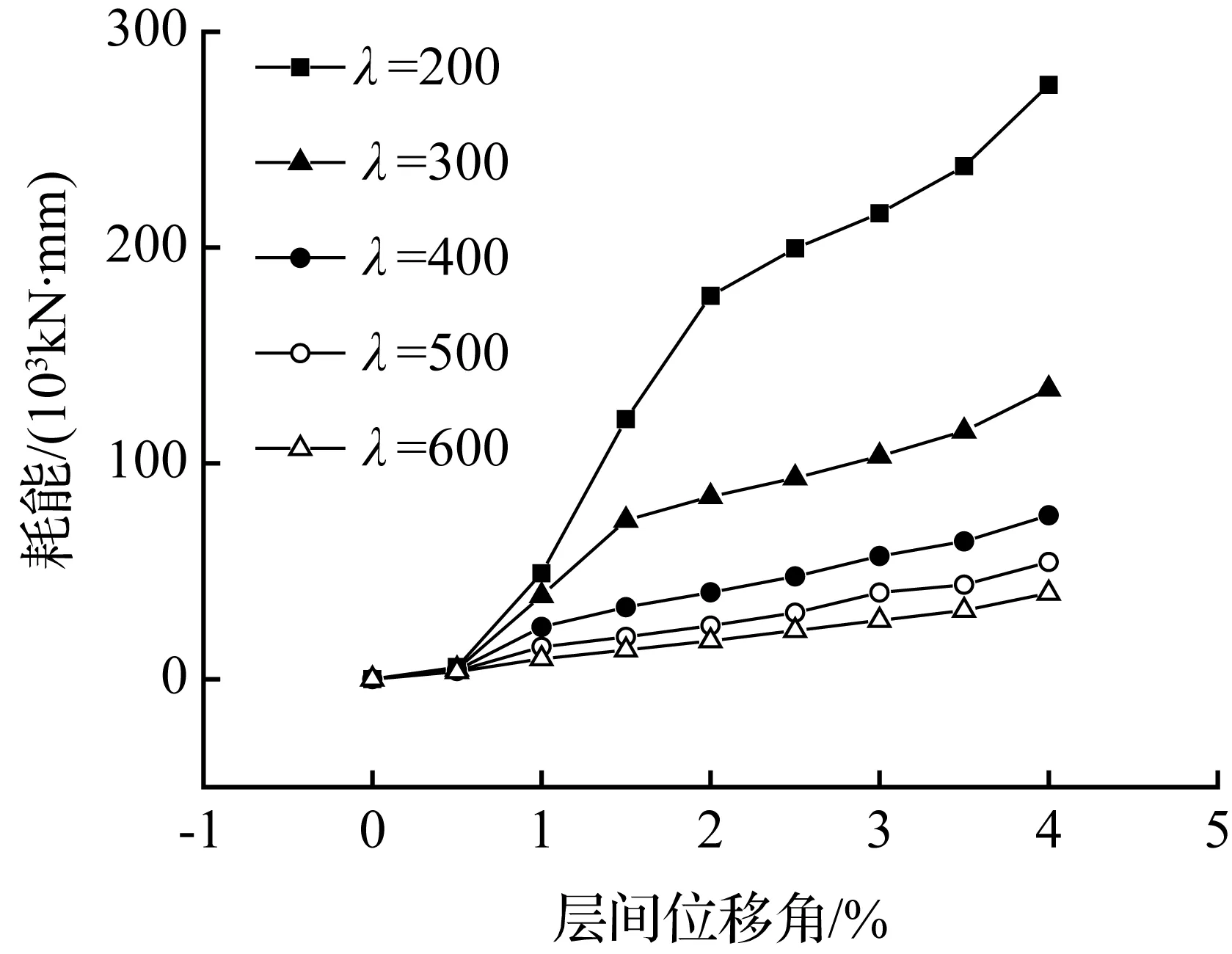
(a) 耗能

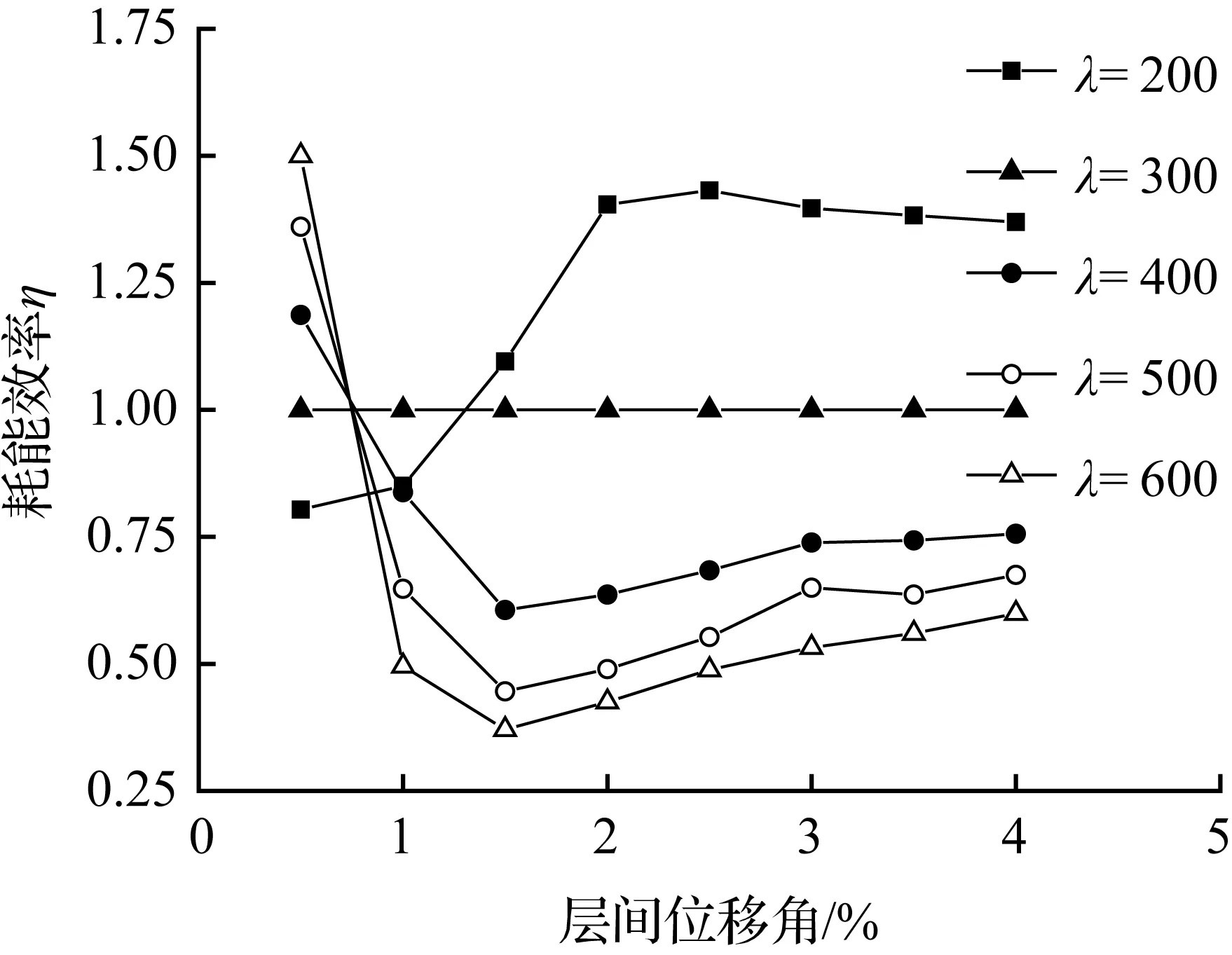
(b) 耗能效率

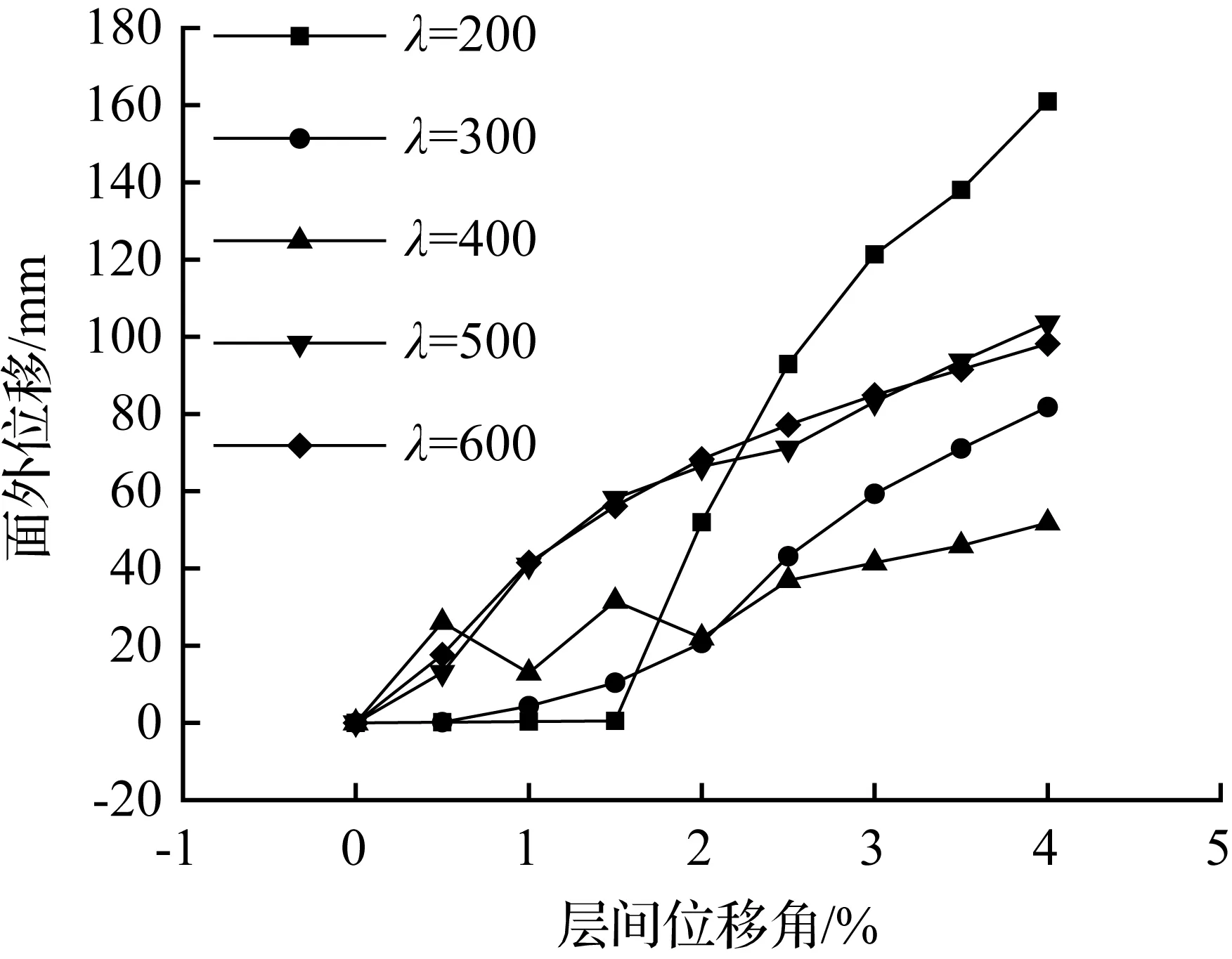
图9 面外最大位移Fig.9 Maximum deformation out of plane

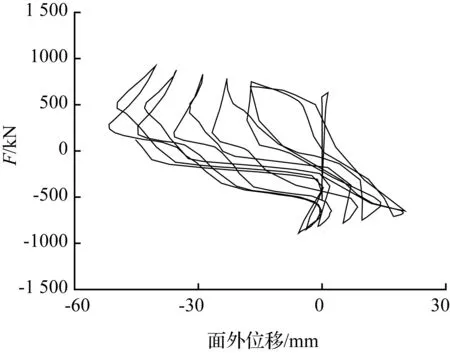
(a)λ=300的面外滞回曲线

(b)λ=500的面外滞回曲线

图10 面外滞回曲线
Fig.10 Relation curves between base shear force and deformation out of plane

3 高厚比对结构刚度和延性的影响

3.1 刚度

定义折算刚度为水平荷载与结构层间水平位移的比值。不同高厚比的蝴蝶形钢板剪力墙的折算刚度如图11所示。结构的刚度随着循环荷载值的不断增加而不断降低。高厚比λ=200的蝴蝶形钢板剪力墙刚度退化速度较快，当高厚比λ≥400时，刚度退化的速度不断接近和趋同。

3.2 延性性能

骨架曲线的绘制方法是将同方向各加载级的顶点值顺次连接。结构的骨架曲线如图12所示。可见，当荷载较小时，结构曲线为直线，随着荷载不断增大，曲线呈现非线性的特点，具有较好的变形能力。随着高厚比的减少，同一位移加载级对应荷载值不断增大。弹性阶段，高厚比λ=200时的刚度值约为高厚比λ=600的1.5倍。由于分析模型中采用了双线性的本构关系，荷载—位移曲线在后期处于缓慢上升的过程，不易找到明显的屈服点，不妨设定层间位移角为4%时对应荷载值为极限荷载Pu，运用通用弯矩法确定Py，这里的Py并不是结构应力第一次出现屈服对应的值，而是结构的关键截面出现屈服对应的荷载值。定义Kyu=(Pu-Py)/(Δu-Δy)，Kyu反映了结构从屈服阶段变化到极限破坏阶段的快慢，Kyu的值越大，说明屈服段长度小，延性差，抗震性能越差。定义延性系数μ=Δu/Δy，延性系数越大，说明结构的延性越好。定义刚度衰减系数β=Ky/K0，Ky为结构屈服时对应的割线刚度，K0为结构的弹性刚度，刚度衰减系数β反映了结构刚度弱化的程度，其值越大越有利。不同高厚比钢板剪力墙的性能参数计算结果见表2。计算表明：高厚比λ≥300的蝴蝶形板各项性能参数趋同，高厚比λ=200和300的蝴蝶形板性能略优于其他高厚比的蝴蝶形板。

图11 刚度退化曲线

Fig.11 Stiffness degradation curse

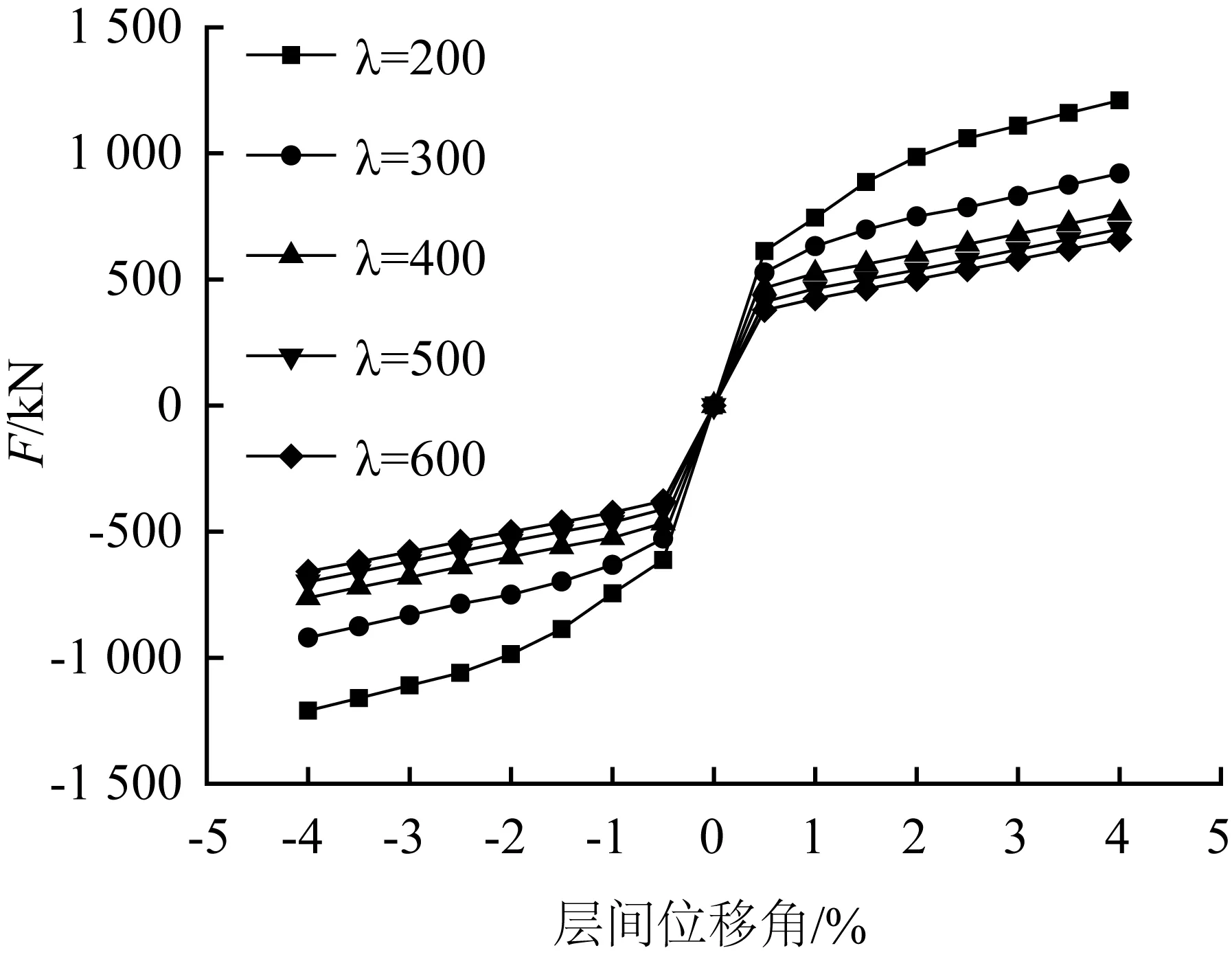
图12 骨架曲线

Fig.12 Skeleton curves

表2 不同高厚比性能参数比较
Tab.2 Comparison of behavior parameters with different height to thickness ratios

λPy/kNΔy/%Pu/kNμKyu/(kN·mm-1)β20072108512124743205730062009392043271039400567097762411780355005080976994117503460045610065840187033

注：Δu为层高的4%，Δy为水平位移与层高的比值。

4 高厚比对结构复位性能的影响

4.1 残余变形

图13 残余变形Fig.13 Residual deformation

在循环荷载作用(荷载先增大再减小，循环往复)下，当荷载回到零时结构对应的残余变形值是衡量复位效果的重要指标。不同高厚比的钢板剪力墙在不同加载级下的残余变形值如图13所示。当荷载较小时，结构处于弹性状态，结构通过自身能完全复位。随着荷载继续增大，结构处于弹塑性状态，结构在预应力钢绞线作用下回复，残余变形增大的趋势得到控制。荷载达到一定值后，薄板率先进入弹塑性，刚度值减小，残余变形比厚板小，高厚比200的残余变形明显大于其他高厚比的残余变形值，当高厚比λ>300时，残余变形趋向于稳定。

4.2 复位性能的理论解释

结构的复位效果主要与结构的刚度和回复刚度有关。结构的刚度是当结构发生弹塑性变形时对应的刚度值，回复刚度与预应力钢绞线的布置和性能参数有关。蝴蝶形钢板剪力墙的刚度计算方法[11-13]是先分别计算上下无孔板带、中间无孔板带和蝴蝶形短柱的刚度，然后再运用串联公式计算。各板带计算公式为：

上下板带：

(2)

中间板带：

(3)

蝴蝶形短柱：

(4)

式中，G为钢板剪切模量；t为钢板墙厚度；W为钢板墙整体宽度；E为钢板弹性模量；Hu为钢板上壁高度；Hm为钢板中间壁高度；Hd为钢板下壁高度；b为蝴蝶形短柱端部宽度；L为蝴蝶形短柱的高度。

假定框架柱轴向刚度无限大，忽略压缩变形，框架梁的抗弯刚度和轴向刚度均为无穷大。设梁柱在水平荷载作用下相对转角为θ，梁柱产生的相对侧移为Δ′，层间侧移为Δ，层高为H，梁高为d，则有如下几何关系：

θ=Δ/H，

(5)

Δ′=θd=Δd/H。

(6)

层间位移角为2%时，框架梁、柱仍处于弹性，该结构能够复位[14]需满足：

(7)

表3 不同高厚比复位性能理论计算
Tab.3 Theoretical calculation of self-centering performance with different height to thickness ratios

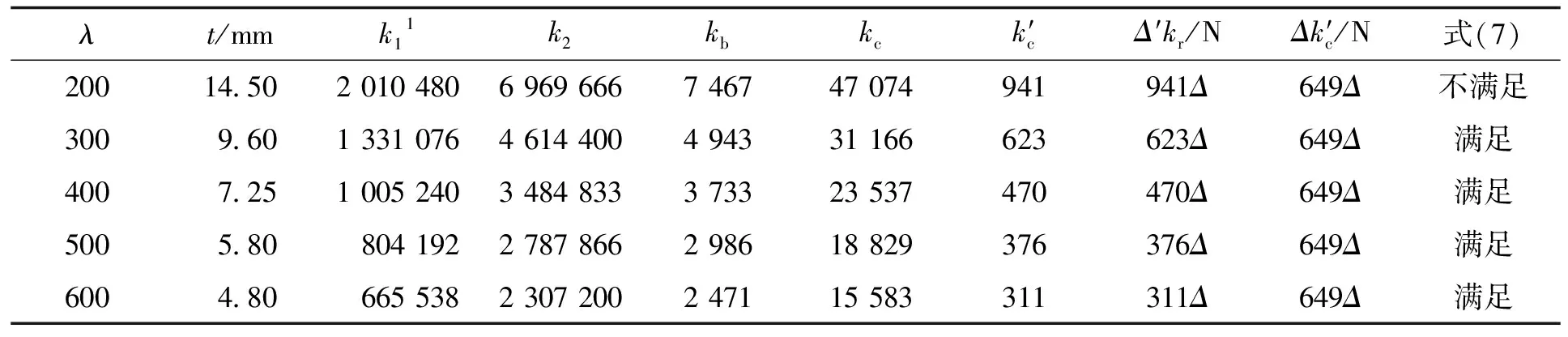
λt/mmk11k2kbkck′cΔ′kr/NΔk′c/N式(7)200145020104806969666746747074941941Δ649Δ不满足30096013310764614400494331166623623Δ649Δ满足40072510052403484833373323537470470Δ649Δ满足5005808041922787866298618829376376Δ649Δ满足6004806655382307200247115583311311Δ649Δ满足

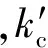
节点的转动刚度：

(8)

回复刚度：

(9)

式中，kpt为预应力钢绞线刚度；kHBE为梁的刚度。由式(5)～(7)可得：

(10)

5 结论

本文利用有限元软件，用壳单元模拟框架梁、框架柱和蝴蝶形钢板剪力墙，杆单元模拟预应力钢绞线，可以得出以下结论：

①结构的耗能随着加载级的增加而增加，随着蝴蝶形钢板剪力墙高厚比的不断减小，同级加载下的结构耗能不断增长；加载初期，厚板的耗能效率较低，之后耗能效率显著提高。高厚比λ=400的面外变形呈现波动的特点。当蝴蝶形钢板剪力墙的高厚比λ>300时，滞回性能趋同。

②结构的刚度随着荷载级的增加而减小，高厚比较小的结构刚度退化速度较快，结构的承载力和刚度值随高厚比的减小而增大，但高厚比λ>300时，刚度和延性性能趋同。

③残余变形是衡量蝴蝶形钢板剪力墙自复位结构的复位性能的重要指标，高厚比λ=200结构的复位性能远差于高厚比λ≥300的复位性能。复位刚度理论可用于计算结构最小高厚比。

综合分析，两端只与梁相连的不同高厚比蝴蝶形钢板剪力墙自复位结构，高厚比λ=300时结构抗震性能更优，建议高厚比控制在300左右。

[1] 陈绍蕃.钢结构设计原理[M]. 北京:科学出版社,2003.

[2] CLAYTON P M, BERMAN J W, LOWES L N.Seismic design and performance of self-centering steel plate shear walls[J]. Journal of Structural Engineering,2011,138(1):22-30.

[3] CLAYTON P M, WINKLEY T B.Experimental investigation of self-centering steel plate shear walls[J]. Journal of Structural Engineering, 2011, 138(7):952-960.

[4] DOWDEN D M, PURBA R, BRUNEAU M.Behavior of self-centering steel plate shear walls and design considerations[J]. Journal of Structural Engineering,2012,138(1):11-21.

[5] 马磊,李启才.蝴蝶形钢板墙的抗侧刚度和承载力研究[J]. 苏州科技大学学报(工程技术版),2015,28(1):30-36.

[6] 朱昱,李启才.利用钢板剪力墙耗能的自复位结构抗震性能研究[J]. 建筑钢结构进展,2015,17(4):19-26.

[7] 李峰,李慎.钢板剪力墙抗震性能的试验研究[J]. 西安建筑科技大学学报(自然科学版),2011,43(5):623-630.

[8] 潘振华,潘鹏,邱法维,等.具有自复位能力的钢结构体系研究[J]. 土木工程学报, 2010, 43(S1): 403-410.

[9] 中国建筑科学研究院.中华人民共和国国家标准建筑抗震设计规范(GB50011-2010)[S]. 北京:中国建筑工业出版社, 2010.

[10]中国建筑技术研究院.中华人民共和国行业标准高层民用钢结构技术规程(JGJ99-1998)[S]. 北京:中国建筑工业出版社,1998.

[11]陈以一,蒋路.帯缝钢板剪力墙的承载力和开缝参数研究[J]. 建筑科学与工程学报, 2010,27(3):109-114.

[12]RICLES J M, SAUES R, GARLOCK M M, et al.Posttensioned seismic-resistant connections for steel Frames[J]. Journal of Structure,2001,127(2):113-121.

[13]李双蓓,刘立国,倪晓慧.结构稳定性研究的现状和新方法的探索[J]. 广西大学学报(自然科学版),2004,29(2):107-111.

[14]CLAYTON P M.Self-centering steel plate shear walls[D]. Washington:University of Washington,2010.

[15]王恒.带缝钢板剪力墙性能研究[D]. 西安:西安建筑科技大学,2006.

(责任编辑唐汉民裴润梅)

Finite element analysis of seismic performance of self-centering steel frame with infilled butterfly-shaped steel plate walls

WANG Yang，LI Qi-cai，WANG Qi，JI Rui

(Structure Engineering Key Laboratory of Jiangsu Province, Suzhou University of Science and Technology, Suzhou 215011，China)

butterfly-shaped steel walls; self-centering structure; height to thickness ratio; hysteretic energy; residual drift

2016-07-15；

2016-08-14

国家自然科学基金资助项目(51378326)；江苏省结构工程重点实验室基金项目(ZD1204)；江苏省2014年度普通高校研究生实践创新计划项目(SJLX_0577 ，SKCX14_039)

李启才(1969—)，男，河南灵宝人，苏州科技大学副教授，工学博士；E-mail：ustsgig@163.com。