基于动态转矩的无刷直流电机机械特性和等效电压系数研究
2017-01-03侯红胜刘卫国马瑞卿
侯红胜, 刘卫国, 马瑞卿
(西北工业大学 自动化学院, 陕西 西安 710072)
基于动态转矩的无刷直流电机机械特性和等效电压系数研究
侯红胜, 刘卫国, 马瑞卿
(西北工业大学 自动化学院, 陕西 西安 710072)
由于无刷直流电机换相过程会造成电枢电流和电磁转矩发生周期变化。在两相导通驱动方式下对电机动态转矩进行分析,并计算平均转矩得到转速——转矩机械特性为非线性,其输出转速小于理想值,从而使等效电压系数小于1。在换相过程中采用关断延迟重叠换相法能够提高电机输出转速,在理论上能够实现电机输出转速等于理想值,等效电压系数等于1。采用两相与三相交替导通的复合驱动方法能够实现输出转速大于理想值,等效电压系数大于1。仿真结果表明复合驱动能在不增加硬件的基础上,扩大了无刷直流电机的输出功率和调速范围。
无刷直流电机;动态转矩;机械特性;等效电压系数;重叠换相;复合驱动
无刷直流电机具有结构简单、出力大、效率高、控制灵活等特点,在航空航天、机器人、汽车电子、精密机床和办公自动化等领域得到了广泛应用[1]。主要缘于其采用电子换相代替了机械换相,避免了换相火花等。理想的无刷直流电机具有平顶宽度大于120°的梯形波反电势,在方波电流的驱动下电磁转矩保持平滑稳定,具有与刷直流电机相同的线性转速-转矩机械特性[2]。但由于电枢绕组电感的存在和每60°电角度进行一次换相,无刷直流电机在换相时刻会使得开通相电流不能立即达到稳态值,而关断相电流不能立即降为零,使换相过程变得复杂。在不同的调制方式和换相控制方式下,会出现电磁转矩不恒定,并影响到传导过程,出现转矩脉动、噪声以及振动等问题。同时,换相会造成无刷直流电机的转速-转矩机械特性为非线性曲线[3]。文献[4-7]分析了不同反电势波形情况换相转矩脉动的消除策略,通过抑制转矩脉动实现了电磁转矩的平滑,只考虑采用电磁转矩与反电势和电枢电流的关系,但均未给出电磁转矩的动态和平均值表达式。文献[8-9]采用动态转矩分析了交流电机的转矩,并通过磁链和电流的控制,形成了转矩的计算公式。文献[10]仅通过反电势系数的估计来计算无刷直流电机的瞬时转矩。文献[11]分析了稳态下电机的等效电压,依然忽略了电机的换相过程对于等效电压的影响。
无刷直流电机在稳速运行时,其转速由于机械惯性保持恒定,但是绕组电流和电磁转矩随着换相过程始终处于周期变化状态,应采用动态转矩分析方法对其瞬时值进行计算。通过求其一个换相周期内平均值来获得转速——转矩机械特性。等效电压是基于PWM调制模式下分析电机的一种方法,从等效电压能够直观看出电机的驱动效果和驱动能力。通过等效电压系数的研究能够得到无刷直流电机的运行状态等。为无刷直流电机的设计、输出驱动能力和利用率提供参考。
1 基于换相的动态过程分析
无刷直流电机及驱动电路等效图如图1所示,电机绕组通常采用三相星形连接方式。图中Ra,Rb,Rc;La,Lb,Lc分别为定子各相绕组电阻和电感,Vdc为直流母线电压,va,vb,vc。为三相绕组端电压,ea,eb,ec和ia,ib,ic分别对应三相绕组反电势和相电流,VN为中性点电压。假设三相电路对称,则Ra=Rb=Rc=R,La=Lb=Lc=L。
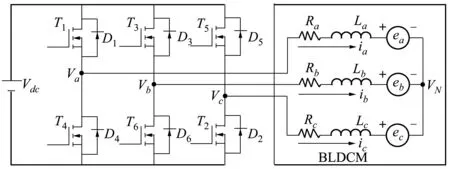
图1 无刷直流电机及驱动电路原理图
两相导通驱动方式理想梯形波反电势与功率器件导通顺序关系如图2所示:
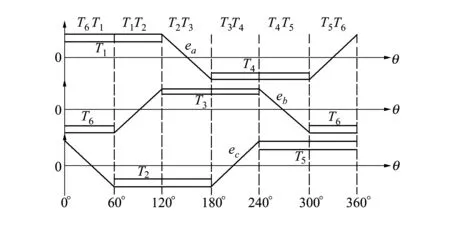
图2 两相导通驱动理想反电势与功率器件导通顺序
在任何时刻只有两相绕组同时导通。每个功率器件导通角度为120°电角度。则电机端电压为
(1)
星形连接方式时,三相绕组电流满足
ia+ib+ic=0
(2)
电机的电磁转矩公式为:
(3)
式中,Te,ωm分为电机的电磁转矩和角速度。
1.1 换相过程分析
无刷直流电机在工作过程中分为换相和传导2个阶段。在常用的两相导通三相六状态驱动方式下,假定施加全电压。在导通阶段,导通的两相绕组通入电流以驱动电机。在换相阶段,由于电感的作用关断相电流不能立即降为零,此时三相绕组均有电流。
以A相为非换相相,B相关断,C相开通下管换相为例,|ib|>0为换相阶段,当ib=0后,进入导通阶段。通常,换相阶段持续时间非常短暂,在气隙磁场为理想梯形波情况下,电机由于机械惯性转速保持恒定,换相期间相绕组反电势保持恒定,等于E或者-E。则绕组端电压方程为
(4)
通常,无刷直流电机电枢绕组电阻值非常小,其压降与电源电压和反电势相比可以忽略不计。假设换相开始时刻有ia=-ib=I0,ic=0,换相期间各相绕组电流为
(5)
当ib=0时,得到B相电流下降时间,即换相时间tf为
(6)
此时C相电流为
(7)
换相结束后,B相电流相为零,C相电流没有达到换相开始时刻的B相电流值,从而造成电磁转矩下降和换相转矩脉动。
1.2 传导过程分析
在传导期间,A、C相电流满足
ia=-ic=i
(8)
电压方程为
(9)
传导期间的初始电流等于上一阶段换相结束时刻电流,由(7)~(9)式可知,传导期间电流为
(10)
(10)式说明,传导期间相电流为单调递增。假设τ为一个换相周期,式中时间参数满足条件0≤t≤(τ-tf)。换相周期τ与电机转速的关系为
(11)
式中,p为电机极对数。
传导期间结束后,进入下一次换相开始时刻,C相电流达到最大值,即换相开始初值I0。将t=(τ-tf)代入(10)式,并令2E=ken,ke为反电势系数,则I0与转速n的关系为
(12)
从(12)式知,无刷直流电机运行过程中最大电流出现在换相开始时刻,其值由电机转速决定。
1.3 基于动态转矩平均值的机械特性
无刷直流电机由于其固有的周期换相,使得相电流在换相和传导期间始终在变化,导致电磁转矩一直处于动态变化。在换相期间,电磁转矩与非换相相电流绝对值成正比。在传导期间,电磁转矩与导通相电流绝对值成正比。在分析电机转速-转矩机械特性时,一般采用平均电磁转矩来求解。结合(5)式和(10)式,一个换相周期内无刷直流电机的平均电磁转矩为
(13)
式中,kT为转矩系数。
2 等效电压系数
由前文分析可知,由于换相过程造成了转矩脉动,从而影响了电机的机械特性。在相同的电磁转矩下,电机输出转速有所下降。原因是由于电机的电阻和电感压降所致。通常,很多文献认为换相时间很短,常给予忽略,只考虑导通期间状态,此时,电压方程为
(14)
式中,D为采用PWM斩波控制时占空比,在全电压状态下D=1。
理想状态下,电机绕组通入方波恒定电流,电压由反电势和电阻压降组成,没有电感压降。此时其工作状态与有刷直流电机一致,电压方程为
DVdc=2E+2RI
(15)
实际上,无刷直流电机由于换相会造成相电流在换相和传导期间电流一直在变化,在电阻和电感中均会产生压降,电压利用率降低。电感上压降为电流变化引起,会随着电流的变化而改变。为了与通常意义上的电压方程表示相同,且与理想电压方程相对应,可引入等效电压系数来分析无刷直流电机电压方程:即
αVdc=2E+2RI
(16)
式中,α为等效电压系数。
与(15)式相比,等效电压系数理想值等于PWM占空比值。在全电压下的固有机械特性中,换相和导通过程中电感始终产生了一部分压降,反电势不能达到理想状态,输出转速小于理想值,使得等效电压系数α<1,相当于电压利用率降低。
3 重叠换相
在换相时刻引入重叠换相,最初是为了消除无刷直流电机换相转矩脉动。同时能够优化电机的机械特性,提高电机的输出转速和功率。但在无刷直流电机的重叠换相过程中,使关断相延时关断,并对其采用PWM调制技术,通过计算合适的占空比,能抑制和消除换相转矩脉动。在A相为非换相相,B相到C相下管换相过程中,当PWM为低时,即关断相关断,此时绕组电压方程同(4)式。当PWM为高时,关断相导通,端电压方程为
(17)
在一个PWM周期内A相绕组电流的平均变化率为
(18)
式中,DO为重叠换相时延迟关断相PWM调制占空比,令其等于零,可得到
(19)
此时,一个PWM周期内B相绕组电流下降速度等于C相绕组电流的上升速度。非换相A相绕组电流保持恒定值,传导期间,导通相电流保持恒定,电磁转矩一直保持恒定。传导期间电压方程表达式与(15)式一致,此时等效电压系数α=1。电机机械特性为
(20)
可见,无刷直流电机转速-转矩机械特性表达式与有刷直流电机相同。相比通用的两两导通换相方式,重叠换相能够保持传导期间的相电流恒定,从而更能够充分利用电压,实现了无刷直流电机机械特性的线性化,而且此方法易于实现。这种线性机械特性使无刷直流电机更加适合高精度控制领域应用。
4 复合驱动
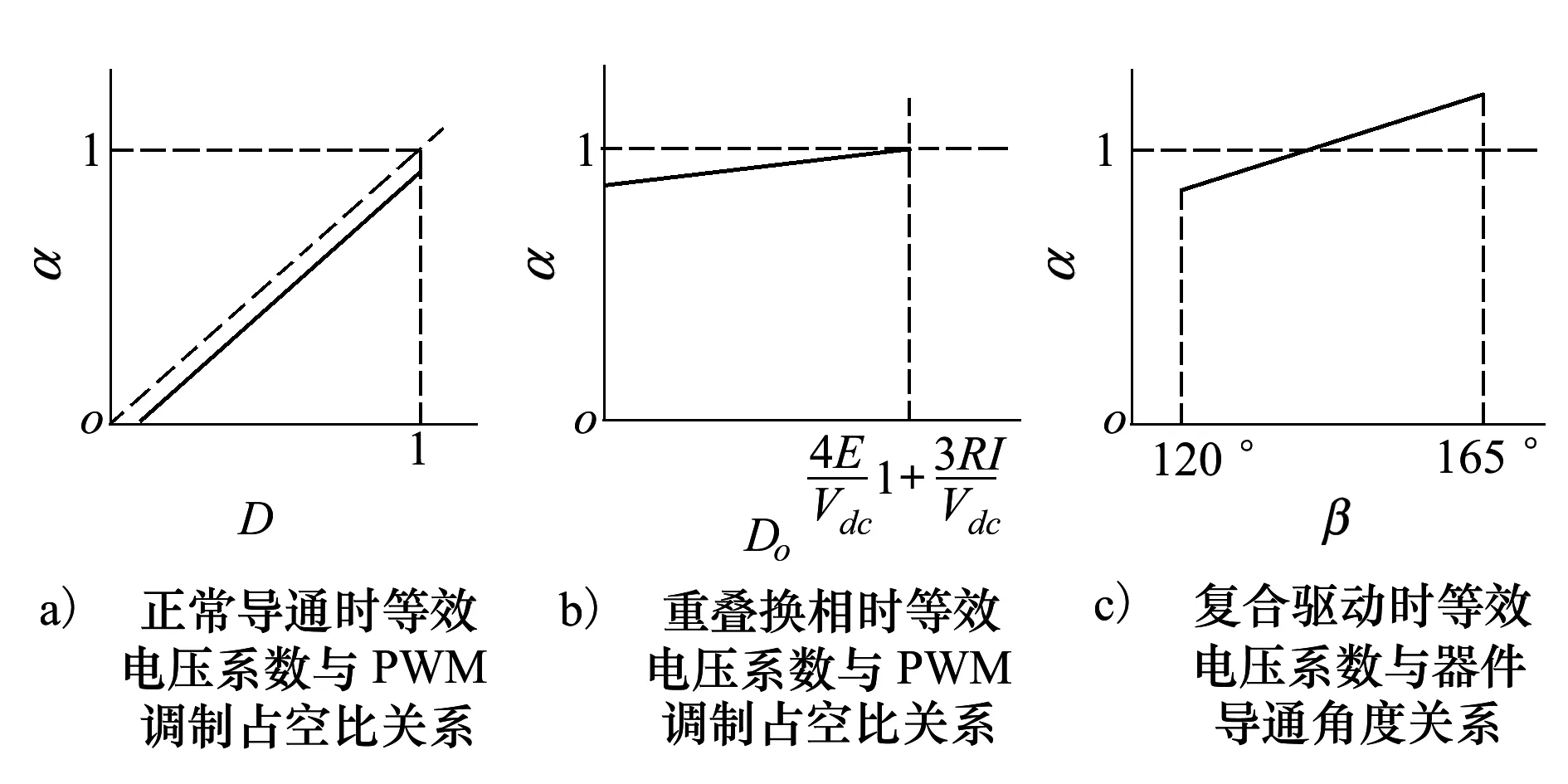
无刷直流电动机两相导通驱动方式中每个功率器件导通角度为120°电角度。其控制简单,易于实现。但是电机的等效电压系数小于1,电压不能充分利用。通过重叠换相,理论上能够使得电机等效电压系数达到1。但在高转速时,采用(19)式的占空比会使得换相失败,所以只能部分提高等效电压系数。在同步电机驱动方式中通常采用三相导通驱动的方式,每个功率器件导通180°电角度,为正弦控制方式,此方法控制复杂,通常需要精度较高的位置传感器。复合驱动采用了两相导通与三相导通交替进行的方式,功率器件导通角度介于120°和180°电角度,且可以通过软件设置。如图3所示。
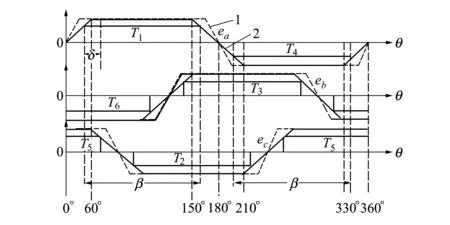
图3 复合驱动反电势与功率器件导通图
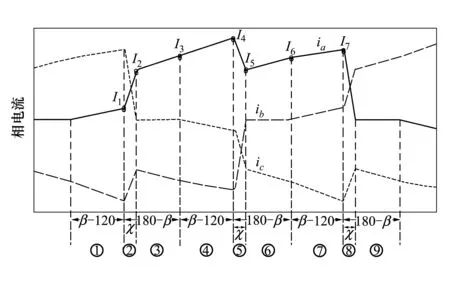
图4 复合驱动A相绕组正半周期电流波形
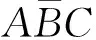
(21)
在过渡阶段,C相关断,由于电感原因,电流不能立即将为零,此时端电压方程为
(22)

根据(21)~(23)式电压方程,忽略电枢绕组电阻压降,电流在不同阶段的变化率有
(24)
由上式可以求得
(25)
并计算换相电角度为
同时可以计算得到各电流值为
在1个周期内,电磁转矩的平均值为
当设置一个导通角度β值,通过取不同的转速,可以求解对应电磁转矩的平均值,得到无刷直流电机在复合驱动下的机械特性。
当β=120°,(28)式与(13)式一致。改变β值能够得到一系列机械特性。当转速不变时,随着β增加,电磁转矩会增加。当电磁转矩保持不变的时候,β增加会引起转速的提高。采用等效电压系数的原则,β增加会使等效电压系数增加,甚至会大于1。同时可以扩大转速的调速范围,不需要弱磁调制也能够实现无刷直流电机在额定转速以上调节。随着功率器件导通角度的增加,导通角度会大于反电势平顶宽度,如图3曲线2所示,导通期间反电势不能保持恒定值,此时,电流的变化会呈现非线性,动态电磁转矩公式会变得非常复杂,但是随着β增加提高电机的输出转速和等效电压系数的规律不变。
5 仿真分析
无刷直流电机的仿真参数设置为:PN=9 kW,Vdc=90 V,IN=115 A,nN=9 180 r/min,R=0.006 Ω,p=2,L=0.032 mH,TN=9.3 N·m。
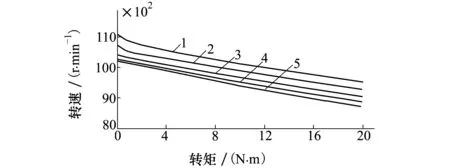
图5是仿真状态下的转速-转矩机械特性曲线图。曲线1、2、3分别为理想状态、重叠换相和基于两相导通换相下的机械特性。在理想机械特性上,等效电压系数α=1,在曲线以下,等效电压系数α<1。
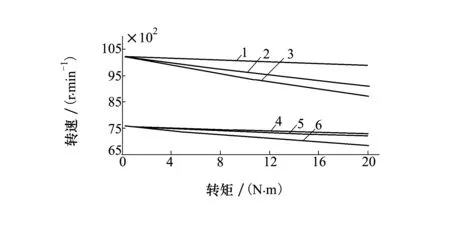
图5 理想特性、固有特性和重叠换相特性
由此可见,固有机械特性的等效电压系数均小于1。在重叠换相过程中,理论曲线与理想机械特性一致,但是当关断相的PWM占空比设置为(19)式的理想值时,会造成换相时间大于换相周期,从而导致换相失败,机械特性为图中曲线2,此时等效电压系数小于1,但是大于固有机械特性时等效电压系数,且转矩脉动有所减小。
曲线4、5、6是采用PWM斩波,且占空比为0.7时的械特性。曲线4与曲线1平行,曲线6为仿真特性,此时等效电压系数α 图6中曲线1~5是功率器件导通角度为160°、150°、140°、130°复合驱动,以及120°正常驱动时转速-转矩特性。此时假设相绕组反电势在对应区域式中保持恒定。当电磁转矩相同时,随着功率器件导通角度的增加,输出转速增加,从而使等效电压系数增加。所有曲线都经过理想空载转速点。 图6 梯形波反电势复合驱动机械特性 实际中,电机反电势由于机械加工,绕组设计和磁钢嵌放等原因,其梯形波恒值区域角度有限,甚至接近正弦波。此时,不同导通角度下机械特性差异变大。图7所示为正弦波反电势时转速-转矩机械特性。曲线1~5与图6中导通角度相同。 图7 正弦波复合驱动机械特性 当电机的反电势为正弦波时,160°导通角度下,额定转矩对应的转速为10 197,比固有机械特性额定转速提高了737 r/min,为7.8%,与固有机械特性的空载转速10 200几乎一致。由此可见,复合驱动不仅能够实现电机转速在固有机械特性向上调节,还能够实现正弦波反电势无刷直流电机在额定负载范围内的理想空载转速稳速运行。 图8是在额定负载时各驱动方式下的等效电压 图8 额定负载时等效电压系数 分析了无刷直流电机在常用两两导通三相六状态驱动方式下换相和传导过程电流和动态电磁转矩,计算平均转矩得到了电机固有机械特性,输出转速低于理想转速,等效电压系数小于1,电压没有充分利用。 采用重叠换相能够在一定范围内改善电机的机械特性,增加等效电压系数。采用复合驱动能够增加电机绕组的利用率,提高等效电压系数,使其等于1甚至大于1, 能够提高输出转速和功率。可以看出,此驱动方式也以适用于供电电压随着能量的消耗而下降的电池供电等应用场合。 [1] 夏长亮, 方洪伟. 永磁无刷直流电机及其控制[J]. 电工技术学报, 2012, 27(3): 25-34 Xia Changliang, Fang Hongwei. Permanent-Magnet Brushless DC Motor and Its Control[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 25-34 (in Chinese) [2] 谭建成. 永磁无刷直流电机技术[M]. 北京:机械工业出版社,2011 Tan Jiancheng. Permanent Magnetic Brushless DC Motor Technology[M]. Beijing, China Machine Press, 2011 (in Chinese) [3] 王晋, 陶桂林, 周理兵, 丁永强. 基于换相过程分析的无刷直流电动机机械特性的研究[J]. 中国电机工程学报, 2005, 25(14): 141-145 Wang Jin, Tao Guilin, Zhou Libing, Ding Yongqiang. Research of the Mechanical Characteristic of Brushless Dc Motor Based on the Analysis of Phase Commutation[J]. Proceedings of the CSEE, 2005, 25(14): 141-145 (in Chinese) [4] Shi Ting, Guo Yuntao, Song Peng, Xia Changliang. A New Approach of Minimizing Commutation Torque Ripple for Brushless DC Motor Based on DC-DC Converter[J]. IEEE Trans on Industrial Electronics, 2010, 57(10): 3483-3490 [5] 石坚, 李铁才. 一种消除无刷直流电动机换相转矩脉动的PWM调制策略[J]. 中国电机工程学报, 2012, 32(24): 110-117 Shi Jian, Li Tiecai. A PWM Strategy to Eliminate Commutation Torque Ripple of Brushless DC Motors[J]. Proceedings of the CSEE, 2012, 32(24): 110-117 (in Chinese) [6] 陈冬, 房建成. 非理想梯形波反电势永磁无刷直流电机换相转矩脉动抑制方法[J]. 中国电机工程学报, 2008, 28(30): 79-83 Chen Dong, Fang Jiancheng. Commutation Torque Ripple Reduction in PM Brushless DC Motor with Nonideal Trapezoidal Back EMF[J]. Proceedings of the CSEE, 2008, 28(30): 79-83 (in Chinese) [7] Xia Changliang, Chen Wei, Shi Tingna. Torque Ripple Reduction in Brushless DC Drives Based on Reference Current Optimization Using Integral Variable Structure Control[J]. IEEE Trans on Industrial Electronics, 2014, 61(2): 738-752 [8] Anshuman Tripathi, Ashwin M. Khambadkone, Sanjib K Panda. Torque Ripple Analysis and Dynamic Performance of a Space Vector Modulation Based Control Method for AC-Drives[J]. IEEE Trans on Power Electronics, 2005, 20(2): 485-492 [9] Auzani Jidin, Nik Rumzi Nik Idris, Abdul Halim Mohamed Yatim, et al. Elbuluk. An Optimized Switching Strategy for Quick Dynamic Torque Control in DTC-Hysteresis-Based Induction Machines[J]. IEEE Trans on Industrial Electronics, 2011, 58(8): 3391-3400 [10] Fang Jiancheng, Zhou Xinxiu, Liu Gang. Instantaneous Torque Control of Small Inductance Brushless DC Motor[J]. IEEE Trans on Power Electronics, 2012, 27(12): 4952-4964 [11] Kamran Tabarraee, Jaishankar Iyer, Hamid Atighechi, Juri Jatskevich. Dynamic Average-Value Modeling of 120°VSI-Commutated Brushless DC Motors with Trapezoidal Back EMF[J]. IEEE Trans on Energy Conversion, 2012, 27(2): 296-307 Mechanical Characteristics and Equivalent Voltage Coefficient Research of BLDC Motor Based on the Analysis of Dynamic Torque Hou Hongsheng, Liu Weiguo, Ma Ruiqing (School of Automation, Northwestern Polytechnical University, Xi′an 710072, China) The phases current and torque will change all the time because of commutation in brushless DC motor. Dynamic torque is analyzed using two devices conducted drive mode. Average torque is calculated to obtain the speed-torque characteristics of BLDCM. It's is a non-linear curve, and the output speed is less than the ideal speed. So the equivalent voltage coefficient is less than one. Using overlapping commutation method can improve the output speed of motor, and it can reach the ideal speed in theory. Then the equivalent voltage coefficient equals one. Compound drive method with two devices and three devices conducted in turns can make the output speed of motor higher than the ideal value, then the equivalent voltage coefficient is larger than one. Simulation results show compound drive method can enlarge the speed change region, and improve the output power. brushless DC motor; dynamic torque; mechanical characteristics; equivalent voltage coefficient; overlapping commutation; compound drive 2016-04-12 陕西省微特电机及驱动技术重点实验室开放课题研究基金(2014SSJ1002)资助 侯红胜(1978—),西北工业大学讲师、博士研究生,主要从事稀土永磁电机及其控制技术研究。 TM351 A 1000-2758(2016)06-1050-07
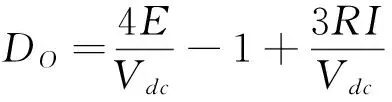
6 结 论
