变体飞行器切换线性变参数鲁棒H∞控制器

何墉, 章卫国, 王敏文, 史静平, 吕永玺

1.西北工业大学 自动化学院, 陕西 西安 710029; 2.洛阳理工学院 电气工程与自动化系, 河南 洛阳 471023 3.飞行器一体化技术重点实验室, 陕西 西安 710072

变体飞行器切换线性变参数鲁棒H∞控制器

何墉1,2, 章卫国1, 王敏文3, 史静平1, 吕永玺1

1.西北工业大学 自动化学院, 陕西 西安 710029; 2.洛阳理工学院 电气工程与自动化系, 河南 洛阳 471023 3.飞行器一体化技术重点实验室, 陕西 西安 710072

针对变体飞行器在不同的机体构型其控制目标不同,提出了一种基于平均驻留时间方法的切换线性变参数(switching linear parameter varying, SLPV)鲁棒H∞控制方法。 该方法根据变体飞行器的任务模式及性能指标要求把后掠角变化范围分成不同的区域, 在不同的区域根据相应的控制目标给出系统满足鲁棒H∞控制性能指标可解的条件及相应的LPV(LPV modeling of morphing aircraft)控制器, 并用平均驻留时间方法保证变体过程的稳定性。仿真结果表明飞行器在变体过程中具有良好的鲁棒性和操纵性能。

变体飞行器;多目标控制;鲁棒H∞控制;LPV控制器;平均驻留时间

变体飞行器是一类能够根据飞行条件和飞行任务而改变其气动外形,始终以最优的飞行状态在大范围变化的飞行环境中完成多种飞行任务[1]。变体飞行器的变体过程主要通过改变机翼的气动外形来实现,机翼形状的改变使得飞行器本体参数如翼面面积、重心位置都随着翼型的改变而改变,由此产生的气动力和动量矩(积)随之发生变化[2],这为变体飞行器的控制带来新的挑战。因此,为了满足飞行品质的要求,所设计的飞行控制系统必须确保变体过程中的飞行稳定性[3]。

线性变参数(linear parameter varying, LPV)控制通过实时可测或可估计的系统参数的变化体现系统的时变特性,可在整个参数轨迹上实现鲁棒稳定性和系统的鲁棒性,在进行系统分析与综合时,其最大的优势在于可用线性系统的处理方法解决非线性问题,因此被广泛地应用于航空、航天系统的控制器设计与研究中[4-5]。系统的性能如稳定性、H∞性能在很大程度上由系统参数集的大小决定,但当参数大范围变换时,单一的LPV控制器将使系统性能变得很差,甚至无法求解。Lu等将LPV控制方法和切换控制理论相结合,提出了一种参变Lyapunov函数的切换线性变参控制(switching linear parameter varying, SLPV)方法[6-7],文献[8]根据变体飞行器的特点及任务模式把后掠角的变化范围分成不同的区域,在各自的区域分别设计控制器,变体时通过激活相应区域的控制器以实现变体过程中的稳定性,但该方法在设计控制器时没有考虑变体飞行器在不同机体构型的控制目标。

变体飞行器相异于常规飞行器的最大优点在于能根据飞行任务的变化而改变机体构型,从而在不同的飞行环境和飞行任务中始终具有良好的飞行性能。由于不同的任务需求及飞行性能要求对应不同的控制目标,因此不同的机体构型其性能指标也不同。文献[6,9]用不同的权值函数来表示F-16战斗机在不同迎角区域的期望性能指标,用参数依赖多Lyapunov函数方法解决迎角大范围变化时的飞行器控制问题。文献[10-11]用迟滞切换和公共Lyapunov函数方法解决变体飞行器变体的快速性问题及变体过程中的多目标控制问题,但采用公共Lyapunov函数方法过于保守;而采用迟滞切换策略时,切换面却因切换序列的不同而不同,这给设计过程带来额外负担,而平均驻留时间方法可弥补上述两种切换策略的不足,解决变体飞行器变体过程中的多目标控制问题。

1 变体飞行器LPV建模

基于如图1所示的某型变后掠翼无人机进行研究, 机翼后掠角χ的变化范围为15°～60°, 这里给出该变体飞行器的纵向短周期非线性动力学模型[10-11]:

图1 变后掠翼飞行器

(1)

对其用Jacobian线性化方法可以得到变体飞行器纵向短周期在平衡点处的线性小扰动方程为

(2)

式中,Δα、Δq和Δδe分别为状态向量和控制向量相对于平衡点处的偏差量。为描述变体动作对飞行器的影响, 在后掠角变化范围内每隔5°作为一个考察基准, 运用CFD软件计算每种构型下的气动参数。为便于分析气动参数和χ的关系, 把变体过程中重心位置的变化对飞机的影响换算为相应构型气动参数的变化。因此, 以后掠角作为调度参数, 定义ρ=χ, 可得到变体飞行器的LPV模型

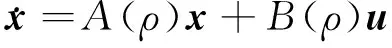
(3)

2 基于参数依赖Lyapunov函数方法的切换LPV控制器设计

2.1 问题描述

考虑如下形式的切换LPV系统模型

∀ρ∈pi

(4)

(5)

式中，xk∈Rnk为控制器的状态。当参数变化到某个区间,激活相应的控制器。因此,在每个参数子区域pi内闭环系统描述为

(6)

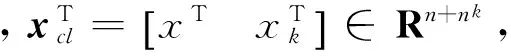
2.2 基于平均驻留时间方法的控制器设计

定理1 给定标量λ0>0,μ>1,考虑开环线性变参数系统(4)和变参数区域P及子区域{pi}i∈ZN,令

若对于任意ρ∈pi都存在一组正定对称矩阵Ri(ρ)和Si(ρ),(i∈ZN)满足如下条件

(10)

(11)

则存在变参数控制器使系统(4)切换信号满足条件

(12)

时在参数区域P内是指数稳定,且对于λ<λ0时系统满足加权H∞性能指标γ

证明对任意参数子区域pi(i∈ZN)内,假设存在一组参数相关正定对称矩阵函数Xi(ρ)在其所属子区域光滑连续,则闭环系统(6)对应于该子区域的Lyapunov函数可定义为

(13)

线性矩阵不等式(7)～(9)等价于

(14)

并且参数相关Lyapunov函数具有如下形式

式中

对上式作等价变化可得

(15)

由不等(14)式易知

(16)

假设在时间间隔[0,T]内的切换时间序列为0,t1,…,tNσ(0,T),t0=0为初始时刻,则

由(12)式易得闭环系统(6)指数稳定。

3 仿真验证

本节基于前文的变体飞行器切换LPV模型进行仿真研究。根据变体飞行器的特点及任务模式将后掠角变化范围分为3个区域, 区域划分为P1:15°≤χ≤30°;P2:30°≤χ≤45°;P3:45°≤χ≤60°,分别对应巡航模态、中间过渡模态和冲击飞行模态。为体现变体飞行器变体过程中在不同的后掠角区域有不同的控制目标,分别选择3个权值函数

相应区域的LPV控制器分别用K1(ρ)、K2(ρ)和K3(ρ)表示。当后掠角变化到相应区域时,相应的控制器被激活, 并通过相应的权值函数实现对变体飞行器的多目标控制。

变体飞行器切换LPV系统的控制结构图如图2所示。

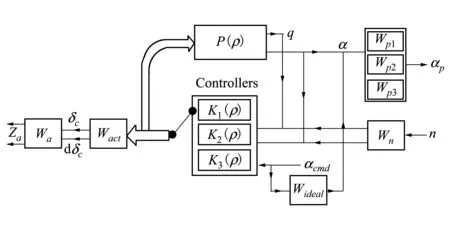
图2 变体飞行器切换LPV系统的结构图

其中P(ρ)是变体飞行器纵向短周期的切换LPV模型, 把系统的2个状态α和q作为输出, 跟踪的理想模型：

其输出αideal和实际迎角输出α的差α-αideal作为跟踪误差,通过权值函数惩罚跟踪误差。外部输入包括二维传感器噪声n和迎角指令信号acmd。被控输出包括开环加权误差信号αp和za,这样就可将跟踪问题转化为外部输入和被控输出之间的H∞控制问题。图2中作动器动态模型Wact取为

控制输入的惩罚函数Wa为

Wa=diag(0.1,0.2)

设各子区域pi(i为所在区域编号)所对应的参数依赖Lypunov函数矩阵Xi(ρ)为

Ri(ρ)=Ri0+ρRi1Si(ρ)=Si0+ρSi1

式中,ρ=χ为变体飞行器的后掠角,矩阵Rij和Sij,(j=0,1)是待优化求解的矩阵。图3给出了变体飞行器用本文所用方法在变体过程中对给定指令信号的响应曲线。

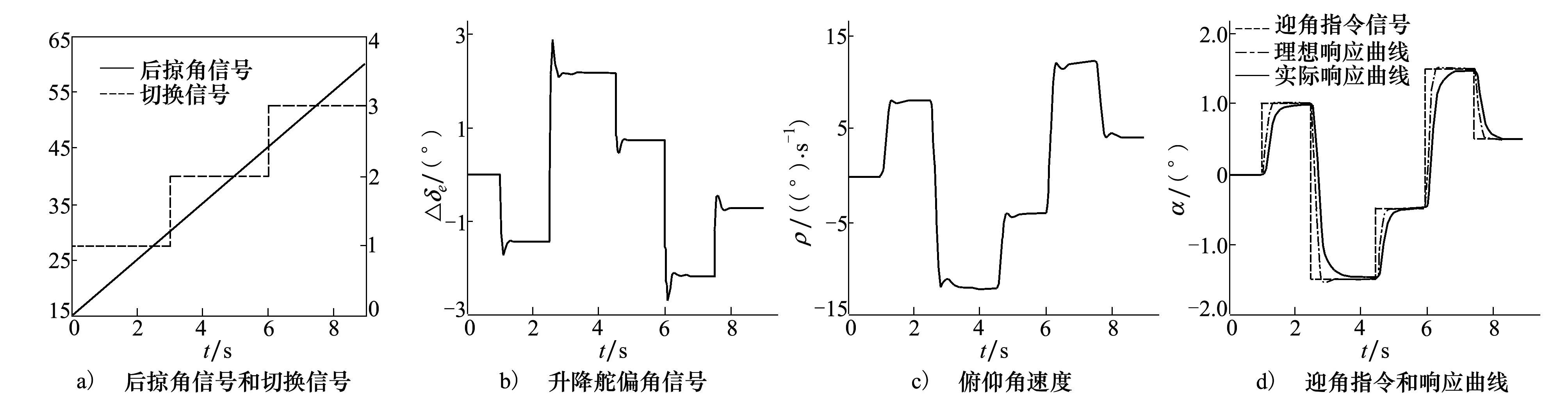
图3 响应曲线

4 结 论

本文基于平均驻留时间的方法设计了变体飞行器切换线性变参数系统的鲁棒H∞控制器,考虑到变体飞行器在不同的后掠角区域其控制目标不同,在设计过程中根据不同的控制目标分别设计相应区域的鲁棒控制器,并用平均驻留时间方法保证变体过程中的稳定性。仿真结果表明用本文所用方法不但能有效降低系统的保守性,同时可使系统的H∞性能明显改善,也可实现对指令信号的良好跟踪。

[1] 陆宇平,何真. 变体飞行器控制系统综述[J]. 航空学报, 2009, 30(10): 1906-1911 Lu Yuping, He Zhen. A Survey of Morphing Aircraft Control Systems[J]. 2009, 30(10): 1906-1911 (in Chinese)

[2] 乐挺,王立新,艾俊强. Z型翼变体飞机的纵向多体动力学特性[J]. 航空学报, 2010, 31(4): 679-686 Yue Ting, Wang Lixin, Ai Junqiang. Longitudinal Multibody Dynamic Characteritics of Z-Wing Morphing Aircraft[J]. Acta Aeronatuca et Astronautica Sinica, 2010, 31(4): 679-686 (in Chinese)

[3] Seigler T M, Neal D A. Analysis of Transition Stability for Morphing Aircraft[J]. Journal of Guidance, Control and Dynamics, 2009, 32(6): 1947-1954

[4] Lee C H, Shin M H, Chung M J. A Design of Gain-Scheduled Control for a Linear Parameter Varying System: an Application to Flight Control[J]. Control Engineering Practice, 2001, 9(1): 11-21

[5] Aplarian P, Gahinet P, Becker G. Self-ScheduledH∞Control of Linear Parameter-Varying System: a Design Example[J]. Automatica, 1995, 31(9): 1251-1261

[6] Lu B, Wu F, Sung Wan K. Switching LPV Control of an F-16 Aircraft Via Controller State Reset[J]. IEEE Trans on Control Systems Technology, 2006, 14(2): 266-277

[7] Lu B, Wu F. Switching LPV Control Designs Using Mutiple Parameter-Dependent Lyapunov Functions[J]. Automatica, 2004, 40(11): 1973-1980

[8] 王青, 杨汇川, 董朝阳. 基于重叠参数区域的变体飞行器切换LPV控制[J]. 沈阳工业大学学报,2013, 35(6): 698-703 Wang Qing, Yang Huichuan, Dong Chaoyang. Switching LPV Control of Morphing Aircraft Based on Overlapped Parameter Area[J]. Journal of Shenyang University of Technology, 2013, 35(6): 698-703 (in Chinese)

[9] 何旭. 切换线性变参数系统的H∞控制及其在飞行器系统中的应用[D]. 沈阳：东北大学,2011 He Xu. Control of Switched Linear Parameter Varying Systems and Its Application to Air Vehicle[D]. Shenyang, Northeastern University, 2011 (in Chinese)

[10] 何墉,章卫国,王敏文,等. 基于多目标控制的变体飞行器切换线性变参数控制器[J]. 控制理论与应用, 2015(11): 1518-1525 He Yong, Zhang Weiguo, Wang Minwen, et al. Switching Linear-Parameter-Varying Control for Morphing Aircraft Based on Multi-Objective[J]. Control Theory & Application, 2015, 32(11): 1518-1525 (in Chinese)

[11] 何墉,章卫国,王敏文,等. 变体飞行器的切换LPV控制[J]. 西北工业大学学报, 2015, 33(5):781-787 He Yong, Zhang Weiguo, Wang Minwen, et al. Switching LPV Control for Morphing Aircraft[J]. Journal of Northwestern Polytechnical University, 2015, 33(3): 781-787 (in Chinese)

Switching LPV RobustH∞Controller for Morphing Aircraft

He Yong1,2, Zhang Weiguo1, Wang Minwen3, Shi Jingping1, Lü Yongxi1

1.School of Automation, Northwestern Polytechnical University, Xi′an 710029, Chinab 2.College of Electrical Engineering and Automation, Luoyang Institute of Science and Technology, Luoyang 471023, Chinac 3.Key Laboratory of Science and Technology on Aircraft Control, Xi′an 710072, China

A morphing aircraft has different control objectives in different configurations. For the multi-objective-control problem of the morphing aircraft, a robust controller of theswitchinglinear parameter varying(SLPV) is proposed based on the average dwell time switching scheme in which the range of the sweep angle is divided into sub-regions according to the flight modes and design objectives, and the solvability condition of the problem with a given robust performance indices is established and a group of the LPV controllers is designed accordingly, meanwhile, the average dwell time scheme of switching is adopted to maintain the stability and the control performance of the aircraft in morphing. At last simulation results are used to showthat the designed controller can guarantee the excellent robustness and control performance.

morphing aircraft; multi-objective-control; robust control; LPV controller; average dwell time

2016-04-19

国家自然科学基金(61374032)与航空科学基金(20140753012)资助

何墉(1980—)，西北工业大学博士研究生，主要从事变体飞行器控制方法研究。

V241.62

A

1000-2758(2016)06-1045-05