水下通信用光缆线包缠绕力学建模及仿真

汤伟江, 刘卫东, 陈刚, 杨贺然, 张建军

1.西北工业大学 航海学院, 陕西 西安 710072; 2.中国船舶重工集团公司第705研究所, 陕西 西安 710077;3.西北工业大学 水下信息与控制重点实验室, 陕西 西安 710072

水下通信用光缆线包缠绕力学建模及仿真

汤伟江1,2, 刘卫东1,3, 陈刚2, 杨贺然2, 张建军1

1.西北工业大学 航海学院, 陕西 西安 710072; 2.中国船舶重工集团公司第705研究所, 陕西 西安 710077;3.西北工业大学 水下信息与控制重点实验室, 陕西 西安 710072

因电磁波无法在水中传播,水下大容量长距离通信仅能依靠光缆等有线通信方式。对于水下航行器等需随航行体运动实时布放光缆以建立动态通信信道的应用场合,光缆线包缠绕工艺及缠绕机构的优化设计,对减小断线概率、提高水下通信的可靠性显得尤为重要。在对光缆缠绕过程及端板力学分析的基础上,提出一种以各层光缆径向变形和轴向变形为增量的逐层分析方法,建立了水下通信用光缆线包缠绕力学模型。该模型揭示了缠绕过程光缆线包内张力分布及端板变形的内在规律,以实际光缆线包结构参数和缠绕工艺参数对光缆线包内部应变、光缆层压强以及端板变形进行仿真分析,仿真结果与光缆线包缠绕过程应变实测数据符合性好。

水下航行器;光缆线包;缠绕力学模型;光缆轴向应变;端板变形

光纤通信是水下系统实现远程大容量通信的优选通信方式。将光纤通信技术应用于水下航行器,有利于实现其与母船的双向大容量信息传输,而水下航行器要求实时布放与之运动相匹配的光缆,以建立动态可靠通信信道。光缆线包是水下航行器光缆布放系统的核心部件,由单根光缆分层紧密缠绕而成,缠绕时需对光缆施加一定的缠绕张力,以使光缆能在一定张紧条件下绕入线包,缠绕张力的存在使光缆线包各层光缆存在内张力,内张力的分布状态影响光缆线包的整体性及在大深度水下的使用性能;内张力的存在使光纤产生应力,决定光缆线包的使用及贮存寿命[1];光缆线包缠绕时,各层光缆因径向受压会产生轴向变形,进而导致缠绕过程两侧端板的变形,在安装壳体并去除芯轴后,端板变形恢复会引起线包内部开裂甚至塌方,大幅降低光缆线包的布放性能。因此,准确分析缠绕过程光缆的内张力以及对端板施加的轴向力分布,可指导光缆线包缠绕工艺及缠绕机构的设计。

国内外学者对纤维增强复合材料、大扬程起重设备的钢丝绳、导弹用制导光缆线包缠绕等缠绕力学特性领域已开展了相关研究工作并取得了一些成果。针对纤维增强复合材料缠绕力学特性的研究主要是利用复合材料的三维本构关系,建立内衬及各层纤维的应力应变模型,分析内衬和各层复合材料应力[2-3]以及内衬厚度[4]、缠绕角度[5]和缠绕张力[6-8]对应力分布的影响并研究缠绕张力的设计方法。胡勇等针对双折线卷筒钢丝绳的排列方式,建立了钢丝绳多层缠绕系数方程,并对多层缠绕系数及内张力分布进行了仿真[9],由于钢丝绳的松散缠绕特性,并未考虑同层钢丝绳匝与匝之间的相互作用。马成举等建立了导弹用制导光缆线包层间压强模型,在模型中以卷盘径向收缩形变系数常量来表示缠绕过程卷盘和光缆层的变形,并对缠绕过程光缆层压强进行仿真分析和实验验证[10]。

钢丝绳缠绕为松散缠绕,复合材料及导弹用制导光缆缠绕架均没有两侧端板,而水下航行器光缆线包为分层双向紧密缠绕,缠绕架由芯轴和两侧端板组成,其缠绕方式、缠绕架结构与上述研究有较大差异,是缠绕力学特性研究的一个新方向。在分析光缆及端板受力的基础上,研究逐层缠绕时光缆径向压缩、轴向延伸与光缆内张力、轴向挤压力的关系,建立了光缆线包缠绕力学模型;根据实际光缆线包结构参数和缠绕工艺参数,对光缆线包内部应变、光缆层压强以及端板变形随缠绕层数的变化规律进行了仿真研究,并利用高精度光纤应变分析仪对光缆线包的应变进行了实验测量,通过仿真与实测数据的对比,验证了模型的准确性。

1 光缆线包受力分析及模型建立

通过专用绕线机将单根光缆逐层紧密缠绕在缠绕架(如图1所示)上,形成光缆线包。在缠绕过程中,当前层光缆绕入时,已绕各层光缆因挤压而产生径向变形,使各层光缆周向变形减小,轴向变形增大,从而使各层光缆的内张力减小、各层光缆施加在端板上的轴向挤压力增大。端板在各层光缆对应位置的变形量与垂直于端板轴向挤压力呈线性关系,且各层光缆的内张力与其径向变形也呈线性关系。因此,以各层光缆径向变形和轴向变形为增量,形成一种逐层增量分析方法,建立光缆线包缠绕力学模型,研究缠绕过程各层光缆内张力以及对端板轴向挤压力的变化规律。

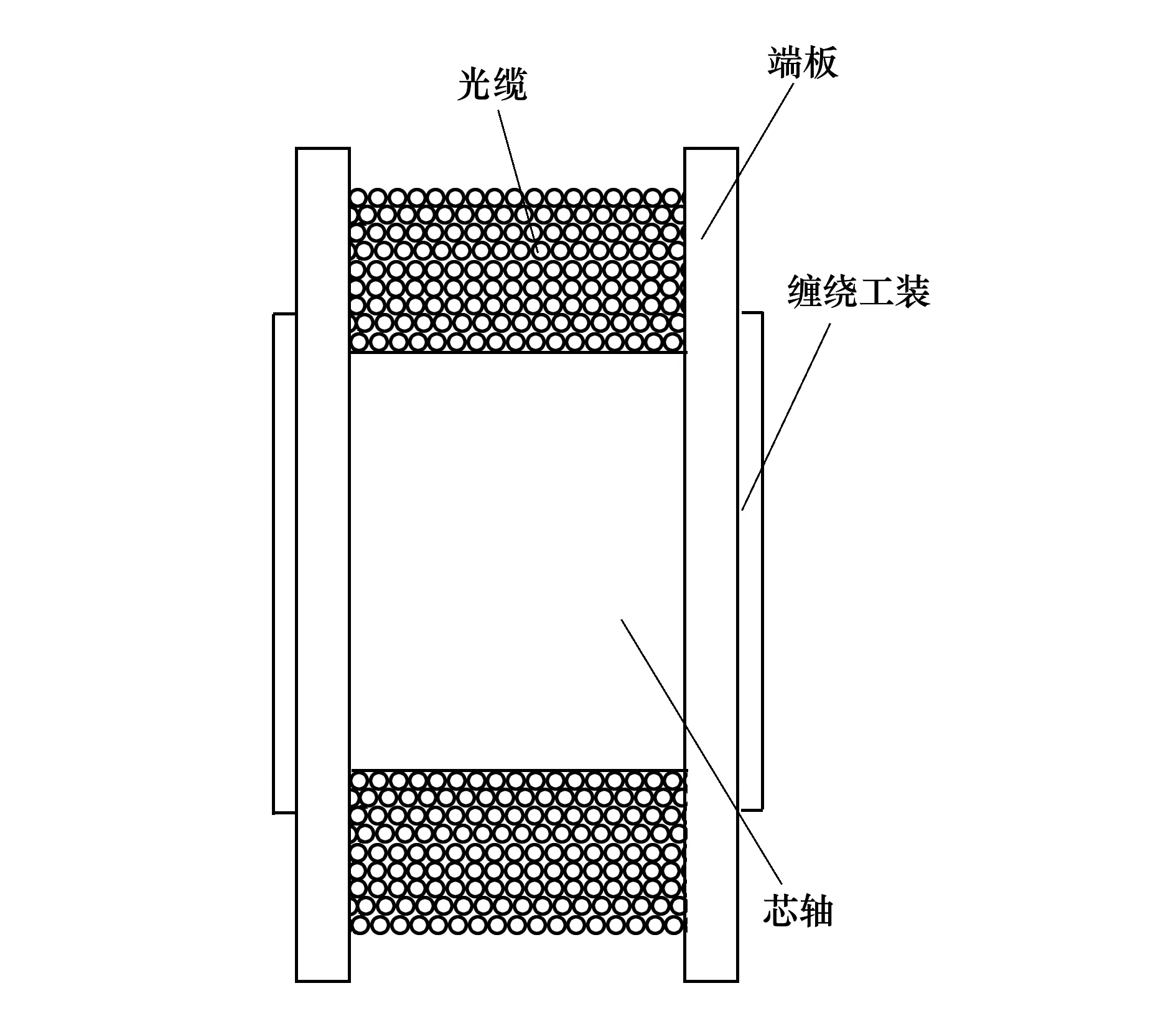
图1 光缆线包及缠绕架结构

1.1 光缆线包受力分析

芯轴与端板之间依靠缠绕工装固连,形成缠绕架后,端板之间位置固定。除第1层外,每层光缆均缠绕在下一层光缆匝与匝之间形成的凹槽内,缠绕当层光缆对两侧端板无轴向力作用。

缠绕第n层光缆时,第i层光缆的径向变形量ΔRi,n与该层光缆的径向压缩量Δri,n、第(i-1)层径向变形量ΔR(i-1),n和第(i-1)层光缆径向压缩量Δr(i-1),n相关,即

(1)

以此类推,第1层光缆仅与该层光缆径向压缩量Δr1,n有关,即

(2)

由此可见,缠绕第n层光缆时,各层光缆的径向变形量与缠绕第n层光缆引起的该层及以下各层光缆的径向压缩量相关,而径向压缩量是由缠绕第n层光缆对内部各层的径向压力增量作用而产生的。

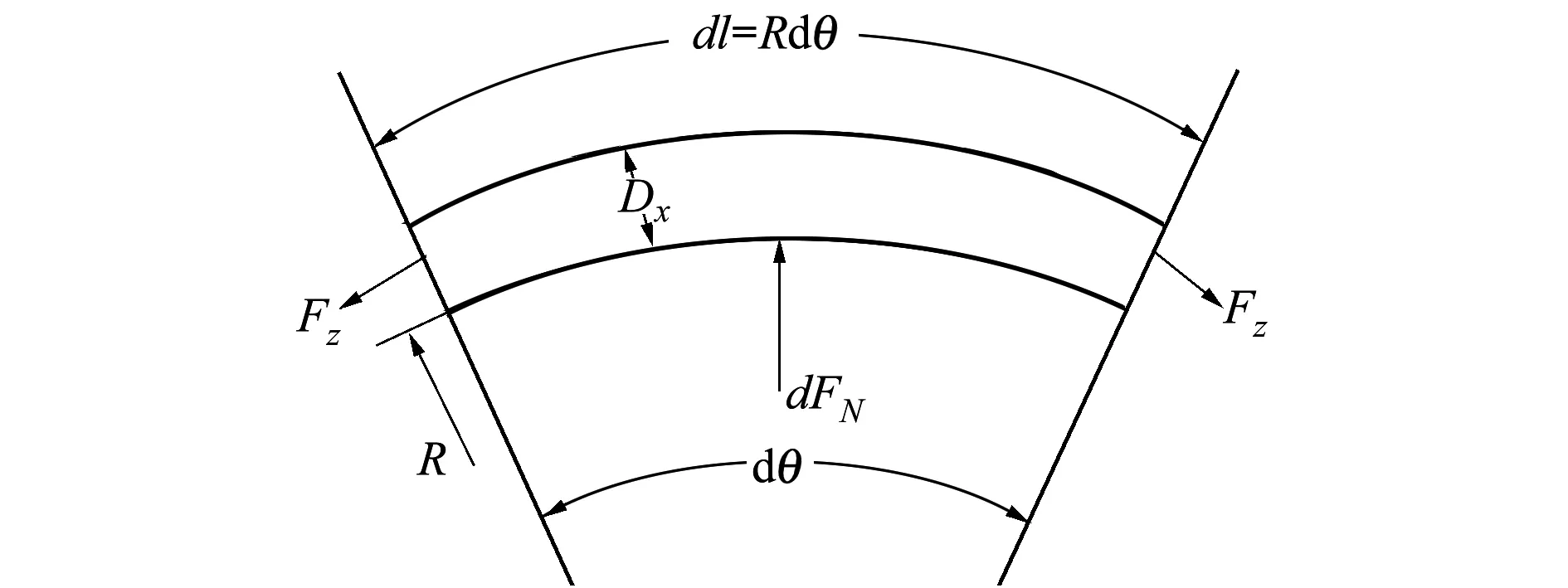
图2 光缆微元受力

取dl长度的已绕光缆微元(如图2所示),缠绕半径为R,dθ为光缆微元对应的张角,Fz为光缆的缠绕张力,dFN为内层光缆施加在该层光缆的支撑力,Dx为光缆直径。

由受力平衡可得

(3)

内层光缆所受压强

(4)

以张角dθ对应的各层光缆微元为研究对象,第(i+1)层、第(i+2)层、…、第n层光缆对第i层光缆均有压力,其大小为各层光缆内张力沿线包径向的合力。当第n层光缆缠绕到线包上时,第(n-1)层光缆所受压力增量为Fzdθ,但是第(n-1)层及以下各层光缆由于第n层光缆的缠绕,内张力分别减小ΔFz(n-1),n、ΔFz(n-2),n、…、ΔFz(i+1),n,相应的各层光缆沿线包径向压力的减小值分别为ΔFz(n-1),ndθ、ΔFz(n-2),ndθ、…、ΔFz(i+1),ndθ,因此由于第n层的缠绕导致第i层光缆在dθ部分所受压力增量dFNi,n为

(5)

由于光缆线包为紧密缠绕,层与层之间变形协调,无相对滑动,层与层光缆之间无摩擦力存在,且同层光缆轴向变形也是协调的,忽略与端板接触的光缆因径向变形而与端板之间产生的摩擦力。

光缆截面受力如图3所示。dFNri,n和dFNxi,n为作用在第i层光缆力的增量,而作用在第i层光缆下侧力的增量应为dFNr(i-1),n和dFNx(i-1),n。这里为简化计算将作用在第i层光缆下侧力的增量近似用dFNri,n和dFNxi,n代替。

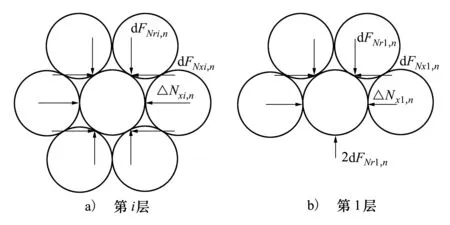
图3 光缆截面受力

(6)

(7)

式中,γ为光缆堆叠角。

光缆径向压缩量为

(8)

式中,Er为光缆径向弹性模量,是单位长度光缆承受的径向压力与光缆径向直径沿压力方向减小量的比值,Wr为光缆径向弹性系数,是与压力垂直方向径向直径的增加量和沿压力方向径向直径的减小量的比值,ΔNxi,n为缠绕第n层时第i层单位长度光缆匝与匝之间的轴向挤压力增量(等于该层光缆对端板的轴向挤压力增量),dli为张角dθ对应的第i层光缆微元的长度,即

(9)

式中,Ri为第i层光缆的半径,Rz为芯轴半径。

同理,可以获得光缆的轴向延伸量为

(10)

1.2 端板受力分析

1) 挤压变形

由于缠绕工装弹性模量远大于端板弹性模量,因此分析时可忽略缠绕工装的变形。Rt为缠绕工装半径,若Rz≤Ri≤Rt(即1≤i≤nt,nt为Rt对应的光缆层数),端板受力如图4所示。

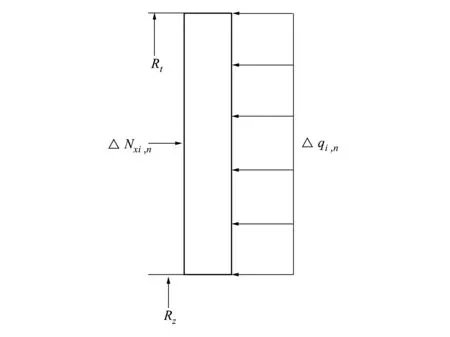
图4 缠绕工装半径范围内端板受力

由受力平衡,可得

(11)

式中,Δqi,n为因缠绕第n层时第i层光缆轴向挤压力增量作用下缠绕工装作用在端板的均布压强增量。

缠绕工装范围内各层光缆对端板施加的力与缠绕工装对端板的作用力相等,即

(12)

则端板挤压变形ΔLbi,n为

(13)

式中,Eb为端板的弹性模量,Lb为端板厚度。

2) 弯曲变形

缠绕工装范围以外各层光缆对端板施加的轴向挤压力将使端板产生弯曲变形。端板满足薄板弯曲理论的基本假设,依据圆形板对称弯曲理论[11],有

(14)

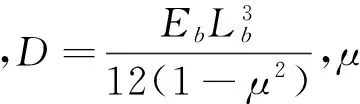
在第i层光缆轴向挤压力作用下,Ri范围内剪力为

(15)

将(15)式代入(14)式,可得

(16)

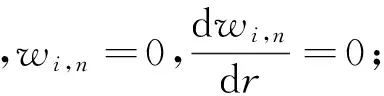
wi,n(r)=ΔNxi,nGi(r)

(17)

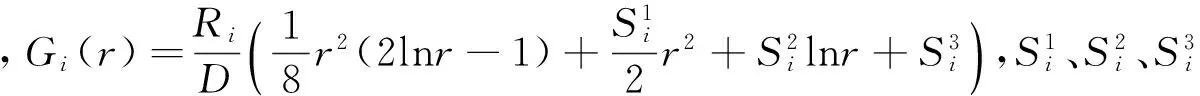
转角αi,n(r)为

(18)

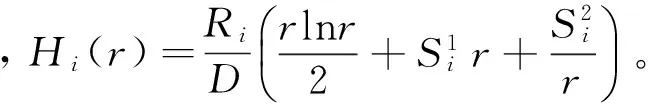
当j≤i时,由ΔNxj,n引起第i层光缆对应端板位置的挠度为

(19)

当j>i时,由ΔNxj,n引起第i层光缆对应端板位置的挠度为

w″j,i=wj,n(Ri)

(20)

由(19)式和(20)式,可得缠绕第n层时第i层光缆对应端板位置的弯曲变形为

(21)

1.3 光缆线包缠绕过程力学模型

忽略芯轴的径向变形,第n层缠绕时第i层光缆的径向变形导致该层光缆内张力的减小,即

(22)

式中,Ex为光缆轴向弹性模量,Ax为光缆截面面积。

假设在各层缠绕时,每层光缆均与端板接触,即每层光缆沿线包轴向变形应等于两侧端板对应该层光缆位置的变形之和,即

(23)

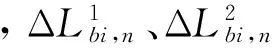
(23)式是在每层光缆均不与端板脱开的假设条件下得出的,而随着光缆的缠绕,内层光缆的轴向挤压力不断增大,可能使端板对应外层光缆位置的变形大于光缆的轴向变形,因此在仿真计算时应判断各层挤压力增量和是否为负值(即该层端板变形是否大于光缆层轴向变形),若为负值,则应忽略该层轴向力增量影响并重新计算。

将(22)式和(23)式联立,即可获得缠绕第n层光缆时内部各层光缆内张力减小量以及各层光缆匝间轴向挤压力增加量。

第i层光缆后续层的缠绕均会造成第i层光缆内张力的减小,缠绕第n层光缆后,第i层光缆内张力为

(24)

光缆内张力引起的光缆轴向应变为

%

(25)

缠绕第n层光缆后,第i层光缆所受外层光缆的压强为

(26)

2 仿真分析

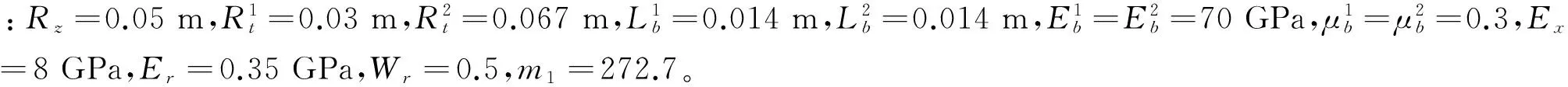
2.1 光缆内部应变分布

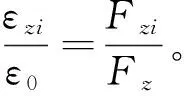
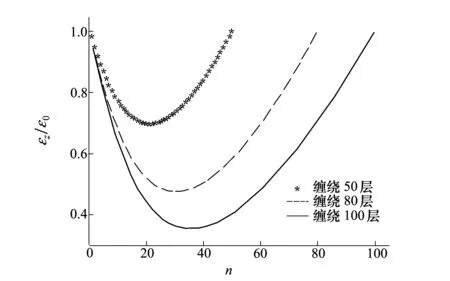
图5 光缆内部应变分布随缠绕层数的变化情况

2.2 光缆层压强

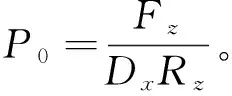
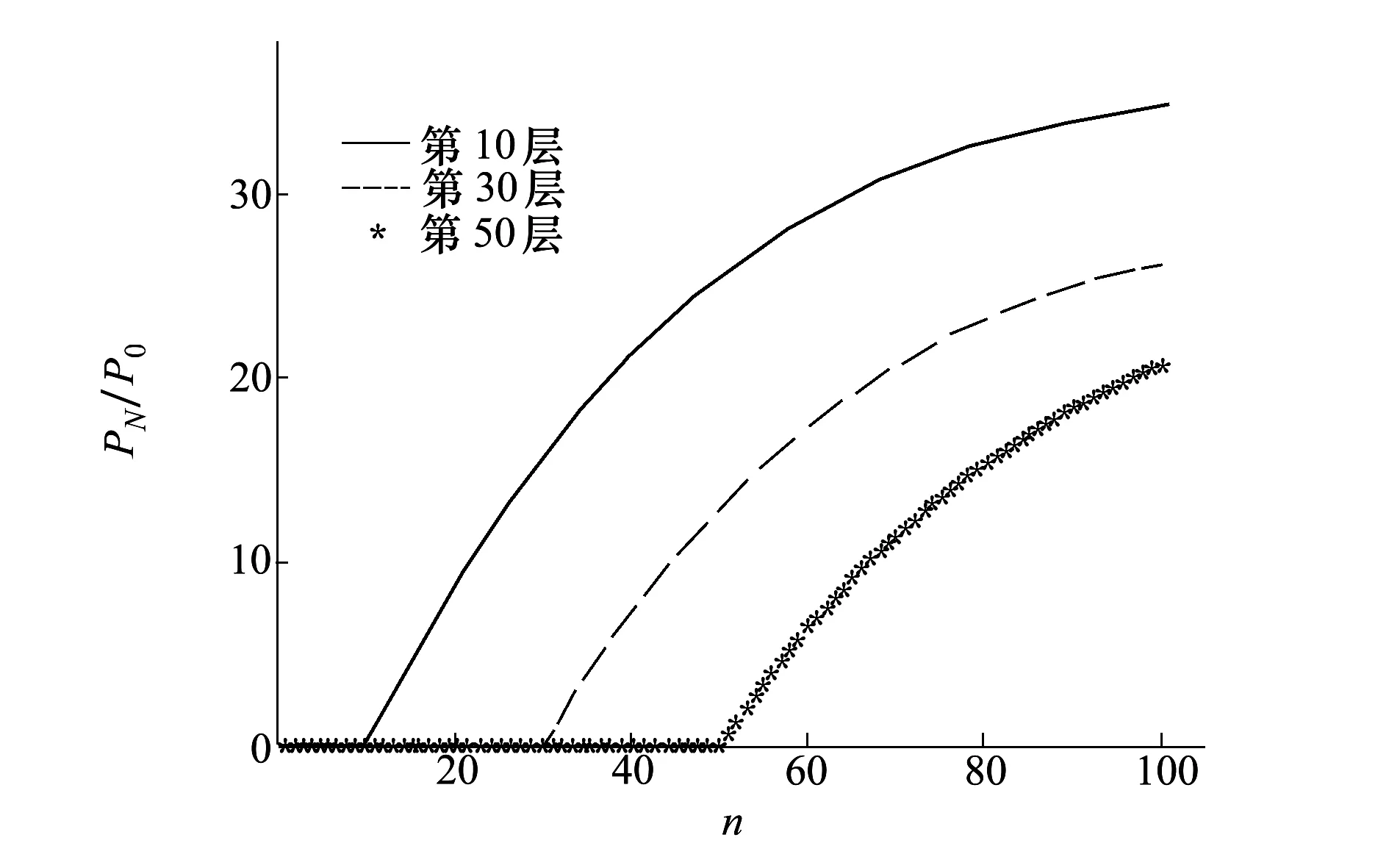
图6 光缆层压强随缠绕层数的变化情况

2.3 端板变形

设两侧端板外圆直径均为300 mm,对两侧端板外圆间距变化进行仿真(如图7a)所示),两侧端板间距随缠绕层数的增加而不断增大,并逐渐趋于平稳。由于仿真采用的是铝基体端板,弹性模量较大,光缆缠绕过程各层光缆对端板施加的轴向挤压力引起的端板变形较小,最大端板间距变化量仅为0.012 6 mm,对去掉芯轴后的光缆线包性能影响较小。水下航行器由于自身总体性能的需求,要求光缆线包重量要轻,以非金属替代金属作为端板材料可有效降低光缆线包的重量,然而非金属材料弹性模量一般远小于金属材料,在相同结构尺寸下以非金属作为端板材料会导致缠绕过程端板变形较大(如图7b)所示,最大端板间距变化量达到了1.35 mm),从而降低光缆线包的布放性能,因此需综合考虑,在保证光缆线包性能的前提下合理选择轻质端板材料。

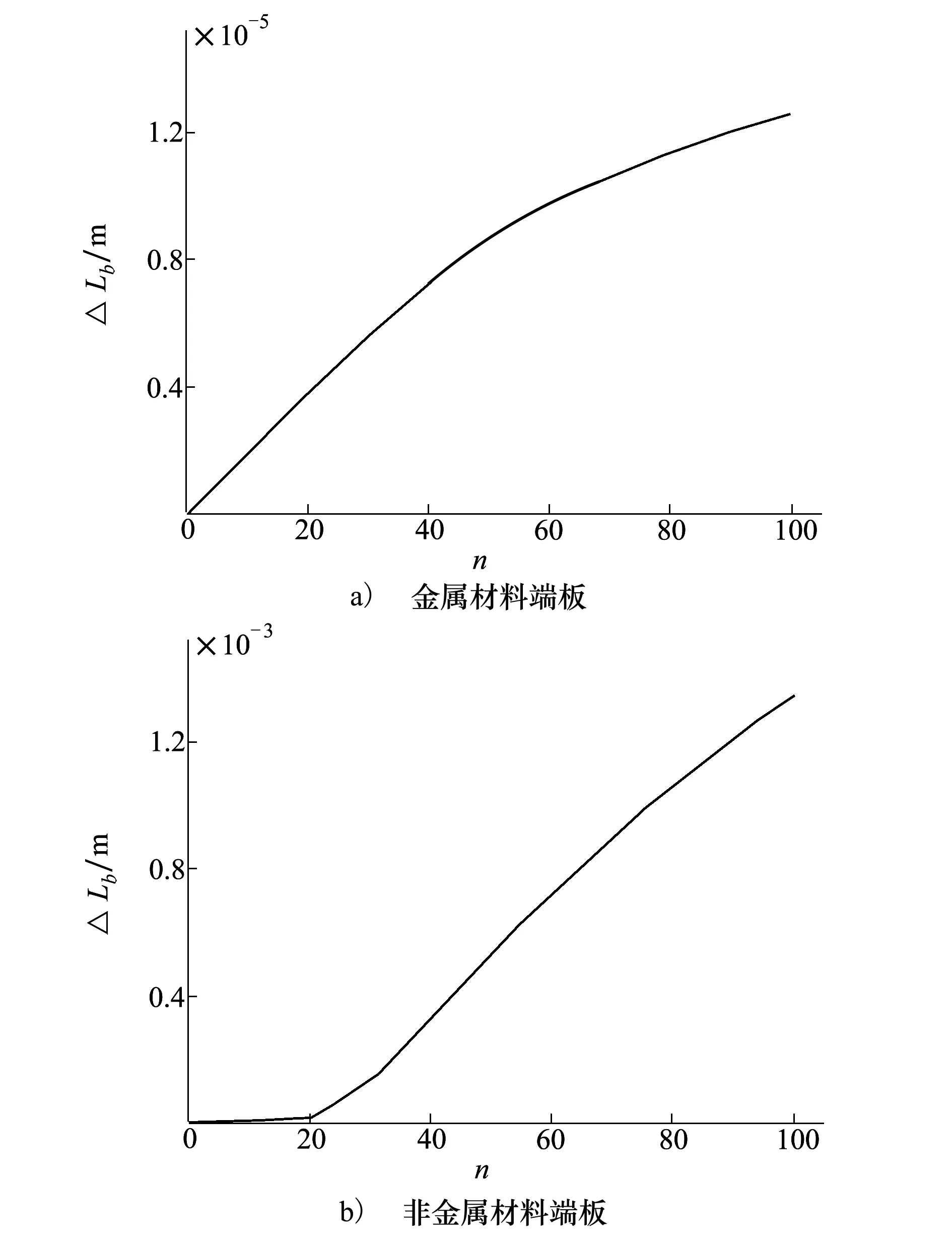
图7 两侧端板间距变化与缠绕层数的关系

3 实验验证

实验使用不同长度的2根光缆以等张力缠绕2个结构尺寸不同的光缆线包,采用AQ8603光纤应变分析仪测量光缆线包缠绕后的内部应变分布。光纤应变分析仪基于布里渊后向散射光检测技术,通过采样一定长度上的布里渊散射频率漂移,获得光纤应变分布数据。缠绕前应测量光缆内光纤的初始应变εs,2个线包分别缠绕了89层和105层。图8为光纤应变分析仪测量的2个光缆线包缠绕后的应变曲线,是应变随长度的变化关系,为对应模型中应变随缠绕层数的变化,将此应变测试数据用公式(27)转化为层均应变。

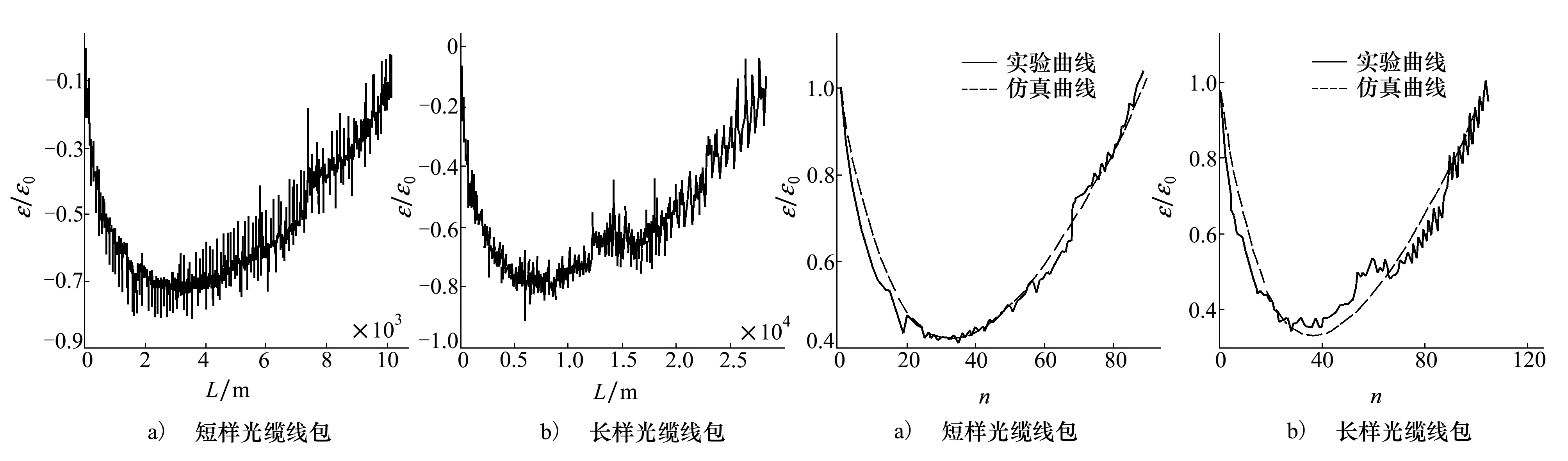
图8 光缆线包缠绕后的应变测试曲线图9 光缆线包内部应变仿真、实验曲线对比

(27)

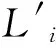
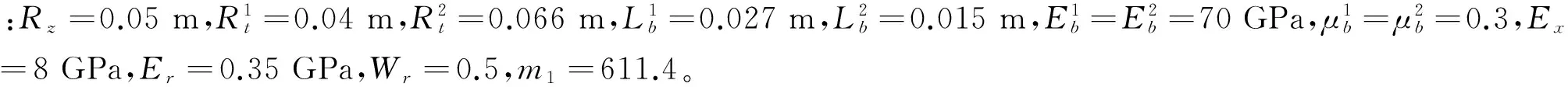
4 结 论

通过对水下航行器光缆线包光缆及端板受力进行理论分析,采用逐层分析各层光缆径向变形和轴向变形的方法建立光缆线包缠绕力学模型,以此模型对光缆线包内部应变分布、光缆层压强以及端板变形随缠绕层数的变化情况进行了仿真分析,利用高精度光纤应变分析仪测量光缆线包的应变,并对实测数据与仿真结果的偏差进行了分析,研究表明,实测与仿真曲线整体趋势一致且偏差较小,模型准确度高。本研究为水下航行器用光缆线包缠绕工艺及缠绕机构设计奠定了理论基础,也可为其他领域光缆线包缠绕过程分析提供借鉴和参考。

[1] 王宝珠,邓宏林,李小瑞,等. 制导光缆中光纤寿命预期[J]. 应用光学,2006,26(6):41-45 Wang Baozhu, Deng Honglin, Li Xiaorui, et al. Lifetime Prediction for the Optical Fiber in Guidance Optical Fiber[J]. Journal of Applied Optics,2006,26(6):41-45 (in Chinese)

[2] 邢静忠,陈利,孙颖. 纤维缠绕厚壁柱形压力容器的应力和变形[J]. 固体火箭技术,2009,32(6):680-689 Xing Jingzhong, Chen Li, Sun Ying. Stress and Deformation of Filament-Wound Thick-Wall Cylinder Pressure Vessels[J]. Journal of Solid Rocket Technology, 2009, 32(6): 680-689 (in Chinese)

[3] Menshykova M, Guz I A. Stress Analysis of Layered Thick-Walled Composite Pipes Subjected To Bending Loading[J]. International Journal of Mechanical Sciences,2014,88:289-299

[4] Zu Lei, Wang Jihui, Li Shuxin. Analysis of Multi-Layered Thick-Walled Filament Wound Hydrogen Storage Vessels[J]. International Journal of Hydrogen Energy, 2014, 39: 21083-21096

[5] Xing Jingzhong, Geng Pei, Yang Tao. Stress and Deformation of Multiple Winding Angle Hybrid Filament-Wound Thick Cylinder under Axial Loading and Internal And External Pressure[J]. Composite Structures,2015,131:868-877

[6] 刘成旭,邢静忠,陈利,等. 柔性厚壁筒环向缠绕张力分析与设计[J]. 固体火箭技术,2013,36(2):261-265 Liu Chengxu, Xing Jingzhong, Chen Li, et al. Analysis of Residual Winding Tension and Design of Winding Tension for Loop Winding on Flexible Cylinder[J]. Journal of Solid Rocket Technology,2013,36(2):261-265 (in Chinese)

[7] 梁清波,邢静忠,杨涛. 柱形缠绕件的环向缠绕张力设计的理论研究及其数值模拟[J]. 固体火箭技术,2013,36(6):799-835 Liang Qingbo, Xing Jingzhong, Yang Tao. Theoretical Research And Numerical Simulation of Winding Tension Design of Hoop Winding on Cylindrical Mandrel[J]. Journal of Solid Rocket Technology,2013,36(6):799-835 (in Chinese)

[8] 邢静忠,梁清波,刘成旭,等. 圆柱形厚壁缠绕件的环向缠绕张力分析的逐层叠加法[J]. 固体火箭技术,2015,38(2): 261-272 Xing Jingzhong, Liang Qingbo, Liu Chengxu, et al. Analysis of Winding Tension for Hoop Winding on Deformable Thick-Walled Cylinder with Superposition by Layers[J]. Journal of Solid Rocket Technology,2015,38(2):261-272 (in Chinese)

[9] 胡勇,许学三,胡吉全. 基于MATLAB的双折线式多层缠绕卷筒的受力分析研究[J]. 武汉理工大学学报(交通科学与工程版),2015,39(2):297-300 Hu Yong, Xu Xuesan, Hu Jiquan. Force Analysis of Lebus Drum Wound by Multi-Layer Wire Rope Based on MATLAB[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering),2015,39(2):297-300 (in Chinese)

[10] 马成举,任立勇,唐峰,等. 基于分布式光纤Bragg光栅传感技术的光缆卷盘静态压力研究[J]. 物理学报,2012,61(5):1-6 Mu Chengju, Ren Liyong, Tang Feng, et al. Study on Static Pressure of Fiber Cable Spool Based on Distributed Fiber Bragg Grating Sensing Technology[J]. Acta Physica Sinica,2012,61(5): 1-6 (in Chinese)

[11] S.铁摩辛柯,S. 沃诺斯基.板壳理论[M]. 北京:科学出版社,1977:55 S.Timoshenko, S. Woinowsky-Krieger. Theory of Plates and Shells[M]. Beijing, Science Press,1977:55 (in Chinese)

Winding Mechanical Modeling and Simulation of Fiber Optic Cable Spool for Underwater Communication

Tang Weijiang1,2, Liu Weidong1,3, Chen Gang2, Yang Heran2, Zhang Jianjun1

1.School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China 2.The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710077, China 3. Science and Technology on Underwater Information and Control Laboratory,Northwestern Polytechnical University, Xi′an 710072, China

Underwater high-capacity and long-distance communication relies on fiber optic cable and other wired communication methods, because electromagnetic wave can′t propagate in water. Thus, optimizing the design of winding technology and winding mechanism is very important for reducing the probability of communication failure and improving the reliability of underwater communication, especially in the field of underwater vehicles, which releasing the fiber optic cable during the movement of vehicles. A layer-by-layer analysis method which adopts the radial deformation and axial deformation of each cable layer as increments is proposed, and a winding mechanical model of fiber optic cable spool is established on the basis of the mechanical analysis of the cable winding process and the end plate. The model reveals the inherent law of inner tension distribution and end-plate deformation in winding process. The simulations of inner strain and layer pressure and end-plate deformation are carried out, which adopt the parameters of spool structure and winding technology. It is shown that the simulation results of inner strain are consistent with experimental data through comparative analyses.

underwater vehicle, fiber optic cable spool, winding mechanical model, cable axial strain, end-plate deformation

2016-04-18

国家自然科学基金(61473224)资助

汤伟江(1979—)，西北工业大学博士研究生，主要从事水下有线通信技术研究。

TN91

A

1000-2758(2016)06-0996-08