高超声速飞行器机动飞行受限控制方法研究

杜昊昱, 凡永华, 闫杰

(西北工业大学 航天学院, 陕西 西安 710072)

高超声速飞行器机动飞行受限控制方法研究

杜昊昱, 凡永华, 闫杰

(西北工业大学 航天学院, 陕西 西安 710072)

吸气式高超声速飞行器飞行过程中舵偏不能过大，攻角、角速率等飞行状态必须满足约束，这既是超燃冲压发动机工作条件的要求，也是为了减小飞行器状态散布。针对吸气式高超声速飞行器进行高度控制时，飞行器状态和舵偏必须满足约束的实际问题，引入指令调节器进行高度回路设计。基于PI+LQ方法设计过载控制器，利用高度回路的比例-微分产生过载信号，过载信号经过指令调节器生成调节指令，过载控制器跟踪该指令完成高度跟踪。仿真结果表明，该方法设计的控制系统在阵风干扰情况下能够满足状态约束并实现快速跟踪。

指令调节器;状态约束;受限控制;模型预测控制;最优控制

吸气式高超声速飞行器是指以超燃冲压发动机为动力，在大气层内实现飞行速度大于5倍音速的飞行器。超燃冲压发动机性能同马赫、高度、飞行姿态密切相关，且发动机余量较小，对飞行控制造成了硬性约束。该飞行器控制系统的任务是控制飞行器飞行状态，使其满足超燃冲压发动机的工作条件，同时快速跟踪指令信号。长航时高超声速飞行器飞行轨迹大致可分为助推爬升段、转弯调整段、巡航飞行段以及下滑飞行段[1]，其中助推爬升段和转弯调整段可按照基准弹道进行轨迹控制，而巡航飞行段纵向采用高度控制。巡航飞行段飞行器可以实现一定程度的机动，但如果要求飞行器快速机动，如依阶跃高度指令迅速爬升时，则可能导致飞行器状态超出约束，或舵偏饱和，使得控制性能变差，甚至造成发动机无法工作。因此，高超声速飞行器快速机动时，如何协调飞行状态及舵偏的约束与实现快速指令跟踪是一个急需解决的问题。

针对上述问题，国内外的专家学者在高超声速飞行器控制系统设计方面做出了大量研究：文献[2]中，Michael等人利用参考调节器解决了高超声速飞行器燃油当量比及舵偏受约束情况下的高度及速度跟踪问题。Andrea Serrani等人在文献[3]中提出自适应制导控制方法防止了高超声速飞行器制导过程中舵偏饱和。Zinnecker等人在文献[4]中针对高超声速飞行器滑翔器设计了一个指令调节器配合自适应控制器跟踪参考信号，避免了执行机构饱和且防止了阵风饱和。但都没有考虑受发动机工作条件限制所必需满足的飞行状态(如攻角、俯仰角速率)约束。

Petersen Christoper等人在文献[5]中，利用了拓展指令调节器结合预测制导设计了高超声速飞行器无动力滑翔段的制导控制问题，使得该飞行器能够避障的同时满足飞行状态约束，取得了良好的效果。但与滑翔段制导控制不同，中制导段因发动机工作使得飞行状态将受到更为严格的约束，同时，飞行器跟踪预先指定的极小的航迹角(文中取-1°)方案与飞行器在中制导段快速机动的要求不符。文献[6]使用自适应控制方法完成了飞行器在飞行状态及舵偏约束条件下的指令跟踪，但其高度指令不能显式表达，且不能实现快速机动。

针对长航时吸气式高超声速飞行器必须对飞行状态和舵偏进行约束，同时实现快速机动的控制问题，上述文献或未能充分考虑飞行状态约束，或不能实现快速机动，为此有必要引入新的控制方案。本文提出LQ过载控制器和CG指令调节器相结合的方法进行设计，考虑飞行状态和舵偏约束，同时满足飞行器快速机动的要求。

1 模型描述及控制器结构

1.1 高超声速飞行器建模及风干扰模型

采用文献[1]的高超声速飞行器模型数据，该飞行器采用近似轴对称结构外形，如图1所示。

图1 轴对称外形的高超声速飞行器示意图

吸气式高超声速飞行器是指以超燃冲压发动机为动力,在大气层内实现飞行速度大于5高超声速飞行器攻角α、俯仰角速率q、以及舵偏角δe的取值范围:a∈[-2°,8°]、q∈[-10°/s,10°/s]、δe∈[-20°,20°]。

高超声速飞行器纵向运动刚体方程如下

(1)

式中,Iy为飞行器绕弹体y轴的转动惯量,q为俯仰角速度。各项气动力和力矩由以下关系描述:

临近空间飞行器大气风场模型主要由平均风模型、阵风模型和切变风模型组成。其中阵风干扰对高超声速飞行器控制系统影响最大,该扰动直接影响飞行器在空中的飞行过程。目前工程上常用的是全波长“1-cosine”离散阵风模型。

(2)

式中,W为飞行位置y上所对应的阵风速度;Wmax为阵风的幅值;dm为阵风层的厚度,也被称为阵风尺度。取25 km高度,阵风尺度为60 m风场模型,得到该风场条件下阵风幅值为:垂直9 m/s。由于高超声速飞行器机动时速度极大,攻角较小,所以水平方向突风对飞行器影响可忽略不计。由阵风引起的附加风攻角可以简化为W/V。

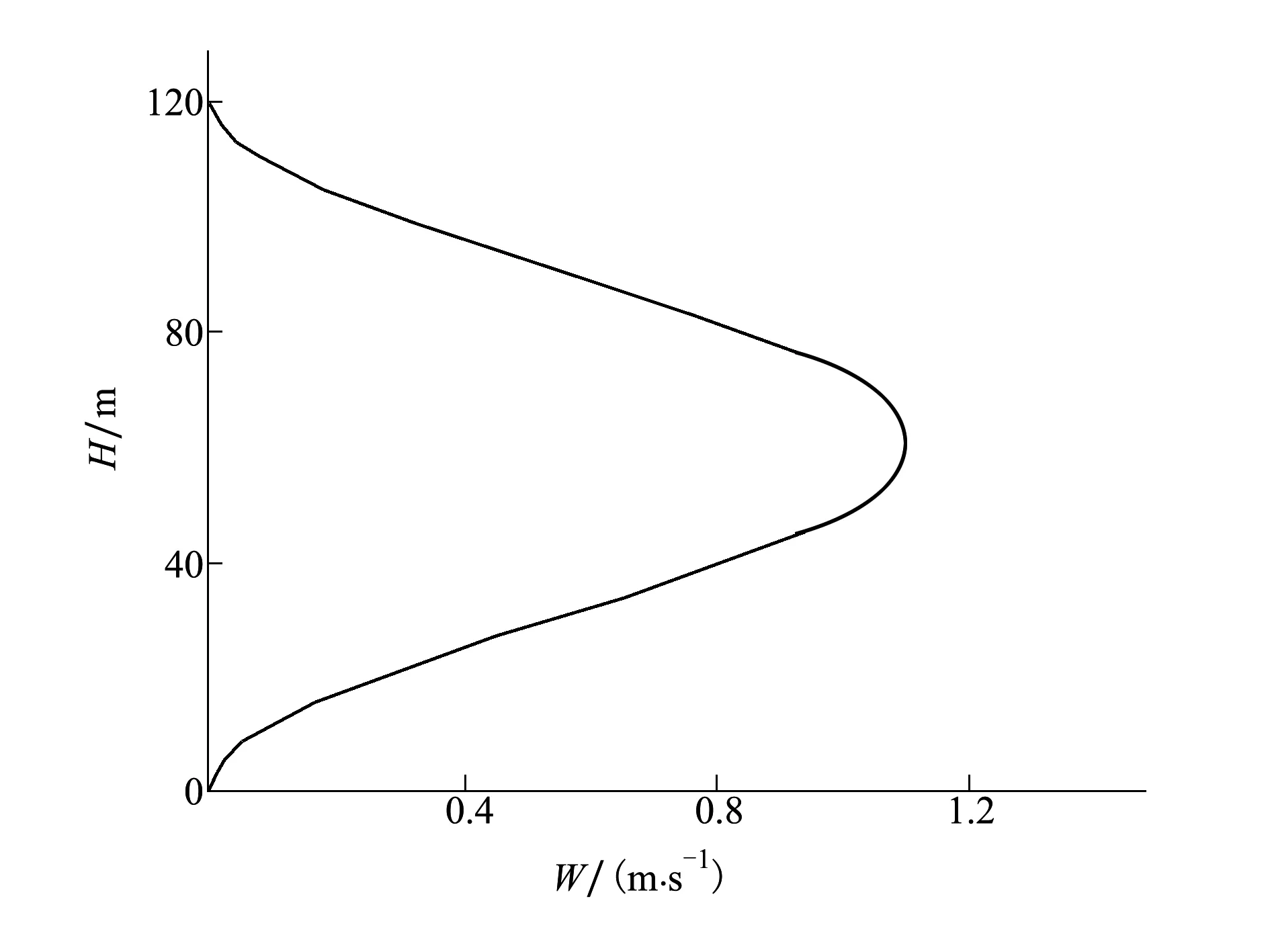
图2 “1-cosine”纵向突风模型

1.2 传统高度控制器设计

高度控制器设计分为2层,内层使用LQ设计纵向过载控制器,外层使用高度比例加微分控制(PD)生成高度误差信号形成过载指令。对方程(1)应用小扰动线性化方法,得到飞行器动力学的状态空间描述,再利用LQ最优控制方法设计高超声速飞行器纵向过载控制系统。该系统采用最优多变量比例加积分反馈控制器完成[7]。

考虑高超声速飞行器的小扰动线性化状态空间方程为:

y=CPxP

(3)

式中,状态向量xP=[α,q],控制向量up=[δe],y=ny(t)假设系统的状态向量完全可测。

为了实现零稳态跟踪误差,根据内模原理,考虑在反馈控制系统中加入积分环节,并且利用LQR最优控制设计方法来求取最优反馈增益以及积分增益。定义跟踪误差为

e1(t)=r(t)-y(t)

(4)

式中,r=[hC(t)]为参考指令信号。积分器的输出定义为:

(5)

将(2)式与(4)式联立,一起构造误差增广系统如下

(6)

(7)

式中,各个矩阵的定义分别为:

增广系统误差向量可以定义为:

e=[r-CPxp]=Mx+Nr

(8)

(9)

因为控制器设计的目标是实现对飞行器纵向过载指令的跟踪控制,即要求跟踪误差e(t)在控制系统的作用下在有限时间收敛到零。为此根据最优控制理论,提出以下线性二次型指标函数:

(10)

式中,误差加权矩阵Q对称正定,控制量加权矩阵R对称正定。通过求解代数黎卡提方程,得到最优控制律u*=KPxp+Kww,系数由黎卡提方程的解得到。

高超声速飞行器纵向运动LQ最优跟踪控制系统结构图如图3所示:

图3 高超声速飞行器纵向运动控制系统结构图

2 指令调节器(CG)设计

指令调节器可以实时检测系统状态和控制输入,将系统状态、控制输入等约束作为设计约束在设计阶段予以充分考虑。指令调节器于文献[7]中首次提出,文献[8]将其用于飞行器的姿态控制,增强了飞行器的安全性、提升了舒适性。本文所使用CG结构如图4所示。

图4 指令调节器结构

(11)

系统满足以下条件:

1) 系统(11)是一个渐进稳定系统。

2) 系统(11)是无偏的。即

Hy(I-Φ)-1G=Im。

(12)

CG在每一个当前时刻t,找到一个指令g(t)是当前状态x(t)和参考信号r(t)的函数,使得g(t)是r(t)在约束下的最佳近似。记作:

(13)

(14)

在不考虑扰动的情况下,一个足够小的常数δ>0,构成集合:

Cδ:=C～Bδ

(15)

式中,Bδ是一个以δ为半径,以原点为圆心的球域。特别地,我们假设wδ是所有稳态解满足约束并具有裕度δ。CG在每一个当前时刻选取一个指令v(·)≡w,满足w∈wδ,使得过程动态演化满足约束且有限时间收敛,并满足指令w与参考指令r距离最小,并实施这个指令。在下一个时间周期,获取新测量的状态后重复上述步骤。定义集合v(x)如下:

∀k∈Z+}

(16)

(17)

(18)

式中,Ψ是正定对称矩阵。本文中取Ψ为单位阵。

3 仿真结果及分析

为了验证上述CG调节器对高超声速飞行器的有效性,利用该方法对高超声速飞行器进行高度指令跟踪控制仿真分析。取飞行器的初始状态[1]为:

状态名称状态值速度V0/(m·s-1)1795高度H0/m25000攻角α0(°)2.0俯仰角速率q/((°)·s-1)0

飞行器控制系统结构如图5所示，对比加入CG和没有CG的控制系统进行仿真，爬升高度100 m。

图5 高超声速飞行器纵向运动CG+LQ控制系统结构图

仿真结果如下：

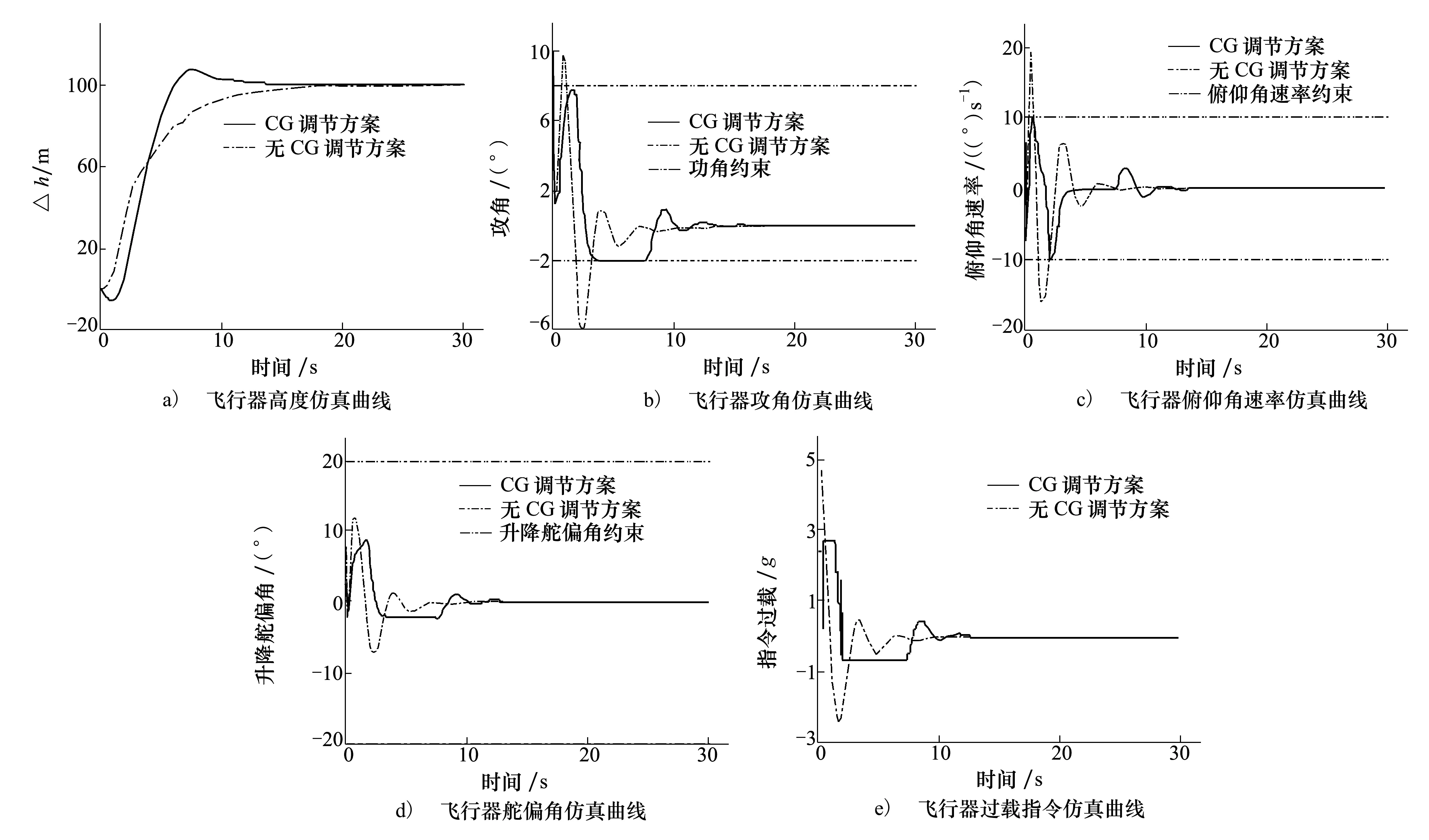
图6 仿真结果对比图

由仿真结果可以看出，没有CG调节器的系统攻角和俯仰角速率都明显超出了约束，舵偏虽然没有超出约束，但是舵偏变化较为剧烈。经过CG调节的参考指令信号较无CG调节的平缓，飞行器攻角保持在-2°～7.15°之间，俯仰角速率保持在-10°～10°/s之间，舵偏保持在-2.2°～8.4°之间。2种方案飞行器高度最终都能收敛到指令高度，区别在于经过CG调节的系统由于受飞行状态的限制前期上升较无CG系统慢，后期较无CG系统快，并产生0.73%的超调。无CG调节的系统调节时间10.95 s，有CG调节的调节时间为5.47s。由结果可知，CG调节器能够有效地调节指令，使飞行器实现快速轨迹跟踪且满足各项指标约束。

4 结 论

本文提出的方案针对高超声速飞行器飞行状态和舵偏约束情况下实现快速机动的问题，取得了良好的控制效果。但CG调节器的引入大大增加了飞控系统的运算量，难以实时应用，其算法只有经过简化或加以改进才能真正用于飞行控制，如何获取更加快速的飞行控制指令调节器将是后续研究的重点。

[1] 闫杰，于云峰，凡永华. 吸气式高超声速飞行器控制技术[M]. 西安：西北工业大学出版社，2014

[2] Michael A Bolender, David B Doman. Combined Reference Governor and Anti-Windup Design for Constrained Hypersonic Vehicle Models[C]∥AIAA Guidance,Navigation and Control Conference,2009: 10-13

[3] Serrani A, Zinnecker A M, Fiorentini L, et al. Integrated Adaptive Guidance and Control of Constrained Nonlinear Air-Breathing Hypersonic Vehicle Models[C]∥American Control Conference, 2009: 3172-3177

[4] Zinnecker A, Serrani A, Bolender M, Doman D. Combined Reference Governor and Anti-Windup Design for Constrained Hypersonic Vehicles Models[C]∥AIAA Guidance, Navigation, and Control Conference, 2009: 2009-6283

[5] Christoper Petersen, Morgan Baldwin, Kolmanovsky. Model Predictive Control Guidance with Extended Command Governor Inner-Loop Flight Control for Hypersonic Vehicles[J]. Guidance, Navigation and Control and Co-Located Conferences, 2013: 19-22

[6] Fiorentini L, Serrani A. Adaptive Restricted Trajectory Tracking for a Non-Minimum Phase Hypersonic Vehicle Model[J]. Automatica, 2012, 48(7): 1248-1261

[7] Kapasouris P, Athans M, Stein G. Design of Feedback Control Systems for Unstable Plants with Saturating Actuators[J]. IEEE Confernce on Decision & Control, 1988: 469-479

[8] Famularo D, Martino D, Mattei M. Constrained Control Strategies to Improve Safety and Comfort on Aircraft[J]. Journal of Guidance Control & Dynamics, 2012, 31(6): 1782-1792

A Novel Method for Hypersonic Flight Vehicle′s Maneuver Flight Constrained Control

Du Haoyu, Fan Yonghua, Yan Jie

(School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China)

An air-breathing hypersonic flight vehicle requires that its elevator deflection should not be too large and that such flight states as angle of attack and angular velocity must satisfy certain constraints to meet the working conditions of scramjet engine and to reduce the state diffusion of the flight vehicle. Therefore, we proposed the above-mentioned control method based on the model predictive control principles and designed two separate controllers: a traditional linear controller that guarantees the tracking of the altitude of the hypersonic flight vehicle in the absence of constraints and a command governor, a nonlinear static device that must modify the reference signals of normal acceleration to meet the constraints imposed by actuators and flight vehicle. The simulation results show that under the interference of gust, our method can effectively fast track maneuver commands, control the altitude of the hypersonic flight vehicle and satisfy its elevator deflection and flight state constraints.

angle of attack, angular velocity, flight control systems, hypersonic flight vehicles, maneuverability，altitude control, command governor, constrained control, model predictive control, state constraints

2016-09-06

国家自然科学基金(91216104)资助

杜昊昱(1988—)，西北工业大学博士研究生，主要从事飞行器控制研究。

V249.122

A

1000-2758(2016)06-0945-06