基于扩展卡尔曼滤波的高转速修正引信滚转角测量方法

王佳伟, 史凯, 徐国泰, 钱荣朝, 闫杰

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.机电动态控制重点实验室, 陕西 西安 710065)

基于扩展卡尔曼滤波的高转速修正引信滚转角测量方法

王佳伟1,2, 史凯2, 徐国泰2, 钱荣朝2, 闫杰1

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.机电动态控制重点实验室, 陕西 西安 710065)

针对二维弹道修正技术中采用双旋稳定弹总体设计方案的修正引信在全弹道范围内的旋转特点，提出了一种基于扩展卡尔曼滤波的高转速修正引信滚转角测量方法。以某双旋稳定迫弹为仿真平台，建立了7自由度(DOF)外弹道仿真模型分析修正引信的旋转特性，完成了滚转角与弹载陀螺输出之间的解析关系推导并验证其正确性；在引入陀螺固有系统误差、测量误差以及北斗卫星定位测量误差后，基于扩展卡尔曼滤波估计方法对修正引信滚转角进行实时测量，仿真结果表明：采用该方法1 s内就可以实现滚转角解算快速收敛，全弹道滚转角解算绝对误差不大于6°，在弹道10～40 s段解算绝对误差不大于2°；通过炮射试验的采集数据进行验证，以15～35 s弹道段为例，滚转角解算绝对误差不大于10°，绝对误差的均值为3.9°，可以满足修正系统的滚转角测量精度要求。

二维弹道修正；双旋稳定弹；滚转角测量；扩展卡尔曼滤波

在未来联合作战中，炮兵仍然是实施地面火力覆盖的主体力量和支援配合其他军兵种作战的基本力量，常规炮弹在保持对广阔区域的高水平压制能力的同时，还应具备在复杂环境中对小面积、低成本目标的精确打击能力。二维弹道修正引信是一种实现低成本精确打击的前沿技术，仅通过更换弹道修正引信即可满足大批量库存无控弹药智能化、灵巧化改造的迫切需求，其赋予常规弹药低成本精确打击的能力已经成为世界各国发展弹药引信装备的强烈共识。

基于中大口径迫/榴弹平台，采用惯性器件/卫星定位组合测量弹体姿态/弹道参数，将修正引信与弹体通过解耦结构部件连接构成双旋稳定弹(dual-spin stabilized projectiles)，修正引信头部采用的2对翼面布局分别实现引信的滚转控制和弹道修正所需控制力，这是目前国际上二维弹道修正引信技术中最具代表性的总体设计方案[1-2]。修正引信的实时滚转角作为弹道控制模块的重要输入信息，其准确测量是二维弹道修正技术有待解决的关键技术。滚转角测量的主要方法有：太阳方位辅助测量、磁/卫星定位组合测量以及陀螺/卫星定位组合测量等方法。太阳方位辅助测量受到天气限制，具有较大的应用局限性；磁/卫星定位组合测量方法国内外相关文献较多[3]，算法成熟且运算相对简单，但其缺点在于易受到外界强电磁信号干扰，目前仍处于屏蔽/补偿磁干扰的关键技术突破阶段；陀螺/卫星定位组合测量方法的详细介绍最早于1995年由David J.Lucia提出[4]，近年多有文献进行进一步的阐述，其中Hee Young Park等人继承并改良了David J.Lucia的算法[5-6]，但这些方法都仅限于引信修正阶段几近止旋的微旋状态(3 r/s以内)且转速恒定。然而在实际弹道环境中，修正引信的转速远远大于文献[4-6]所设定的理想情况，因此需要设计一种能够适应较高转速的修正引信滚转角测量方法。

针对该二维弹道修正技术设计方案中修正引信在全弹道范围内的旋转特点，本文建立了双旋稳定迫弹七自由度(7 degree of freedom，以下简称7DOF)外弹道模型用以分析修正引信全弹道旋转特性，通过推导得到修正引信滚转角的力学解析关系，并提出一种基于扩展卡尔曼滤波(extended Kalman filter，以下简称EKF)的高转速修正引信滚转角测量方法。

1 研究基础

1.1 解析法推导

双旋稳定受控弹发射后，北斗卫星定位接收机完成重捕定位，开始弹道轨迹测量并得到弹丸地面系下3个方向的速度分量Vx、Vy、Vz,根据所测速度信息可以计算出弹道倾角θ及弹道偏角ψ,见图1所示。

(1)

(2)

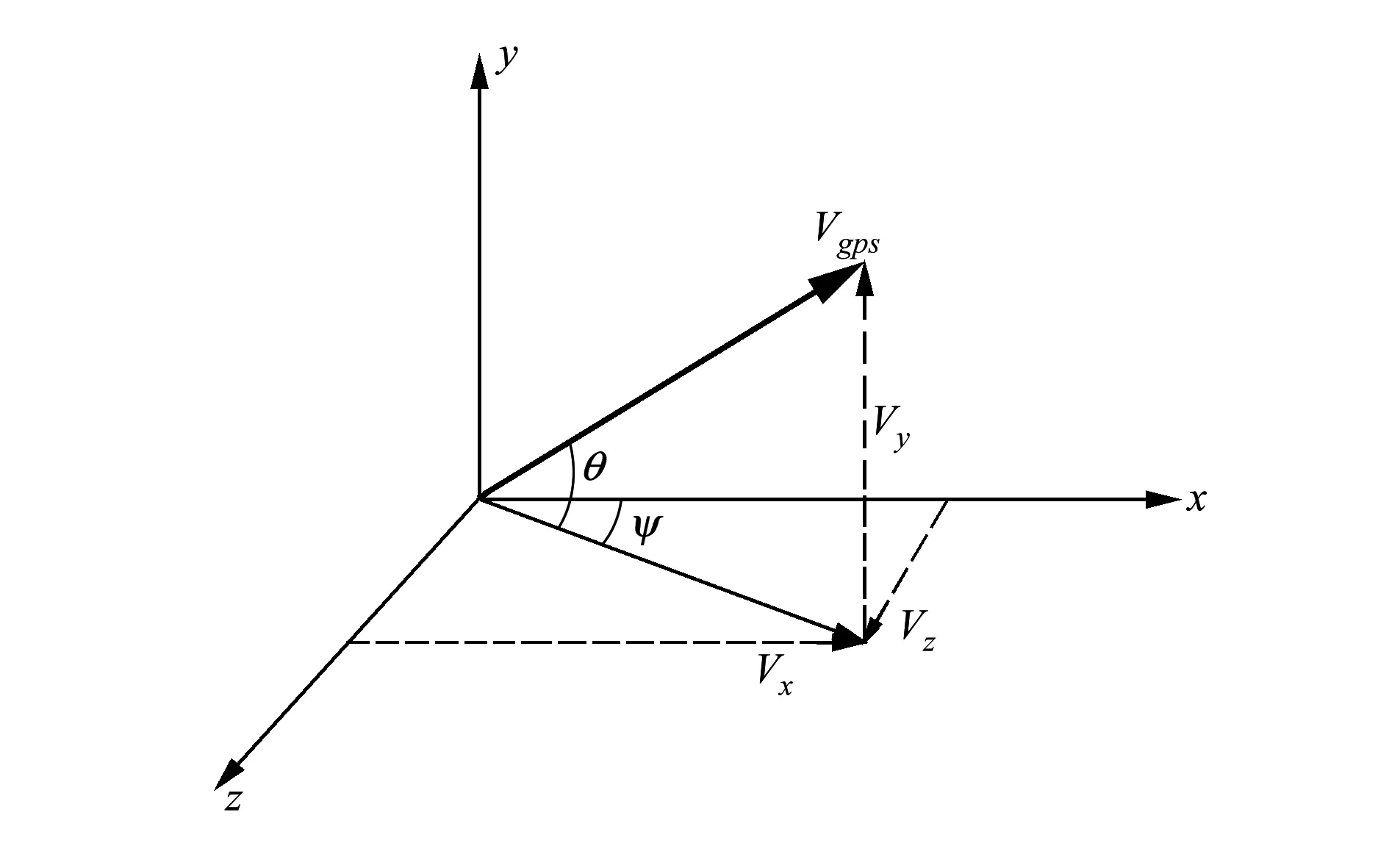
图1 弹道倾角及偏角计算示意图

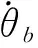
(3)

(4)

式中,θk、θk-1以及ψk、ψk-1分别为相邻采样时刻计算得到的弹道倾角和偏角,th为采样步长。

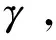
(5)

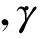
(6)

式中,Lx(θ)为绕Y轴的基本旋转矩阵,联立(5)式可以推导出

(7)

ωxb、ωyb、ωzb即为固连在弹体的三轴陀螺输出,由此建立了滚转角γ与陀螺输出的解析关系,进而可以求得滚转角。

1.2 扩展卡尔曼滤波[8]

卡尔曼滤波器是针对观测状态变量的最优线性滤波器,但对于复杂的非线性系统则需要用到一种非线性滤波方法,而EKF无疑是过去数十年应用最为广泛的非线性状态估计方法。

设k时刻带有离散量测的连续时间系统如下所示

(8)

式中，x为被估计的状态变量,w为协方差为Q的系统噪声,v为协方差为Rk的量测噪声。

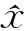
(9)

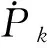
(10)

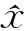
(11)

2 滤波算法设计

根据陀螺输出表达式可以得到滚转角的三角函数表达方程,同时认为陀螺输出由其载体真实角速度及测量误差叠加构成,则有(12)式

(12)

将(12)式改写为

(13)

令估计状态向量Xk包括转速p、初始滚转角γ0以及y/z轴陀螺测量误差,则

(14)

量测向量Zk为

(15)

系统偏微分矩阵见(16)式～(19)式:

式中

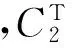
3 仿真验证

3.1 修正引信旋转特性分析

建立某双旋稳定迫弹7DOF外弹道模型,射角采用最大射程角,弹丸初速为名义初速,在炮兵标准气象条件下通过仿真分析修正引信的旋转特性。受控弹全弹道飞行稳定,弹道曲线如图2所示。

图3和图4分别是全弹道范围弹丸和修正引信无控飞行的转速曲线。弹丸发射后,迫弹尾翼产生导转力矩使弹丸转速由静止状态迅速提升至10 r/s左右,之后转速随动压变化(由弹丸速度决定)呈倒“U”型变化趋势且全弹道保持左旋(从弹尾向弹头方向看去);修正引信头部安装与尾翼反向的导转翼面,在反向导转作用下转速迅速提升至25 r/s左右,随后在导转力矩和摩擦力矩的合作用下自由旋转,使其在全弹道内与弹丸旋转方向相反,即向右旋转。

假设北斗卫星定位接收机在10 s内实现重捕定位,那么整个修正阶段的引信转速在15～20 r/s之间波动,远远超过文献[5-6]算法中的转速限制(3 r/s),因此需要设计一种适应较高转速的修正引信滚转角测量方法。

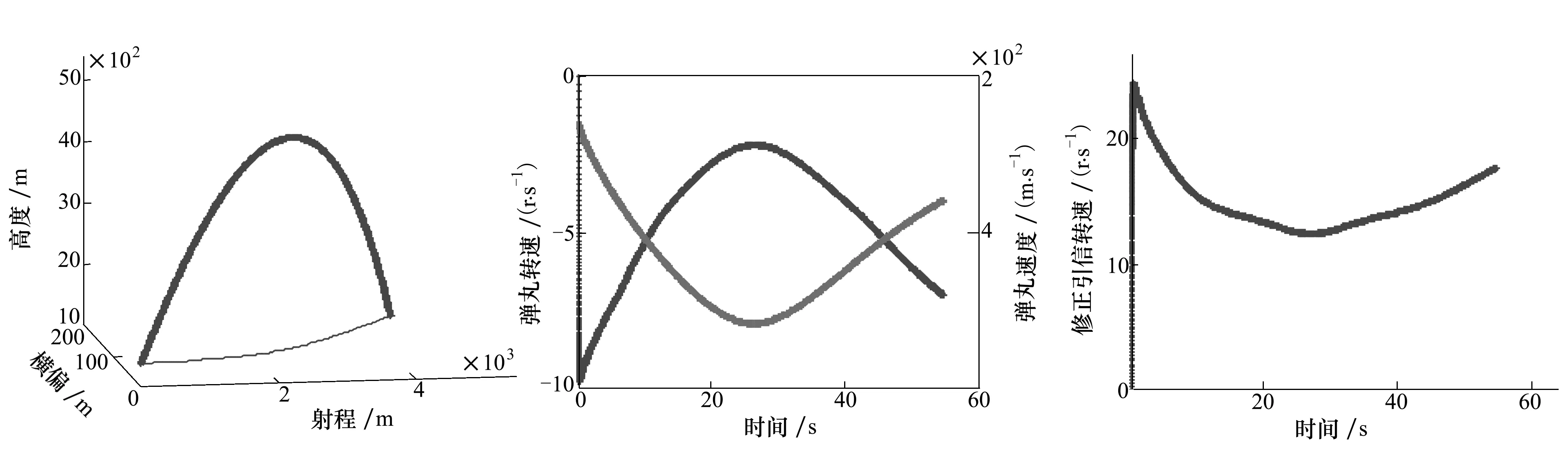
图2 双旋稳定迫弹7DOF外弹道曲线 图3 弹丸转速全弹道变化曲线 图4 修正引信转速全弹道变化曲线

表1给出了应用于滚转角测量模型中的各测量参数。

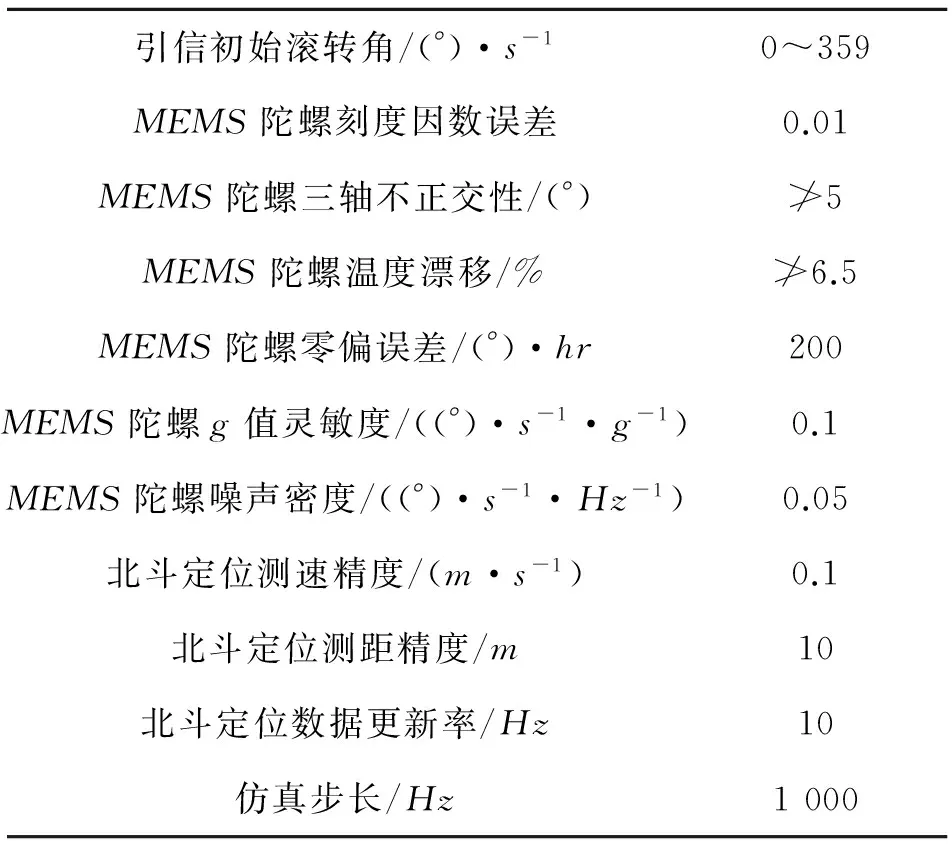
表1 测量模型参数

3.2 理论解析滚转角

在不考虑表1中陀螺固有系统误差、测量误差及北斗定位测量误差的条件下根据理论解析式(7)推导出修正引信实时滚转角，图5是解算滚转角与7DOF模型中修正引信滚转角真值的理论解算绝对误差曲线，可以看到滚转角的解算误差几近为零，这也验证陀螺输出与修正引信滚转角的解析关系推导是正确的。

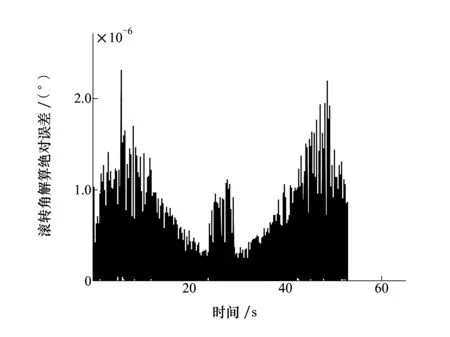
图5 无测量误差条件下的滚转角理论解算绝对误差

然而根据表1引入测量误差后，滚转角真值完全湮没在系统噪声中无法分辨，解算绝对误差如图6所示。可以看到虽然解算误差令人无法接受，但其呈现出弹道初段及末段极大而弹道中段较小的趋势，这是因为修正引信在整个弹道的中段转速最小(几乎为弹道初段和末段的1/2)，由此带来的一个仿真步长周期内的滚转角累积误差也最小。

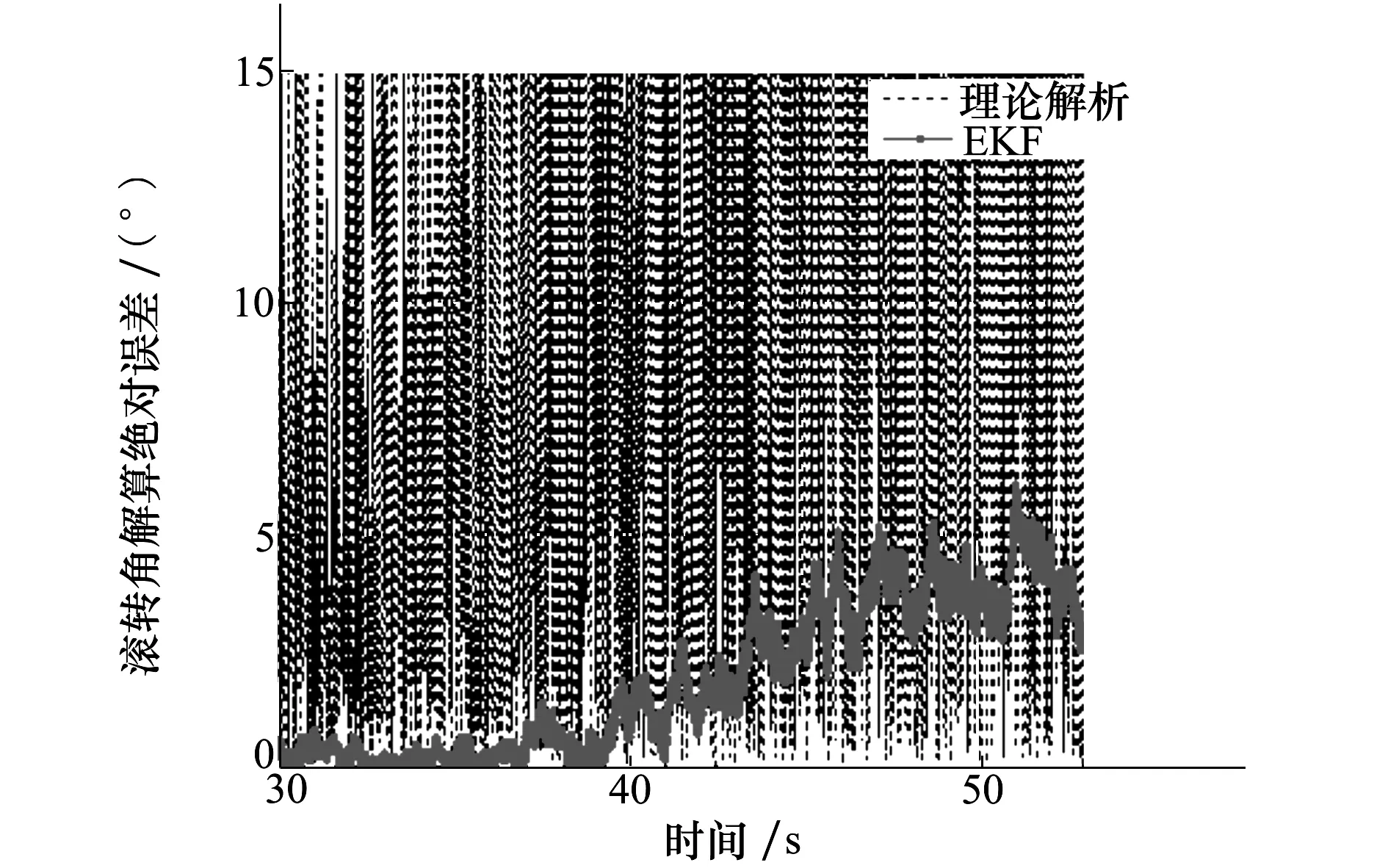
图6 引入测量误差条件下的滚转角解算绝对误差

通过以上仿真可以看到，在引入陀螺和北斗定位测量误差后，仅通过理论推导构建滚转角和陀螺实测输出之间的数学解析关系是无法得到准确滚转角信息的，因此需要采用滤波算法进行优化估计。

3.3 滤波估计滚转角

采用EKF对修正引信滚转角进行优化估计，图7为引入测量误差条件下使用滤波算法前后的滚转角解算绝对误差对比，图8为弹道最后23 s的局部对比图。可以看到采用滤波算法的滚转角估计值与真值之间的误差1 s内快速收敛，收敛后全弹道解算误差不超过6°，其中10～40 s弹道段的解算误差不超过2°。宏观来看，滚转角解算误差在弹道初段及末段有所增大，这是由于该时间段修正引信转速较大而导致每一个仿真步长内滚转角增量过大，预测协方差和滤波器的增益不能随新息同步改变从而失去对突变状态变量的跟踪能力，使估计误差增加。以图4为例，弹道末段修正引信转速超过15 r/s，在一个步长周期内带来的预估状态变量增量就有5.4°，因此采用EKF对修正引信滚转角的估计效果是令人满意的。

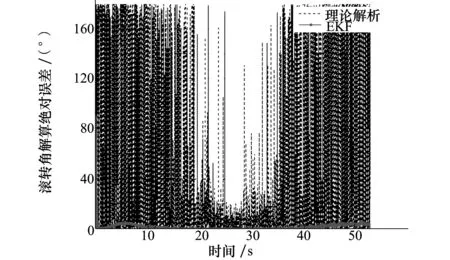
图7 滤波前后的滚转角解算绝对误差对比

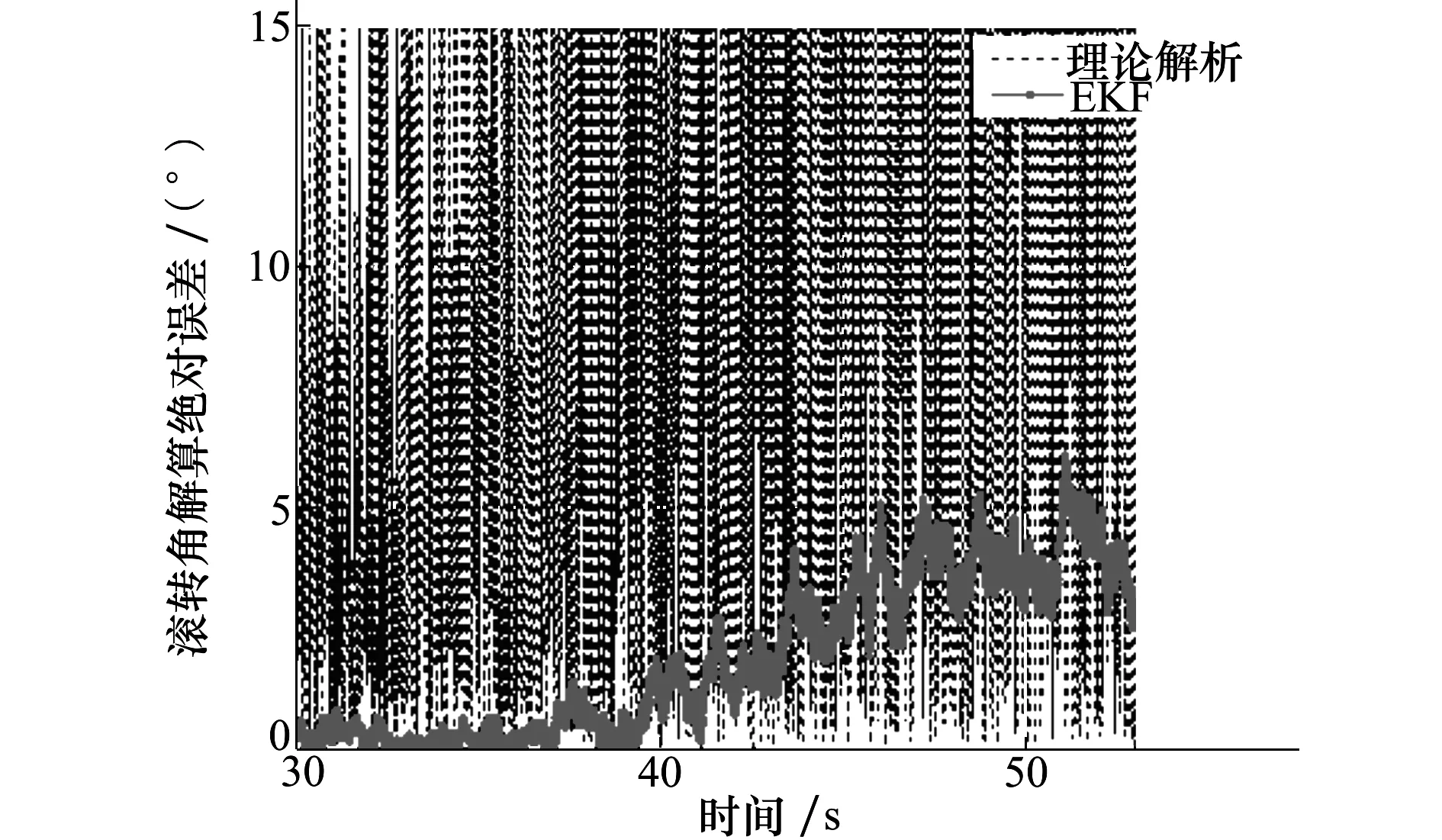
图8 滚转角解算绝对误差对比局部图(最后23 s)

通过减小模型仿真步长降低预估状态变量在一次仿真周期内的增量，可以有效提高滤波估计精度；但是过小的仿真步长会导致仿真数据处理量过大，同时也会在算法移植后大大增加微处理器的运算处理负担，考虑到目前的解算误差满足修正系统精度要求可暂不改变仿真步长。

4 试验验证

配有修正引信的某双旋稳定迫弹采取整体灌封、零部件过载缓冲以及射后上电等工程经验，通过外场炮射试验实测数据来验证滚转角测量算法。利用弹载陀螺试验前的零偏、灵敏度等系统参数标定结果，可以将弹道环境下采集的陀螺输出信号转换为相应角速率，截取15～35 s弹道段陀螺数据以验证滚转角解算算法。陀螺数据如图9所示：

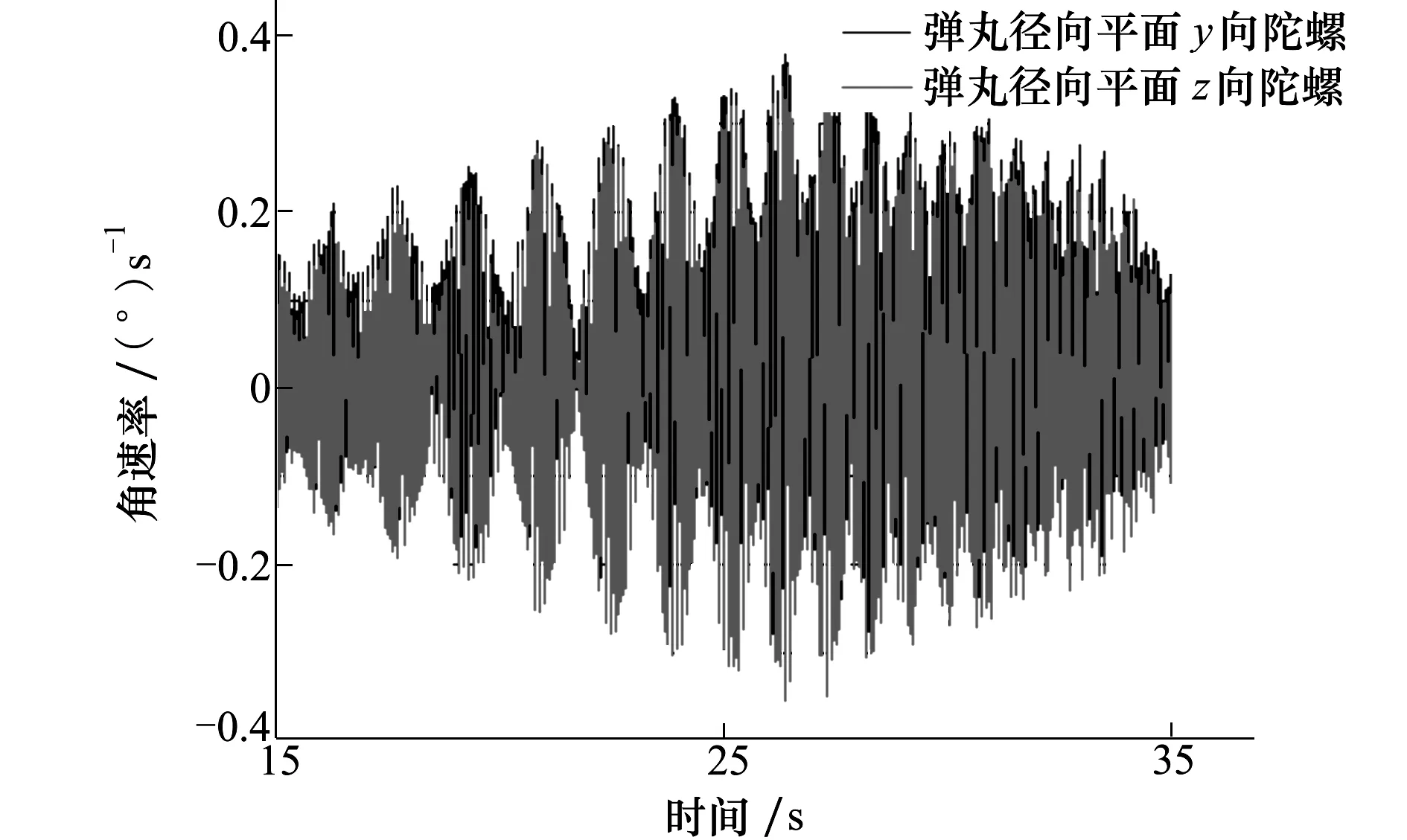
图9 15～35 s弹道段陀螺输出信号

滚转角解算绝对误差如图10所示，经统计：15～35 s弹道段解算绝对误差不大于10°，绝对误差的均值为3.9°，满足滚转角测量指标要求。

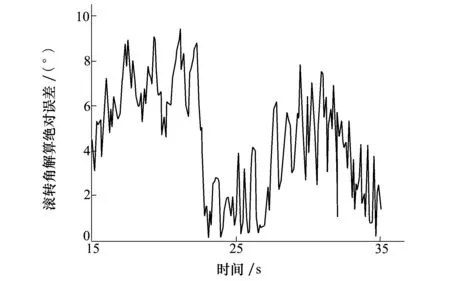
图10 15 s至35 s弹道段滚转角解算绝对误差

5 结 论

本文建立双旋稳定迫弹的7DOF外弹道模型用以分析修正引信在全弹道范围内的转动特性，通过力学推导得到滚转角的理论解析表达式，并仿真验证了其正确性；在此基础上引入了陀螺固有系统误差、测量误差以及北斗卫星定位测量误差后，基于EKF方法估计出修正引信实时滚转角。仿真结果表明：采用该估计方法1 s内就可以实现滚转角解算快速收敛，全弹道滚转角解算绝对误差不大于6°，在弹道10～40 s段解算绝对误差不大于2°；最后通过外场炮射试验采集数据进行验证，以15～35 s弹道段为例，滚转角解算绝对误差不大于10°，绝对误差的均值为3.9°，可以满足修正系统的滚转角测量精度要求。

[1] Philippe Wernert, Stability Analysis for Canard Guided Dual-Spin Stabilized Projectiles[C]∥AIAA Atmospheric Flight Mechanics Conference, 2009

[2] Philippe Wernert, Friedrich Leopold, Denis Bidino, Joseph Juncker. Wind Tunnel Tests and Open-Loop Trajectory Simulations for a 155 mm Canards Guided Spin Stabilized Projectile[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2008

[3] James M Maley. Efficient Attitude Estimation for a Spin-Stabilized Projectile[J]. Journal of Guidance, Control, and Dynamics, 2016, 39: 339-350

[4] Lucia David J. Estimation of the Local Vertical State for a Guided Munition Shell with an Embedded GPS/Micro-Mechanical Inertial Navigation System[D]. MIT, 1995

[5] Hee Young Park, Kwang Jin Kim, JangGyu Lee, ChanGook Park. Roll Angle Estimation for Smart Munition[C]∥IFAC Symposium on Automatic Control in Aerospace, 2007

[6] Lee Han Sung, Kim Kwangjin, Park Hee Young. Roll Estimation of a Smart Munition Using a Magnetometer Based on an Unscented Kalman Filter[C]∥AIAA Guidance Navigation and Control Conference and Exhibit, 2008

[7] 韩子鹏. 弹箭外弹道学[M]. 北京：北京理工大学出版社，2008 Han Zipeng. Exterior Ballistics for Projectiles and Rockets[M]. Beijing, Beijing Institute of Technology Press, 2008 (in Chinese)

[8] 张勇刚，李宁，奔粤阳. 最优状态估计：卡尔曼，H∞及非线性滤波[M]. 北京：国防工业出版社，2013 Zhang Yonggang, Li Ning, Ben Yueyang. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches[M]. Beijing, National Defense Industry Press, 2013 (in Chinese)

Roll Estimation of High Rotation Speed Correction Fuze Based on Extended Kalman Filter

Wang Jiawei1,2, Shi Kai2, Xu Guotai2, Qian Rongzhao2, Yan Jie1

1.School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.Science and Technology on Electromechanical Dynamic Control Laboratory, Xi′an 710065, China

According to the rotating features of correction fuze used on dual-spin stabilized projectile, which is a common designing scheme in 2-D course correction field, a method with Extended Kalman Filter is introduced to solve roll estimation of correction fuze with high rotation speed. Basing on a certain kind of dual spin stabilized mortar projectile, a 7-DOF exterior trajectory model is established to analyse the rotating feature of correcting forward body, and then the analytic formula between roll angle and outputs of gyroscope fixed on fuze is developed and verified. Considering system error of gyroscope, measuring error and BD′s positioning error, the real-time roll estimation method is demonstrated using the Extended Kalman Filter method. Simulation results show that the roll estimation absolute error dramatically decreases within 1 s, which is not larger than 6 degrees in whole exterior trajectory. Furthermore, the absolute error in trajectory between 10 s and 40 s is less than 2 degrees. Finally the estimation algorithm is tested in shooting range, the results show that the absolute estimation error is no more than 10 degrees and the mean value of absolute error is 3.9 degrees, which are especially calculated from 15～35 s in whole trajectory. The accuracy of estimation can fully meet require of roll angle measurement in correcting system.

2-D course correction; dual-spin stabilized projectile; roll estimation; design of experiments; extended Kalman filter

2016-08-20

国家自然科学基金(U1630127)资助

王佳伟(1984—)，西北工业大学博士研究生，主要从事二维弹道修正引信技术研究。

TJ765

A

1000-2758(2016)06-0938-07