基于CART算法的空气质量指数回归预测模型的学习

陈 峰

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

基于CART算法的空气质量指数回归预测模型的学习

陈 峰

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

采用了CART算法结合广义交叉验证(GCV)，对空气质量指数(AQI)预测建立了模型。结果显示，采用广义交叉验证选出的最优回归树能有效的预测空气质量指数。与多元回归方法相比，回归树预测的准确率较高。

CART；空气质量指数；GCV；多元线性回归

分类回归树算法也称为CART(Classificationand Regression tree)算法，由L.Breiman等人于1984年提出，是决策树算法中一种专用于分类与回归的方法，是在给定的输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假设决策树是二叉树，每一个内部节点特征的取值为“是”和“否”。在每一个子节点上，在左边的分支是取值为“是”的分支，在右边的分支是取值为“否”的分支，这样的决策等价于递归地二分每个特征，将输入空间即特征空间划分成有限个单元，并在这些单元上确定预测的概率分布，也就是给定的输入空间下，输出的条件概率分布。CART算法分两部分组成：(1)决策树生成：基于训练数据集生成决策树；(2)决策树的剪枝：通过验证数据集对已生成的决策树进行修剪，选出最优的子树，修剪的标准是使得损失函数最小。与CART算法相似的还有ID3、C4.5、C5.0等算法。ID3中根据属性值分割数据，之后该特征不会再起作用，这种快速切割的方式会影响算法的准确率。相比ID3和C4.5算法，CART算法应用要多一些，既可以用于分类也可以用于回归，回归时用平方误差(或均方误差)作为损失函数，以平方误差(或均方误差)最小化为准则[1]。

近年来空气污染严重，因此空气质量问题[2-4]成为了人们关注的焦点。本文根据国家统计局发布的主要污染物(PM2.5、PM10、SO2、NO2、CO、O3)的指标值，采用CART结合广义交叉验证对空气质量指数进行了预测，并与多元线性回归方法进行了比较，结果表明，CART比多元回归线性模型更能有效的预测空气质量指数。

CART被广泛应用在遥感影像分类、区域洪涝灾害损失评估及预测、上市公司财务风险预测等问题研究上[5-9]。但CART在空气质量指数预测学习中的研究较少。目前在对空气质量的相关问题研究中，采用的方法有支持向量机法；计量经济学分析方法；决策树中的C4.5算法等。本文选取对影响空气质量指数的主要六个指标，采用CART对空气质量指数进行的预测建模，通过广义交叉验证选出最佳惩罚参数，从而选出最优的回归树模型。经实例验证表明，CART能较准确的预测出空气质量指数。

1 CART算法原理

1.1 CART的生成

假设X与Y分别为输入和输出变量，且Y为连续变量，给定训练数据集

D={(x1,y1),(x2,y2),…(xN,yN)}

一个回归树对应着输入空间的一个划分以及在划分的单元格上输出的值。这里采用启发式的划分方法，选择第j个变量x(j)和他的取值s，作为切分变量和切分点，并定义两个区域：

α1(j,s)={x|x(j)s} 和 α2(j,s)={x|x(j)>s}

将输入空间划分成L个单元α1,α2,…αL，并且在每个单元αl上有一个固定的输出值βl，因此回归树模型可表示为：

(1.1)

(1.2)

现在的目标是找到最优切分变量j和最优切分点s。具体求解如下：

(1.3)

对固定的出入变量j可以找到最优的切分点s。

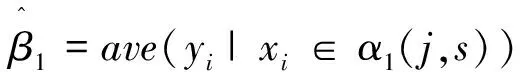
搜索所有输入变量，找到最优的切分点就j，就构成一个对(j,s)，根据这个步骤可以将输入空间划分为两个区域，然后再对每个区域重复上述划分步骤，直到停止。具体的生成算法[10]

[1]如下：

输入：训练数据集D；

输出：回归树f(x)。

在训练数据集所有的输入空间中，递归地将每个区域划分成两个子区域并决定每个子区上的输出值，构建二叉树：

(1)选择最优切分变量j与切分点s，求解

(1.4)

搜索变量j，对固定的切分变量j扫描切分点s，选择是的上式最小值对(j,s)

(2)用选定的对(j,s)划分区域并决定相应的输出值：

α1(j,s)={x|x(j)s} 和 α2(j,s)={x|x(j)>s}

(3)继续对两个子区域选用步骤(1),(2)直到满足停止条件。

(4)将输入空间划分为L个区域α1,α2,…αL，生成决策树：

(1.5)

1.2 CART剪枝

CART算法[10]是从树的底端即叶节点自上而下的剪去一些子树，使决策树变小，可以防止过拟合，使得对未来的数据有更准确的预测。CART算法有两部分组成：首先从决策树T0的底端开始剪枝，直到T0的根节点，形成一个子树序列{T0,T1,…Tn}；然后通过广义交叉验证法在验证数据集上对子树序列进行测试，从中选择最优子树。

在剪枝的过程中，子树的损失函数为：

(1.6)

输入：CART算法生成的决策树T0

输出：最优决策树Tr

(1)设k=0,T=T0。

(1.7)

(4)自上而下的访问内部节点t，假如有g(t)=r，则进行剪枝，并且对叶节点t 以多数表决法决定其类，得到树T。

(5)设k=k+1,rk=r,Tk=T。

(6)如果T不是由根节点单独构成的树，则回到步骤(4)。

(7)采用广义交叉验证法在子树序列{T0,T1,…Tn}中选取最优指数Tr。

2 模型建立

2.1 数据处理

本文数据来源于2012—2014年武汉环境监测站，以SO2、NO2、PM10、CO、O3、PM2.5为自变量，空气质量指数(AQI)为因变量建立决策树回归模型。为了消除量纲的影响，将数据归一化处理，使数据在[0,1]内变动。归一化的公式如下:

xk=(xk-xmin)/(xmax-xmin)

(2.1)

式中，xmin为数据序列中的最小值；xmax为数据序列中的最大值。

对数据进行相关性分析，结果见附表。

附表 相关系数表

为了更够更加直观的分析数据，这里将数据可视化如图1所示：

散 点 图

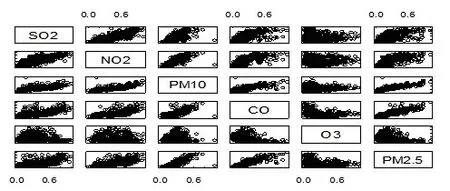
图1 多元散点图

根据图1可知，除了O3与各个变量间的相关性较弱外，其它各个变量间都有比较高的相关性，特别是PM2.5与CO之间相关性很大。

2.2 多元线性回归模型的建立

经对各个变量之间的相关性分析，结果显示，各自变量间相关程度普遍偏高。

多元线性回归进行建模得到回归模型为：

(2.2)

2.3 回归树建立

选定训练数据：先将样本数据随机排序，再把数据集分成训练集和测试集两个互不相交的子集，这里选取75%的数据用作训练集，另外25%的数据作为预测集。由于是分成两个互不相交的子集，故避免了训练子集用在测试集里而导致的误差。因本文采用的是广义交叉验证，故还需对训练集和测试集多次重复上述过程的选取，从而使模型达到最佳的估计。这样选取出来的训练集和测试集重复的几率很小，可以忽略不计。

根据CART算法结合广义交叉验证可得出回归树模型，结果如图2所示：

由图3可以看出数据预测与实际值的预测精度较高。

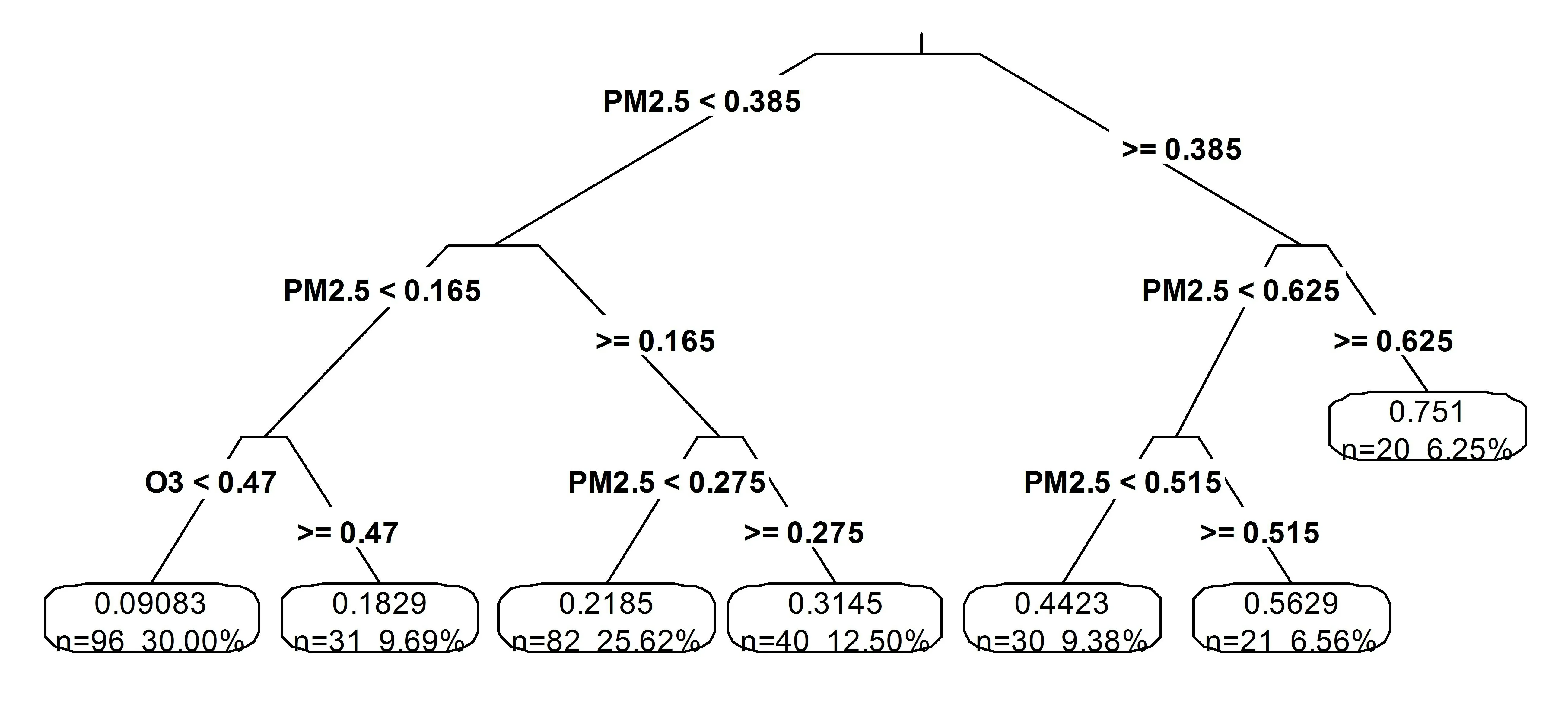
图2 回归树图

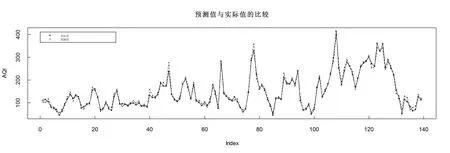
图3 CART算法的预测值与实际值比较曲线图

3 结论

基于CART算法对空气质量预测，采用了广义交叉验证法，选取使得误差达到最小的最优回归树，从而实现了模型的最优化。结果表明，用CART算法对结合广义交叉验证对空气质量指数能有效的预测，而且在最高点和最低点都有较高的预测精度，这体现了CART的在预测时的优势，能给人们带来一定的实用价值。

[1] ROBERT T，JEROME F.统计学习基础——数据挖掘、推理与预测 [M] 范明，等译 .北京：电子工业出版社，2004:40-44.

[2] VARDOULAKIS S，FISHER B，PERICLEOUS K,et al.Modelling air quality in street canyons:a review[J]. Atmospheric Environment，2003，37(2):155-182.

[3] 张丽，李静，葛汝冰.全国主要城市空气质量级别的分类预测——基于支持向量机的视角[J].管理工程师，2013，2(26):57-64.

[4] 李茜，宋金平，张建辉,等.中国城市化对环境空气质量影响的演化规律研究[J].环境科学学报，2013，9(6):15-22.

[5] BREIMAN L，FRIEDMAN J，OLSHEN R，et al. Classification and regression trees[M]. New York:Chapman & Hall, 1949：146-169.

[6] 董连英，邢立新.高光谱图像植被类型的CART决策树分类[J].吉林大学学报，2103,31(1):83-89.

[7] 吉中会，李宁.区域洪涝灾害损失评估及预测的CART模型研究——以湖南省为例[J].地域研究与开发，2012,31(6):106-110.

[8] 王喆,陆楠,周春光.基于决策树归纳的聚类方法与实现[J]. 吉林大学学报(信息科学版)， 2003(2)：39-46.

[9] 陈辉林,夏道勋.基于CART决策树数据挖掘算法的应用研究[J]. 煤炭技术， 2011(10):82-89.

[10] 李航.统计学习方法[M].北京：清华大学出版社，2012:67-73.

Learning of Index of Air Quality Prediction Model Based On CART

CHEN Feng

(College of Mathematics，Physics and Information Engineering， Zhejiang Normal University，Jinhua Zhejiang 321004，China)

In this paper , CART arithmetic and GCV are combined to establish AQI forecasting model. Experimental results show that the regression tree optimized by GCV can forecast AQI effectively. The regression tree has the best forecasting accuracy, compared with Multiple Linear Regression (MLR).

CART; AQI; GCV; MLR

2016-06-23

陈峰(1991-)，男，江西上饶人，硕士研究生，研究方向：机器学习与数据挖掘。E-mail:657306203@qq.com

TP301.6

A

1004-2237(2016)06-0016-06

10.3969/j.issn.1004-2237.2016.06.004