矢量法求解矩形电流激发的磁场空间分布

毛杰键，杨建荣，郭 敏，张腾平，饶欣欣

(1.上饶师范学院物理与电子信息学院，江西 上饶 334001；2. 上饶县尊桥小学，江西 上饶 334115)

矢量法求解矩形电流激发的磁场空间分布

毛杰键1，杨建荣1，郭 敏2，张腾平1，饶欣欣1

(1.上饶师范学院物理与电子信息学院，江西 上饶 334001；2. 上饶县尊桥小学，江西 上饶 334115)

磁感应强度是电磁学中重要的物理矢量，运用矢量运算方法求解磁场，可提高学生解决物理问题的能力和空间想象力，对学生学好物理、用好物理规律具有重要的意义。用矢量运算，求得矩形电流线圈激发的磁场在空间分布的精确解，形象地表明了在导线所在位置处，存在奇点；在线圈平面内，中间的磁场小，靠近线圈导线的磁场大；导线二侧的磁场方向相反；线圈外侧磁场，随距离的增大，很快趋于零；在矩形线圈二导线交点处的磁场大于等距离的它处；在线圈平面附近，z方向的磁场大，x，y方向的磁场小；线圈内的磁场大于线圈外的磁场；磁场方向遵循右手螺旋定则。

矢量；矩形电流；磁场

求解直导线电流在平面内激发的磁场是毕奥-萨法尔定律应用的经典例子，目前的教材中均采用标量积分法，局限于求垂直于平面的磁场[1-2]。本文利用矢量运算法，求解由直导线组成的矩形电流在空间激发的磁场分布。一是提高学生数学应用能力，学会矢量运算方法解决电磁学中的实际问题；二是引导学生推广应用毕奥-萨伐尔定律解决实际工程中复杂的问题；三是由直导线可构成矩形线圈、多边形线圈，而矩形电流线圈作为磁体，在电工电子工程、仪器仪表中具有广泛的应用。本文结果为利用矩形电流线圈解决电工电子工程中的问题，提供精确解。

1 矩形电流线圈在空间任意点激发的磁场的精确解

图1 直角坐标系中的矩形电流线圈

如图1所示,设矩形电流线圈放置在直角坐标系的xoy平面内，z轴垂直矩形线圈平面，并经过矩形对角线交点。设线圈中的电流为I，线圈的长为|AB|=|CD|=2b,与y轴平行；宽为|BC|=|DA|=2a，与x轴平行，空中任意一点为P(x,y,z)。根据毕奥-萨伐尔定律

①

由①式可知，求解B的关键一是矢量运算，二是求积分。

对于AB边，设Q=Q(a,y1,0),则Q点电流源矢量Idl中的dl=0i+dy1j+0k=dy1j , 电流源到场点P的矢量为rp=QP=(x-a)i+(y-y1)j+z k,则

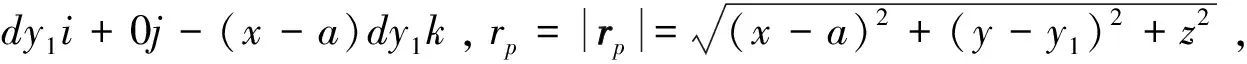
②

式中i,j,k分别为空间直角坐标x,y,z的单位矢量。将②式代入①式，得AB边在P点激发的磁感应强度为：

③

上式积分结果利用了积分关系式

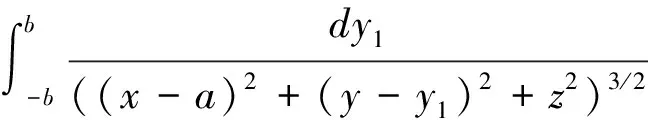
④

同理，对于BC边，设Q=Q(x1,b,0),则矢量

dl=-dx1i+0j+0k=-dx1i, rp=QP=(x-x1)i+(y-b)j+z k，

⑤

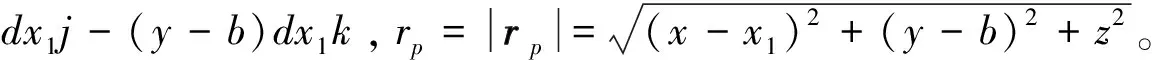
⑥

将⑥式代入①式，并利用④式，可得BC边在P点激发的磁感应强度为

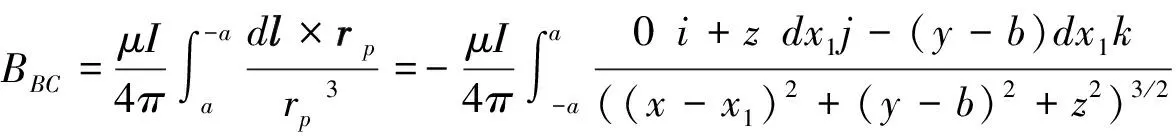
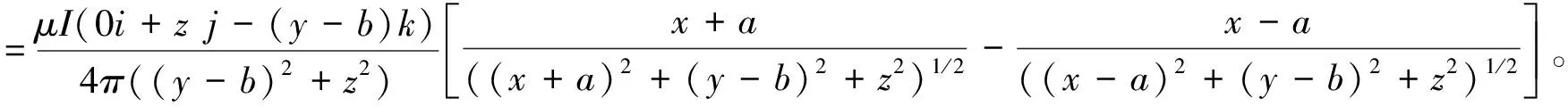
⑦

对于CD边，设Q=Q(-a,y1,0),则矢量

dl=0 i-dy1j+0k=-dy1j , rp=QP=(x+a)i+(y-y1)j+zk ,

⑧

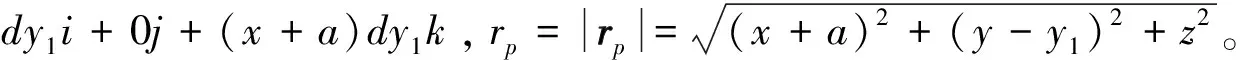
⑨

将⑨式代入①式，并利用④式，可得CD边在P点激发的磁感应强度为

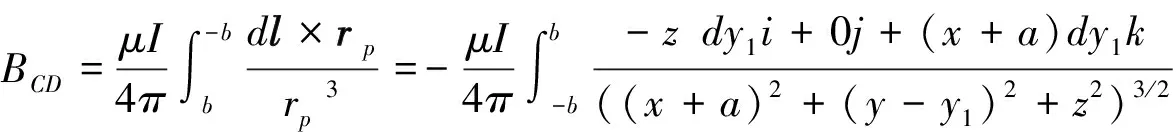
⑩

对于DA边，设Q=Q(x1,-b,0), 则矢量

dl=dx1i+0j+0k=dx1i, rp=QP=(x-x1)i+(y+b)j+zk,

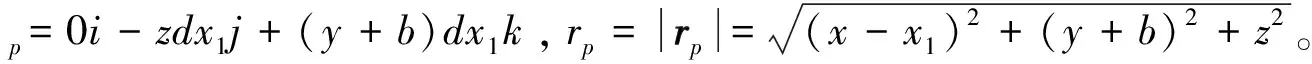
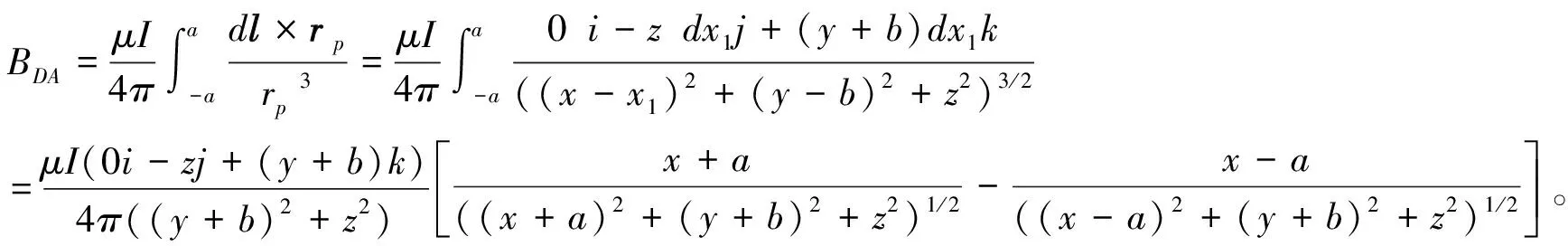
取出j的系数，可得y方向的磁感应强度为

取出k的系数，可得z方向的磁感应强度为

Bp=Bxi+Byj+Bzk 。

2 分析讨论

2.1 一段直导线电流在平面内激发的磁场

考虑AB段电流在yoz平面内激发的磁场。此时AB在yoz平面内，有a=0，x=0，磁场只有垂直于yoz平面的x方向分量，由式可得

结果与教材中利用标量积分法所得结论相同[1-2]。有的文献根据一段直导线的磁场分布式，推导矩形电流在空间的分布，存在复杂的运算[3]，没有上述矢量运算简单明了。

2.2 矩形线圈所在位置z方向的磁场空间分布

μ=1, π=3.14, I=1, a=0.1, b=0.08,

2.2 矩形线圈激发的磁场空间分布

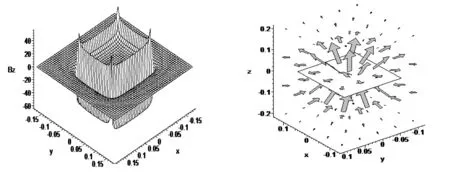
图2 z=0平面，z方向的磁场分布 图3 矩形电流激发的磁场空间分布

3 结论

磁感应强度是电磁学中重要的物理矢量，掌握矢量运算方法，提高矢量运算解决物理问题的能力，对学生学好物理、用好物理规律具有重要的意义。可是在解决物理问题的思维上，学生往往习惯于标量运算，这对后继课程，如电动力学的学习会带来不利的影响。本文介绍了用矢量运算、④式所示的积分关系和毕奥-萨伐尔定律，求得矩形电流线圈激发的磁场在空间分布的精确解。结果表明：在导线所在位置处，存在奇点。在线圈平面内，中间的磁场小，靠近线圈导线的磁场大；导线二侧的磁场方向相反；线圈外侧磁场，随距离的增大，很快趋于零；在矩形线圈二导线交点处的磁场大于等距离的它处；在线圈平面附近，z方向的磁场大，x，y方向的磁场小，远离线圈平面磁场减小，线圈内的磁场大于线圈外的磁场；磁场方向遵循右手螺旋定则。

[1] 赵凯华，陈熙谋.电磁学(第三版)[M].北京:高等教育出版社，2012:245.

[2] 梁灿彬，秦光戎，梁健.电磁学(第二版)[M].北京:高等教育出版社，2010:178.

[3] 邝向军，矩形载流线圈的空间磁场计算[J].四川理工学院学报，2006(2)，19(1):17-20.

Magnetic Field Distribution of Rectangle Coil by Vector Method

MAO Jie-jian1, YANG Jian-rong1, GUO Min2, ZHANG Teng-ping1, RAO Xin-xin1

(1.School of Physics and Electronic Information, Shangrao Normal University, Shangrao Jiangxi 334001, China; 2. Zunqiao Primary School of Shangrao County, Shangrao Jiangxi 334115, China)

Electric field and magnetic field are two important physical vectors in electromagnetics. It has important meanings that students enhance the ability using vector operation to solve physics problems. This paper applies vector method to obtain the exact solution for space distribution of magnetic field excited by rectangle coil. The plots show that there exists singularity in the coil position; in the coil plane, the middle magnetic field is small but big near wire; the magnetic field possesses opposite direction at the two sides of coil ; the outside magnetic field tends quickly to zero with the increasing distance; at the intersection points of two coils, the magnetic field is greater than the other equidistance; near the coil plane, the magnetic field in z direction is big but small along x and y; the magnetic field within the coil is greater than outer; and the magnetic field direction follows the right-hand screw rule.

vector method; rectangle coil; magnetic field

2016-09-01

江西省教育厅科技落地计划项目(KJLD13086)；江西省教改课题(JXJC-13-16-4)；国家级大学生创新创业训练计划项目(201510416003，201510416004)

毛杰键(1962一)，男，江西广丰人，教授，主要从事物理学的教学和研究。E-mail：maojj2006@163.com

O441

A

1004-2237(2016)06-0028-05

10.3969/j.issn.1004-2237.2016.06.006