例谈向量背景下常见动点问题的求解

党忠良 王历权 刘 津

(重庆市育才中学，400050) (重庆市九龙坡区辰光学校，404000)



○解题思路与方法○

例谈向量背景下常见动点问题的求解

党忠良 王历权 刘 津

(重庆市育才中学，400050) (重庆市九龙坡区辰光学校，404000)

一、动点问题在向量中的考察分析

动点的轨迹问题是高考的热点,以向量为背景的动点轨迹和相关最值问题更是高考的宠儿,深受命题者的青睐.这类题目以向量为背景考察向量的线性运算、数量积、面积、动点轨迹方程以及与圆有关的最值问题等相关知识,通过适度联系与综合,在知识交汇处考查学生的数学思维方法和能力．

求解以向量为背景的动点问题需要结合向量的数与形两方面属性,熟练运用数形结合和化归的思想,以明确动点的轨迹为解决问题的基础，因此，更需要有分析动点轨迹的意识．这类题目加大了对考生创新能力、数学思想方法的考查,需要考生根据问题情境,从特殊到一般,从抽象到形象进行不同侧面的分析与探究．

二、常见动点轨迹问题分类例析

1.动点轨迹为直线或线段的向量问题

由三点共线充要条件，易得下述结论：

2.动点轨迹为平面区域的向量问题

评注本题综合了向量基本线性运算、正余弦定理等知识,寻求动点P的运动区域是解题关键.同时，应准确理解并应用三角形内心这一条件,将平行四边形的面积与三角形ABC的面积联系起来．

答案：D.

变式2(2014年陕西高考题) 在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在∆ABC三边围成的区域(含边界)上.

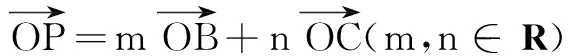
(2)m-n=y-x，最大值为1.

3.动点轨迹为圆的向量问题

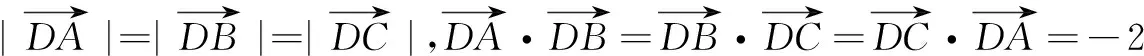
(x-2)2+y2=1.

故选B．

评注本题涵盖向量数量积和圆的相关知识,动点P运动轨迹为圆,需建立坐标系,写出点P运动轨迹方程,通过向量坐标运算，数形结合解决问题．

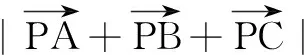
(A)6 (B)7 (C)8 (D)9

答案：B.

变式2(2013年湖南高考题)已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的取值范围是( )

答案：A.

4.隐含动点轨迹的向量问题

例4(2012年安徽高考题)若平面向量a,b满足:|2a-b|≤3，则a·b的最小值是______.

解法1由已知|2a-b|≤3,平方得

4|a|2+|b|2-4a·b≤9.

又4|a|2+|b|2≥4|a||b|

≥-4a·b,

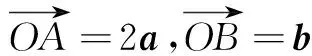
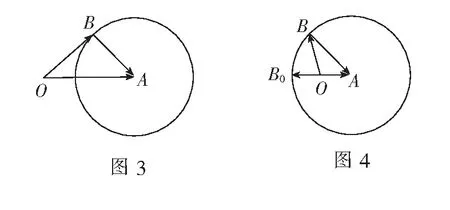
评注本题题干以不等式形式给出,简约但不简单.解法1利用了不等式(i)|a|2+|b|2≥2|a||b|和(ii)-|a||b|≤a·b≤|a||b|,看似简洁但又深感突兀,尤其对使用不等式(ii)左侧进行变形深感困惑．思考之后笔者想到用向量的几何意义来解释,发现该题尤为有趣且意味深长,即得解法2.问题中隐藏着动点的轨迹、均值不等式等“宝藏”，让笔者深感意外的同时又深感必然,想必这就是高考好题和趣题．

答案：选D.

5.构造函数研究动点的向量问题

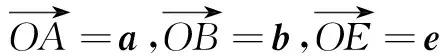
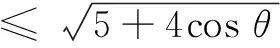
评注本题跟例4解法2一样,先固定一个变量,再寻求此情况下相关量的最值,这种多变量问题中控制变量求边际最值的方法值得注意．本题用函数的观点审视了解法1中放缩的“合理性”,解法2用运动变化的观点建立函数关系是解决变化问题的很好方法.

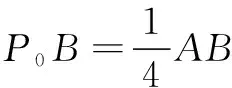
(A)∠ABC=90° (B)∠BAC=90°

(C)AB=AC (D)AC=BC

答案：选D.

故当n=15时,Sn取得最小值,S15=-225.