基于Burgers蠕变模型的圆形隧道内力分析方法对比研究

林文凯，晏启祥，刘羲睿，吴 聪，杨俊哲

(1.西南交通大学交通隧道工程教育部重点实验室，成都 610031;2.神华神东煤炭集团有限责任公司，鄂尔多斯 017200)



基于Burgers蠕变模型的圆形隧道内力分析方法对比研究

林文凯1，晏启祥1，刘羲睿1，吴 聪1，杨俊哲2

(1.西南交通大学交通隧道工程教育部重点实验室，成都 610031;2.神华神东煤炭集团有限责任公司，鄂尔多斯 017200)

以高黎贡山TBM施工的特定段圆形隧道为工程对象，基于围岩蠕变的Burgers模型，提出了隧道衬砌内力计算的地层结构分析法和荷载结构分析法，对比研究两种分析方法的异同点和特点，得出以下结论：(1)地层结构分析法能模拟地层自重应力及其重分布、隧道开挖和支护效应，并能通过蠕变的非线性迭代获得隧道衬砌内力结果，在隧道开挖后围岩蠕变的整个过程中，模拟精度较高，但计算耗时稍长；(2)荷载结构分析法不能考虑地层自重应力以及隧道开挖支护效应，建模相对简单，计算耗时短，但计算前需准备等效节点荷载，对蠕变早期的模拟精度相对较差，对蠕变中后期的模拟结果与地层结构分析法较为一致；(3)综合考虑各种因素，建议围岩蠕变下的隧道衬砌内力分析优先选用地层结构分析法。

隧道；围岩蠕变；衬砌内力；地层结构分析法；荷载结构分析法

岩石的蠕变研究在岩土工程和地下工程领域占有重要的地位。岩石的蠕变研究对于隧道工程的长期稳定性是必不可少的，近年来许多学者研究了岩石蠕变对隧道稳定性的影响[1-2]。王中文等[3]通过对隧道围岩蠕变特性的初衬变形的理论公式，结合规范对隧道二衬支护时间的确定准则，给出了二衬合理支护时机。左清军等[4]通过引入水劣化因子，建立了泥质板岩考虑吸水率的黏弹塑性蠕变本构模型，该模型可用于描述富水泥质板岩隧道围岩的蠕变规律。刘钦等[5]基于软弱破碎岩石试验成果，分析了炭质页岩的蠕变力学特性，研究了隧道软弱破碎围岩的蠕变性质和稳定性。唐葭等[6]基于Burgers蠕变力学模型模拟黏弹性区的蠕变变形，推导考虑围岩蠕变效应的围岩抗力系数公式。吕志涛等[7]研究了考虑岩体蠕变时隧道下穿建筑物施工引起围岩和建筑物的变形规律及特点。与此同时，还有很多学者[8-10]对岩石蠕变特性、岩石蠕变本构模型及蠕变本构模型参数辩识进行了大量研究。

目前，利用组合模型方法模拟岩石蠕变的有Maxwell模型、Kelvin模型、Burgers模型、Bingham模型及西原模型等[11]。本文基于Burgers蠕变模型，分别采用地层结构分析法和荷载结构分析法，研究围岩蠕变对隧道衬砌的力学响应特性，对比2种分析方法的异同和优缺点，为高地应力围岩蠕变条件下隧道衬砌设计内力分析方法的选择提供参考。

1 基于Burgers蠕变模型的圆形隧道内力分析方法

Burgers模型为一个Maxwell和一个Kelvin模型串联所组成的四元件黏弹性模型[12]。该模型适合于大多数具有初始瞬时弹性变形、衰减蠕变及稳定蠕变阶段的岩石，其组成方式如图1所示。

图1 Burgers模型本构示意

Burgers模型的本构方程为

1.1 地层结构分析法

地层结构分析法通常借助有限元软件开展，如ANSYS软件。该软件内置了关于材料非线性黏弹性模型的Prony级数。由于Burgers模型的4个参数不能作为Prony级数输入值，因此需将E1、E2、η1、η2转化为剪切模量的Prony级数参数。

对于Burgers体，ANSYS内置的Prony剪切模量表达式为[13]

式中，g∞为松弛时间无穷大时的相对剪切模量；g1、τ1分别为Maxwell模型的相对剪切模量和松弛时间；g2、τ2分别为Maxwell模型的相对剪切模量和松弛时间。g1=G1/G0，g2=G2/G0，G1、G2分别是Maxwell模型和Maxwell模型的剪切模量，G0为松弛时间为零时的剪切模量。

若将Burgers模型中的弹性模量系数转换为剪切模量则有

式中，n1、n2分别为与黏滞系数和泊松比有关的系数，对于同一种围岩有μ1=μ2。

若以剪切模量表示式(1)，则有

对式(1)进行Laplace变换和Laplace逆变换，可得剪切模量的Prony级数表达式[14-15]

结合式(2)，可发现

G0=G1

g∞=0

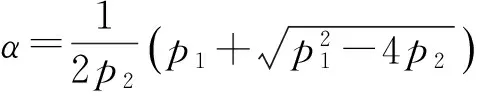
这样就获得了Burgers本构模型在ANSYS中需要输入的4个Prony级数参数g1、g2、τ1、τ2。得到了这些参数，即可利用地层结构分析法计算隧道衬砌的内力。

1.2 荷载结构分析法

对于圆形隧道，假设围岩为黏弹性材料，衬砌为弹性材料，则隧道衬砌荷载的理论分析简图如图2所示。

图2 理论分析简图

首先将地层压力P转化为作用在衬砌上的压力pi，基于Burgers体蠕变模型，可得隧道衬砌上的压力解析解pi为[16]

式中，pi为作用在隧道衬砌上的压力；P为隧道周边地层中原始垂直压力；G、μ、λ分别为围岩的剪切模量、泊松比和侧压力系数；Gc、μc分别为衬砌的剪切模量、泊松比；r0、r1分别为隧道衬砌的外半径和内半径。

对式(6)进行Laplace变换和Laplace逆变换，可得作用荷载的黏弹性解为

这里R1、R2是方程S2+n1S+n0=0两根的相反数。

为求式(7)中的B1、B2、b1、b2，只需在式(8)中令D2=1，m1=M，按式(8)得出的C1、C2、R1、R2即为所求的B1、B2、b1、b2。而式(7)中的C1、C2、R1、R2则按式(8)计算。通过上述公式可得Burger围岩蠕变模型下隧道衬砌周边上的压力。获得了隧道周边压力荷载，即可利用荷载结构分析法计算隧道衬砌的内力。

2 模型建立

为对比围岩蠕变下地层结构分析法和荷载结构分析法两种分析方法的区别，以大瑞铁路高黎贡山隧道某一TBM施工段为分析对象开展研究。取该隧道特定断面进行分析，该段隧道穿过地层为砂岩，前期勘探中测得隧道上方50 m处地层压力为110.44 kPa，侧压力系数为0.34。隧道衬砌为圆形现浇C30混凝土衬砌，内外半径分别为4.0 m和4.5 m。假设隧道掘进开挖后即时支护，分别采用地层结构分析法和荷载结构分析法进行计算。该隧道特定段的围岩和衬砌物理力学参数见表1。

表1 围岩和衬砌力学参数

砂岩的Burgers体蠕变参数以及转化为可输入的Prony级数参数见表2。

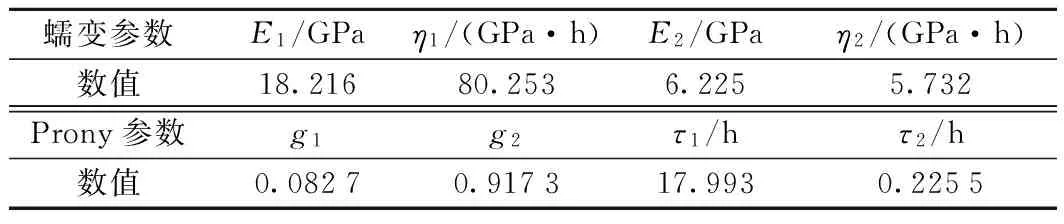
表2 围岩蠕变参数及Prony级数参数

将围岩Burgers蠕变参数转换成的Prony级数参数用于地层结构计算模型分析。地层结构模型边界长度为100 m×100 m，围岩采用具有蠕变功能的PLANE182单元模拟，隧道衬砌采用BEAM3单元模拟，二维地层结构模型见图3。

图3 地层结构模型

根据式(7)并代入相关围岩参数可求得围岩蠕变作用下衬砌周边的压力

pi(t)=74(1+B1e-b1t+B2e-b2t)+

式中，B1=-0.200 1，b1=1.389，B2=-0.706 1，b2=0.016 7，C1=-0.003 2，R1=1.089 5，C2=-0.995 7，R2=2.50×10-4

根据式(9)，作出的隧道衬砌周边上压力见图4。

图4 隧道衬砌周边压力(单位：kPa)

将隧道衬砌上的蠕变压力转化为等效节点力，以便采用荷载结构分析法分析。隧道衬砌采用BEAM3单元模拟，隧道衬砌周边地层约束采用COMBIN14单元，若某个单元受拉，则去掉该4单元，荷载结构分析法模型如图5所示。

图5 荷载结构模型

3 结果对比

隧道开挖蠕变和支护1 d后，地层结构分析法和荷载结构分析法计算的隧道衬砌弯矩图如图6所示。

图6 蠕变和支护1 d后衬砌弯矩图(单位：N·m)

由图6可知，地层结构分析法在隧道开挖1 d后，在拱顶和拱底处隧道衬砌内侧受拉，在左、右拱腰处隧道衬砌内侧受压，衬砌的弯矩最大绝对值为105.869 kN·m。荷载结构分析法在隧道开挖1 d后，在拱顶、拱底、左右拱腰处隧道衬砌内侧受拉，在左、右拱肩和左、右拱脚处隧道衬砌内侧受压，衬砌的弯矩最大绝对值为11.549 kN·m。由于荷载结构分析法中没有考虑隧道开挖导致的围岩二次应力重分布，所以在隧道刚开挖时，荷载结构分析法所获得的隧道衬砌内力值较地层结构分析法要小。

隧道衬砌支护完成360 d后，地层结构分析法和荷载结构分析法获得的隧道衬砌弯矩图如图7所示。

图7 蠕变和支护360 d后衬砌弯矩图(单位：N·m)

由图7可知，两种方法在隧道开挖360 d后隧道衬砌的弯矩图相似，都是在拱顶和拱底处隧道衬砌内侧受拉，在左、右拱腰处隧道衬砌内侧受压。地层结构和荷载结构分析法的弯矩最大绝对值分别为208.081 kN·m和208.363 kN·m。

隧道衬砌支护完成360 d后，地层结构和荷载结构分析法获得的隧道衬砌的内力极值随时间的变化如图8所示。

图8 隧道衬砌内力极值

由图8(a)可知，随着围岩蠕变的时间推移，2种方法计算的弯矩极值有不同程度的增大。对于弯矩最大负值，荷载结构分析法从第1天的-11.5 kN·m增加到第150天的-148.0 kN·m，而地层结构分析法由第1天的-105.9 kN·m增加到第150天的-152.8 kN·m。荷载结构分析法的弯矩最大负值的增大速率大于地层结构分析法。在围岩蠕变第150天到360天期间，两种方法计算的弯矩最大负值基本接近，且增大速率开始减小。弯矩最大正值的变化趋势与弯矩最大负值接近，但在围岩蠕变的第150天至360天期间，荷载结构分析法所得的最大弯矩正值相对于地层结构分析法要小30 kN·m左右。

由图8(b)可知，随着围岩蠕变，隧道衬砌的剪力极值变化规律与弯矩相似。在围岩蠕变的前150天，荷载结构分析法获得的隧道衬砌剪力值增速大于地层结构分析法。围岩蠕变的第150天至360天期间，两种方法计算得出的剪力极值基本接近。隧道衬砌的剪力的最大值和最小值变化趋势也几乎相近。

以下采用地层结构分析法分析围岩蠕变对隧道衬砌位移响应的影响。地层结构分析法隧道衬砌的拱顶、拱底、左拱腰、右拱腰的变形位移随围岩蠕变变化如图9所示。

图9 衬砌典型部位的位移

由图9可以看出：拱顶、拱底、左拱腰、右拱腰都发生朝隧道内部的变形。拱顶的竖向位移在围岩蠕变100天内增速逐渐减小，在第100天后，拱顶竖向位移趋于稳定，变形达-74 mm；拱底的竖直向上位移在围岩蠕变200天内增速逐渐减小，在第200天后，拱底竖向位移趋于稳定，变形达21 mm。左右拱腰的位移变化相对隧道中线对称，在围岩蠕变的第100天趋于稳定，向隧道内部的横向位移为32 mm。

由以上结果可知，在隧道开挖早期，由于荷载结构分析法并没有考虑隧道开挖对围岩二次应力重分布的影响，所以荷载结构分析法计算出的衬砌内力值要相对地层结构分析法要小。随着围岩蠕变时间的增加，2种方法得到的隧道衬砌内力值在围岩蠕变第50天至360天期间逐渐吻合。对比2种方法，地层结构分析法通过对时间的迭代运算可以得到各时刻的内力和变形结果，能模拟隧道开挖支护效应，但耗费计算时间较长，是荷载结构分析法的3倍左右。荷载结构分析法可以方便得到具体时刻的内力结果，耗费计算时间较短，但不能表征随时间围岩非线性蠕变的迭代效果，且计算等效节点荷载相对繁琐。

4 结论

利用地层结构分析法和荷载结构分析法分析了高黎贡山隧道围岩蠕变对隧道衬砌结构内力的影响，得到以下结论。

(1)地层结构分析法不仅能模拟隧道开挖和支护效应，还能考虑地层自重应力及其开挖后的应力重分布，并通过非线性迭代最终获得隧道衬砌各时刻的内力和变形结果，这种分析法与实际工程较为吻合，因此更加合理，不足之处是分析时间稍长，是荷载结构分析法的3倍左右。

(2)荷载结构分析法不能考虑地层自重应力及其应力重分布，只需建立隧道结构模型并在结构上施加蠕变荷载，即可得到具体时刻隧道衬砌的内力，建模相对简单，计算耗时较短，但各时刻等效节点荷载的计算相对繁琐，需在计算机分析前提前做好等效节点荷载的计算。

(3)在围岩蠕变早期，荷载结构分析法分析的内力结果相较地层结构分析法要小；然而，在围岩蠕变的中后期，荷载结构分析法获得的内力结果逐渐接近地层结构分析法，表明随着围岩蠕变时间的变长，蠕变荷载开始明显大于地层自重荷载并居主导地位，此时，采用荷载结构分析法也具有较好的精度。

综合考虑各种因素，建议围岩蠕变下的隧道衬砌内力分析优先采用地层结构分析法，特别是隧道开挖后较短时间内初期支护等的内力计算，采用地层结构分析法相较荷载结构分析法有更好的精度。

[1] 康永刚，张秀娥.一种改进的岩石蠕变本构模型[J].岩土力学，2014，35(4):1049-1055.

[2] 汪为巍，王文星.金川高应力软岩蠕变特性及破坏形态试验研究[J].岩石力学与工程学报，2014，33(S1):2794-2801.

[3] 王中文，方建勤，夏才初，等.考虑围岩蠕变特性的隧道二衬合理支护时机确定方法[J].岩石力学与工程学报，2010，29(S1):3241-3246.

[4] 左清军，吴立，李波.富水泥质板岩隧道围岩蠕变力学特性研究[J].岩石力学与工程学报，2015，34(10): 2047-2056.

[5] 刘钦，李术才，李利平，等.软弱破碎围岩隧道炭质页岩蠕变特性试验研究[J].岩土力学，2012，33(增2):21-28.

[6] 唐葭，邓宗伟，蒋建清.考虑蠕变影响的隧道围岩抗力系数计算方法[J].中南大学学报(自然科学版)，2014，45(4):1281-1287.

[7] 吕志涛，张生，邓怡虎，等.围岩蠕变对隧道下穿建筑物施工变形的影响[J].地下空间与工程学报，2014，10(6):1380-1386.

[8] 李亚丽，于怀昌，刘汉东.三轴压缩下粉砂质泥岩蠕变本构模型研究[J].岩石力学，2012，33(7):2035-2040.

[9] 田洪铭，陈卫忠，田田，等.软岩蠕变损伤特性的试验与理论研究[J].岩石力学与工程学报，2012，31(3):610-617.

[10]胡波，王宗林，梁冰，等.岩石蠕变特性试验研究[J].实验力学，2015，30(4):438-446.

[11]康永刚，张秀娥.岩石蠕变的非定常分数伯格斯模型[J].岩土力学，2011，32(11):3237-3241.

[12]熊良宵，杨林德，张尧.岩石的非定常Burgers模型[J].中南大学学报(自然科学版)，2010，41(2):679-684.

[13]姚超凡.盾构法深长煤矿斜井围岩蠕变对衬砌结构受力影响分析[D].成都:西南交通大学，2015.

[14]左清军，吴立，李波，等.富水泥质板岩隧道围岩蠕变力学特性研究[J]. 岩石力学与工程学报，2015，34(10):2047-2056.

[15]王丰胜.基于Burgers黏弹性模型的沥青路面蠕变变形规律三维有限元分析[J].工业建筑，2014，44(3):104-109.

[16]周培德，朱本珍，毛坚强.流变力学原理及其在岩土工程中的应用[M].成都:西南交通大学出版社，1995.

Comparative Study on Internal Force Analysis Methods of Circular Tunnel based on Burgers Creep Model

LIN Wen-kai1， YAN Qi-xiang1， LIU Xi-rui1， WU Cong1， YANG Jun-zhe2

(1.Key Laboratory of Transportation Tunnel Engineering Ministry of Education， Southwest Jiaotong University，Chengdu 610031， China; 2.Shenhua Shendong Coal Group Corporation Limited， Ordos 017200， China)

In view of the circular tunnel of Gaoligong Mountain constructed with TBM， stratum structure analysis method and load structure analysis method are conducted to calculate the internal force of tunnel lining based on the Burgers model of rock creep. Based on the similarities and differences of the two methods， conclusions are as follows: (1) the stratum structure analysis method can simulate geostatic stress of the formation and its redistribution， effect of tunnel excavation and support， the internal force of tunnel lining can be obtained by nonlinear iteration of creep， the simulation accuracy is higher in the whole process of rock creep after tunnel excavation， but the calculation time is slightly longer; (2) the load structure analysis method fails to take into account of the geostatic stress of the formation and the effect of tunnel excavation and support， the modeling is relatively simple and the computation time is short， but the equivalent nodal load needs to be prepared before calculation， the simulation precision is relatively low in the early stage of creep， and the simulation results in the mid-late stages of creep are consistent with that of the stratum structure analysis method; (3) based on various factors， the stratum structure analysis method is prioritized for the analysis of internal force of tunnel lining subject to rock creep．

Tunnel; Rock creep; Lining internal force; Stratum structure analysis method; Load structure analysis method

2016-05-05；

2016-05-13

国家科技支撑计划(2013BAB10B04)；中国铁路总公司科技研发课题(2014G004-H)

林文凯(1991—)，男，硕士研究生，主要从事隧道与地下工程等方面的研究，E-mail：1025130724@qq.com。

1004-2954(2016)12-0104-05

U451

A

10.13238/j.issn.1004-2954.2016.12.023