铸造用大颗粒型砂气力输送行为的数值模拟研究
2016-12-30
(兰州理工大学,甘肃兰州 730050)
铸造用大颗粒型砂气力输送行为的数值模拟研究
贾少伟,袁子洲
(兰州理工大学,甘肃兰州 730050)
对铸造用型砂颗粒在垂直提升管中的气力输送过程往往需要靠经验公式来设计计算。通过采用数值模拟的方法,基于FLUENT模拟过程中对气相采用k-ε标准方程模型,将型砂固体颗粒看作拟流体,建立了气力输送的数学物理模型和计算方法,对粒径大、真密度高铸造用型砂颗粒在垂直提升管中的流动特性进行了模拟分析。模拟结果表明,当空气输送速度保持不变时,气固两相在垂直提升管中存在加速段及恒速段;在不同的空气输送速度下,气固两相在垂直提升管中都存在加速段及恒速段,而且随着空气输送速度的增加,固相颗粒在提升管内的停留时间越短,即固相颗粒的输送速度越高。
型砂;气力输送;拟流体;数值模拟
消失模铸造技术是一种近无余量、精确成形的新型铸造技术,被称为是“代表21世纪的铸造新技术”[1]。
目前,传统消失模铸造生产中,对型砂往往采用机械输送的方式。这种输送方式设备占地面积大,生产效率低,环境污染大,严重制约了以经济绿色为主题的生产方式的发展。气力输送因设备简单、占地面积小,环境污染小等优点[2],在铸造生产中得到了应用。
长期以来,针对气力输送过程国内外学者进行了广泛而持久的研究。例如,Huber等人[3]对输送管中的稀相气固两相流进行了三维数值模拟,预测了不同管道内横截面的固相浓度分布状况;Grzegorzt等人[4]研究了垂直提升管中加速区的流动特性,结合阻力公式和单流体模型,预测了球形以及非球形颗粒在垂直提升管中加速区的压降特性;郭印诚等人[5]运用k-ε-kp模型模拟了提升管中的气固两相流,得到了与冷态实验基本相符的结果。
综上所述,气力输送过程的研究大都集中在浓度低、粒径小的物料输送过程的研究上,对粒径大、真密度高的型砂的气力输送的研究相对还较少[6]。本文针对粒径大、真密度高铸造用型砂颗粒的气力输送问题,采用数值模拟的方法,对垂直提升管中20目石英砂的输送过程进行了模拟分析,为气力输送在大颗粒、高真密度物料输送中的应用奠定基础。
1 数学模型
以颗粒动力学为理论基础的欧拉双流体流动模型,其定常状态下浓相气力输送的数学模型如下:
气相连续方程:

固相颗粒连续方程:

气相动量方程:

固相颗粒动量方程:

其中,φg表示气相的体积分数,φs表示固相的体积分数,φg+φs=1;ugi、ugj、usi、usj分别为气相和固相的瞬时在i、j方向的分量;gj表示当地重力加速度j方向的分量;p表示压力;Fsgi表示固相对气相的作用力;Fgsi表示气相对固相的作用力;τsij表示固相剪切应力;τgij表示气相的剪切应力;ρg表示气相密度;ρs表示固相密度。
在固相拟流体模型即欧拉双流体模型[7-9]中,选取了求解固相颗粒的体积、动力及摩擦粘性系数的模型。其种体积粘度选用Lun-et-al模型,动力粘性选用Gidaspow模型,摩擦粘度选用Schaeffer模型。
利用FLUENT软件的前处理器GAMBIT对消失模型砂气力输送的垂直提升管建立相应的几何模型[10、11],并对所建立的几何模型进行网格划分,垂直提升管网格划分示意图如图1所示。

图1 垂直提升管网格划分示意图
2 边界条件
2.1 气相边界
1)入口边界:假设气相在入口截面的径向速度为零,管道中轴向速度服从湍流流动充分发展的状况,湍流动能k取值为气相流动平均动能的1%,则湍流动能耗散取ε=0.1k2。
2)出口边界:达到稳定流动状态时候的管流条件,即:

3)壁面:壁面条件取NO SLIP(无滑移),即r=R时,ug=vg=k=ε。
4)管道中心:中心取对称,即ρs,υg=0,
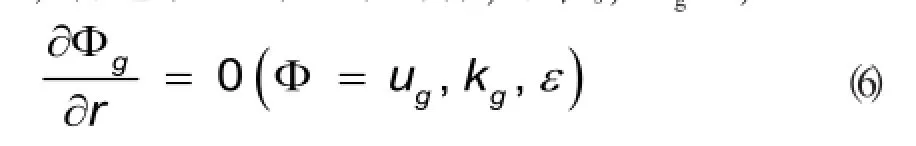
2.2 固相边界:
1)入口边界:均匀入口,轴向速度us=Gs/(αsρs)。其中,αs为给定的值;Gs为被输送物料颗粒的质量流量。径向速度为零,湍流动能k取值为固相流动平均动能的0.8%。
2)出口边界:达到稳定流动状态时候的管流条件,即:

3)壁面:固相颗粒在输送管道壁面附近边界层流动时,径向速度为0,与管道壁面平行的轴向速度us和固相颗粒的湍流动能的边界需从全局考虑。
4)管道中心:中心对称,即r=0,υs=0

3 计算结果与分析
在FLUENT中进行模拟计算时,标准大气压下,室温空气,气固两相物性参数见表1。

表1 气相与固相颗粒的物性参数
3.1 空气速度为15 m/s,石英砂颗粒在垂直提升管中的运动状况
1)提升管不同高度处气固两相的速度分布
首先对输送空气速度为15 m/s时提升管内的气力输送过程进行计算。图2为固相颗粒垂直提升管中不同截面处的速度分布曲线图,图3为气相颗粒垂直提升管中不同截面处的速度分布曲线图。从图2和图3中可以看出垂直提升过程当中,从固相颗粒与气相汇合到两相达到稳定输送的状态,大致可以分为加速段和恒速段两个阶段。从图2和图3中也可以看出,距离管底1 m处到2 m处属于加速段,从2 m处到10 m处属于恒速段。固相颗粒从入口处到加速段,初始阶段固相颗粒的速度比较低,但是在高速气体的曳力作用下开始加速,起始加速很快,随着管长不断的增加,气体对固相颗粒的曳力作用逐渐减小,两相滑移速度随之减小,颗粒加速度减小、速度增加减缓。随着颗粒的继续加速,颗粒重力和颗粒与管道之间的摩擦力与气体作用在颗粒上的曳力达到平衡状态。之后气固两相以恒定的速度继续向上运动,即达到恒速段[12]。
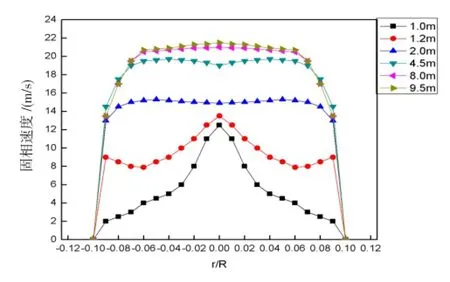
图2 不同高度截面处固相颗粒速度分布

图3 不同高度截面处气相速度分布
2)输送管道沿程的压力和速度分布
管道内的压降也是气力输送过程中比较重要的一个参数[13],图4为轴向平均静压曲线图。从图4中可以获得以下信息,输送管道内沿程的压力在逐渐减小,而且压力梯度在固相颗粒入口处开始减小,而在固相颗粒与气相汇合处压力梯度逐渐增大。

图4 垂直提升管中轴向平均静压曲线图
3.2 不同风速下,提升管中石英砂颗粒的运动状况
图 5为空气输送速度为 10、12及 15 m/s 时,垂直提升管不同高度处的固相颗粒速度分布图。

(a)1.2 m截面处的速度分布

(b)2 m截面处的速度分布

(c)4.5 m截面处的速度分布

图5 不同空气输送速度下不同高度截面处的速度分布
在垂直提升管道内,不同的输送速度下,在管道的1.2~2 m处,固相颗粒靠近壁面加速较慢而靠近中心附近加速较快;在4.5~8 m处,中心速度虽略大于壁面速度,但由于相差不大,已逐渐趋于平稳,而在这段管道内固相颗粒的轴向速度基本无变化。从而也表明之前所提到的加速段与恒速段的说法。最后在输送量保持不变的情况下,在管道的相同高度处,空气输送速度增大之后,固相颗粒的向上速度也会增大。
4 结论
当空气输送速度保持不变时,气固两相在垂直提升管中存在加速段及恒速段,输送管道内沿程压力愈来愈小,压力梯度在固相颗粒入口处开始减小,在固相颗粒与气相汇合处增大;当空气输送速度变动时,气固两相在垂直提升管中仍存在加速段及恒速段,但随着空气输送速度的增加,固相颗粒在提升管内的停留时间越短,也即固相颗粒的输送速度越高。
[1] 樊自田,蒋文明. 消失模铸造技术现状及发展趋势[J]. 铸造,2012,06:583-591.
[2] 米云. 挥发窑烟尘气力输送系统的设计[J]. 稀有金属与硬质合金,2009,02:28-30.
[3] HUBER N, SOMMERFELD M. Modeling and numerical calculation of dilute-phase pneumatic conveying in pipe systems[J]. Power Technology,1998,99:90-101.
[4] Grzegorzt,Investigationof the acceleration conveying[J],Power technology,2002,99:106-127.
[5] 郭印诚,王希麟,林文漪等. 提升管反应器内气粒两相流动的数值模拟,第七届计算传热学会议论文集[C],北京,1997.217-224.
[6] 谢灼利. 密相悬浮气力输送过程及其数值模拟研究[D].北京化工大学,2001.
[7] 周力行. 湍流气粒两相流动和燃烧的理论与数值模拟[M].北京:科学出版社,1994.
[8] 岑可法,樊建人. 工程气固多相流动的理论及计算[M].杭州:浙江大学出版社,1990.
[9] 岑可法,樊建人. 燃烧流体力学[M].北京:水利电力出版社,1991.
[10] 王福军. 计算流体动力学分析—CFD软件原理与运用[M].北京.清华大学出版社:2004.9.
[11] 于勇. FLUENT入门与进阶教程[M].北京.北京理工大学出版社:2008.9.
[12] Benyahia S. Analys is of s olid flow patterns and mixing in gas/solid flow systems[J]: Illinois Institute of technology, Chicago.USA:1999.
[13] 林江. 气力输送系统中加速区气固两相流动特性的研究[J],浙江大学学报,2004,38(7).
Numerical simulation of pneumatic conveying behavior based on large granule molding sand in casting
JIA ShaoWei, YUAN ZiZhou
( Lanzhou University of Technology, Lanzhou 730050, Gansu,China)
Pneumatic conveying process of molding sand particles in vertical riser pipe often need to rely on experience design and calculation formula to this issue. Simulation analysis of flow characteristics in vertical riser pipe was carried aiming at the large particle size, high density of molding sand granule through numerical simulation method. Based on FLUENT simulation for gas phase in the process of the k-epsilon standard equation model, molding sand was taken as continuum or Quasi-fluid, and mathematical model and calculation method for pneumatic conveying was built up. The simulation results reveal that, gas-solid two phase exist accelerating and constant speed in the vertical riser pipe when the air speed stays constant; Gas-solid two phase exist accelerating and constant speed in the vertical riser pipe even when the air convey in different speeds. And with the increase of the air conveyor speed, the residence time of solid particles in vertical riser pipe reduce, the solids conveyor speed increase.
molding sand; pneumatic conveying; quasi–fluid; numerical simulation
TG231.1;
A;
1 006-9658(2016)04-0018-04
10.3969/j.issn.1 006-9 658.2016.04.004
2016-01-11
稿件编号:1601-1204
贾少伟(1990—),男,硕士,主要研究方向消失模铸造工艺及设备研究.
