平面向量的教材分析与解题策略研究

河北省石家庄市第十七中学(050056) 赵然

平面向量的教材分析与解题策略研究

河北省石家庄市第十七中学(050056) 赵然

一、向量的地位与作用

向量在数学和物理学中应用很广,在解析几何中应用更为直接,用向量方法特别便于研究空间里涉及直线和平面的各种问题.从数学发展史来看,在历史上很长一段时间,空间的向量结构并未被数学家认识.直到19世界末20世纪初,人们才把空间的性质与向量运算联系起来,使向量成为一套优良运算通性的数学体系.

向量是近代数学中重要和基本的数学概念之一,有深刻的几何背景,是解决几何问题的有力工具.向量概念引入后,全等和平行(平移)、相似、垂直、勾股定理就可转化为向量的加(减)法、数乘向量、数量积运算,从而把图形的基本性质转化为向量的运算体系.向量是沟通代数、几何与三角函数的一种工具,有着极其丰富的实际背景.

在高中数学中引入向量,是适应时代发展对数学教学的需要,也是为学生提供一种重要的、有价值的数学工具,同时又创设了能促使学生从一种新角度来进行数学思维的情景,从而能更完整、更合理的构建学生基础知识与基本技能.

二、《平面向量》章节的教材内容分析与思想方法

向量作为沟通数和形的重要工具,是现代数学的基本概念之一.在本章介绍向量概念时,重点说明了向量与数量的区别,然后又重新规定了向量代数的部分运算法则,包括加法、减法、实数与向量的积、向量的数量积的运算法则.之后,又将向量与坐标联系起来.

平面向量有着清晰的三条主线:符号形式、几何形式、坐标形式.符号形式与坐标形式反映了向量的数字抽象化:几何形式反映了向量的图形直观化,两者相辅相成、相得益彰.所以数形结合思想是解决向量问题的最常用的数学思想.平面向量的这种特点简洁直观的表示如下.

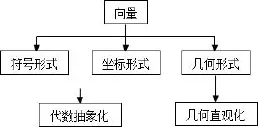
图1

高中数学平面向量的知识体系主要包括向量的定义、向量的运算、向量的位置关系,而每一块的每一点知识都对应着向量的三种表现形式:符号、图形、坐标.所以把《平面向量》章节看似凌乱的知识,可以通过以下表格系统的呈现出来.

几何图形代数符号坐标向量的定义向量表示有向线段→a,→b,-→AB→a=(x1,y1),→b=(x2,y2) |→a|=√向量大小|→a|2=→a2有向线段的长度x21+y21零向量→0长度为0,方向任意→0=(0,0)单位向量→a|→a|长度为1,方向不定(x,y),x2+y2=1→a=→b相等向量长度相等,方向相同x1=x2,y1=y2相反向量长度相等,方向相反x1=-x2,y1=-y2BC=-→AC-→→a=-→b向量的运算平行四边形、三角形加法AB+--→→a+→b=(x1+x2,y1+y2)减法→AB-→AC=→CB三角形法则→a-→b=(x1-x2,y1-y2)数乘长度|λ→a|=|λ||→a|方向由λ的正负决定λ→a=(λx1,λy1)λ→a数量积→a·→b=|→a||→b|cos〈→a,→b〉一个向量的长度乘以另一个向量在其方向上的投影→a·→b=x1x2+y1y2向量的位置关系平行→a=λ→b〈→a,→b〉=0°或180°x1=λx2,y1=λy2垂直→a·→b=0〈→a,→b〉=90°x1x2+y1y2=0夹角cos〈→a,→b〉=→a·→b|→a||→b| cos〈→a,→b〉= x1x2+y1y2√x21+y21·√x22+y22

本章的思想方法有:数形结合思想、转化思想、方程思想、函数思想、建模思想.数形结合思想体现于向量的几何形式和代数形式,几何运算和代数运算的紧密联系,也体现于解决问题中的以形助数,以数解形,数形共存.

图2

转化思想体现在几何结构与代数结构的相互转化:在向量的模计算,起点不在原点的向量转化为起点在原点的向量,从而得到两点的距离:向量模的运算转化为向量的运算:向量的定比分点坐标关系可以转化为向量共线关系:函数图象按向量平移转化为函数图象按上下左右平移:解斜三角形问题中边角条件相互转化.

例2. 平面向量则这样的向量有( )

A.1个 B.2个 C.3个 D.4个

方程思想体现在用向量解决几何图形中线段的比例关系,求满足条件的点的坐标,解斜三角形问题中计算边或角.

例3. 平面内给定三个向量求满足→a=m→b+n→c的实数.

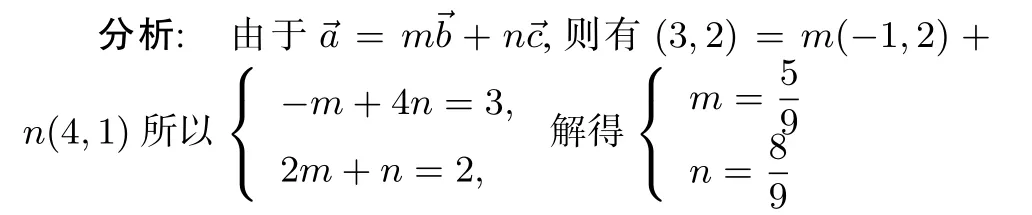
本题将向量表达式转化为代数表达式,考查方程思想的应用.

函数思想体现在向量与三角函数的关系中,同时也较多的体现在一些看似独立的向量问题中.

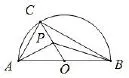
图3

三、平面向量问题的解题策略分析

无论试题如何变化,代数符号、图形、坐标是平面向量的三种体现形式这是永远不会改变的,换句话说任何一道关于向量的试题都可以从向量的代数运算、图形运算、坐标运算三条思路来探寻解决问题的突破口.下面我通过几个典型例题加以说明.

例5. 2008年浙江理科第9题已知是平面内两个互相垂直的单位向量,若向量则 |→c|的最大值是( )

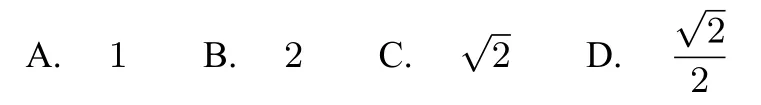
本小题主要考查向量的数量积及向量模的相关运算问题,属于中档难度试题,题目新颖、解法多样.答案为C

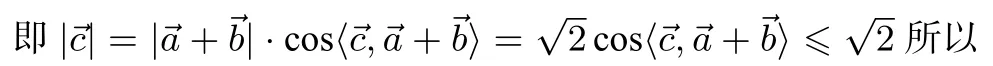
图4

思路二:利用向量的几何运算,通过向量的图像特征构造已知条件,挖掘、延伸已知条件.由于与垂直,所以A,B,C,D四点共圆.以点A为起点的向量→c的终点在以BD为直径的圆上.

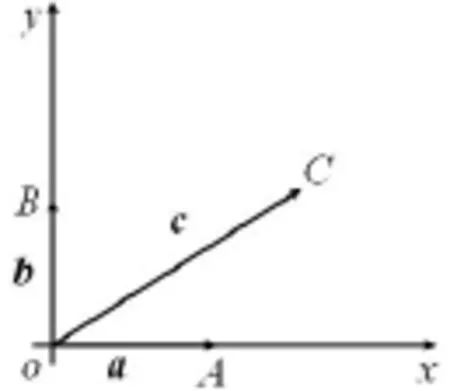
图5

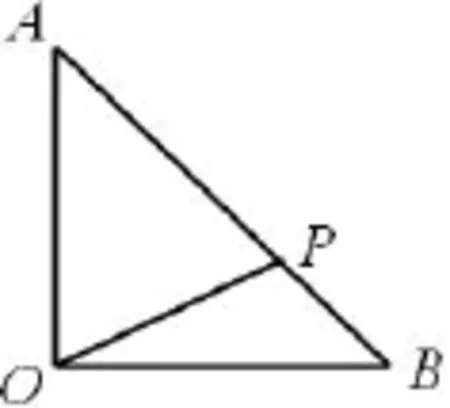
图6

这道题难度较大,特别是如果单纯的通过向量的几何形式构建已知条件,难以实现:但是发现∠AOB为直角,所以考虑建立坐标系,利用向量的坐标运算处理条件.

所以产生了第一种思路:

图7

第二种思路:

综上所述,在教学中应该以向量的三种表示为纲,建构知识网络.以三种表示下的三种运算理清知识结构.然后沟通与函数,三角、几何的关系.向量的三种解题策略展现了解决向量问题的三种解题思路,在教学中应注重一法多题与一题多法的应用,通过一法多题揭示方法的本质特点:通过一题多法建立方法间的联系,拓宽解题思路.从而建立向量的知识方法体系,提高解决向量问题综合能力.