从一道习题探究椭圆、双曲线新的统一

广东省佛山市第一中学(528300) 杨哲

从一道习题探究椭圆、双曲线新的统一

广东省佛山市第一中学(528300) 杨哲

《数学教学通讯》(中等教育)2013年4期、12期分别发表郭新祝老师、周金兰的论文《在极坐标系中椭圆、双曲线、抛物线方程的统一》、《也谈在极坐标系中椭圆、双曲线、抛物线方程的统一》,探究教材(苏教版选修4-4)中《圆锥曲线的极坐标方程》知识点,给出了在椭圆的左、右、上、下焦点情况下的圆锥曲线极坐标方程.受此启发,笔者从另外角度进一步探究.

例题:(人教版高中数学课本选修2-1第50页,B组第2题)一动圆与圆F:x2+y2+6x+5=0外切,同时与圆F′:x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么曲线.

解: 先回顾文中需要用到的以下定义:

椭圆第一定义:到两定点距离之和为定值的点的轨迹是椭圆.

双曲线第一定义:到两定点距离之差的绝对值为定值的点的轨迹是双曲线.

设动圆圆心为P,半径为R:动圆与圆F的圆心距为d1,动圆与圆F′的圆心距为d2,由已知条件,将两定圆方程标准化得:

(x+3)2+y2=4:(x-3)2+y2=100,从而知道定圆圆心坐标分别为F(-3,0)与F′(3,0):圆F的半径R1=2,圆F′的半径R2=10:所以,由动圆P与圆F外切,有d1=R+R1=R+2:由动圆P与圆F′内切,有d2=R2-R=10-R.故d1+d2=12,为定值,由椭圆的第一定义及椭圆的标准方程,知a=6,c=3从而b2=a2-c2=27,故轨迹是椭圆,图1是用几何画板画出的示意图,动圆圆心P的轨迹是一椭圆.

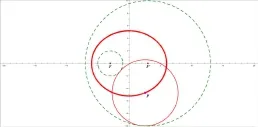
图1 动圆圆心P的轨迹

这类习题通常给定了两个定圆的方程,以及动圆和定圆相切的方法,再来求动圆圆心的轨迹,最后结果通常是椭圆,或是双曲线的一支.那么,如果把特殊性的条件去掉,只关注动圆和定圆相切,是否会为寻找椭圆、双曲线新的统一提供可能?根据以上猜想,提出以下问题:

若动圆P分别与定圆F、F′相切,求点P的轨迹C.

(一)问题分析

设动圆的半径为R,定圆F的半径为R1,定圆F′的半径为R2,且R1＞R2.(下文称圆F为“大圆”,圆F′为“小圆”,假设大圆在小圆左边)分别用d1与d2表示动圆圆心P与F、F′的距离.

由于问题未给出足够的限制条件,必须分类讨论,不难发现,问题的变量有两个,分别是:

①动圆P与两个定圆怎么相切?

②两个定圆的位置关系是什么?

此外,由于我们是在圆锥曲线的范畴内讨论这个问题,故点P的轨迹不是圆锥曲线的情况应当舍去.且以两定圆圆心中点为坐标原点,两圆心所在直线为X轴,建立坐标系.

(二)问题的分类讨论

动圆P与两个定圆相切的情况有内切与外切两种,而内切又分动圆在外、大(小)圆在外两类.考虑到这第一个变量类别较少,故先考虑问题的第一个变量.以动圆与定圆如何相切作为分类标准,列出所有可能的情况:

(1)d1=R+R1,d2=R+R2,与两圆均外切

(2)d1=R-R1,d2=R-R2,与两圆均内切且动圆在外

(3)d1=R+R1,d2=R-R2,与大圆外切,与小圆内切且动圆在外

(4)d1=R+R1,d2=R2-R,,与大圆外切,与小圆内切且小圆在外

(5)d1=R-R1,d2=R+R2,与大圆内切且动圆在外,与小圆外切

(6)d1=R-R1,d2=R2-R,与大圆内切且动圆在外,与小圆内切且小圆在外

(7)d1=R1-R,d2=R+R2,与大圆内切且大圆在外,与小圆外切

(8)d1=R1-R,d2=R-R2,与大圆内切且大圆在外,与小圆内切且动圆在外

(9)d1=R1-R,d2=R2+R,与大圆内切且大圆在外,与小圆内切且小圆在外

从代数角度看,第(6)种情况由于(d1+d2)=(R2-R1)＜0,故动圆圆心轨迹不存在.(事实上,也无法通过作图作出第(6)种情况)

此时根据椭圆和双曲线的第一定义,我们可以知道在上述九种情况里,若d1+d2为大于零的定值,则P点轨迹是椭圆:若d1-d2或d2-d1为大于零的定值,则P点轨迹是双曲线(的一支).

再考虑问题的第二个变量:两个定圆位置关系.两个定圆位置关系有外离、外切、相交、内切、内含五种.

两个定圆的位置关系可以通过线段FF′的长度与(R1+R2)确定.另一方面,通过例题的解答我们意识到,在此类问题中,椭圆或双曲线(标准方程中)的a与c值可通过2a=(d1±d2):2c=(FF′)确定.然而,椭圆与双曲线方程的a与c值大小有规定,在椭圆中a＞c,在双曲线中a＜c.而同时2a=(d1±d2)又与R1、R2有关,(例如(1)中d1-d2=R1-R2)从而通过a与c的大小关系确定两圆的位置关系.

对于动圆圆心轨迹为椭圆的情况:(即d1+d2为大于零的定值)

先看情况(4):第一步,先有2a=(d1+d2)=(R1+R2):而在这个椭圆中,(FF′)=2c＜2a=R1+R2,即两定圆圆心距小于半径之和,故此时两定圆相交、内切或内含.第二步,再结合情况(4)的文字描述:“与大圆外切,与小圆内切且小圆在外”,通过画图可知,两个定圆不可能内切、内含.故对于情况(4),两定圆只能相交.通过类似的“两步走”,我们可以得出:

情况(7),两定圆可以相交、内切、内含(2a=d1+d2=R1+R2)

情况(8),两定圆只能内含(2a=d1+d2=R1-R2)

对于动圆圆心轨迹为双曲线的情况:(即d1-d2或d2-d1为大于零的定值)

情况(1),两定圆可以外离、外切、相交(2a=d1-d2=R1-R2) (双曲线右支)

情况(2),两定圆可以外离、外切、相交(2a=d2-d1=R1-R2) (双曲线左支)

情况(3),两定圆只能外离(2a=d1-d2=R1+R2) (双曲线右支)

情况(5),两定圆只能外离(2a=d2-d1=R1+R2) (双曲线左支)

情况(9),两定圆只能相交(2a=d1-d2=R1-R2) (双曲线右支)

事实上,动圆与两定圆相切,若动圆圆心轨迹是双曲线,那么双曲线必然只能是一支,这是因为d1与d2相减时,被减数与减数是固定的,没有像双曲线第一定义中加上距离差的绝对值.但是在上面的讨论中,我们发现在不同的情况里,有时两个定圆的位置关系是可以相同的,如第(1)与第(2)种:第(3)与第(5)种,恰巧这两对情况的a值相等,左右支对应.这暗示在这个问题中,用求动圆圆心轨迹的方法也可以描出完整的双曲线,只需将两种情况合并即可.我们先放下这个发现,来看看还有什么有趣的现象发生.我们惊讶地发现,对于定义出双曲线的第(9)种与第(1)种情况均可在两定圆相交时成立,并且a值相等,但是它们却都是双曲线的右支,这是为什么呢?难道不同种情况会有重复吗?不妨作出图2一目了然.

图2 动圆与定圆相切示意1

图2 是利用几何画板作出的,F、F′是两定圆的圆心,且这两个定圆相交,圆P是动圆(包含第(1)、(9)种情况的动圆).蓝色的圆系是第(1)种情况,红色的圆系是第(9)种情况.青色线代表第(1)种情况的P点轨迹,红色线则代表第(9)种情况的P点轨迹.

我们注意到,两定圆相交时,第(1)和(9)种情况共同构成了一条完整的双曲线右支.实际上,两定圆相交时,这种轨迹互补的情况也会出现在椭圆中.把轨迹互补的情况同时在一个图中展现,即为图3.

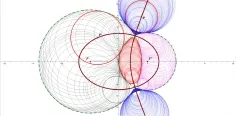
图3 动圆与定圆相切示意2

(说明:判断轨迹是否互补只需看两定圆相交时不同情况的a值是否相等.之所以选择两定圆相交,是因为两定圆相交时P点的轨迹种类全)

图3中,F、F′是两定圆的圆心,且这两个定圆相交.圆P是包含第(1)、(9)种情况的动圆:圆P′是包含第(4)、(7)种情况的动圆.图中黑色的圆系是第(7)种情况:粉色的圆系是第(4)种情况:蓝色的圆系是第(1)种情况:红色的圆系是第(9)种情况.

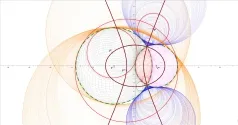
图4 动圆与定圆相切示意3

可以看到,两定圆相交时,动圆圆心轨迹互补的情况有椭圆(第(4)与第(7)种),双曲线(第(1)与第(9)种).

在图3中,双曲线只有右支.实际上,通过前面的论述发现,在图3中左支双曲线其实可以由两定圆相交时的第(2)种相切方法定义出,我们把左支双曲线在图3中补全,见图4.

图4中,圆P′′是第(2)种情况的动圆,橙色圆系是第(2)种情况的动圆圆系.

可以发现,这时,在两定圆相交的前提下,用动圆与两定圆相切,在有意义的不同相切方法组合中,我们定义出了完整的椭圆与双曲线.实际上,通过上面的讨论不难发现,只有在两定圆相交时才能完整地同时地定义出椭圆与双曲线.

至此,我们可以得出如下结论:

当两个大小定圆相交时,动圆的第(4)、(7)种相切方法,其圆心轨迹为椭圆:动圆的第(1)、(9)种相切方法,其圆心轨迹为双曲线右支,动圆的第(2)种相切方法,其圆心轨迹为双曲线左支.

这从另外一个角度揭示了椭圆与双曲线新的统一美.

(三)回顾与补充

①以上讨论,有R1＞R2的预设条件.其实,当R1=R2时,2a=R1-R2的第(1)、(2)、(8)、(9)种无法求得圆锥曲线轨迹(事实上,此时P点轨迹是直线),其余可行的情况中,两定圆位置关系也只能外离、外切、相交.

②本文最终只在最完美的情况—两定圆相交时下了结论,其实,两定圆不相交也能够定义出完整的椭圆或双曲线,只不过不能完整地同时地定义出罢了.