基于均匀化理论的两种网孔材料力学性能的比较

郑亚东，崔小朝，晋艳娟，张 柱

(太原科技大学应用科学学院，太原 030024)



基于均匀化理论的两种网孔材料力学性能的比较

郑亚东，崔小朝，晋艳娟，张 柱

(太原科技大学应用科学学院，太原 030024)

主要研究了网孔材料的力学性能。在均匀化理论的基础上，通过有限元软件ABAQUS计算了蜂窝孔材料和密排圆孔材料的等效弹性参数随实体率的变化规律，并提出两种网孔材料力学性能的比较分析。研究表明：当实体率相同时，密排圆形网孔的等效弹性模量和等效切变模量均大于蜂窝网孔。研究成果对工程实践中推广使用密排圆孔材料具有很大的价值。

网孔材料；均匀化理论；ABAQUS；等效弹性参数

随着材料科学的迅速发展，网孔材料成为科学领域所关注的重点，促进了建筑、汽车、造船、电信、机械等行业工程材料的发展。大多数工程材料具有非均匀化特点，这种非均性在某种程度满足人们对结构特殊功能的需求。经典的连续介质力学将研究对象看作是连续、均匀的材料。事实上，自然界中的材料本来就是非均匀的，连续材料只是在工程结构的宏观尺度范围内的理想化模型，而在细观尺度范围内，所有材料表现出其特有的非均匀性。非均匀材料由于其材质分布的不均匀性，导致其性能也是不均匀的，这是非均匀材料的主要特点[1]。由于非均匀材料的可设计、轻质等诸多优点，使得非均匀材料在工程结构中获得了日益重要的应用。王飞等在用均匀化理论分析蜂窝结构的等效弹性参数中利用均匀化理论探讨了蜂窝材料的等效弹性模量的计算方法，并与之比较了Gibson和W-K经验公式，指出了传统经验公式的不足[2]。刘书田等在基于均匀化理论的多孔板弯曲问题新解法中提出了多孔板弯曲问题的新的有限元解法[3]。樊学军在均匀化理论及其在生物力学中的应用中普及了均匀化理论的应用范畴[4]。本文将基于均匀化理论比较密排圆孔和蜂窝孔材料的等效弹性参数，进而帮助选择力学性能较优的材料。

1 均匀化理论及有限元法

1.1 均匀化理论

网孔材料是由单胞结构在平面内的周期性排列，如图1所示:

(a)整体结构 (b)单胞

Fig.1 Periodical structure diagram of mesh material

根据网孔材料的周期性特征，在外荷载的作用下，网孔单胞的场变量会随着宏观结构场变量的变化而变化。为描述结构在宏观及细观的场变量性质，引入小参数ε和宏观尺度 ：

y=x/ε

(1)

φε(x)=φ(x,x/ε)=φ(x,y)=φ(x,y+nY)

(2)

Y为此周期性函数的周期，对于一个单胞，式(2)关于xi求导为：

(3)

将周期性位移函数关于ε渐进展开得：

(4)

经过推导可得如下等效弹性模量的计算公式：

(5)

1.2 均匀化理论的有限元格式

为计算材料的等效弹性模量，需求出等效位移参数xmn(y).经推导得如下公式：

(6)

其中：

[Ke]=∫ΩeBTCBdV

(7)

2 周期性边界条件

代表性胞元上平均应力-应变关系满足均匀化理论的前提是：该代表性体积单元的边界必须施加周期性边界条件[5]。目前，均匀化理论中常见的边界条件有固支边界条件、等位移边界条件、周期性边界条件3种，其中周期性边界条件相对于其它两种边界条件来说是最为严格的边界条件[6]。任一代表性胞元的周期性边界条件为点、线分别满足不同的约束方程。

图 2 平面周期性单胞

Fig.2 Planar periodical cell

如图2所示，尺寸为2m*2n的代表性胞元共有两对边，两对边中每一对都需要符合如下的周期性边界条件：

(Ux=m-ux=-m)y=2me11

(8)

(vx=m-vx=-m)y=0

(9)

(wx=m-wx=-m)y=0

(10)

简化为：

UA-UB=δAB

(11)

(uy=n-uy=-n)x=2ne12

(12)

(vy=n-vy=-n)x=2ne22

(13)

(wy=n-wy=-n)x=0

(14)

简化为：

UC-UD=δCD

(15)

其中u、v、w分别表示x，y，z方向的位移，而对于该平面问题，w为0，e11,e22，e12是作用在代表胞元上的预应变，下标x=m，y=n表示对应边，下标y，x表示对应边上坐标相同的点。

上述方程定义了代表性单胞四个边的周期性位移边界条件，而单胞的四个顶点分别被相邻的两条边共享，因此仅仅依靠上述方程肯定会产生过约束。因此对于四个顶点也应当满足周期性边界条件，如下：

Ua-Ub=δAB

(16)

Uc-Ud=δAB

(17)

Ua-Uc=δCD

(18)

Ub-Ud=δCD

(19)

周期性边界条件需满足每一对边或点上的节点一一对应。为了确保每一个节点的对称性，一个单胞的网格部件是由1/4单胞相对于坐标轴镜像产生。因ABAQUS操作窗口中只能建立一点对一点，或者一点对多点的约束关系，而无法满足多点与多点一一对应，所以本文通过修改inp文件，对单胞结构施加相应的边界条件[7]。将周期性边界条件代入几何模型，经有限元软件分析得出等效位移参数x，然后将x代入式(5)进行数据处理，得到网孔材料的等效弹性矩阵，并由弹性矩阵与等效弹性模量的关系求出网孔材料的等效弹性模量。

3 基于ABAQUS的蜂窝网孔材料与密排圆孔材料力学性能的比较

对于网孔材料，针对不同类型的网孔材料，选取了相应的单胞。在此分析蜂窝网孔和密排圆孔的等效弹性常数。为满足均匀化理论，选取了图3所示的单胞结构作为蜂窝和密排圆型网孔的最小单胞结构进行分析[8]。

(a)蜂窝孔单胞

(b)密排圆孔单胞

图3 网孔材料单胞

Fig.3 Cells of mesh structure

根据前文所介绍的均匀化理论和周期性边界条件，我们选取不锈钢材料作为研究材料，其弹性模量E=206 Gpa，泊松比v=0.3，并通过ABAQUS软件分别模拟蜂窝材料和密排网孔结构的等效弹性参数。在有限元分析过程中我们通过施加X轴和Y轴方向的单位应变，以及面内的单位切向应变，确定单胞结构的位移场。当实体率为50%时，得到图4所示应力云图。其中(a)、(b)、(c)分别表示X轴向单位应变、Y轴向单位应变，XY面内单位切应变作用下蜂窝孔单胞和密排圆孔单胞的应力云图；而(d)、(e)、(f)分别表示X轴向单位应变、Y轴向单位应变，XY面内单位切应变作用下密排圆孔单胞的应力云图。比较两种网孔结构的应力云图，发现蜂窝结构与密排圆孔结构云图形状相似，不同的是蜂窝结构在拐角处出现明显的应力集中现象，而密排圆孔结构分布较为均匀，且圆弧位置处应力不存在突变。

图4 轴向应力云图

Fig.4 The axial stress cloud

在模拟过程中，通过调整实体率来研究网孔材料等效弹性参数的变化规律，并进一步研究网孔形状对网孔材料力学性能的影响。得到了如图5所示的两种网孔材料等效弹性常数随实体率的变化曲线。

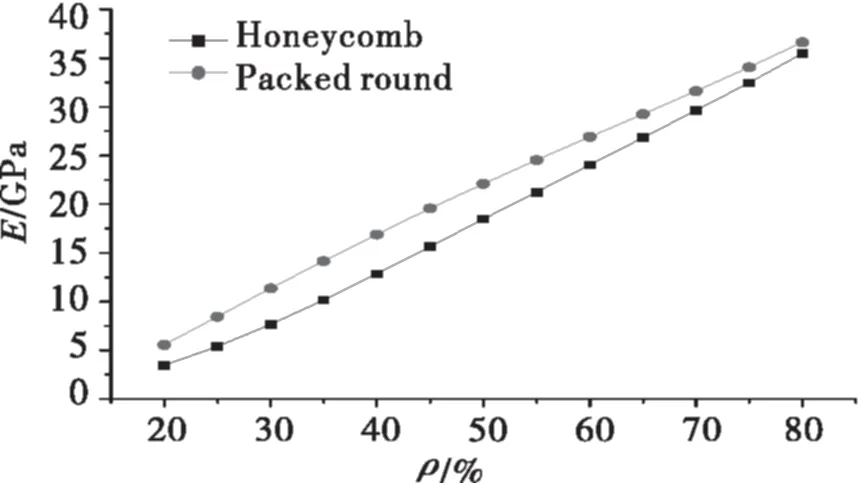
(a)蜂窝材料与密排圆孔材料等效弹性模量的拟合曲线

(b)蜂窝材料与密排圆孔材料等效切变模量的拟合曲线

图5 蜂窝材料与密排圆孔材料力学性能有限元结果的拟合曲线

Fig.5 The fitted curves of mechanical properties of honeycomb and packed round mesh material from numerical parameters

由图5(a)所示，密排圆孔结构等效弹性模量大于蜂窝结构的等效弹性模量，由图5(b)所示密排圆孔结构等效切变模量大于蜂窝结构的等效切变模量。因而当实体率相同时，圆孔密排结构的抗拉压性能与抗切变性能均要强于蜂窝结构。另外对于相同等效弹性模量的蜂窝孔材料和密排圆孔材料，后者具有较小的实体率，因而选择使用密排圆孔材料可以起到节省材料的作用，这是网孔材料轻质化的要求充分体现。在工程实践中，若网孔形状没有特殊需要，应当尽可能选取密排圆孔材料作为网孔材料。

4 结 论

(1)通过比较蜂窝孔单胞与密排圆孔单胞的应力云图及等效弹性参数，模拟结果表明，相同实体率的情况下，密排圆孔材料的等效弹性模量和等效切变模量均大于蜂窝孔结构。

(2)对于相同等效弹性模量的蜂窝孔材料和密排圆孔材料，后者具有较小的实体率，因而选择使用密排圆孔材料可以起到节省材料的作用。工程实践中，应当应当尽量选用密排圆孔材料。

[1] 黄富华．周期性复合材料有效性能的均匀化计算[D]．哈尔滨：哈尔滨工业大学，2010.

[2] 王飞．用均匀化理论分析蜂窝结构的等效弹性参数[J]．力学学报，2002，34(6)：915-916.

[3] 刘书田，程耿东，顾元宪. 基于均匀化理论的多孔板弯曲问题新解法[J]. 固体力学学报，1999，20(3)：195-196.

[4] 樊学军. 均匀化理论及其在生物力学中的应用[J].力学进展，1996，26(2)：187-188.

[5] 廖英强，刘勇琼．轴棒法炭/炭复合材料力学性能预测研究[J]．功能材料，2013，44(6)：878-879.

[6] 张超，许希武，严雪．纺织复合材料细观力学分析的一般性周期性边界条件及其有限元实现[J]．航空学报，2013，34(7)：1636-1638.

[7] 晋艳娟．碳-铝复合材料板带铸轧控制成型及力学行为研究[D]．太原：太原科技大学，2013.

[8] 周金翠．基于有限元模型的蜂窝芯层面内等效弹性模量仿真[J]．机械强度，2015，37(3)：488-492.

Comparison of Elastic Property of Two Kinds of Mesh Materials Based on Homogenization Theory

ZHENG Ya-dong, CUI Xiao-chao, JIN Yan-juan, ZHANG Zhu

(School of Applied Science, Taiyuan University of Science and Technology, Taiyuan 030024, China)

In this paper, the mechanical properties of mesh materials are studied. Based on the theory of Homogenization, the variation rule of honeycomb mesh material and packed round mesh material is calculated with the help of ABAQUS, and the comparative analysis of these two kinds of mesh material is put forward. The results show that when the entity rate is the same, the equivalent elastic and shear modulus of packed round mesh material are bigger than honeycomb mesh material. This result is valuable for the promotion of packed round mesh material in the engineering practice.

mesh materials, homogenization theory, ABAQUS, equivalent elastic modulus

1673-2057(2016)06-0486-05

2015-11-23

郑亚东(1991-)，男，硕士研究生，主要研究方向为材料断裂理论与结构设计。

国家自然科学基金(51574171)、山西省自然科学基金(2015011002，2015021021)、太原科技大学博士启动基金(20132012)

O341

A

10.3969/j.issn.1673-2057.2016.06.013