三孔小净距隧洞下穿既有铁路列车振动荷载动力响应研究

高 杰

(济南铁路局 建设项目管理中心，山东 济南 250001)



三孔小净距隧洞下穿既有铁路列车振动荷载动力响应研究

高 杰

(济南铁路局 建设项目管理中心，山东 济南 250001)

以下穿既有铁路的三孔小净距隧洞为工程背景，采用数值方法建立动力计算模型，分别研究初始正常行车工况、初期支护正常行车工况和初期支护慢行工况条件下，列车动荷载作用下路基、围岩和初期支护的应力和位移响应。研究结果表明：列车振动不可避免地对正在施工的隧洞产生不利影响，使初期支护产生一定的附加沉降和附加应力，采取加固措施和限速慢行可有效地减小动荷载产生的不利影响。

隧洞；列车动荷载；初期支护；动力响应

0 引言

随着各种基础设施建设的大力发展，各种工程间近接施工相互影响越来越显著。其中新建隧道(洞)下穿既有铁路施工中，铁路正常运营不允许被中断，隧道(洞)施工不可避免地会对既有铁路路基产生扰动，列车振动进一步加剧正在施工隧道(洞)扰动变形，影响到既有铁路的安全运营和隧道(洞)自身施工安全。关于列车荷载一直是一个难以处理的问题，为此国内外学者作了大量的工作，主要集中在地铁与普通铁路列车荷载的模拟研究[1-4]。另外针对下穿既有铁路列车振动荷载动力响应也开展了大量研究工作[5-8]。

南水北调中线以隧洞方式下穿京九铁路，隧洞断面形式为分离式小净距三孔暗挖隧洞形式。每孔断面形式最大跨度为7.5 m，高9.95 m。每两孔中间净土柱宽度10 m。隧道拱顶至地面最小高度仅为1.69 m，距铁路路肩高度为4.33 m。工程区域内主要位于粉、细、中砂层。围岩土体松散、自稳能力差、易坍塌，结构上方铁路线列车行车频繁，路基振动大，隧道开挖多次扰动有可能导致铁路路基沉降超标，影响既有线设备的正常运营。

通常考虑铁路路基设计荷载时，在计算中常把静荷载和动荷载一并简化为静荷载处理，即换算土柱法。本工程中由于三孔隧洞的施工是在不中断行车的情况下进行，故对于隧洞的初期支护结构不仅应进行静荷载分析，还应进行列车动荷载的分析，应考虑列车动荷载作用下路基、围岩及初期支护结构所产生的动应力的大小和分布规律。

1 列车荷载

列车荷载是一个很复杂的问题，同时涉及到车辆轴重、悬挂质量、列车运行速度、轨道形式、线路平顺度等多方面因素。当采用无缝线路时，影响轮轨力的主要原因是轨道不平顺和轨面磨损效应。

用一个激励力函数来模拟列车荷载，其中包括静力荷载和一系列正弦函数叠加而成的动荷载，表示为

式中，k1为相邻轮轨力的叠加系数，一般取值为1.2～1.7；k2为钢轨分散系数，一般为0.6～0.9；P0为车轮静载；P1为对应于按列车平衡性控制的某一典型值的振动荷载；P2为对应于按作用到线路上动力附加运载控制的某一典型值的振动荷载；P3为对应于按波形磨损控制的某一典型值的振动荷载。

令列车簧下质量为M0，则相应的振动荷载幅值为

(2)

式中，M0为簧下质量；ai为相应于不平稳控制条件下的几何不平顺矢高，反映了路况；ωi为振动圆频率，其表达式为ωi=2πv/Li，其中，v为列车的行车速度，Li为几何不平顺曲线的波长。

目前国内机车质量一般为132 t，一般为两个轴向架6轴，轴重为22 t，取单边静轮重110 kN，簧下质量M0为750 kg，对应于P1、P2、P33种控制条件分别取其典型的不平顺振动波长和相应的矢高分别为：L1=10 m，a1=3.5 mm；L2=2 m，a2=0.4 mm；L3=0.5 m，a3=0.08 mm。取v=200 km/h，取前2.0 s的情形。此外，k1，k2可根据车辆类型和轨道结构轴重、长度、列车运行速度以及钢轨和轨枕类型等条件计算而得。本工程中k1取1.5，k2取0.7。将以上各值带入式(1)、(2)可得到列车时速120 km/h(33.33 m/s)及45 km/h(12.5 m/s)，运行2 s的列车荷载时程曲线如图1所示。

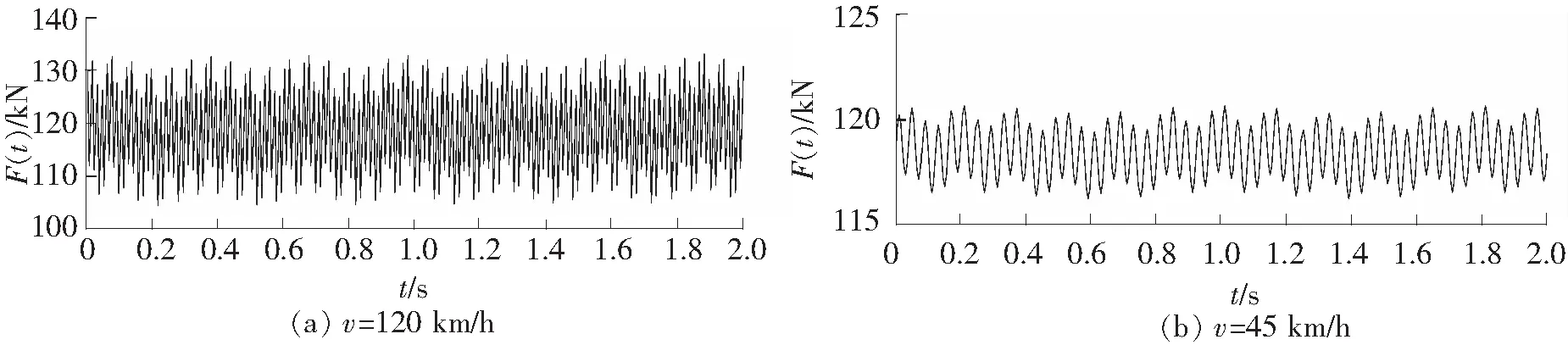
图1 列车移动荷载时程曲线

2 动力计算模型

在三维静力模型基础上，考虑初期支护施工完成后路基和隧洞初期支护的位移及初期支护受力在列车荷载作用下的动力响应。模型边界通过前、后、左、右及底面建立曲面弹簧实现。动力荷载考虑单侧行车情况下的列车荷载。曲面弹簧的地基反力系数利用铁路设计规范的地基反力系数计算。

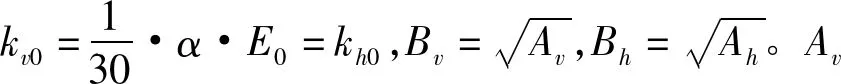
为模拟随列车移动荷载的动力分析，利用吸收边界代替弹簧来定义边界条件，为了定义吸收边界在相应的地基特性值的x、y、z方向输入阻尼。阻尼计算如下。

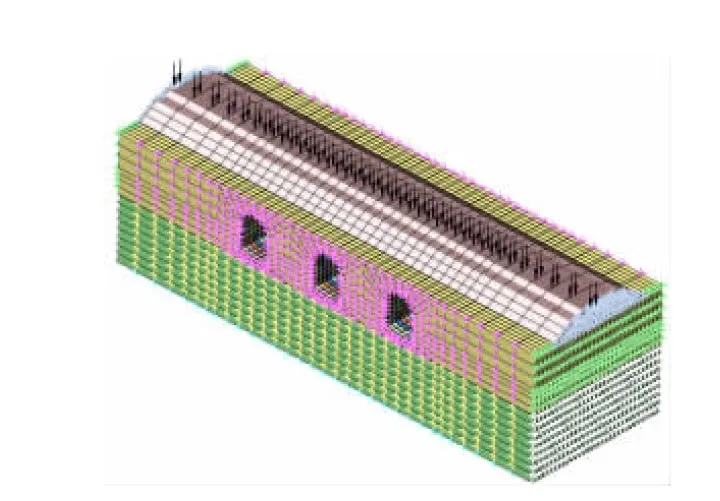
图2 动力计算模型

P波：

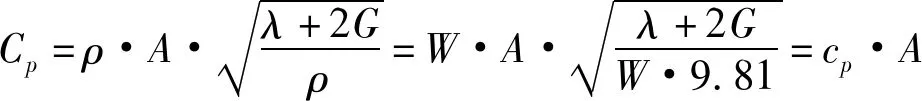
S波：

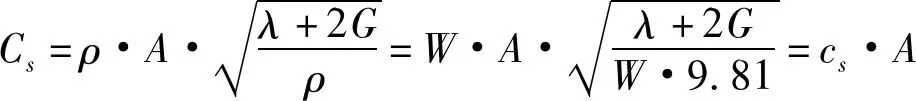
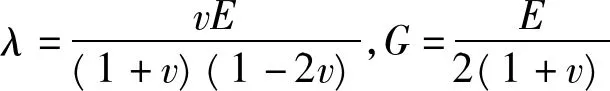
其中，E为材料的弹性模量，ν为泊松比，A为截面积。

计算模型如图2所示。

3 计算结果

3.1 初始正常行车工况(未开挖隧洞)(v=120 km/h)

考虑列车行车速度120 km/h，机车进入模型区间的时间约为1 s，通过模型区间的时间约为4 s，故分别提取1 s、2.5 s、4 s时刻的竖向位移结果如图3所示。分别在中洞上方路基中线和路肩设监测点，可得路基中线和路肩的沉降及沉降速度的时程曲线如图4所示。

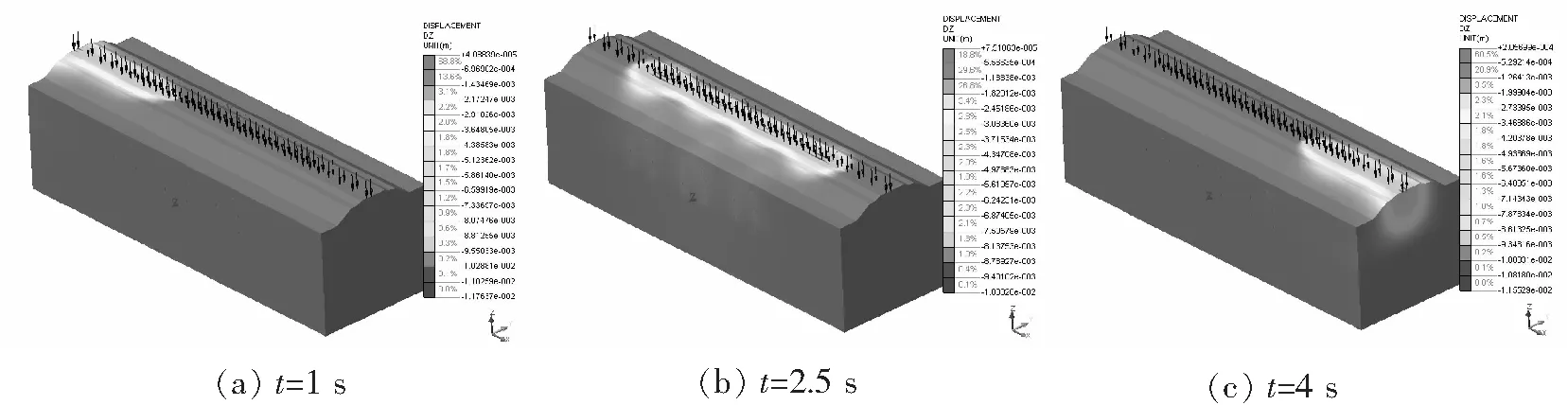
图3 初始阶段不同时刻路基竖向位移分布

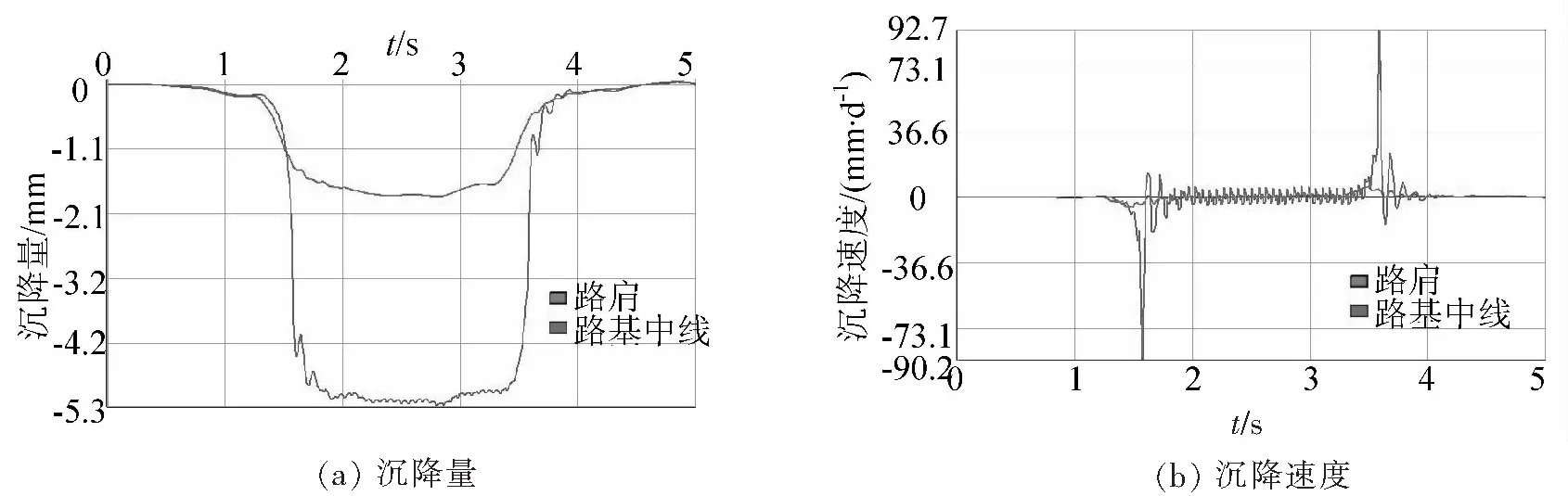
图4 初始阶段路基中线及路肩沉降及沉降速度时程曲线

由图3和图4可知，路基在机车进入区间(t=1 s)、机车行进过程(t=2.5 s)、机车驶离区间(t=4 s)时刻的最大竖向位移分别为1.176 cm、1.003 cm、1.155 cm。路基下沉最大值均出现在列车动荷载作用点部位。路基中线位置最大下沉量为5.229 mm，最大下沉速度9.265 cm/s。路肩位置的下沉量及下沉速度较荷载作用点及路基中线要小得多。

3.2 隧洞初期支护正常行车工况(v=120 km/h)

考虑列车行车速度120 km/h，机车进入模型区间的时间约为1 s，通过模型区间的时间约为4 s，故分别提取1 s、2.5 s、4 s时刻的路基竖向位移分布结果如图5所示，三孔隧洞的竖向位移分布如图6所示。分别在中洞上方路基中线、路肩、隧洞拱顶设监测点，可得路基中线和路肩的沉降及沉降速度的时程曲线如图7所示，三孔隧洞初期支护拱顶下沉及拱顶下沉速度时程曲线如图8所示。

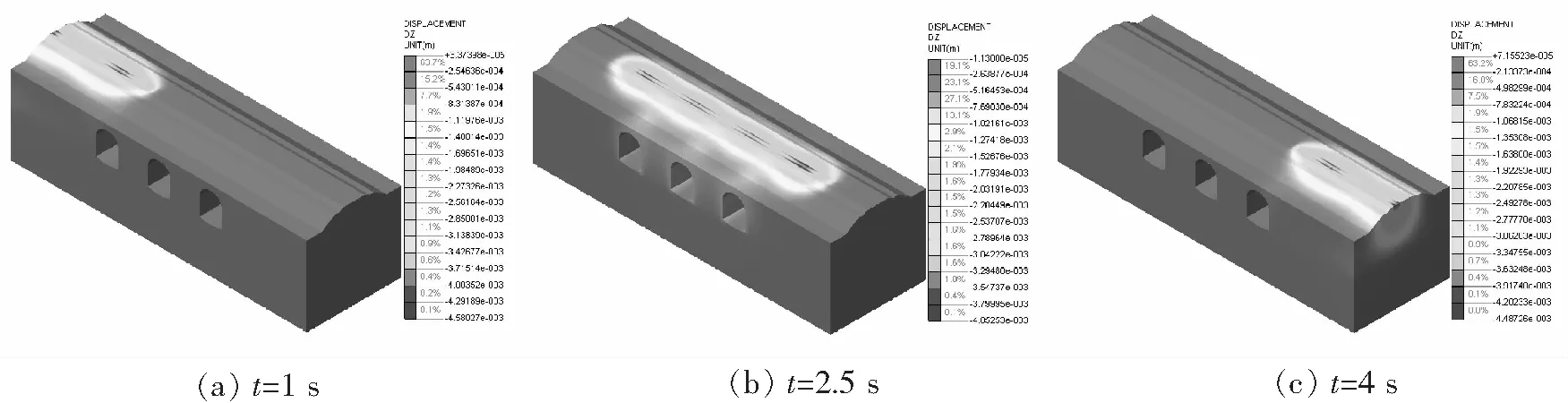
图5 初期支护阶段不同时刻路基竖向位移分布

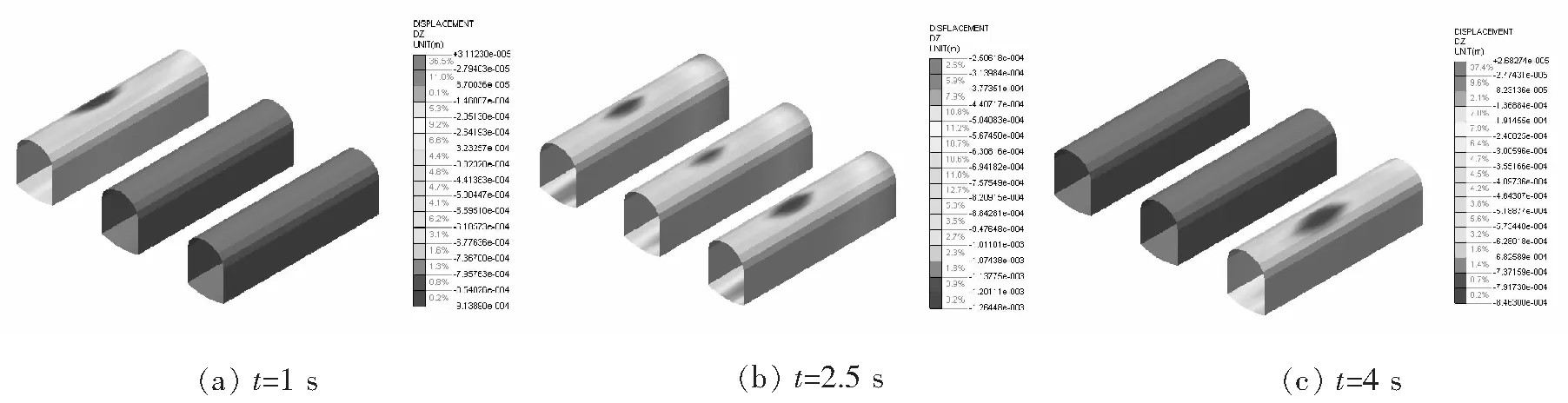
图6 初期支护阶段不同时刻隧洞初期支护竖向位移分布

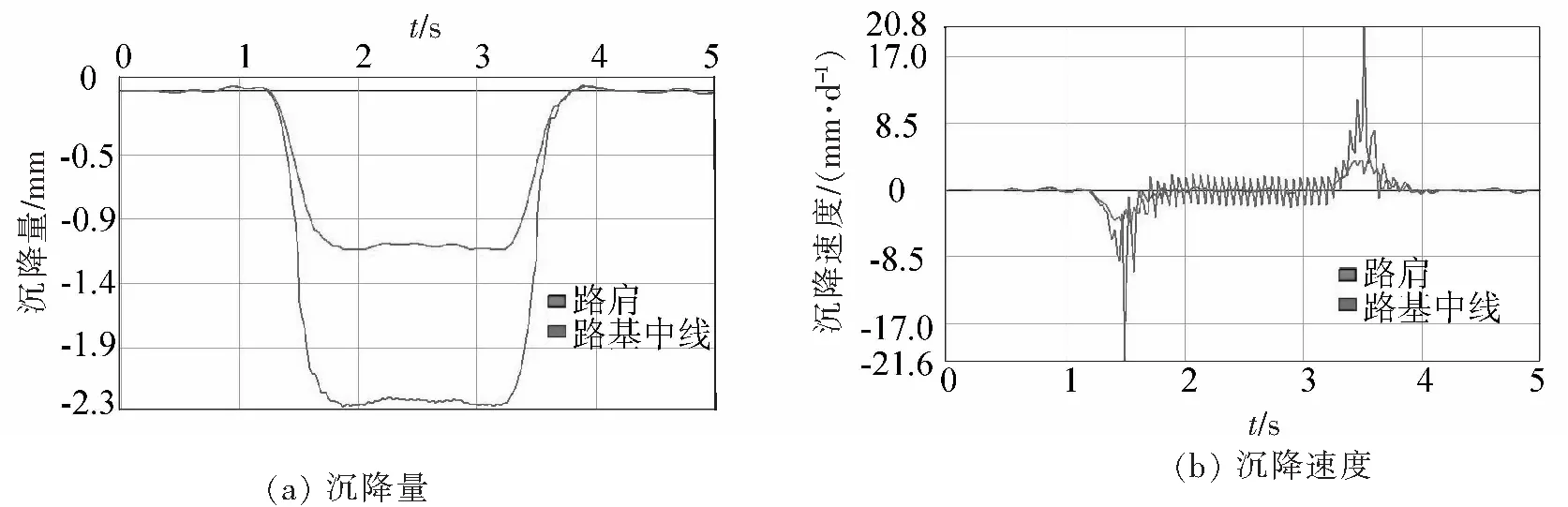
图7 初期支护阶段路基中线及路肩沉降及沉降速度时程曲线

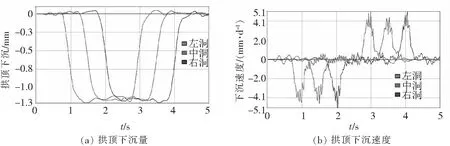
图8 初期支护阶段三孔隧洞拱顶下沉速度时程曲线

由图5～图8可知，路基在机车进入区间(t=1 s)、机车行进过程(t=2.5 s)、机车驶离区间(t=4 s)时刻的最大竖向位移分别为4.580 mm、4.053 mm、4.487 mm。相应时刻的三孔隧洞初期支护最大竖向位移分别为0.855 mm、1.264 mm、0.846 mm。路基下沉最大值均出现在列车动荷载作用点部位，初期支护最大竖向位移出现在列车动荷载作用点下方拱顶部位。路基中线位置最大沉降量为2.28 mm，最大沉降速度2.16 cm/s。路肩位置的下沉量及下沉速度较荷载作用点及路基中线要小得多。三孔隧洞中心监测点最大拱顶下沉1.250 mm，最大拱顶下沉速度5.107 mm/s。中洞初期支护最大附加拉应力0.091 MPa，最大附加压应力0.576 MPa。

3.3 隧洞初期支护慢行工况(v=45 km/h)

考虑列车行车速度45 km/h，机车进入模型区间的时间约为2.2 s，通过模型区间的时间约为7.8 s，故分别提取2.2 s、5.6 s、7.8 s时刻的路基竖向位移结果如图9所示，三孔隧洞的竖向位移分布如图10所示。分别在中洞上方路基中线、路肩、左洞拱顶、中洞拱顶及右洞拱顶设监测点，可得路基中线和路肩的沉降及沉降速度的时程曲线如图11所示，三孔隧洞初期支护拱顶下沉及拱顶下沉速度时程曲线如图12所示。

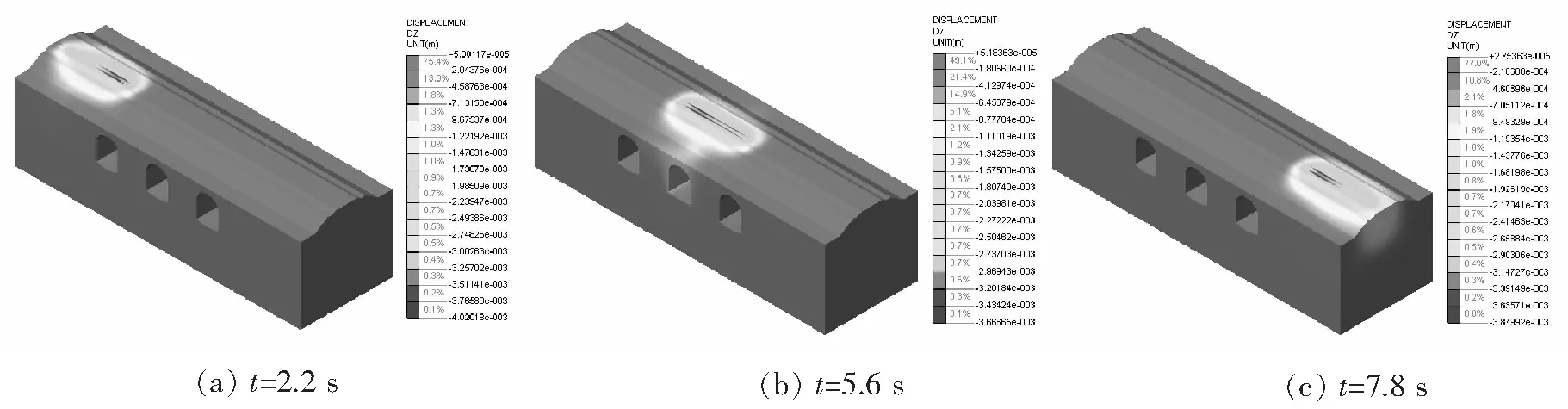
图9 初期支护慢行阶段不同时刻路基竖向位移分布

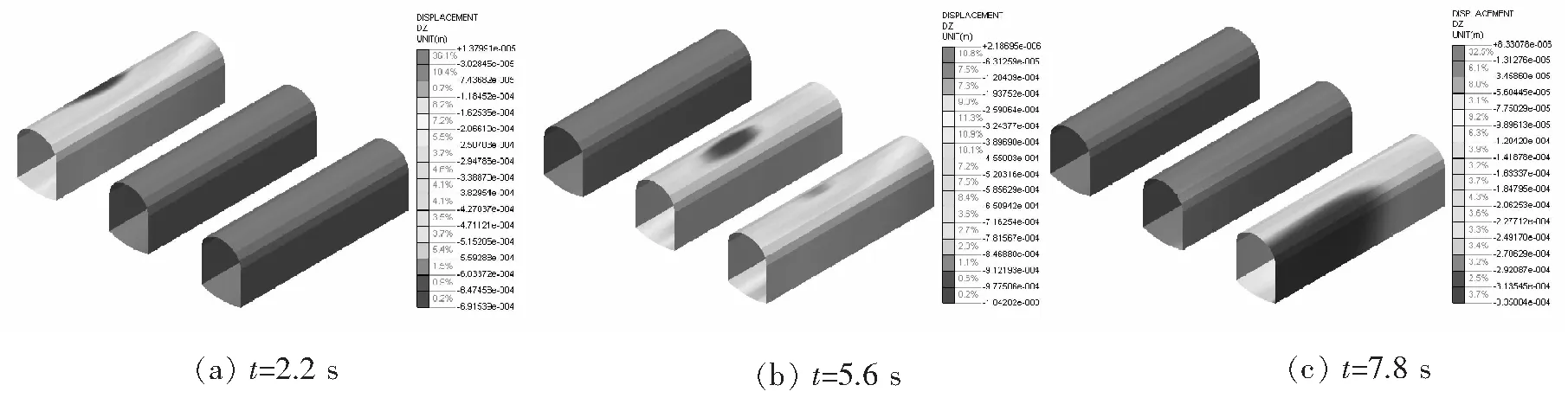
图10 初期支护慢行阶段不同时刻隧洞初期支护竖向位移分布

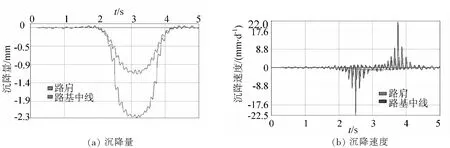
图11 初期支护慢行阶段路基中线及路肩沉降及沉降速度时程曲线

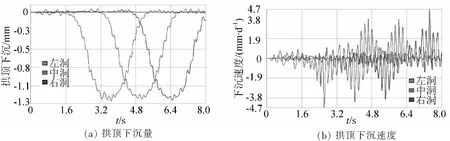
图12 初期支护慢行阶段三孔隧洞拱顶下沉速度时程曲线

由图9～图12可知，路基在机车进入区间(t=2.2 s)、机车行进过程(t=5.6 s)、机车驶离区间(t=7.8 s)时刻的最大竖向位移分别为4.020 mm、3.667 mm、3.880 mm。相应时刻的三孔隧洞初期支护最大竖向位移分别为0.692 mm、1.043 mm、0.335 mm。路基下沉最大值均出现在列车动荷载作用点部位，初期支护最大竖向位移出现在列车动荷载作用点下方拱顶部位。路基中线位置最大沉降量为2.29 mm，最大沉降速度2.24 cm/s。路肩位置的下沉量及下沉速度较荷载作用点及路基中线要小得多。三孔隧洞中心监测点最大拱顶下沉1.260 mm，最大拱顶下沉速度4.747 mm/s。中洞初期支护最大附加拉应力0.093 MPa，最大附加压应力0.607 MPa。

3.4 不同工况条件动力响应结果分析

比较3种工况条件下路基及隧洞初期支护由于列车动荷载作用而引起的附加竖向位移和初期支护附加应力，列于表2。

表2 不同工况条件下路基及初期支护附加竖向位移及附加应力

由表2可知，比较隧洞施工前后路基竖向位移的动力响应，在隧洞开挖并施作初期支护后，路基最大竖向位移明显减小，这与初期支护施作后提高了区域整体刚度有关。比较初期支护阶段快行(120 km/h)和慢行(45 km/h)工况路基和初期支护附加竖向位移和附加应力，列车限速慢行(45 km/h)条件下，路基及初期支护最大竖向位移可下降20%左右，监测点时程曲线中竖向位移及初期支护附加应力的数值相当，变化不明显。

4 结语

在不中断行车条件下，列车振动不可避免地对正在施工的隧洞产生不利影响，使初期支护产生一定的附加沉降和附加应力。采取加固及施工辅助措施提高影响区域整体刚度，对减小列车荷载的动力附加位移是非常有效的，限速慢行也可较为有效地减小动荷载产生的不利影响。

[1]潘昌实，G.N.Pande. 黄土隧道列车动荷载响应有限元初步数定分析研究[J].土木工程学报,1984，17(4):19-28.

[2] 甘惠琳，曹雪琴.车速提高对桥梁竖向振动影响的随机模拟分析[J].上海铁道学院学报，1990,11(4):45-53.

[3] 李军世，李克钏.高速铁路路基动力反应的有限元分析[J].铁道学报，1995,17(1):66-75.

[4] 梁波，罗红，孙常新. 高速铁路振动荷载的模拟研究[J].铁道学报，2006,28(8):89-94.

[5] 高玄涛. 高速铁路列车振动荷载对下穿隧道地层动力响应分析[J]. 铁道标准设计，2014，58(6):93-97.

[6]王庆浩，钱德玲，佟国锋. 高速列车振动荷载作用下交叠隧道结构动力响应分析[J].兰州工业学院学报2015,22(4):1-5.

[7] 边学成. 高速列车运动荷载作用下地基和隧道的动力响应分析[D].杭州：浙江大学，2005.

[8] 丁祖德. 高速铁路隧道基底软岩动力特性及结构安全性研究[D].长沙：中南大学，2012.

Dynamic Response of Three Pipes Small Spacing Tunnels Under Train-induced Dynamic Load

Gao Jie

(Construction Project Management Center of Jinan Railway Bureau, Jinan 250001, China)

Based on three pipes small spacing tunnels underneath existing railway, the dynamic response of roadbed and ground and primary support is studied by numerical method. The calculated work conditions of dynamic analysis model include initial normal driving speed condition, primary-support normal and driving-speed condition and primary-support slow driving-speed condition. The results show that the train vibration inevitably brings adverse effect to construction tunnel, and causes additional displacement and stress to the primary support. The adverse effect can be reduced by adopting reinforcement measures of ground and slow driving speed of train.

tunnel; train-induced dynamic load; primary support; dynamic response

2015-12-21 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2016.02.08

高杰(1984-)，男，工程师，主要从事土木工程技术管理工作，E-mail:290661790@qq.com

U213.1

A

2095-0373(2016)02-0039-06

高杰.三孔小净距隧洞下穿既有铁路列车振动荷载动力响应研究[J].石家庄铁道大学学报:自然科学版,2016,29(2):39-44.