基于随机共振的齿轮箱早期故障诊断研究

杨红娜， 郝如江

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)



基于随机共振的齿轮箱早期故障诊断研究

杨红娜， 郝如江

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

随机共振在微弱故障诊断中相对线性系统具有明显优势，能显著增强信号的信噪比。将随机共振与共振解调相结合来检测齿轮箱的早期裂纹故障，首先通过带通滤波选取共振频带，然后通过Hilbert进行解调，最后采用归一化方法调节随机共振的系统参数得到故障特征输出。对仿真信号和QPZZ-Ⅱ齿轮故障系统实测数据的处理结果表明，该方法与传统共振解调相比具有明显优势，为齿轮箱故障诊断提供了一种更为有效的途径。

共振解调；随机共振；齿轮箱；故障诊断

0 引言

城轨列车以其安全、稳定、高效的运行方式使之成为现代城市公共交通的一种重要形式，其安全稳定地运行直接影响到城市生活的质量和秩序。齿轮箱是列车动力传动的核心部件，其运行的安全性和可靠性是影响列车安全运行的重要因素。

齿轮失效主要发生在轮齿，原因有过载、疲劳、点蚀和胶合等，其中疲劳破坏是常见的一种破坏形式。众所周知，疲劳破坏具有以下特点：破坏时没有明显的宏观塑性变形，断裂前没有预兆而是突然发生；引起疲劳断裂的应力很低，常常低于材料的屈服点。这就说明，将大量的研究工作放在显著故障的诊断研究，对于齿轮的疲劳破坏研究意义不大。齿轮的故障信号由调制的故障特征信号和背景噪声组成，在早期故障信号中，相对强大的背景噪声降低了信噪比，使早期的故障特征很难被检测出来。

基于线性系统的微弱信号检测技术，可以在一定程度上提高信噪比，但是它们的着眼点都集中在抑制噪声这一点上[1]，并且采用线性方法不能滤除与信号同频的噪声，只能通过提高采样频率，延长采样时间来解决。随机共振弥补了线性系统的不足，它是通过一个非线性系统将噪声的部分能量转化为信号的能量，从而增强信号特征的输出。经过多年的研究，随机共振技术已经在一些领域，比如微弱化学信号检测和转子碰摩故障信号早期检测中已有应用[2-3]。在城轨列车齿轮箱齿轮裂纹的早期故障检测中，采用共振解调与随机共振相结合的方法，从强背景噪声中提取出故障特征信号，为城轨列车齿轮箱状态监测，及早发现故障信息提供了一种新的思路。

1 随机共振检测微弱信号的原理及模型

随机共振(Stochastic Resonance, SR)理论最初是由Benzi等人在1981年提出的[4-5]，用来解释地球每隔10万年左右交替出现冰川期与暖气候期的现象。近30年来，随着非线性动力学和统计物理理论的发展，随机共振成为一种用于增强检测微弱特征信号的新方法[6-8]。

受外力和噪声共同作用的双稳态系统随机共振模型可以由Langevin方程(LE)描述，即

式中，V(x)为非线性双稳态势函数，且

式中，s(t)为外力；Γ(t)是强度为D、均值为0的高斯白噪声。

经典的随机共振只能检测故障频率在1Hz以下的故障特征，即所谓的近似绝热条件。对于机械故障诊断，故障信号一般都不满足近似绝热的条件。鉴于随机共振在微弱信号检测中的优良特性，近些年来众多学者进行了诸多尝试来突破近似绝热条件，比如归一化[9]、变步长法[10]、二次采样[11]、调制法[12]等都取得了一定研究成果。

由于实际信号的复杂性、噪声的多样性等，随机共振的各种参数调节方法整体还是处于探索和模糊期，规律不明显，参数可“移植”性差。在对比了以上方法的基础上认为，归一化方法相对于其它方法理论基础较好，参数调节方向相对清晰且有依据[13]，故对于齿轮箱故障信号的处理采用归一化方法来调节系统参数。

由于式(1)是一种非线性微分方程，并不存在精确解的表达式，因此采用四阶Runge-Kutta数值求解算法，算式如下

式中，sn和xn分别为输入信号s(t)和输出x(t)的第n个采样值。

2 基于随机共振的故障诊断流程

由于随机共振理论受近似绝热条件的限制，而实际齿轮信号又常与更高频率的机械固有频率发生调制，使随机共振算法的应用受限。因此本文提出在随机共振算法前添加共振解调环节降低信号频率，然后采用随机共振算法增强系统输出。具体流程如图1所示。

图1 故障处理流程

3 齿轮箱故障仿真算例

正常运行的齿轮，其振动信号主要包含齿轮啮合频率成分及其高次谐波成分，正常齿轮振动信号的表达式为

式中，N为啮合频率的最大阶数；fz为啮合频率；An为第n阶啮合频率的幅值；Φn为第n阶啮合频率的初始相位。

当齿轮出现故障时，在齿轮的啮合传动过程中，其振动信号中会产生幅值调制和频率调制现象。此时，齿轮的振动信号表达式为

式中，an(t)为第n阶啮合频率的幅值调制函数；bn(t)为第n阶啮合频率的相位调制函数(也称频率调制函数)。在齿轮的幅值调制和频率调制中，其调制频率为故障所在轴的转频及其倍频，因此，式(5)可转化为

式中，M为最大调制阶数；Bm为第m阶转频调制的幅值调制系数；fn为转频，fz=T·fn，T为齿轮齿数；βm为第m阶转频调制的频率调制系数。

在不影响分析效果的情况下，取仿真信号x=(1+0.5cos(2π×40×t))×cos(2π×600×t)，故障频率为40 Hz，载波频率为600 Hz。图2为该仿真故障齿轮振动信号的时域波形。

为验证随机共振对微弱故障特征的识别能力，现对仿真信号添加幅值为5的强噪声，x=(1+0.5cos(2π×40×t))×cos(2π×600×t)+5×rand(size(t))。其时域波形如图3，故障特征被完全淹没在噪声中。

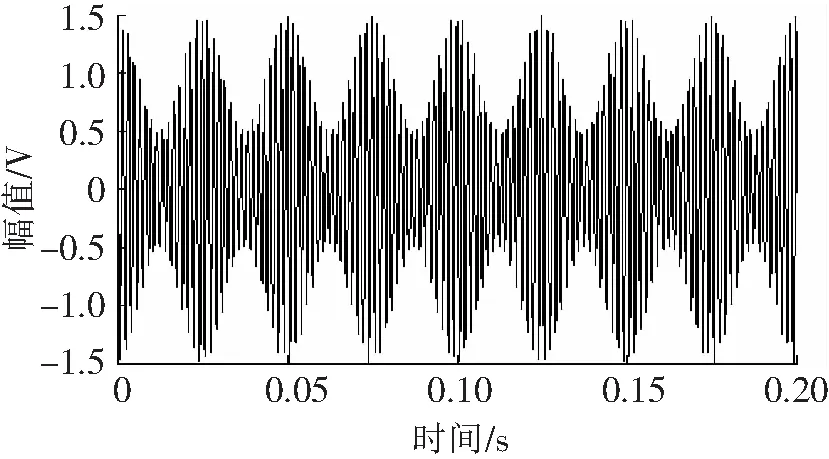
图2 仿真信号时域波形

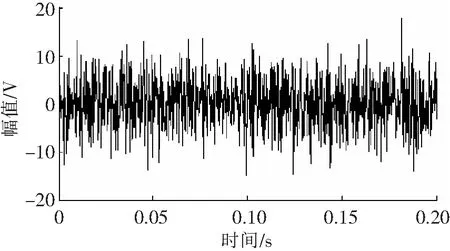
图3 仿真信号加噪后的时域波形

分别用传统的共振解调方法与包络解调加随机共振两种方法进行分析，对比处理后的结果如图4所示。

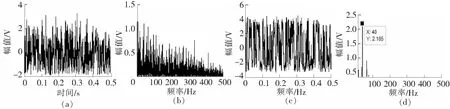
图4 仿真信号处理结果

图4(a)是仿真信号经过共振解调后的时域波形；图4(b)是图4(a)的频谱图；图4(c)是图4(a)经过随机共振处理后的时域波形；图4(d)是图4(c)的频谱图。由图4可知，在强噪声弱信号的检测中，传统的共振解调完全失效的情况下，随机共振显示出明显的优势，能明显地检测出故障特征。

4 齿轮箱故障特征提取

为了验证随机共振方法提取微弱故障模式的有效性，设计模拟了城轨列车齿轮箱故障实验。图5是QPZZ-Ⅱ型齿轮箱故障试验台，其中模拟的故障齿轮单齿齿根裂纹深度为0.5 mm。

测试工况时电机转频为12.1 Hz，传感器安装在齿轮箱箱体上，采样频率10 kHz，采样时间长度为6.4 s。齿轮齿数及计算得到的大小齿轮的转频如表1所示。实测信号时域波形见图6。

表1 齿轮参数

图5 试验台

图6 实测信号时域波形

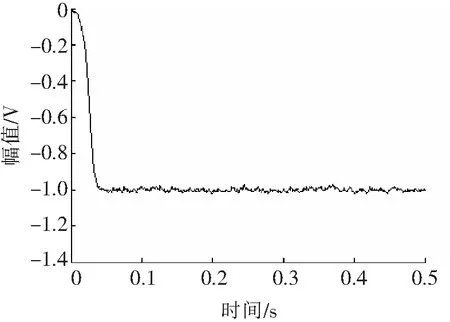
图7 SR系统在初始化参数下输出

根据理论分析，齿轮发生裂纹时，会产生频率等于齿轮转频的特征信号，但是在早期裂纹故障信号中，特征信号较弱，加上复杂的工作环境，使得信号的信噪比很低。用SR的方法对采样数据进行特征提取，在不了解信号特征的情况下用归一化的方法初始化参数，取a=165,b=165，步长为采样频率的倒数，信号能量放大165倍。分析结果如图7所示。

图7中，信号初始点在0，最后稳定在-1左右，并没有出现0线上下呈规律性的循环信号。原因分析如下：

(1)参数分析。参数设置参照文献[14]的归一化方法，a、b、h和采样频率符合归一化思想。

(2)根据文献[14]的介绍，归一化方法下参数选择需要满足下式才能达到稳定性的要求：

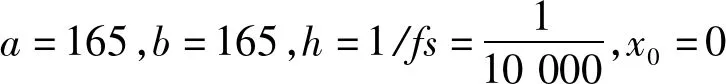
参数设置满足稳定性要求。

(3)用势函数的思想分析原因。势垒高度太大，质点处于一侧势阱内没有办法完成跃迁。解决办法为降低势垒的高度[15]。

对于以上参数设置完全满足归一化和稳定性要求，但是在实测信号中却没有得到理想输出的问题,有些学者已经对此问题进行过讨论，比如文献[16]中就提出对于高频周期信号，通过改变双稳系统参数很难达到稳定输出。出现该问题的原因是多方面的，最主要的是实测信号中存在各种机械误差，噪声成分比较复杂,因此归一化方法在实测信号中的应用仍有待深入研究。

针对以上问题，本文采用第三条解决办法处理系统稳定的问题，调节的值使势垒高度降低，选取a=5,b=300 000使系统得到稳定输出如图8所示。

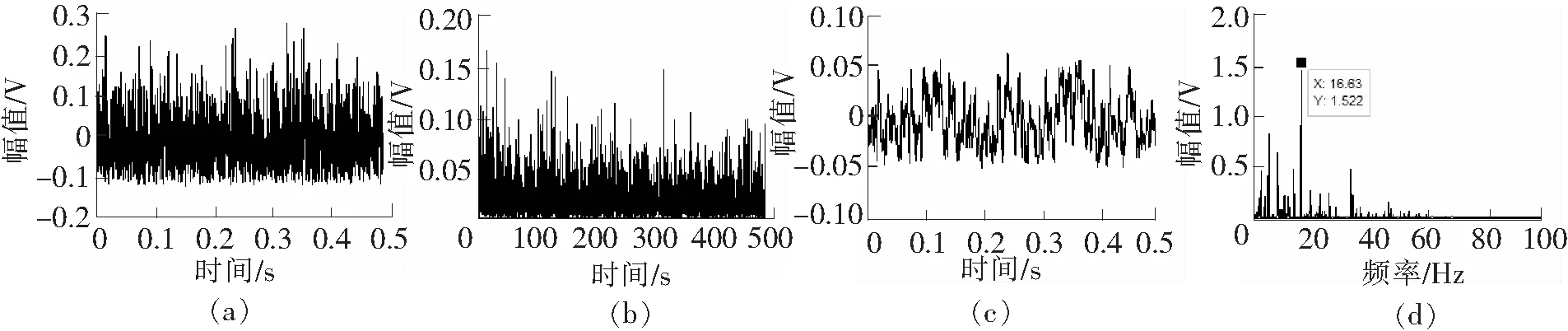
图8 实验数据计算结果

图8(a)是采集信号经过共振解调后的时域波形；图8(b)是图8(a)的频谱图。图8(b)中无明显的故障特征频率成分，信号能量处于近似均匀分布状态。包络解调后的信号经过非线性SR系统得到图8(c)的信号，将图8(c)与包络解调后的信号图8(a)做对比，图8(a)信号杂乱密集无明显周期成分，图8(c)信号规律性初显，隐约可以分辨出周期成分，可见SR系统将部分噪声能量转移给了周期成分，噪声得到抑制。图8(d)是信号图8(c)经傅氏变换得到的，峰值频率16.63 Hz，与小齿轮的转频16.5 Hz接近，峰值明显，计算结果与实际情况相符。

对比图8(b)、图8(d)，经SR系统后信号能量整体向低频段转移，高频信号得到抑制，明显增强了低频周期信号的能量。在图8(d)中噪声成分得到抑制，但是除16.63 Hz的峰值外会随机出现一些幅值次于峰值但很明显的小峰值，主要原因可能有两个方面：第一，实采信号的噪声成分远比理想化的白噪声复杂；第二，信号特征微弱，随机出现的一些次峰值说明噪声处于重要地位不能完全抹去。

5 结论

归一化参数调节方法相对其它方法理论基础更好，但是在处理实测信号时很难得到理想的输出，需要在归一化的基础上进一步调节系统参数，这个过程可能会花费很多时间，因此单一的归一化方法在处理工程实际信号时受到一定限制。鉴于随机共振在微弱信号检测方面的显著优势，提出在接下来的研究中，应在合理的采样频率的基础上，系统的研究a,b,h三个参数对系统输出的影响，为随机共振系统稳定性调节提供更好的依据。

针对基于随机共振算法的齿轮箱早期裂纹故障检测问题，利用四阶龙格库塔算法，归一化参数调节机制，对齿轮箱早期故障进行了数值仿真和实验数据的检测验证。将计算结果分别与传统的共振解调相对比，结果表明，基于随机共振算法的早期故障检测要明显优于共振解调结果。通过对比研究的方法在强噪声背景下提取齿轮箱微弱信号的研究对微弱信号的增强与检测具有一定的理论指导意义与实用价值。

[1]Asdi A S,Tewfik A H. Detection of weak signals using adaptive stochastic resonance[C]//Proceeding of the 1995 IEEE International Conference on Acoustics, Speech, and Signal Processing.[S.l.]:[s.n.]，1995: 1332-1335.

[2]王利亚, 蔡文生, 印春生,等. 一种有效提取弱信号的新方法[J]. 高等学校化学学报, 2000，21(1) : 53-55.

[3]胡茑庆, 陈敏, 温熙森. 随机共振在转子碰摩故障早期检测中的应用[J]. 机械工程学报, 2001，31(9) : 88-91.

[4]Benzi R, Sutera A,Vulpiana A. The mechanism of stochastic resonance[J]. Journal of Physics A :Mathematical and General, 1981,14:453-457.

[5]Benzi R, Parisi G, Sutera A,et al. A theory of stochastic resonance in climatic change[J]. SIAM J.APPL.MATH.,1983,43(3):565-578.

[6]夏均忠,刘远宏,马宗坡,等.基于调制随机共振的微弱信号检测研究[J].振动与冲击,2012,31(3):132-135.

[7]韩东颖,丁雪娟,时培明.基于自适应变尺度频移带通随机共振降噪的EMD多频微弱信号检测[J].机械工程学报,2013,49(8):10-18.

[8]雷亚国,韩冬,林京,等.自适应随机共振新方法及其在故障诊断中的应用[J].机械工程学报,2012,48(7):62-67.

[9]张晓飞,胡茑庆,胡雷,等.基于倒谱预白化和随机共振的轴承故障增强检测[J].机械工程学报,2012,48(23):83-89.

[10]李强,王太勇,冷永刚,等.基于变步长随机共振的微弱信号检测技术[J].天津大学学报,2006,39(4):432-437.

[11]冷永刚,王太勇.二次采样用于随机共振从强噪声中提取弱信号的数值研究[J].物理学报,2003,52(10):2438-2442.

[12]明廷锋,龙景兵,张永祥.大参数条件下周期信号的三种随机共振检测方法[J].测试技术学报,2014,28(6):476-480.

[13]刘利姣,黄光明,杜茜,等.大参数随机共振的两种方法及数值仿真[J].信息与电子工程,2007,5(3):182-185.

[14]胡茑庆.随机共振微弱特征信号检测理论与方法[M].北京:国防工业出版社,2012.

[15]杨颖娜.基于随机共振算法的高速机车轮对滚动轴承故障信号检测[D].石家庄:石家庄铁道大学,2014.

[16]冷永刚,王太勇,郭焱,等.双稳随机共振参数特性的研究[J].物理学报,2007,56(1):30-35.

Research on Early Fault Diagnosis of Gearbox Based on Stochastic Resonance

Yang Hongna， Hao Rujiang

(School of Mechomical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

Stochastic resonance has obvious advantages in weak fault diagnosis for linear system, since it can significantly enhance the signal to noise ratio. In this paper, the stochastic resonance is combined with the resonance demodulation to detect early crack fault of the gearbox. The band-pass filter was selected by the resonant frequency band, then the Hilbert enveloping demodulation was used for the filtered signals, and finally the normalized stochastic resonance method by means of adjusting system parameters was applied to get the ideal characteristic output for the gearbox faults. Compared with the traditional resonance demodulation, simulated signals and QPZZ-II Gear fault system measured data were processed and analyzed, and the results show that the stochastic resonance method for the gearbox fault diagnosis is effectual for the weak signal detection and it provides a novel way for the default diagnosis for the rotational machines.

resonance demodulation; stochastic resonance; gearbox; fault diagnosis

2015-07-13 责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2016.02.12

国家自然科学基金(51375319);河北省杰出青年科学基金(E2013210113);河北省百名优秀创新人才支持计划(BR2-222)

杨红娜(1989-), 女, 硕士研究生，主要从事机电系统故障诊断的研究。E-mail: yhn120130903@sina.com

TP277;TH17

A

2095-0373(2016)02-0061-06

杨红娜，郝如江.基于随机共振的齿轮箱早期故障诊断研究[J].石家庄铁道大学学报:自然科学版,2016,29(2):61-66.