基于近邻互信息的SVM-GARCH股票价格预测模型研究

张贵生，张信东

(1.山西大学管理与决策研究所，山西 太原 030006：2.山西大学经济与管理学院，山西 太原 030006)



基于近邻互信息的SVM-GARCH股票价格预测模型研究

张贵生1,2，张信东1,2

(1.山西大学管理与决策研究所，山西 太原 030006：2.山西大学经济与管理学院，山西 太原 030006)

为了克服传统线性模型分析处理收益率数据非线性因素的不足，本文提出一种新的基于近邻互信息特征选择的SVM-GARCH预测模型。该模型利用SVM处理高维非线性数据的优势，不仅包含了股指序列自身的历史数据信息，而且通过近邻互信息的方式融合了与目标股指数据关系密切的周边证券市场的相关变化信息。仿真实验结果表明，该模型在时序数据除噪、趋势判别以及预测的精确度等方面均优于传统的ARMA-GARCH模型。

股票价格预测：SVM-GARCH模型；近邻互信息

1 引言

随着人们对金融市场认识的不断加深，国内外广大研究人员提出了大量的金融时序数据的分析预测模型，在这些方法中有基于传统统计理论的ARMA模型[1-2]、GARCH模型[3-4]及马尔科夫链[5-6]等，也有人工神经网络算法(Artificial Neural Network，ANN)[7-8]、支持向量机(Support Vector Machine，SVM)[9-10]等基于机器学习的人工智能方法。在这许多方法之中，ARMA-GARCH模型在对因变量滞后值以及随机误差项的滞后值进行回归的基础之上，还对误差方差和滞后条件方差进行了进一步的线性函数建模，在对于金融时序数据的收益和波动性等研究方面得到了广泛地应用[11-16]。然而，股票价格的影响因素很多，而且随着全球经济金融市场的一体化发展以及金融危机的爆发，各国证券市场之间的相互影响正日益扩大，不同金融市场之间的联动和传染效应也对股票价格有着非常显著的影响，已经成为影响本地证券市场波动的主要因素之一[17]，所有这些因素使得股票价格的波动表现出复杂的非线性特征和不确定性[18-22]。而ARMA方程是一种典型的线性回归模型，对于证券价格线性趋势变化的假设，影响了在现实应用中预测精度的进一步提高[23-28]。近年来，借助机器学习和智能计算技术克服传统规范分析研究假设过于严格的弱点[29-30]，创新性地把ANN和SVM等非线性算法大量应用于股票价格预测研究，很大程度上提高了股票价格预测的精度。但神经网络由于存在诸如网络结构复杂、过拟合、局部极小值等缺陷，影响了在证券价格预测研究中的性能[25，31-32]。而支持向量机基于结构风险最小化原则克服了神经网络的缺陷，已经在经济、金融研究领域得到了广泛地应用[33-36]。利用SVM模型通过高维面板数据可以更好地分析处理金融时序数据中的非线性成分，但并不能确保回归后的扰动项不存在异方差性。基于以上思路本文拟构造一种SVM-GARCH模型，利用SVM分析收益率时间序列中非线性复杂关系的同时，通过GARCH模型处理预测残差的异方差特性，进一步在一定程度上解决SVM对于预测目标相关信息学习不完备的问题。另外，本文借用近邻互信息的概念刻画不同金融市场之间的非线性依赖关系的基础上进行SVM输入变量的特征选择，提高SVM模型对于收益率时序数据非线性关系的分析和预测能力。最后，以多期日经225指数为实验对象的实验结果表明，学习了周边证券市场联动信息的SVM-GARCH模型更加贴近真实的证券市场环境，预测的有效性和精确性有显著提高。

2 SVM-GARCH模型构造

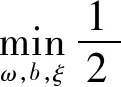
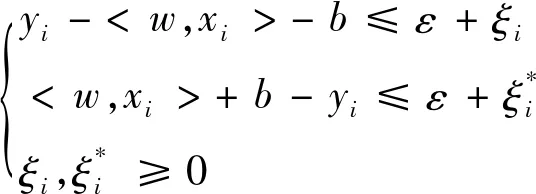
(1)

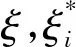
(2)

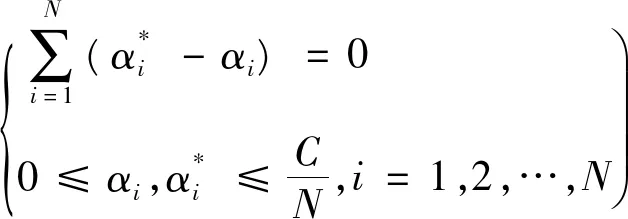
我们能得到当输入为x时的预测结果f(x)：

(3)

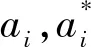
定义1.假设rt为收益率时间序列数据，则SVM-GARCH模型的均值方程和方差方程如下：

(4)

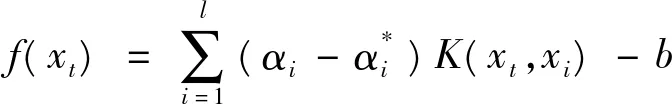
在金融市场联动研究方面，当前普遍采用的GARCH、VAR、协整以及误差修正等计量经济学模型样本需要事先假设残差的条件分布，不能很好地适应金融时序数据的真实特性，在一定程度上影响了模型对于市场联动信息分析判断的准确性[18]。鉴于此，本文采用近邻互信息的方法，从微观层面描述不同市场之间的联动规律。由于近邻互信息是在信息熵的基础之上演化而来，因此不仅客服了离散数据之间互信息的计算困难，而且还满足了金融市场之间非线性相互关系的要求，因此本文选择近邻互信息来刻画周边市场与目标市场收益率数据之间的相关性，并以近邻互信息最大化原则对自身收益率历史数据及关联市场收益率历史数据进行特征选择[39-40]。近邻互信息定义如下[41]：

定义2.若样本集U={x1，x2，…，xn}由离散的数值特征集F描述，R，S为特征集F的特征子集，即R，S⊆F，样本xi在特征子集R和S上的近邻域可分别表示为δR(xi)和δS(xi)，则R与S的近邻互信息定义为：

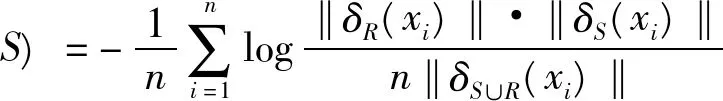
(5)

本文构建的基于近邻互信息特征选择的SVM-GARCH股票价格收益率时间序列的预测模型的总体思路为：首先使用近邻互信息选择与目标市场收益率关联性较强的目标市场历史数据及周边市场信息，构造支持向量回归机的高维输入变量信息；然后训练SVM分析处理收益率时间序列数据；最后使用GARCH模型分析残差序列异方差特性，矫正并改善SVM-GARCH模型预测的有效性和精确性。基于互信息的SVM-GARCH预测模型算法描述见表1。

3 实证研究

由于本文是针对传统ARMA-GARCH模型在处理时序数据非线性结构时的不足提出的改进算法，因此在本文接下来的实证研究中将以证券市场中的真实股票价格时间序列数据为研究对象，以ARMA-GARCH模型为基准模型，通过比较研究证明SVM-GARCH模型的科学性，以及近邻互信息在表达当今复杂经济金融市场环境下的市场联动信息方面的适用性。

3.1 数据来源及预处理

日经225(Nikkei 225)股票指数由日本经济新闻社编制并由日本东京股票交易所推出，被认为不仅是最能够代表日本股票市场的股票价格平均指数，更是全世界国际金融市场中的重要指标之一。另一方面日本作为经济发达国家之一，在高外汇储备、 高储蓄、 高净出口等方面与中国有很多相似之处，作为亚太地区最成熟的股票市场是如何发挥其宏观经济的晴雨表作用的，对于当下全球经济金融一体化环境下的国内股票市场而言，在维护金融安全，推动经济发展等方面具有很大的参考价值[22,42]。基于对以上因素的综合考虑， 本文选取了2010年1月4日至2011年12月31日和2012年1月4日至2013年12月31日两段时间范围内的日经225指数日收益数据为实验对象，对基准模型ARMA-GARCH和新模型SVM-GARCH展开实证比较研究，检验模型预测结果的精确性。两部分数据集的前90%作为训练数据集，主要训练模型的学习能力并对相关参数进行估计，剩余10%作为测试集，用于样本外测试，检验模型的学习效果和预测精度。本文中仿真实验所涉及股指数据全部来自Datastream金融数据库。设股指日收盘价格为Ci，则每日收益率为ri=(Ci-Gi-1)/Ci-1，本文研究过程中，使用股指日收益率数据为建模对象展开实证研究。SVM回归机由Weka3.6.11工具箱实现，近邻互信息数值计算代码由VisiualStudio2013语言环境自主开发完成，模型构建中GARCH模型通过MATLAB2014b工具箱以及EVIEWS8.0完成。

3.2 模型参数选择

从表2中给出的两段日经225综合指数收益序列的相关统计量信息可以看出，收益率时间序列的峰度值分别为10.30446和5.72311 1均大于正态分布的峰度值3，表中J-B统计量检验结果也表明收益率序列服从正态分布的概率为0，并且偏度值也都小于0，说明两段日经225股指收益率序列均具有尖峰左偏的分布特点。表3给出了两段收益率时间序列的ADF单位根检验结果，在1%显著水平下，ADF统计量分别为-20.75900和-22.61832均远小于临界值且P值很小，说明收益率序列有单位根的概率几乎为0，应该没有明显的记忆性和波动的持续性，文中所选取的两段日经225股指收益率时间序列是平稳的。

表1 基于近邻互信息的SVM.GARCH单步预测模型算法

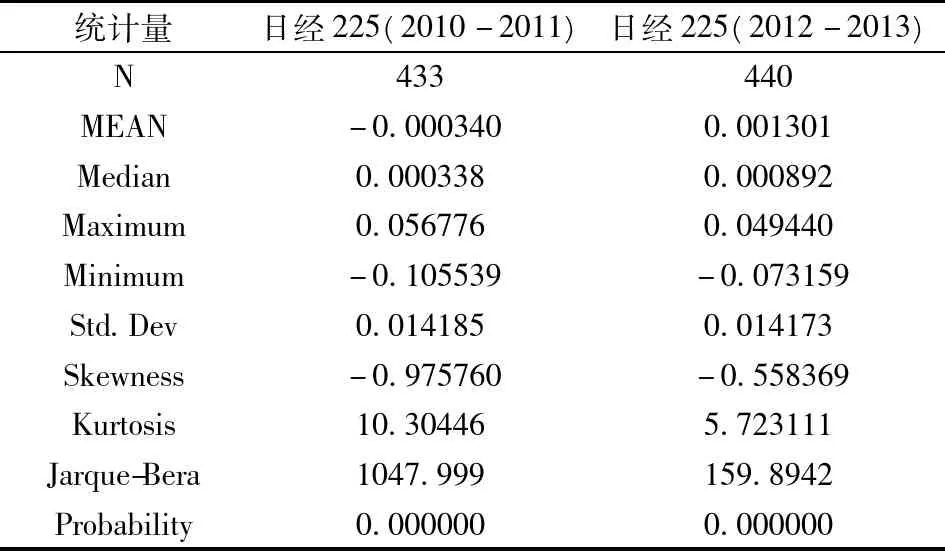
表2 收益序列ri统计特征

表3 收益率序列的ADF检验结果

在确定ARMA模型的具体形式时，通常情况下以计算AC和PAC并通过图像来直观地进行滞后阶数p，q可能取值的判断，然后通常采用最小信息准则(AIC)给出最佳的模型阶数定量化的精确判断。其中，AIC函数的具体定义为：

(6)

根据AIC最小准则，对于两阶段日经225指数收益率数据我们分别选择p=2、q=2和p=2、q=3，即2010-2011段数据确定ARMA(2，2)模型，而对于2012-2013段数据选取ARMA(2，3)模型。

大量研究表明，互信息在构建模型进行特征选择时是一种有效的方法。并且Hu Qinghua等[41]在2011年提出的近邻互信息概念不仅满足了表达收益率时间序列之间非线性关系的需求，而且解决了传统互信息在计算数值型离散数据的互信息时计算相关边缘概率密度及联合概率密度的困难。因此在本文中利用近邻互信息的概念实现SVM的高维输入变量的特征选择功能。考虑到日经225指数在全球证券市场的广泛影响力和在亚洲的特殊地位，本文在开展实证研究时选取了欧洲三大股指(英国富时100、德国法兰克福指数和法国CAC40股价指数)，纽约三大股指(道琼斯指数、标准普尔500指数和纳斯达克指数)、香港恒生指数以及我国内地的上证综指和深成指数的滞后5天历史数据作为基础数据，并分别计算以上信息与日经225指数之间的近邻互信息，计算所得结果如表4所示。

表4 互信息计算结果

从表4中对于两组数据的计算结果可以看出，与日经225指数近邻互信息由强到弱的前20个数据集信息依次为日经225指数滞后5天历史数据信息、道琼斯指数、法兰克福指数和香港恒生指数。作为亚洲最成熟证券市场中的代表性综合指数，日经225指数不仅与美欧发达国家的综合性股指数据关联密切而且也和香港恒生指数有着很强的联动效应，体现了市场较高的成熟度和开放程度。本文分别选取了表4中的前10个和前20个属性作为SVM的高维输入变量，构建日经225指数的预测模型SVM(10)-GARCH和SVM(20)-GARCH，并得到相应的预测结果。

文中对ARMA、SVM(10)和SVM(20)对于收益率预测结果的残差序列进行了滞后5期的ARCH-LM检验。从表5可看出，检验统计量LM=TR2和对应的概率几乎全部为0，统计结果拒绝了残差序列中不存在异方差性的原假设，即两组日经225股指收益率序列在经过不同的线性和非线性回归后的残差项中均存在明显的异方差效应。因此在构建ARMA模型和SVM模型时，需要加入GARCH模型对其回归预测结果的残差平方进行进一步的分析处理，同时估计两组时间序列数据集的ARMA-GARCH模型和SVM-GARCH模型的相关参数，结果如表6所示。将表中的参数估计结果代入ARMA-GARCH方程和SVM-GARCH方程，可分别得到对应的线性模型和非线性模型的条件均值方程和方差方程。本文以日经225指数2010-2011段数据为例将上述得到的参数估计结果代入不同的预测模型，分别得到股指日收益率序列数据的ARMA-GARCH，SVM(10)-GARCH及SVM(20)-GARCH的条件均值方程及条件方差方程，具体情况如式(7)-(12)所示。

日经225指数ARMA(2，3)-GARCH(1，1)模型的条件均值方程和方差方程分别为：

yt=0.0011-0.5872yt-1-0.8319yt-2+0.6031ut-1+0.8804ut-2+0.1058ut-3

(7)

(8)

SVM(10)-GARCH(1，1)模型的条件均值方程和方差方程分别为：

yt=1.9607×10-4+0.7279f(x)- 0.0321ut-1-0.0262ut-2+0.0315ut-3

(9)

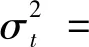
(10)

SVM(20)-GARCH(1，1)模型的条件均值方程和方差方程分别为：

yt=3.1487×10-4+0.9362f(X)-0.0484ut-1—0.0047ut-2+0.0258ut-3

(11)

(12)

表6中列出的参数在95%置信水平下均是高度显著的。两组数据的ARMA方程中p值均为2，g的取值分别为2和3，说明受各种综合因素的影响，市场交易行为对于历史数据信息的理解一般需要两到三天的时间。SVM方程的系数相对较大，说明了SVM在分析高维非线性的面板时序数据时的适用性，也体现了其在新的SVM-GARCH模型中的重要性。到此对于两阶段日经225指数时序数据测试集的ARMA-GARCH方程和SVM-GARCH方程均已经建立完毕。并且本文又对得到的模型分别作了1阶滞后，10阶滞后和20阶滞后的残差估计，验证模型已不存在异方差性，因此可以认为模型的构建是完全合理的。

3.3 实验结果分析

为了检验模型的预测准确性， 本文以两组日经225指数的日收益率时间序列的10%作为测试集，展开对于ARMA-GARCH模型和两种不同的特征选择后的SVM-GARCH模型的实证比较研究，图1至图4分别显示了预测模型在不同测试数据集上预测结果的时序图和散点图。从一系列时序图中可以看出，两种模型的预测结果均较好地拟合了收益序列的真实值，但SVM-GARCH模型对于不同测试数据集的预测结果在数据变化趋势及波动幅度方面均更加贴近真实收益率数值的变化情况。说明SVM-GARCH模型能更好地分析处理收益率时间序列数据中所包含的非线性因素，而且也证实了当前全球经济一体化环境下的周边金融市场信息对于目标市场收益变动日益显著的影响作用。另外，从不同模型预测结果的散点图也可以清晰地看出，SVM-GARCH模型的预测结果更加接近R2=1的最佳回归线，而ARMA-GARC模型的预测结果则分布得更加分散。以图1(b)的散点图为例，SVM(10)-GARCH模型对于真实收益率数据中的方差解释能力由ARMA-GARC模型的0.7415提高到了0.8696，表明SVM-GARCH模型显著地改善了预测模型对于时序数据的分析和预测能力。

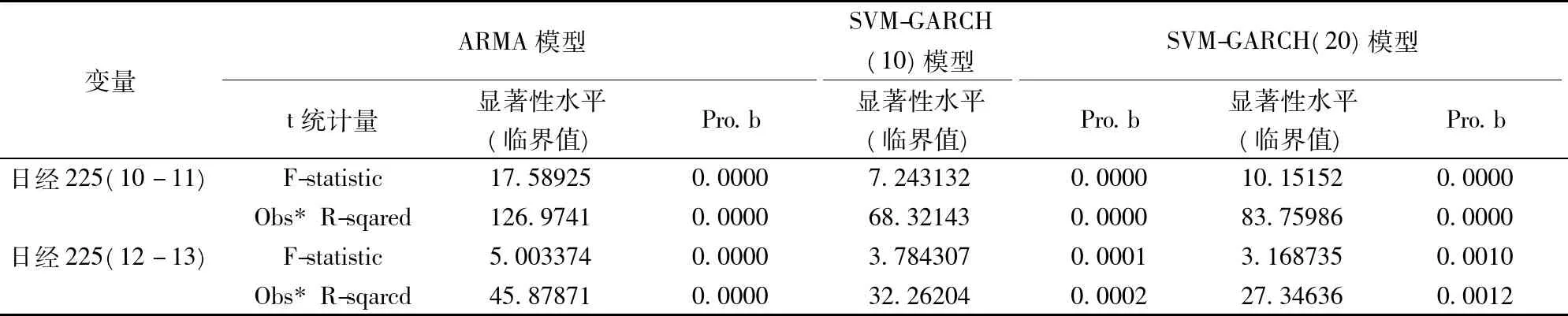
考虑到评价标准在实际应用领域中的特点和局限性，任何一个单个或单方面的评价指标都很难做到对于计算结果优劣的综合全面评价。根据Hansen等[43]的建议，考虑到评价的全面性和客观性，文中选取了平均绝对误差(Mean Absolute Error，MAE)，均方根误差(Root Mean Square Error，RMSE)，平均绝对百分误差(Mean Absolute Percent Error，MAPE)，百分标准差(Percent Standard error of Prediction，SEP)，Nash-Sutcliffe系数(Nash Sutcliffe Efficiency Coefficient，E)，一致性指数(Willmott’s Index of Agreement，WIA)，方向准确率(Direction Accuracy，DA)等一系列标准，旨在从多方面对于不同模型的泛化能力做出全面而又客观的科学评价。评价标准具体定义如下：

(13)

(14)

表6 模型参数估计结果

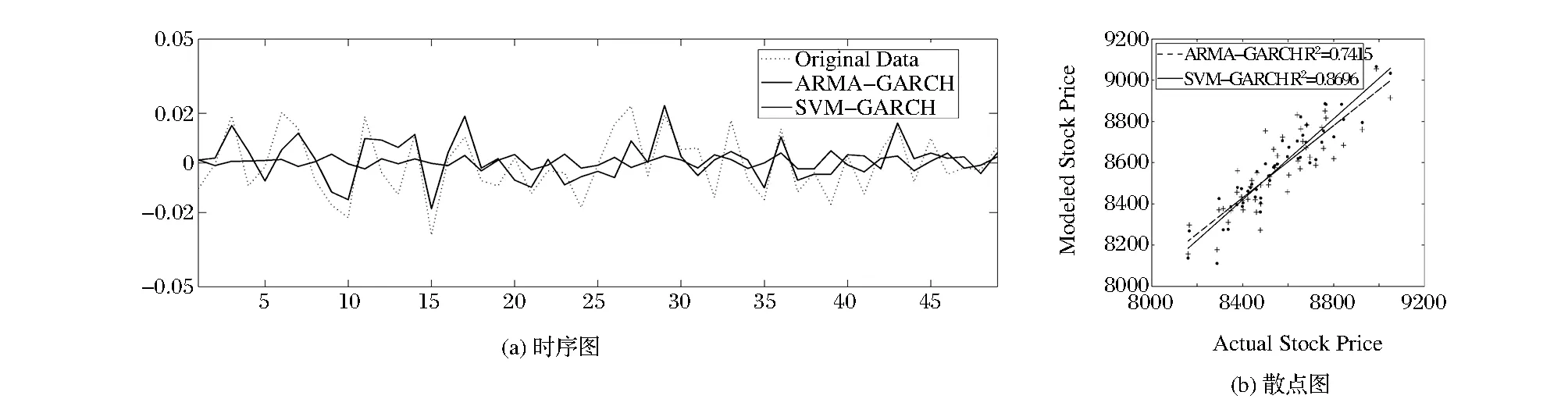
图1 2010-2011段日收益率数据SVM(10)-GARCH模型预测结果

图2 2010-2011段日收益率数据SVM(20)-GARCH模型预测结果

图3 2012-2013段日收益率数据SVM(10)-GARCH模型预测结果

图4 2012-2013段日收益率数据SVM(20)-GARCH模型预测结果

(15)

(16)

(17)

(18)

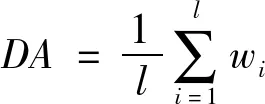
(19)

其中ai和yi分别表示真实值和模型的预测值。通常，评价指标MAE，RMSE，SEP以及MAPE的值越小表明模型的预测值与真实值更加接近，也就说明模型预测精度更高。E表示模型的预测能力，当预测值与真实值完全相等时E取最大值1，而IA以及DA反映了模型预测结果与真实值的一致程度以及对于未来时序数据变化趋势的判别能力，E、IA和DA的值越大，则表明模型的预测能力越强、精度越高。

表7列出了ARMA-GARCH模型以及SVM(10)-GARCH模型和SVM(20)-GARCH模型在不同股指数据测试集上预测结果的多角度评价情况。从表中各种评价指标的数据可以直观地看出，经过特征选择的SVM-GARCH模型均表现出了更加优异的性能。以2010-2011数据段为例可看出，预测结果的MAE值从ARMA-GARCH模型的85.99153分别下降为SVM(10)-GARCH模型的63.74392和SVM(20)-GARCH模型的59.20412，降低比例超过了25%，其它指标RMSE，MAPE，SEP等也有显著的改善，说明SVM-GARCH模型预测性能提高显著。另外，由于SVM-GARCH模型在均值方程中用SVM替代了线性自回归，改善了模型对于时序数据高维非线性成分的分析和处理能力，并通过融合周边市场信息的方式更加全面地表达了全球经济一体化环境下影响股票价格时序数据收益和波动的复杂性综合因素，使得SVM-GARCH模型对于不同的测试集在一致性(WIA)尤其是在对于预测结果更为重要的方向性判别(DA)方面均体现了一致趋优的良好性能。结果再次说明通过近邻互信息对周边市场收益数据的筛选，不仅有效利用了SVM处理高维数据的特性，而且还科学地表达了新的经济环境下，周边市场信息对于目标金融市场走势及波动的影响，能更准确地把握股票市场价格行为的变化规律，很大程度上弥补了传统ARMA-GARCH模型仅仅分析单变量股票价格历史数据信息不够全面的缺陷，提高了模型预测的准确性和鲁棒性。

表7 评价指标结果

4 结语

影响股票市场的因素很多，而且随着全球经济一体化趋势的不断加强，不同区域金融市场之间的联动关系和传染效应表现得越来越显著，进一步增强了股指收益率时序数据的高维复杂性特征。因此通过构建模型对未来股票收益率时间序列进行预测时，不能只关注于单变量时序数据本身所包含的有限信息，而是要赋予市场主体一些特定的行为模式及学习机制，并强调真实的开放市场环境下所有参与对象之间的微观交互，充分挖掘与目标股指数据关系密切的周边证券市场的相关变化信息，进而增强模型对于宏观市场运行规律的学习能力。基于此，本文提出了一种基于近邻互信息特征选择的SVM-GARCH预测模型，新的模型充分利用SVM处理高维面板数据的优势，在考虑股指收益率自身历史数据信息的基础上，还借助近邻互信息技术科学有效地融合了真实市场环境下影响目标市场收益率的周边金融市场变化信息。该模型不仅改进了传统线性仿真模型的设计，增强了模型分析收益率时间序列数据非线性复杂结构的能力，还通过与GARCH模型结合克服了SVM模型处理预测结果残差序列中异方差效应的不足，使得模型更加贴近了真实的市场环境。对于不同阶段日经225指数日收益率数据的数值仿真实验表明，基于近邻互信息特征选择的SVM-GARCH模型更加充分地表达了影响股指收益率波动的综合市场因素，在对于时序数据未来变化趋势判别、数据除噪以及预测精确度等多方面均优于传统的ARMA-GARCH模型。该方法进一步丰富了计算实验金融研究领域中关于金融时序数据分析预测的方法和措施，对于金融市场风险预警体系的完善以及投资决策的辅助设计均有一定的借鉴意义。

将非线性技术与现代金融理论相结合，是当前金融理论研究的热点之一。本文紧跟这一热点，对金融时序数据的预测性研究做了一些有益的探索。旨在从数据驱动的角度出发，融合金融时序数据内在特点的基础上增强预测模型对于时序数据的解读能力，进而提高模型的预测精度。但是在金融市场发生大规模突发性事件的环境下，金融时序数据震荡或反转突变情况会大幅增加时，金融时序历史数据的相关信息对于模型预测精度提高的指导意义就会大打折扣，以数据信息驱动的预测模型的适应性就会收到一定程度的影响。我们希望在未来的后续研究工作中继续深入分析特殊市场环境下的时序数据形态和特征，使得模型能够满足特殊事件驱动的时序数据预测精度要求，为投资策略选择及市场金融监管提供有效的决策辅助信息。

[1] Wang Jujie，Wang Jianzhou，Zhang Z，et al. Stock index forecasting based on a hybrid model[J].Omega，2012，40(6)：758-766.

[2] Pal Pingfeng，Lin C.A hybrid ARIMA and support vector machines model in stock price forecasting[J].Omega,2005，33(6)：497-505.

[3] 曹广喜，曹杰，徐龙炳.双长记忆GARCH族模型的预测能力比较研究-基于沪深股市数据的实证分析[J].中国管理科学，2012，20(2)：41-49.

[4] 张锐，魏宇，金炜东.基于MRS-EGARCH模型的沪深300指数波动预测[J].系统工程学报，2011，26(5)：628-635.

[5] 姜婷，周孝华，董耀武.基于Markov机制转换模型的我国股市周期波动状态研究[J].系统工程理论与实践，2013，33(8)：1934-1939.

[6] 杨继平，张春会.基于马尔可夫状态转换模型的沪深股市波动率的估计[J].中国管理科学，2013，21(2)：42-49.

[7] 于志军，杨善林，章政，等. 基于误差校正的灰色神经网络股票收益率预测[J].中国管理科学，2015，23(12)：20-26.

[8] 王文波，费浦生，羿旭明.基于EMD和神经网络的中国股票市场预测[J].系统工程理论与实践，2010，30(6)：1028-1033.

[9] Kim K. Financial time series forecasting using support vector machines[J].Neurocomputing，2003，55(1-2)：307-319.

[10] Huang Wei，Nakamori Y，Wang Shouyang.Forecasting stock market movement direction with support vector machine[J].Computers & Operations Research，2005，32(10)：2513-2522.

[11] Engle R F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J]. Econometrica，1982，50(4)：987-1007.

[12] Bollerslev T.Generalized autoregressive condi-tional heteroskedasticity[J].Journal of Econometrics，1986，3 1(3)：307-327.

[13] 侯利强，杨善林，王晓佳，等.上证综指的股指波动：基于模糊FEGARCH模型及不同分布假设的预测研究[J].中国管理科学，2015，23(6)：32-40.

[14] Mohammadi H， Su Lixian.International evidence on crude oil price dynamics：Applications of ARIMA-GARCH models[J].Energy Economics，2010，32(5)：1001-1008.

[15] Liu Heping， Shi Jing.Applying ARMA-GARCH approaches to forecasting short-term electricity prices[J].Energy Economics，2013，37：152-166.

[16] 吴恒煜，朱福敏，温金明.基于ARMA-GARCH调和稳态Levy过程的期权定价[J].系统工程理论与实践，2013，33(11)：2721-2733.

[17] 周璞，李自然.基于非线性Granger因果检验中国大陆和世界其他主要股票市场之间的信息溢出[J].系统工程理论与实践，2012，32(3)：466-475.

[18] 沈传河，王向荣.金融市场联动形态结构的非线性分析[J].管理科学学报，2015，18(2)：66-75.

[19] Loh L.Co-movement of Asla-Pacific with European and US stock market returns：A cross-time-frequency analysis[J].Research in International Business and Finance，2013，29：1-13.

[20] Kotkatvuori-Örnberg J,Nikkinen J,ijö J.Stock market correlations during the financial crisis of 2008-2009：Evidence from 50 equity markets[J].International Revlew of Financial Analysis，2013，28：70-78.

[21] 黄飞雪，谷静，李延喜，等.金融危机前后的全球主要股指联动与动态稳定性比较[J].系统工程理论与实践，2010，30(10)：1729-1740.

[22] 林宇. 中国股市与国际股市的极值风险传导效应研究[J].中国管理科学，2008，16(4)：36-43.

[23] Xiong Tao，Li Chongguang，Bao Yukun，et al．A combination method for interval forecasting of agricultural commodity futures prices[J].Knowledge-Based Systems,2015，77：92-102.

[24] Zhang G P．Time series forecasting using a hybrid ARIMA and neural network model[J].Neurocomputing，2003，50：159-175.

[25] Zhu Bangzhu，Wei Yiming.Carbon price forecasting with a novel hybrid ARIMA and least squares support vector machines methodology[J].Omega, 2013，41(3)：517-524.

[26] 陈海英. 基于支持向量机的上证指数预测和分析[J].计算机仿真，2013，30(1)：297-300.

[27] 张贵生，张信东.基于时间相关性的股票价格混合预测模型[J].经济问题，2015，(9)：23-28.

[28] 于志军，杨善林.基于误差校正GARCH的股票价格预测模型[J].中国管理科学，2013，21(S1)：341-345.

[29] 张维，赵帅特，熊熊，等.计算实验金融、技术规则与时间序列收益可预测性[J].管理科学，2008，21(3)：74-84.

[30] 张维，李悦雷，熊熊，等.计算实验金融的思想基础及研究范式[J].系统工程理论与实践，2012，32(3)：495-507.

[31] Cao Lijuan. Support vector machines experts for time series forecasting[J].Neurocomputing,2003，51：321-339.

[32] 谢国强.基于支持向量回归机的股票价格预测[J].计算机仿真，2012，29(4)：379-382.

[33] Vapnik V．The nature of statistical learning theory[M].1995，New York:Springer Verlag Press.

[34] Atsalakis G S．Valavanis K P．Surveying stock market forecasting techniques-Part II：Soft computing methods[J].Expert Systems with Applications,2009，36(3)：5932-5941.

[35] 熊涛，鲍玉昆，胡忠义，张金隆.基于SOM和SVMs的沪深300指数多步预测[J]．系统工程，2012，30(10)：36-42.

[36] 李海燕.基于支持向量机算法的股市拐点预测分析[J].郑州大学学报(哲学社会科学版)，2015，48(1)：96-99.

[37] 苏治，傅晓媛.核主成分遗传算法与SVR选股模型改进[J].统计研究，2013，30(5)：54-62.

[38] 王晴.组合模型在股票价格预测中应用研究[J].计算机仿真，2010，27(12)：361-364.

[39] Hossein H，Andreia D，Mansoureh G．Effct of noise reduction in measuring the linear and nonlinear dependency of financial maricets[J].Nonlinear Analysis：Real World Applications，2010，11(1)：492-502.

[40] Dionisio A,Menezes R,Mendes D A．Mutual information：A measure of dependency for nonlinear time series[J].Physica A，2004，344(1-2)：326-329.

[41] Hu Qinghua，Zhang Lei，Zhang D，et al．Measuring relevance between discrete and continuous features based on neighborhood mutual information[J]．Expert Systems with Applications，2011，38(9)：10737-10750.

[42] 章宇轩.基于ARMA模型的日经225指数实证研究[J].中国外资，2013(8):174-175.

[43] Hansen P R，Lunde A．A forecast comparison of volatility models：Does anything beat a GARCH(1，1)[J].Journal of Applied Econometrics，2005，20(7)：873-899.

A SVM-GARCH Model for Stock Price Forecasting Based on Neighborhood Mutual Information

ZHANG Gui-sheng1,2, ZHANG Xin-dong1,2

(1.Institute of Management and Decision, Shanxi University, Taiyuan 030006, China;2.School of Economics and Management, Shanxi University, Taiyuan 030006,China)

In order to overcome the limitations of the traditional linear model in dealing with the nonlinearity in time series, a novel SVM-GARCH forecasting model is proposed based on the neighborhood mutual information. By constructing high dimensional input variables, the proposed nonlinear model not only absorbs the historical information in the time series data but also incorporates the stock market information in different regions through feature selection by the neighborhood mutual information. Empirical studies demonstrate that the proposed model is superior to the traditional linear ARMA-GARCH model in terms of data denosing, trend discrimination and prediction accuracy etc.

stock price forecasting; SVM-GARCH model; neighborhood mutual information

2015-11-09；

2016-03-24

国家自然科学基金面上项目(71371113)；教育部人文社会科学研究项目(13YJA790154)

简介：张贵生(1977-)，男(汉族)，山西晋中人，山西大学经济与管理学院，讲师，博士，研究方向：金融资产价格预测性研究、预测支持系统,E-mail:zhanggs@sxu.edu.cn.

F224.12

A

1003-207(2016)09-0011-10

10.16381/j.cnki.issn1003-207x.2016.09.002