基于CAViaR模型的沪深300股指期货隔夜风险研究

简志宏，曾裕峰，刘曦腾

(1.华中科技大学经济学院，湖北 武汉 430074；2.复旦大学经济学院，上海 200433； 3.上海财经大学公共经济与管理学院，上海 200433)



基于CAViaR模型的沪深300股指期货隔夜风险研究

简志宏1，曾裕峰2，刘曦腾3

(1.华中科技大学经济学院，湖北 武汉 430074；2.复旦大学经济学院，上海 200433； 3.上海财经大学公共经济与管理学院，上海 200433)

期货隔夜风险的防范历来是投资者关注的热点，本文以沪深300股指期货为研究对象，采用CAViaR模型对普通隔夜风险进行度量，同时还采用新建的CAViaR-EVT模型对极端隔夜风险进行预测，全面地分析了多头VaR和空头VaR在不同分位数的动态变化特征，最后采用Kupiec似然比检验和动态分位数检验对模型进行后测检验。实证结果表明，隔夜收益序列具有右偏、无长期记忆性和尖峰厚尾等典型特征；CAViaR模型对股指期货的普通隔夜风险具有优异的预测能力，其中AS模型的预测效果最好；加入极值理论后，CAViaR-EVT模型同样能很好地刻画极端分位数下隔夜风险的动态演化过程，且其预测结果比EVT和GARCH-EVT模型要更合理。

隔夜风险；CAViaR模型；沪深300股指期货；VaR

1 引言

2010年4月16日我国正式推出沪深300股指期货，填补了我国金融期货的空白。经过五年的孕育成长，目前已成为我国交易量最大的期货品种。由于我国股指期货市场还没有采用连续交易机制，因而可分为交易时间和休市时间。在交易时间内投资者可以自由地进行竞价买卖，但是白天交易结束后，投资者当天买入的头寸在第二天开盘前处于敞口状态，而恰恰此期间是上市公司信息公告发布的密集区[1],如果新信息进入市场，那么它对价格的累计影响将会直接反映到第二天的开盘价，从而使得股指期货的开盘价出现“跳空上涨”或“跳空下跌”。本文将投资者持有的头寸在当天休市前未能及时平仓，从而给投资者带来隔夜损益的不确定性称为隔夜风险。在实务界,市场参与者都将其视为不确定性的大源头(特别是在我国期货市场)，期货是一种高杠杆化的金融衍生产品，随着期货价格对于信息反映的时滞越来越短，加之当前国际金融市场不稳定因素越来越多，因此,一旦休市期间期货市场遭遇到不利的外部冲击，投资者持有的头寸会在开盘瞬间发生跳跃性变动，从而会给投资者带来巨大风险，甚至出现爆仓的可能性。所以，无论是对股指期货市场的各类投资者还是我国的金融监管当局而言, 对股指期货隔夜风险的波动特征和风险状况进行准确的刻画和科学的预测, 进而探索有效的期指市场风险防范和监控手段, 都具有非常重要的现实意义。

在理论界，由于交易数据的限制和相关理论的不成熟，使得隔夜信息一直没有得到足够的重视。直到Andersen和Bollerslev[2]首次提出用高频数据的日内收益率平方和来估算已实现波动率。众多学者才开始关注隔夜波动率，并将隔夜波动率视为日内已实现波动率的延续，两者之和才构成日已实现波动的最优测度[3-4]。Taylor[5]利用条件波动的线性回归模型评价了1998-2002年S&P500期货市场隔夜交易的预测能力，并论证了含隔夜信息模型的波动预测能够带来更准确的风险价值测度。Andersen等[6]认为隔夜收益是整日收益的重要组成部分，可将其看作是动态相依的跳跃时间序列，并基于GARCH-t模型对美国期货的高频数据分析，结果表明日内连续性波动对隔夜波动具有显著的对称解释能力，而日内跳跃性波动解释效果不显著。近几年国内已有学者开始关注隔夜信息，如刘庆富和张金清[7]基于随机波动模型检测了商品期货隔夜信息对日间交易的影响，实证结果发现总隔夜收益对日间收益及其波动均具有显著的预测能力。简志宏和李彩云[8]采用HAR-CJ-M模型对我国沪深300股指的隔夜收益波动率直接建模分析，结果发现大的隔夜波动率具有波动聚集性且可以被预测，但小的隔夜波动是市场微观噪声造成，不具备可预测性。上述国内外研究主要阐述了隔夜信息的重要性和隔夜波动率的可预测性，但是目前国内还没有以股指期货隔夜收益为直接研究对象，更没有将隔夜风险纳入到VaR理论体系内进行风险管理的文献。

Engle和Manganelli[9]创造性地直接对VaR进行自回归建模，提出了CAViaR(Conditional Autoregressive Value at Risk)模型，由于该方法不对收益分布做任何假设，并且对于具有尖峰厚尾、长记忆性和非对称性等典型事实的金融数据而言，该方法具有明显的优势，因此自提出以来在国内外得到了广泛的应用。Huang Dashan等[10]用改进的CAViaR模型考察了WTI现货石油收益对VaR的不对称的影响，并使用混合数据回归模型(Mixed Data Regression Model)预测了石油价格的多期VaR值。Huang Dashan等[11]基于模型系数与宏观经济变量联动性的事实，提出系数时变的指数兴奋CAViaR(Index-Exciting CAViaR)模型，实证结果表明该模型在市场之间存在溢出效应时表现最佳。闫昌荣[12]通过构造流动性调整的CAViaR模型，从而为投资者提供了一个流动性风险管理的有效途径。陈磊等[13]将AS-CAViaR模型的一阶自回归项进行门限分解，提出新的TCAViaR模型，更好地分析了石油期货左尾和右尾不同分位数下尾部风险影响因素的差异。同时，陈磊等[14]为避免传统CAViaR模型的估计风险和模型风险，构造出贝叶斯CAViaR模型，该模型显著地提高了布伦特原油油价的VaR预测绩效。可见CAViaR模型在相关的金融风险管理研究中已经得到了很好的运用，考虑到股指期货的隔夜收益是瞬时的收益序列，它不存在微观的交易信息，因此采用高频数据的VaR方法根本行不通，而且CAViaR模型避免了GARCH族模型求解波动率和残差分布等复杂的变量，因此为刻画隔夜风险的动态变化提供了独特的视角。

就目前已有的国内国外文献，实质意义上对隔夜风险进行研究的文献仅有一篇，即简志宏和李彩云[8]的研究。该文章用隔夜波动来度量隔夜风险，然而方差风险对高出均值的投资结果和低于均值的投资结果赋予相同的权重，难以符合实际，现实生活中投资人的效用函数中常对损失带来的负效用施以更大的权重，对收益带来的正效用给予较小权重，而本文采用VaR理论来度量隔夜风险；其次，该文是针对沪深300指数的隔夜风险进行分析，而本文是针对股指期货进行分析，实践意义可能更重大。总之，本文的研究角度和方法与之均不相同。为了更好地完善现有的文献，本文有以下几点贡献：首先，本文创新性地将股指期货的隔夜风险纳入到VaR风险管理的分析框架下，并尝试用CAViaR模型去度量沪深300股指期货隔夜风险；其次，将极值理论和CAViaR模型结合起来构造新的CAViaR-EVT模型，并对极端隔夜风险进行预测，有效地克服了现有模型的不足；最后，同时考虑了隔夜风险的左尾分位数和右尾分位数的变化特征，对具有买空卖空交易的期货市场而言，分析角度更加全面、现实意义更重大。

2 数据来源及描述性统计

本文选取的数据为沪深300股指期货市场2010年4月16日到2015年5月18日的实时交易数据。我国沪深300股指期货有当月、下月、下季和隔季四个期货合约，但当月连续的期货合约交易最活跃，因此本文选用当月连续合约的日度数据来构造连续收益序列，最后总共得到1232个有效的交易日数据，其中前732个数据作为样本内数据，最后500个数据作为样本外后测检验使用。数据均来源于Wind数据库。

目前我国沪深300股指期货市场还没有实行连续交易，所以整日收益率可分解为隔夜收益率和日内收益率两个部分，隔夜收益率通过当日开盘价与前一日收盘价的对数差分求解而来，为了更清晰的表述，具体如图1所示。

图1 日收益率的构成

通过对隔夜收益率的原始统计和描述性结果发现，隔夜收益率的均值为0.038，且隔夜收益为正的天数达到670天，开平盘(指当天的开盘价和昨日的收盘价相同，由原始数据计算得出)的天数为29天，这在一定程度上表明股指期货开盘总体趋向跳空上涨，隔夜收益最大值和最小值分别为4.486和-3.535，由于我国股指期货是采用10%的保证金比例交易，那么杠杆化后的隔夜收益变动将被进一步放大，这充分说明了股指期货潜在隔夜风险不容忽视且有研究的必要性。偏度系数和超额峰度系数均在1%水平下显著，说明隔夜收益序列具有右偏和“尖峰厚尾”的性质。J-B统计量和QQ图的结果显示隔夜收益率具有显著的非正态性质。Ljung-Box Q统计量和ADF单位根检验结果显示隔夜收益率是不具有长记忆的平稳序列。

表1 隔夜收益描述性统计

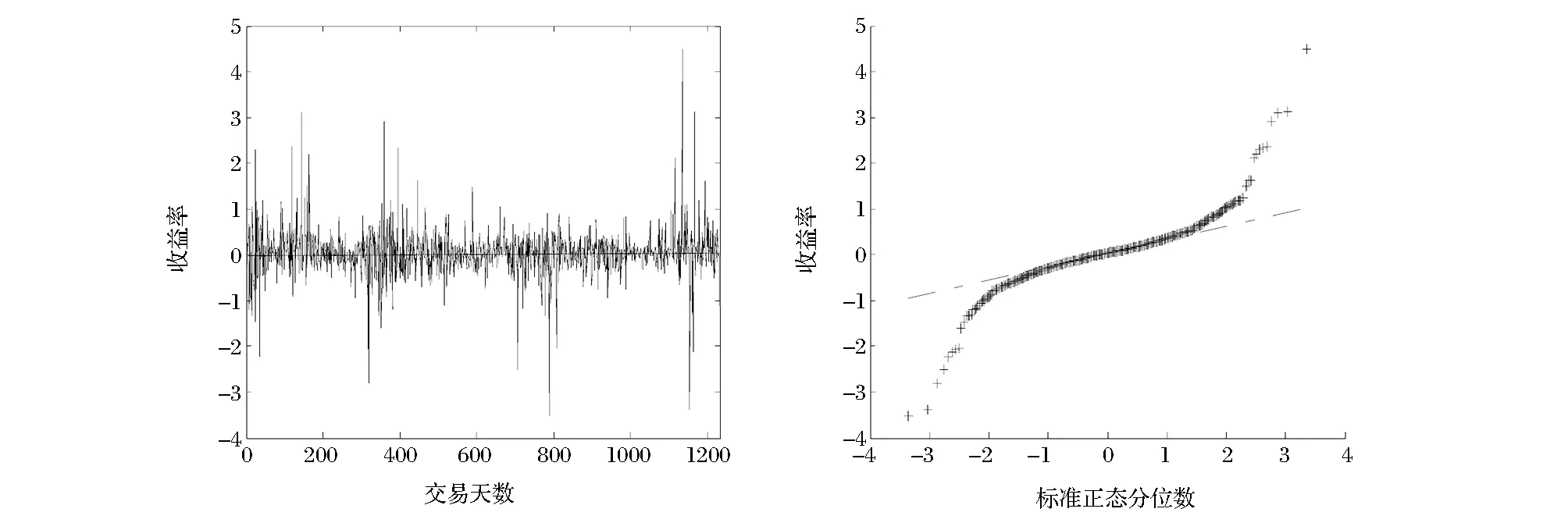
图2 沪深300股指期货隔夜收序列图和QQ图

另外，从图2明显可以看出，自沪深300股指期货上市至今主要有四个波动剧烈的区间：2010年4月份股指期货在刚推出时隔夜风险的波动较大，这可能是由于股指期货刚推出，市场上参与股指期货交易者以噪声交易者为主，投资主体不理性的交易行为导致隔夜波动较大；2011年8月份左右，股市大量资金出逃，出现严重的“钱荒”现象，A股市场疲软；2013年7月份左右，A股市场的增发配股、股权再融资和发债融资出现井喷之势，使得市场恐慌、投资者担忧再起，股市节节走低；2014年11月份开始，我国央行出台了宽松货币措施，市场投资者信心得到了提振，房市价格得到较好的控制，大量资金进入股市，使得整个股市的流动性非常充裕。

3 隔夜风险测度模型及估计结果

3.1 CAViaR模型

Engle和Manganelli[9]认为既然股票收益具有序列自相关性，而VaR的本质就是收益率序列的某一特定分位数，从而提出条件自回归风险价值模型(即CAViaR模型)对收益条件分位数直接建模。并给出了四种特殊形式的CAViaR模型，其中Adaptive模型在实证结果中表现最差，且被拒绝的概率最大。因此本文主要侧重于分析以下三个模型：

SAV-CAViaR模型：ft(β)=β1+β2ft-1(β)+β3|yt-1|

(1)

AS-CAViaR模型: ft(β)=β1+β2ft-1(β)+β3(yt-1)++β4(yt-1)-

(2)

(3)

其中，(yt-1)+和(yt-1)-分别表示滞后一期收益率的正部和负部，ft(β)表示收益率的条件分位数。方程(1)和(3)假设过去正负收益对未来风险的影响是对称的，AS-CAViaR模型本质上是SAV-CAViaR模型的一般形式，它反映了正负收益率对未来风险的非对称效应。

3.2 模型的估计结果

上述SAV-CAViaR模型、AS-CAViaR模型和IGARCH模型的估计均需要使用分位数回归(Quantile Regression)，分位数回归的思想最早由Koenker和Bassett[15]提出，它是最小绝对离差(Least Absolute Deviation，LAD)模型的特殊情形。Engle和Manganelli[9]采用Nelder-Mead simplex和quasi-Newton最优化算法估计上述模型参数，具体要优化的目标函数为：

(4)

其中，θ表示回归的样本分位数。相比均值回归，它能充分刻画自变量X对于因变量Y分布的位置、刻度和形状的影响。在残差序列服从高斯分布的情况下，分位数回归的估计效率只有很小的损失；针对不服从正态分布的时间序列，特别是对具有“尖峰厚尾”性质的金融收益序列，它能准确地捕捉到分布的尾部特征，因而使得分位数回归系数估计比普通最小二乘法具有更强的稳健性。

由于在我国股票市场卖空交易受到诸多限制，因此在相关的文献中一般选择左尾分位数(如1%和5%)来对未来风险进行VaR预测，但在沪深300股指期货市场中有多头和空头之分，期货价格上涨和下跌都会给相关头寸持有者造成损失，因此本文将两者结合起来共同分析，其中1%、5%和10%水平的分位数可以作为股指期货多头持有者所面临的风险，简称为多头风险；而99%、90%和95%分位数可以表示股指期货空头头寸持有者面临的风险，简称为空头风险。

在模型的参数估计中，取收益序列前300个观测值的θ经验分位数来初试化f1(β)。RQ值为目标优化函数(4)估计值。样本内DQ统计量主要是用来检验模型对样本内数据的拟合程度，当样本内DQ统计量的P值小于显著性水平0.05时，则拒绝该模型；反之，则接受该模型。样本内DQ统计量和

下文样本外DQ统计量有一定的差异性，具体解释可见Engle和Manganelli[9]。

由表2和表3可得出以下结论，第一，从样本内DQ检验结果来看，右尾所有模型都通过了DQ检验，而左尾只有AS模型全通过了DQ检验，说明CAViaR模型对刻画隔夜风险的右尾更具有优势，另外，AS模型又要比SAV模型和IGARCH模型更优异；第二，各模型在相同分位数下的RQ值相差不大，但AS模型在所有分位点水平下均具有最小的RQ值；第二，系数β2基本上都是高度显著的，这说明尾部分位数的波动聚集效应是显著存在的，而且它的值均保持在0.8以上，尤其是右尾β2的取值均在0.94以上，这说明了VaRt具有非常强的短期记忆性，且右尾比左尾的强度更大；第三，针对外部冲击不具有非对称效应的SAV模型和IGARCH模型，右尾系数β3在0.1的显著性水平下均显著，而左尾系数β3部分显著，说明外界信息冲击对于未来隔夜收益的分位数预测具备相当的解释能力，但在左、右尾的表现具有明显的差异。一旦将外部冲击分解为正面和负面收益消息时，β3系数在左尾分位数上部分显著，在右尾分位数全部显著，而β4系数绝大部分是显著的，这在一定程度说明多头方和空头方在对待外界消息冲击时的敏感程度是不一致；第四，针对非对称结构的AS模型，从外界消息冲击对当期VaR的影响方向来看，股指隔夜收益的上涨和下跌均会加大下一期的VaR值，换言之，隔夜收益的上涨和下跌会显著地加大下一期的隔夜风险。

总而言之，无论是从RQ值和样本内DQ统计量值，我们发现具有杠杆效应的AS模型要比SAV模型和IGARCH模型表现更佳，它能更好地描述普通隔夜风险的动态特征。

表2 模型左尾分位数估计结果

表3 模型右尾分位数估计结果

4 模型的后测检验方法及结果分析

4.1 后测检验方法说明

为了检验上述各模型的样本动态VaR预测精度，Kupiec[16]提出了一种VaR失败率(Failure Rate)的似然比检验方法，为了进行该检验，首先定义“击中序列”(Hit Sequence)hitt,以多头VaR为例，定义如下：

(5)

它表示的是，如果t时刻的实际收益超出所估计的VaR值，称为一次击中事件，那么该序列t时刻的取值为1，否则为0。假设该模型能有效地预测隔夜风险，则该“击中序列”应服从贝努利分布。在模型没有误设的零假设下，构造似然比的非条件检验统计量：

(6)

其中，p为显著性水平，N为预测的样本总数，n为预测样本中的失败次数。通过(6)式可知道Kupiec检验量是刻画实际失败次数接近理论失败次数程度的指标。当LR统计量大于给定置信水平下卡方分布的临界值，则拒绝原模型。相反，当统计量小于临界值，则接受该模型。

但是，Kupiec似然比检验只是检验实际击中比率与理论击中比率的接近程度。进一步的研究表明，除了检验失败比率以外，还应检验VaR失败值之间是否存在相关性[9,17]，如果发生VaR预测失败的观测值之间具有明显的相关性，那么有可能发生连续超过VaR的损失，这将给投资者带来巨大的损失，也就是说，精确可靠的风险测度模型的击中序列应该是无偏和无自相关的。由此，Engle和Manganelli[9]提出了动态分位数检验(Dynamic Quantile test，DQ test)，以多头风险为例，该检验首先定义一个新的击中序列：

HITθ,t=I(yt<-VaRt)-θ

(7)

其中，θ为给定的分位数，当yt<-VaRt时，HITθ,t=1-θ；当yt>-VaRt时，HITθ,t=-θ。显然，如果模型参数估计正确，那么E(HITθ,t|Ωt-1)=0。这说明HITθ,t对于任何滞后的HITθ,t-k以及预测的VaRt-k都应不具备相关性，构造如下回归方程：

HITθ,t=β0+β1HITθ,t-1+β2HITθ,t-2+……+βpHITθ,t-p+βp+1VaRt+ut

(8)

把上述模型表述成矩阵形式：HITθ,t=Xβ+ut，其中X是T×K矩阵向量，借鉴淳伟德等[18]的做法，取p=5,k=7。在原假设：β=0的情况下，构造的DQ检验统计量为：

(9)

4.2 普通隔夜风险的后测检验分析

从表4两个后测检验结果可以看出：在5%的显著性水平下，三个模型仅在0.95的分位数下均无法通过样本外DQ检验，似然比检验则全部通过，说明本文给出的这三个CAViaR模型整体能很好地描述常规分位数水平上隔夜风险的动力学特征；在表4相应的12组估计结果中，AS模型只获得6次并行的最优风险预测精度，IGARCH获得5次，SAV模型则只有3次，结合表(2)(3)的估计结果可知，AS模型在普通分位数的多空头VaR预测方面表现最优。而SAV模型和IGARCH模型整体表现次之，两者无绝对的优劣之分。

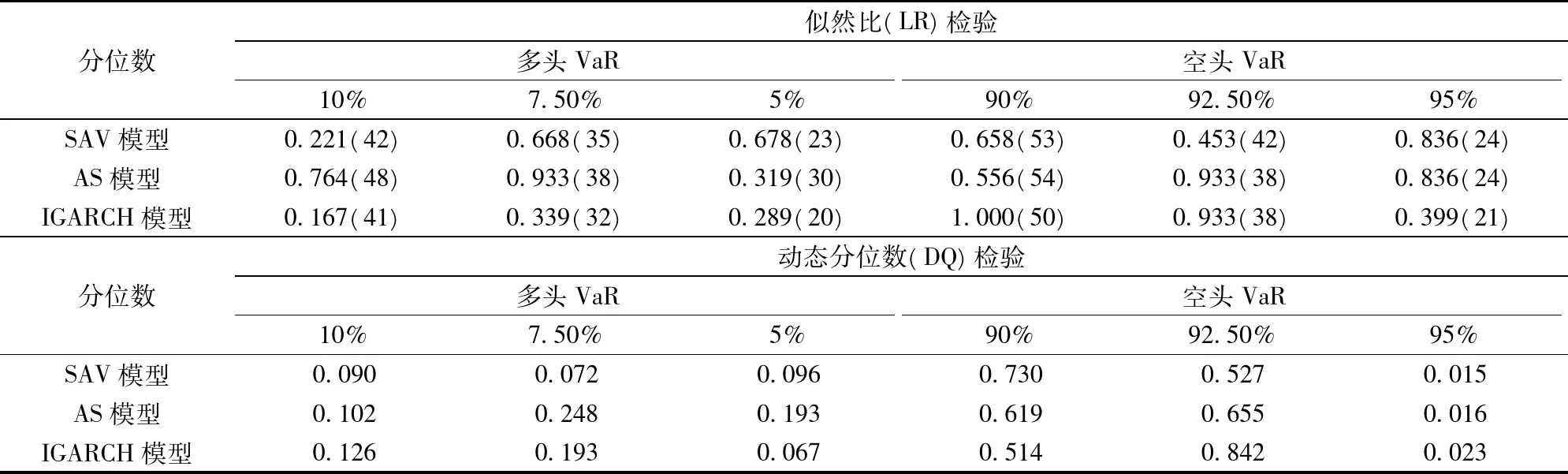
表4 模型的后测检验结果

5 极端隔夜风险的预测

对于极端分位数(如0.5%或0.1%)的估计，由于半参数CAViaR模型进行最优化时可利用的数据极少，如果直接采用CAViaR模型对低分位数VaR进行估计，势必会造成结果不可靠乃至偏差。目前国内针对极端尾部风险度量的方法主要有EVT-POT和GARCH-EVT两种，但是极值理论要求原始数据为独立同分布，且阈值的选择具有一定的主观性，而金融收益数据往往难以满足其要求；GARCH-EVT模型虽然对原始收益数据进行了一定程度的过滤，但究竟选择何种收益分布和波动率方程目前也没有共识。为此，Manganelli和Engle[19]在理论上构建CAViaR-EVT模型，但该模型仍未用于实证研究，该方法结合了CAViaR模型处理常规分位数的优势，以及极值理论处理尾部风险的稳健性，因此该模型在计算低分位数风险价值时更具可靠性。由于极端隔夜风险对于期货投资者而言意义重大，如不能很好的防范将遭受巨大的损失，因此这部分采用CAViaR-EVT模型对极端隔夜风险进行分析预测。

5.1 CAViaR-EVT模型的构建

为节省篇幅，本文以左尾分位数为例(右尾推导过程类似)，具体阐述CAViaR-EVT模型估算极端隔夜风险的步骤如下：

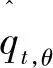
(10)

然后，由于标准化的残差序列有效地削弱了原始数据的自相关性，因此更适合运用极值理论。现仅假设标准化的分位数残差序列右尾具有独立同分布性质，通过(11)可将求解原始收益数据的p分位数转换为求解标准化残差序列的(1-p)分位数：

Pr(ytqt,p/qt,θ-1)=p

(11)

(12)

其中ξ代表形状参数，而σ代表尺度参数，ξ>0时说明广义帕累托分布是厚尾的。当尾部数据很少时，POT仍然具有较强的稳健性，因而本文考虑使用EVT中的POT模型对极端尾部进行建模分析。

POT模型关键是确定最优的门槛值，阈值的选取通常有两种方法：一是根据Hill图；二是依据超额期望函数图。本文采用第二种方法。将样本值按从大到小排列，即X(1)>X(2)>…>X(n)，样本的超额期望函数定义为：

(13)

确定阈值后，超过阈值u的超额数分布函数为:

(14)

对于充分高的阈值，超过阈值的数据近似服从GPD分布(Generalized Pareto Distribution)，即有Fu(y)≈Gξ,σ，由(14)式可得分布的尾部累积分布函数为：

F(x)=(1-F(u))Gξ,σ(x-u)+F(u) (x>u)

(15)

假设超过阈值的样本个数为Nu,总样本数为n，采用(n-Nu)/n替换F(u)，并运用极大似然法估计出相关的参数ξ、σ，最后经过相关推导可得到置信水平p下的VaR值：

(16)

5.2 极端隔夜风险的后测检验分析

利用POT方法计算VaR时首先必须确定适当的阈值，选择合适阈值的标准是使得超限期望函数在大于阈值时近似为正斜率的线性函数，根据公式(13)，得到隔夜收益的标准化残差序列的超限期望图，从而确定最优阈值，再使用极大似然估计方法求出GPD分布的参数。表5给出了由(15)计算出的标准化残差序列的相关估计结果，可以看出，阈值u在[0.0178，0.0498]区间，系数ξ在所有模型中均为正，说明标准化残差序列具有显著的厚尾性。

求得上述结果后，利用(16)式得到标准化残差序列的VaR值，最后根据残差与原始序列的关系得出隔夜收益对应置信水平下的VaR值。

表5 标准化残差序列EVT-POT估计结果

表6 极端分位数的后测检验结果

为了进行简单的对比，表6给出了CAViaR-EVT模型、EVT和GARCH-EVT三种不同模型的后测检验结果：(1)从Kupiec似然比检验结果来看，所有模型在95%的置信水平下均拒绝原模型；然而，动态分位数检验结果不如Kupiec 似然比检验理想，EVT模型对右尾的三个分位数上都被拒绝，但其他的分位数都高度显著，至于DQ检验出现很多相同的P值，且P值的波动性相当大，主要是因为CAViaR模型在预测极端分位数下VaR出现的失败次数很少，甚至为0，最终使得HITθ,t序列容易出现强自相关或无自相关这两种极端的情况；(2)CAViaR-EVT中的三个模型通过了所有的后测检验，且预测精确度表现优异，但三者之间没有哪一个模型展现出绝对的优势，三者均能良好的刻画我国股指期货极端隔夜风险的动态变化过程。由于CAViaR模型无须设定误差分布函数的特定形式，在计算普通分位数的VaR表现优异，而EVT-POT方法能准确捕捉尾部分布特征，两者的结合更有利于准确分析极端事件对金融市场造成的冲击和影响；(3)从似然比检验的失败次数来看，基于EVT 的静态VaR 模型在估计风险时过于保守，过高估计了风险，造成了资金使用的无效率，同时它也无法规避VaR击中事件的相关性问题。GARCH-EVT模型也存在高估隔夜风险的问题。总体而言，本文提出的CAViaR-EVT模型的预测精度要优于EVT和GARCH-EVT模型，它能更准确分析极端事件对金融市场造成的冲击和影响，以便预测极端波动风险。

6 结语

沪深300股指期货作为我国交易最活跃的期货品种，其隔夜风险测度和防范一直是企业界和监管部门关注的热点。本文以沪深300股指期货当月连续合约为例，深入研究了隔夜收益的统计特征及波动模式，并采用了半参数法的CAViaR模型刻画了沪深300股指期货多头和空头在不同分位数的VaR动态特征，并首次运用CAViaR-EVT模型来对极端隔夜风险进行预测，最后运用后测检验中的Kupiec似然比检验和动态分位数检验对不同风险模型的测度精度进行比较。通过实证得出以下结论：

第一，从整个样本期变动趋势看，隔夜收益在上市前期表现出较大的价格波动，后期则日趋平稳，而后又出现阶段式的大幅波动。从隔夜收益序列自身特性来看，它呈现出右偏和尖峰厚尾特性、缺乏长期记忆性，且跳空上涨的概率比跳空下跌的概率要大等性质。

第二，CAViaR模型对我国股指期货市场的普通隔夜风险具有优异的预测能力。通过严谨的后测检验结果看出，AS模型在预测普通隔夜风险上要优于IGARCH模型和SAV模型，而SAV模型和IGARCH模型之间无明显的优劣之分。

第三，为了预测极端分位数下的隔夜风险VaR，本文巧妙地结合极值理论和CAViaR方法的优势构造出CAViaR-EVT模型，通过与EVT和GARCH-EVT模型对比发现，该模型对动态极端隔夜风险VaR同样具有良好的预测精度。

目前我国期货市场相比发达的期货市场而言还处于初步发展阶段，制度不完善、国际定价权缺乏和投机心理严重，使得我国期货市场极易受到复杂多变的国际国内金融环境影响。而且期货作为一种金融衍生产品，其面临的隔夜风险会被成倍的放大，那么如何有效地管理隔夜风险必定是业界和理论界密切关注的热点。值得一提的是，本文采用的CAViaR模型在一定程度上能够很好的度量和预测沪深300股指期货普通隔夜风险和极端隔夜风险，文中的结论有助于投资主体更好地认识隔夜风险，也可以为中国股指期货投资者和监管部门开展有效的风险管理及监督活动提供理论参考。

[1] Del C W, Colwell D, Michayluk D, et al. News releases when markets are closed[R].Working Paper, University of Technology Sydney, 2003.

[2] Andersen T G, Bollerslev T. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts[J].International Economic Review, 1998, 39(4)：885-905.

[3] Hansen P R, Lunde A. A realized variance for the whole day based on intermittent high-frequency data[J].Journal of Financial Econometrics, 2005, 3(4)：525-554.

[4] Koopman S J, Jungbacker B, Hol E. Forecasting daily variability of the S&P 100 stock index using historical, realised and implied volatilitymeasurements [J].Journal of Empirical Finance, 2005, 12(3)：445-475.

[5] Andersen T G, Bollerslev T, Huang Xin. A reduced form framework for modeling volatility of speculative prices based on realized variation measures[J].Journal of Econometrics, 2011, 160(1)：176-189.

[6] Taylor N. A note on the importance of overnight information in risk management models [J].Journalof Banking & Finance, 2007,31(1)：161-180.

[7] 刘庆富,张金清.中国商品期货隔夜信息对日间交易的预测能力[J].管理科学学报,2013, 16(11)：81-94.

[8] 简志宏,李彩云.隔夜风险可以预测吗?——基于HAR-CJ-M模型的高频数据分析[J].管理评论,2014,26(2)：5-14.

[9] Engle R F，Manganelli S. CAViaR: Conditional autoregressive value at risk by regression quantile[J].Journal of Business and Economic Statistics, 2004, 22(4)：367-381.

[10] Huang Dashan, Yu Baimin, Fabozzi F J, et al. CAViaR-based forecast for oil price risk[J].Energy Economics, 2009, 31(4)：511-518.

[11] Huang Dashan, Yu Baimin, Lu Zudi, et al. Index-exciting CAViaR: A new empirical time-varying risk model[J].Studies in Nonlinear Dynamics & Econometrics, 2010, 14(2)：1-24.

[12] 闫昌荣.基于流动性调整CAViaR模型的风险度量方法[J].数量经济技术经济研究，2012，(3)：151-161.

[13] 陈磊,曾勇,杜华宇.石油期货收益率的分位数建模及其影响因素分析[J].中国管理科学，2012,20(3)：35-40.

[14] 陈磊,杜化宇,曾勇.基于贝叶斯CAViaR模型的油价风险研究[J].系统工程理论与实践,2013,33(11)：2757-2765.

[15] Koenker R, Bassett Jr G. Regression quantiles[J]. Econometrica, 1978, 41(1)：33-50.

[16] Kupiec P H. Techniques for verifying the accuracy of risk measurement models[J].Journal of Derivatives, 1995, 3(2)：73-84.

[17] 魏宇.基于多分形理论的动态VaR预测模型研究[J].中国管理科学,2012,20(5)：7-15.

[18] 淳伟德,陈王,潘攀.典型事实约束下的上海燃油期货市场动态VaR测度研究[J].中国管理科学,2013,21(2)：24-31.

[19] Manganelli S, Engle R F. Value at risk models in finance[R]. Working Paper,Frankfurt am Main: European Central Bank, 2001.

[20] McNeil A J, Frey R. Estimation of tail-related risk measures for heteroscedastic financial time series: An extreme value approach [J].Journal of Empirical Finance, 2000, 7(3)：271-300.

[21] Longin F M. From value at risk to stress testing: The extreme value approach[J].Journal of Banking & Finance, 2000, 24(7)：1097-1130.

Study on CSI 300 Stock Index Futures Overnight Risk Based on CAViaR Model

JIAN Zhi-hong1,ZENG Yu-feng2,LIU Xi-teng3

(1.School of Economics HUST,Wuhan 430074,China;2.School of Economics,Fudan University,Shanghai 200433,China; 3.School of Public Economics and Administration,Shanghai University of Finance and Economics,Shanghai 200433,China)

Financial futures market is an important part of modern financial market systems in China. However, financial derivatives have natural properties of high-yield and high risk.Once a futures risk event occurs, it will cause great destructive effect to the whole financial markets.So investors have always been paying great attention to the prevention of futures' overnight risk. However, little work has been done to detect volatility characteristics and risk features of overnight return.By taking CSI300 stock index futures for sample in this paper,CAViaR model is adopted to directly calculate the common VaR of overnight return. Nevertheless, considering rare data available during optimization in extreme quantiles, the estimation results may be biased. Therefore, a new framework, which combining extreme value theory and CAViaR model, is built to estimate the extreme overnight risk and analyze the dynamic characteristic of different quantiles both in left tail and right tail.Then both Kupiec LR(likelihood ratio) test and dynamic quantile test are used to backtest the accuracy of these models.The empirical results are summarized as follows: (1) overnight return exhibits stylized facts of positive skewness, leptokurtosis and non-normal distribution. But it lacks of long-term memory property. (2) The three CAViaR models have strong predictivity power to the common overnight risk, among which the AS model performs best, while there is no significant difference between SAV model and IGARCH model. (3) After adding the extreme theory to the CAViaR model, the newly-constructed CAViaR-EVT model still can accurately depict the dynamic process of overnight risk in extreme low quantiles. Moreover, its forecast results are more reasonable than EVT model and GARCH-EVT models.Important practical and social implications are suggested. The CAViaR model and CAViaR-EVT model offer useful practical approaches to forecast futures' overnight risk. Moreover, it also provides a theoretical reference to carry out effective risk management and monitor activities for the Chinese stock index futures investors and regulators, such as position limits and margin ratio.

overnight risk；CAViaR model；CSI300 stock index futures；value at risk

2015-06-24；

2016-04-01

中央高校基本科研业务费资助项目(2016AB008)

简介：曾裕峰(1990-)，男(汉族)，江西吉安人，复旦大学经济学院博士研究生，研究方向：金融风险管理，E-mail：zyf_2014@126.com.

F830.91

A

1003-207(2016)09-0001-10

10.16381/j.cnki.issn1003-207x.2016.09.001