基于评价结论的二次组合评价方法研究
2016-12-28彭张林王素凤杨善林
彭张林,张 强,王素凤,杨善林
(1.合肥工业大学管理学院,安徽 合肥 230009;2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009;3.安徽建筑大学管理学院,安徽 合肥 230601)
基于评价结论的二次组合评价方法研究
彭张林1,2,张 强1,2,王素凤3,杨善林1,2
(1.合肥工业大学管理学院,安徽 合肥 230009;2.过程优化与智能决策教育部重点实验室,安徽 合肥 230009;3.安徽建筑大学管理学院,安徽 合肥 230601)
针对不同的组合评价方法所获取的一次组合评价结果依旧存在不一致性和收敛性较差等问题,提出了“二次组合评价”的概念,并研究了一种基于评价结论的二次组合评价方法。给出了该方法的关键流程和实现步骤,主要包括综合评价问题描述,单一评价方法的问题描述,组合评价方法的问题描述,评价结论的一致性分析,基于偏移度最小的二次组合评价方法选取以及二次组合评价的收敛性分析,并通过算例对本文提出的二次组合评价方法进行分析,案例研究结果表明二次组合评价结果的误差要远小于各一次组合评价结果的误差,与一次组合评价相比,二次组合评价的组合效果更好,有效性更强。通过二次组合评价可以有效提高一次组合评价的一致性和收敛性,降低一次组合评价的组合误差,提高综合评价整体评价结论的可信度。
综合评价;组合评价;评价方法;评价结论
1 引言
在综合评价过程中,主要存在组合赋权,专家信息的组合(群决策),指标构建方法、赋权方法、数据处理方法、信息融合方法和检验方法的综合运用,以及评价结论的组合四类组合问题。目前,对于前三类组合问题,国内外学者开展了很多研究工作,例如:陈衍泰等[1-3]分别研究了一种主观权重和客观权重相结合的赋权方法;闫书丽等[4-6]研究通过信息融合方法将多个专家的知识、意见和偏好进行信息集成;文献[7-9]主要研究针对特定的评价问题在其评价过程的不同阶段采用不同的评价方法,然后综合利用和综合分析各阶段的信息处理结果。然而,基于评价结论的组合其本身也是一类重要的组合问题。这是由于主成分分析法、因子分析法、模糊综合评价方法、灰色关联度分析法、可拓决策评价方法、熵值法、证据推理、Topsis法、AHP/ANP、DEA、神经网络等综合评价方法在指标预处理、数据选用、权重系数设置以及信息集结模型选取等内在机理上存在不同,使得它们在评价过程中所抓住的“信息源”和“信息量”存在差异,进而使得评价往往只侧重于一个或几个方面,关注的不全面,评价结果往往具有片面性,从而引起评价结论的非一致性问题[10-11]。为了更完整地捕捉“信息源”和“信息量”,“组合评价”应运而生。然而,对于基于评价结论的组合评价问题,国外学者[12-14]主要侧重从理论层面提出一些框架和构想,国内学者[15-19]多从方法层面和应用层面展开,且国内相关研究要偏多。组合评价是将多种单一评价方法得到的评价结论进行组合,以减少评价过程中的随机误差和系统偏差,并最大限度地利用多评价结论的信息,用以提高评价结论的准确性和可信度[17]。其基本思想是,对有代表性的几种评价方法的评价结果采用适当的思想或方法进行组合,得出评价值,按组合评价值的大小得到组合评价的排序结果[20-21]。
现有对组合评价方法的研究主要集中于评价权重的组合[1, 22-25]和评价结论的组合[15, 26-27]两个方向。其中评价权重的组合又分为区分主客观权重的组合[28-29]和不区分主客观权重的组合[30]两类;评价结论的组合又分为序值组合[15, 31-32]和评价值组合[17, 33-35]两类。对比研究发现,运用评价值进行组合较评价权重的组合更直接,同时避免了权重组合结果带来的偏差;而与序值组合相比较而言,评价值组合拥有更大的信息量,使得组合评价值更接近真实值。
常见的组合评价方法有平均值法、Borda法、Copeland法与离差最大化方法等优化组合方法[36-37]。这些组合评价法为解决单一评价方法产生的非一致性问题提供了一种思路,但由于不同的组合评价方法其组合机理的不同,其组合评价值也不一样,由此可能会产生新的不一致性以及组合结论收敛性较差的问题。要解决该问题,目前最常用的解决方法是对各单个组合方法评价结果的有效性进行比较,以确定哪一种组合评价方法在什么情况下更有效。但有效性比较只是抓住了组合评价相对“最优”的信息,遗漏了“次优”等其他信息,使得综合评价结果的准确性和可靠性大打折扣。针对这种情况,陈衍泰[20]和陈国宏等[38]提出了复组合评价的概念并给出了复组合收敛性的定义以及其计算实验过程,复组合评价的理论基础还是组合评价,是在一次评价的基础上,进行第二次、第三次、甚至是多次组合,其最终目标是通过多次组合,实现评价结论的一致性和收敛性。
复组合评价为解决一次组合评价的非一致性问题和收敛性问题提供了一个较好的思路,但目前关于复组合评价和多次组合评价的研究比较少,而陈衍泰[20]和陈国宏[38]等有限的研究还存在以下几个问题:一是复组合评价方法的选取问题,一般情况下复组合评价是采取相对较优的组合评价方法对原先的评价结论进行再组合,但是如何确定哪种方法较优,目前的研究并没有给出一个标准和解决方案;二是复组合评价次数的问题,逻辑上说,复组合评价可以无限制地组合下去,但是否组合次数越多,组合效果就越好,对于一个组合评价问题,其组合次数该如何确定;三是复组合评价多停留在理论探索阶段,从事实证研究的相对较少;四是复组合评价现在尚未形成一个系统性的方法体系。
为此,本研究首先在“组合评价”思想和“复组合评价”概念的基础上,提出“二次组合评价”的概念,二次组合评价,是选择最优的组合评价方法对一次组合评价的结论进行再次组合,旨在通过“二次组合评价”强化对“次优”信息的充分利用,提高一次评价的一致性和收敛性;其次,建立了基于偏移度最小的二次组合评价方法的选取规则;再者,给出了“二次组合评价”的方法体系,以期为“复组合评价”或“多次组合评价”的进一步扩展奠定一些理论与方法基础;最后,通过算例对本研究构建的“二次组合评价”的方法体系进行验证。
2 二次组合评价方法模型
基于评价结论的组合评价,是运用某种思想或方法将各单一评价方法获取的评价结果以某种形式组合起来,以达到优化的目的,使组合评价的结论尽可能地贴近真实值,提高评价结果的真实性和可靠性。二次组合评价是在组合评价的体系框架下,基于对一次组合评价结论一致性分析的基础上,选取相对最优的组合评价方法对一次组合评价结论进行再组合,以最终获取多指标多方案综合评价问题的评价值。二次组合评价方法关键流程如图1所示。
2.1 多指标多方案综合评价问题描述
在某一多指标多方案的综合评价问题中,假设有m个待评对象或评价方案,每个待评对象或评价方案都有l个评价指标,则定义S={S1,S2,…Sm}为评价对象集,I={I1,I2,…,Il}为评价指标集。令yik表示第i个评价对象Si对第k个评价指标Ik规范化后的评价值,则Y=(yik)m×l为该评价问题的评价效用矩阵,其中,i=1,2,…,m;k=1,2,…,l。
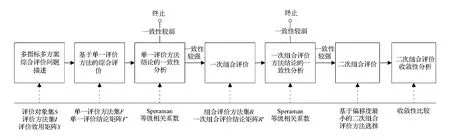
图1 二次组合评价方法流程
对于该评价问题,决策者需要通过相应的评价思想或方法,获取全部评价对象的评价值,并根据评价值对评价对象进行排序,以实现评价对象的排序和优选。
2.2 基于单一评价方法的问题描述
针对以上描述的多指标多方案的综合评价问题,可以结合该评价问题的指标特性、数据特征,选用不同的单一评价方法。但由于在实施组合评价时,要考虑到不同方法之间的相容性,就有必要针对不同方法的属性、内在机理和适用范围等因素,选取具有可比基础、能够组合的单一评价方法。因此,选取n个可相容的单一评价方法,建立方法集F={F1,F2,…Fn}。令fij为用第j种评价方法获取的第i个评价对象的评价值,其中,i=1,2,…,m;j=1,2,…,n。则用方法集F中的各单一评价方法分别对全部评价对象实施评价,可以得到全部评价方法对应的全部评价对象的评价结果矩阵F*=(fij)m×n。
2.3 基于组合评价方法的问题描述
虽然评价方法集F={F1,F2,…Fn}中所选取的方法间具有一定的相容性,但不同的方法其内在机理和属性还是存在差异,这种差异使得不同方法在评价过程中所抓住的“信息源”和“信息量”存在差距。因此,为了更完整地捕捉“信息源”和“信息量”,需要选用合适的组合评价思想或方法对各单一评价方法所获取的评价结论实施组合。单一评价方法获取的评价结论通常是以评价值或序值的方式给出,针对评价值或序值的特点,选取r个组合评价方法,建立组合评价方法集R={R1,R2,…,Rr}。令rit为用第t种组合评价方法组合后得到的第i个评价对象的组合评价值,其中,i=1,2,…,m;t=1,2,…,r。则用评价方法集R中的组合评价方法分别对单一评价方法获取的评价结果矩阵F*=(fij)m×n进行组合评价,可以得到组合评价的结果矩阵为R*=(rit)m×r。
2.4 评价结论的一致性分析
不同的组合评价方法得到的组合结果必然存在一定的差异,但是对于同一个样本集来说,其差异性不宜太大[39],故在进行二次组合评价之前,需要对r个组合评价方法所获取的一次组合评价结果进行一致性检验。可采用非参数统计方法——等级相关系数,来检验不同评价方法评价结果的密切程度。本研究选用Spearman等级相关系数对不同组合评价方法的组合结果进行一致性分析。Spearman等级相关系数公式如下:
(1)
其中,di为在第s个和第t个两种组合评价方法下排序的等级差,其中,s=1,2,…,r,t=1,2,…,r。当rst>0时,表明两个方法之间具有正相关;当rst<0时,表明两个方法之间具有负相关;当rst=0时,表明两个方法不相关。
2.5 基于偏移度最小的二次组合评价方法的选择
在进行二次组合评价之前,需要选择和确定一个合适的二次组合评价思想和方法,建立一个二次组合评价的准则,对一次组合评价的结果进行再组合。如何确定一个合适或最优的二次组合评价准则,一般很难找到一个客观的选择标准,因此也就很难证明哪一种方法更为合理和准确。通常情况下,决策者认为评价对象的测量值与真实值之间的差距越小,其评价结果的可信度和可靠性就越高。但是在现实实践中,综合评价问题的真实值比较难以确定。有学者利用计算机仿真实验,通过大量不同类型数据在多种单一方法下的仿真实验,找到一个统计意义上的“评价对象的真实值”,并用该统计意义上的“真实值”与“测量值”进行比较,以判断哪种方法的效度较高。本研究首先根据统计理论,用全部评价值的简单算术平均值作为一个基准,来表示评价对象的“真实值”;其次提出“偏移度”的概念,并用其来测量某种组合评价方法获取的组合评价值相对于被评对象真实值之间的偏移程度,反映了被评对象测量值与真实值之间的差距;接着根据误差理论,用误差平方和来测量“偏移度”,“偏移度”最小的组合方法即为最优的方法。基于此,建立基于偏移度最小的二次组合评价方法的优选规则如下:
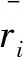
(2)
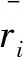
(3)
3、比较全部组合评价方法下,组合评价结果的误差平方和大小。首先,计算全部组合评价方法下组合结果的误差平方和,并比较其大小,min(SSEt)(其中,t=1,2,…,r)表示误差平方和最小者min(SSEt)对应的组合评价方法,其组合结果的偏移度最小,该方法相对最优。
4、实施二次组合评价。选择min(SSEt)对应的组合评价方法对一次组合评价的结果进行二次组合评价。
2.6 二次组合评价的收敛性分析
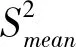
3 算例分析
3.1 算例选取
我们在李珠瑞等[10]和彭张林等[40]中研究了一种基于离差最大化的组合评价方法,并以2008年全国各地区规模以上工业企业经济效益评价做了实例研究。该研究主要提出了一种离差最大化的组合评价模型,并用该模型对分别用主成分分析法、熵值法和因子分析法评价得到的2008年全国各地区规模以上工业企业经济效益的评价结果进行组合,然后将组合结果与平均值组合法和模糊Borda组合法得出的组合结果进行了比较分析。本文将以该研究为基础,利用其测算的相关数据,围绕上述构建的二次组合评价模型进行二次组合评价的算例分析。
在李珠瑞等[10]和彭张林等[40]中,对我国各地区规模以上工业企业经济效益的评价主要围绕总资产贡献率、资本负债率、工业成本费用利润率、流动资产周转次数和产品销售率等5个指标进行评价并以2008年国家统计局公布的统计资料和数据为例,对北京、天津等31个省市自治区的规模以上工业企业经济效益进行评价。在具体评价过程中,首先,选用了具有相容性特征的主成分分析法、熵值法和因子分析法三种单一评价方法分别进行了单一评价;其次,利用离差最大化组合评价方法、平均值组合法和模糊Borda法分别进行了一次组合评价。故对于该综合评价实例,我们可知其评价对象集为S={S1,S2,…S31},分别表示北京、天津、河北、山西、……、青海、宁夏和新疆等31个省市自治区;评价指标集I={I1,I2,I3,I4,I5},分别表示总资产贡献率(%)、资本负债率(%)、流动资产周转次数(次/年)、工业成本费用利润率(%)和产品销售率(%);单一评价方法集F={F1,F2,F3},分别表示主成分分析法、熵值法和因子分析法;组合评价方法集R={R1,R2,R3},分别表示平均值组合法、模糊Borda法和离差最大化组合评价方法。
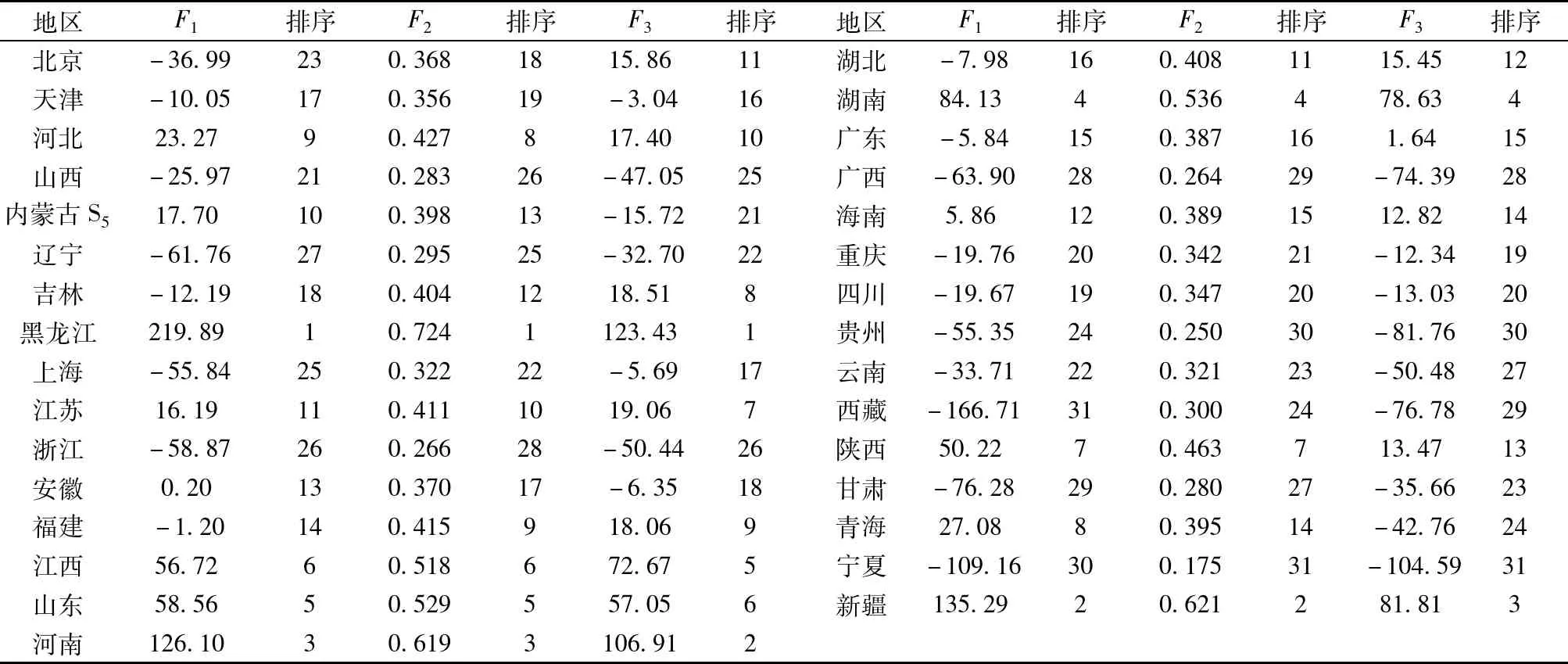
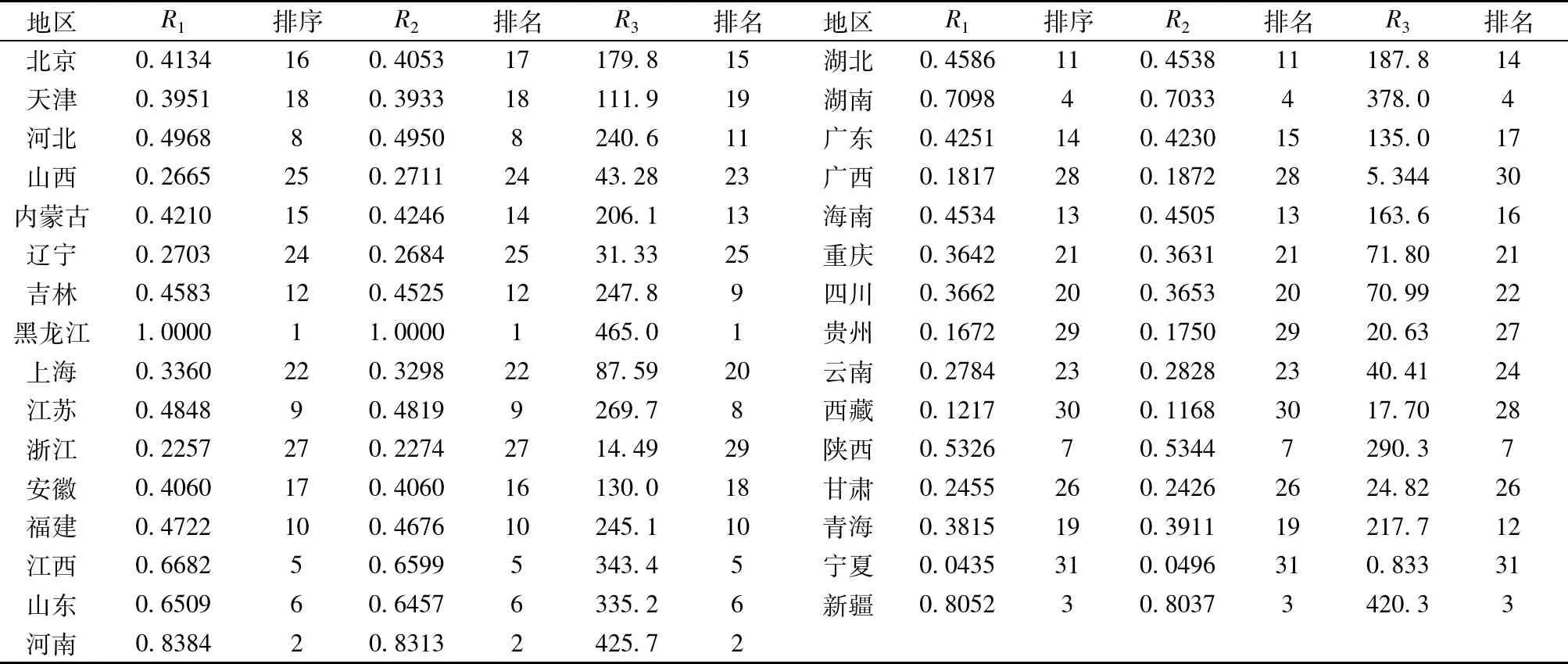
2008年全国各地区规模以上工业企业主要经济效益指标的原始数据、单一评价方法的评价结果和一次组合评价的组合结果分别见表1、表2和表3。
3.3 基于斯皮尔曼等级相关系数的一致性检验
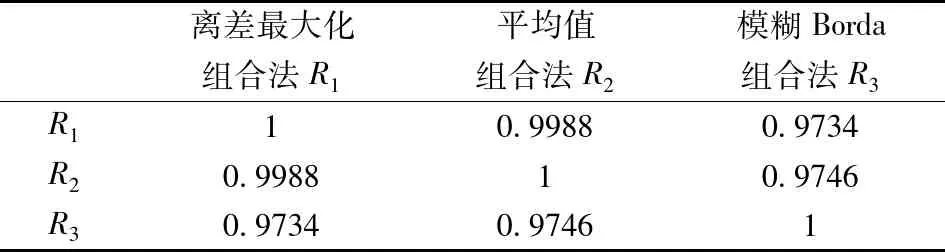
从表2和表3可以看出,用三种不同的单一评价方法和三种不同的组合评价方法分别获取的2008年31个省市自治区规模以上工业企业经济效益的评价值和排序结果存在一定的差异。为了验证一次组合评价的可靠性和二次组合评价的可行性,根据表2和表3中的数据,利用Spearman等级相关系数,分别对主成分分析法、熵值法和因子分析法3个单一评价方法以及平均值法、模糊Bordda法和离差最大化法3个组合评价方法的一致性进行检验。
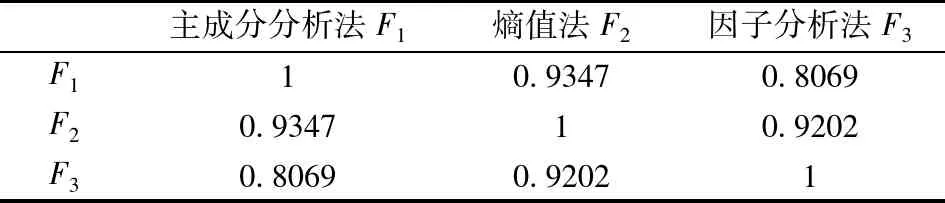
由表4可以看出,运用主成分分析法、熵值法和因子分析法3个单一评价方法求取的2008年我国31个省市自治区规模以上工业企业经济效益评价结果的Spearman等级相关系数分别为r12=0.9347,r13=0.8069,r13=0.9202。由此可知,主成分分析法、熵值法和因子分析法这3个单一评价方法具有明显的正相关关系,且相关系数很高,表明这三种方法具有较好的一致性,符合一次组合评价对评价方法集的相容性和一致性要求。
3.4 二次组合评价的方法选取与计算
通过一致性检验可知,运用离差最大化组合评价方法、平均值组合评价方法和模糊Borda组合评价方法这三种方法获取的组合结果一致性非常高,符合进一步进行二次组合评价的一致性要求。接下来,利用基于偏移度最小的二次组合评价方法的选择规则,从离差最大化组合评价方法、平均值组合评价方法和模糊Borda组合评价方法这三个方法中选择一个相对较优的方法,对一次组合评价的结果进行第二次组合评价。
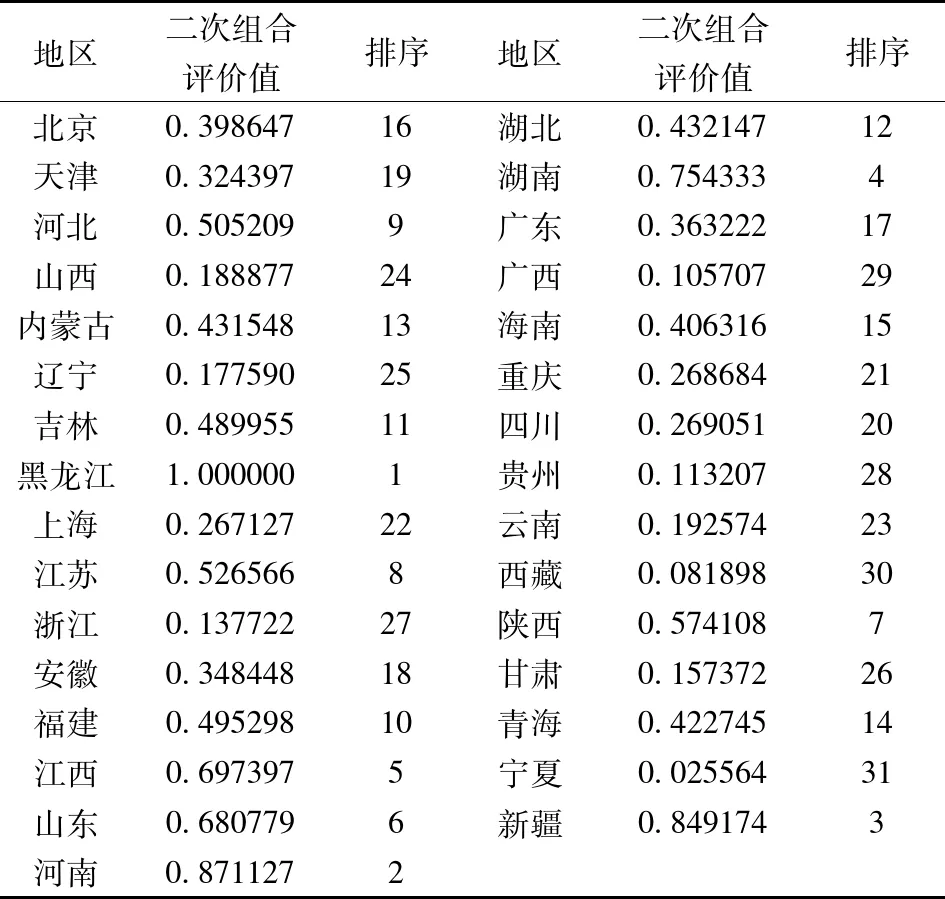
通过2.5中介绍的规则,可以求出离差最大化组合评价方法、平均值组合评价方法和模糊Borda组合评价方法这三种组合评价方法的组合误差平方和分别为SSE1=0.054728,SSE2=0.056515和SSE3=0.221767,易知SSE1 表1 2008年全国各地区规模以上工业企业主要经济效益指标数据 表2 2008年全国各地区规模以上工业企业经济效益基于单一评价的结果 表3 2008年全国各地区规模以上工业企业经济效益一次组合评价结果 表4 单一评价方法评价结果Spearman等级相关系数矩阵 表5 一次组合评价结果Spearman等级相关系数矩阵 表6 2008年全国各地区规模以上工业企业经济效益二次组合评价结果 3.4 二次组合评价的有效性比较 由于该算例只是从一次组合评价的3个方法中选取了一种相对最优的组合评价方法对一次组合评价的结果了进行二次组合评价,并不是分别再次用该3个方法对一次组合评价的结果再进行全部组合。因此,在这里我们不比较二次组合评价的结果与一次组合评价的结果收敛性,而是通过偏差平方和去测量“组合值”与“真实值”之间的偏差,并以此来比较一次一次组合评价结果与二次组合评价结果的组合效果。 考虑到不同的组合评价方法会产生新的不一致性问题和组合结果收敛性较差的问题,本文在“组合评价”思想和“复组合”概念的基础上,讨论了基于评价结论的二次组合评价方法,描述了二次组合评价模型的方法流程主要包括多指标多方案的综合评价问题描述、单一评价方法的问题描述、组合评价方法的问题描述、一次组合评价结果的一致性分析、基于偏移度最小的二次组合评价方法的选择和二次组合评价的收敛性与有效性分析等内容。最后,通过算例对本文建立的二次组合评价模型的有效性进行了验证,算例结果显示二次组合评价结果的误差要远小于各一次组合评价结果的误差,与一次组合评价相比,二次组合评价的组合效果更好。论文的核心工作主要有:一是首次提出了“二次组合评价”的概念,并进行了定义;二是建立了基于偏移度最小的二次组合评价方法的选取规则;三是构建了“二次组合评价”的方法体系和关键流程。研究结果表明基于评价结论的二次组合评价方法可以有效提高一次组合评价结论的一致性和收敛性,降低一次组合评价的组合误差,提高综合评价整体评价结论的可信度。当然,今后还将通过大量的案例对该方法做更深入的分析和验证。 [1] 陈衍泰, 陈国宏, 李美娟. 应用合作博弈确定组合评价权重系数的方法研究[J]. 中国管理科学, 2005, 13(3): 89-94. [2] Song Wenyan, Ming Xinguo, Wu Zhenyong, et al. Failure modes and effects analysis using integrated weight-based fuzzy TOPSIS[J]. International Journal of Computer Integrated Manufacturing, 2013, 26(12): 1172-1186. [3] Zhang Hongyu, Ji Pu, Wang Jianqiang,et al. An improved weighted correlation coefficient based on integrated weight for interval neutrosophic sets and its application in multi-criteria decision-making problems[J]. International Journal of Computational Intelligence Systems, 2015, 8(6): 1027-1043. [4] 闫书丽, 刘思峰, 方志耕,等. 区间灰数群决策中决策者和属性权重确定方法[J]. 系统工程理论与实践, 2014, 34(9): 2372-2379. [5] Tsyganok V V, Kadenko S V, Andriichuk O V. Significance of expert competence consideration in group decision making using AHP[J]. International Journal of Production Research, 2012, 50(17): 4785-4792. [6] Qi Xiaowen, Liang Changyong, Zhang Junling. Generalized cross-entropy based group decision making with unknown expert and attribute weights under interval-valued intuitionistic fuzzy environment[J]. Computers & Industrial Engineering, 2015, 79: 52-64. [7] Sen C G, Cinar G. Evaluation and pre-allocation of operators with multiple skills: A combined fuzzy AHP and max-min approach[J]. Expert Systems with Applications, 2010, 37(3): 2043-2053. [8] Amado C A F, Santos S P, Marques P M. Integrating the data envelopment analysis and the balanced scorecard approaches for enhanced performanceassessment[J]. Omega-International Journal of Management Science, 2012, 40(3): 390-403. [9] Govindan K, Kannan D, Shankar M. Evaluation of green manufacturing practices using a hybrid MCDM model combining DANP with PROMETHEE[J]. International Journal of Production Research, 2015, 53(21): 6344-6371. [10] 李珠瑞, 马溪骏, 彭张林. 基于离差最大化的组合评价方法研究[J]. 中国管理科学, 2013, 21(1): 174-179. [11] 陈国宏, 李美娟, 陈衍泰. 单一方法评价结论漂移性的测度研究[J]. 中国工程科学, 2004, 6(3): 58-63. [12] Goodman I R. Evaluation of combinations of conditioned information: A history[J]. Information Sciences, 1991, 57-58: 79-110. [13] Gregory A. The road to integration. Reflections on the development of organizational evaluation theory andpractice[J]. Omega, 1996, 24(3): 295-307. [14] Tsai W H, Lee P L, Shen Yushan, et al. A combined evaluation model for encouraging entrepreneurship policies[J]. Annals of Operations Research, 2014, 221(1): 449-468. [15] 郭亚军, 马赞福, 张发明. 组合评价方法的相对有效性分析及应用[J]. 中国管理科学, 2009, 17(2): 125-130. [16] 陈国宏, 陈衍泰, 李美娟. 组合评价系统综合研究[J]. 复旦学报(自然科学版), 2003, 42(5): 667-672. [17] 郭亚军, 易平涛. 一种基于整体差异的客观组合评价法[J]. 中国管理科学, 2006, 14(3): 60-64. [18] 陈衍泰, 陈国宏, 李美娟. 基于评价方法属性层次的组合评价研究[J]. 中国工程科学, 2005, 7(8): 56-59. [19] 张荣艳, 孙贵玲, 王爱苹. 组合评价模型在河南省主要城市综合经济实力评价中的应用[J]. 数学的实践与认识, 2013, 43(4): 60-67. [20] 陈衍泰. 基于方法集的组合评价研究[D]. 福州: 福州大学, 2004. [21] 李美娟, 陈国宏, 徐林明,等. 基于漂移度的动态组合评价方法研究[J]. 中国管理科学, 2015, 23(1): 141-145. [22] 柳玉鹏, 李一军. 组合评价方法在银行信用风险评价中的应用[J]. 中国管理科学, 2008, 16(S1): 215-218. [23] 毛定祥. 一种最小二乘意义下主客观评价一致的组合评价方法[J]. 中国管理科学, 2002, 10(5): 95-97. [24] 金菊良, 汪明武, 魏一鸣. 客观组合评价模型在水利工程方案选优中的应用[J]. 系统工程理论与实践, 2004,(12): 111-116. [25] 李惠林, 殷国富, 谢庆生等. 面向网络化制造的制造资源组合评价方法研究[J]. 计算机集成制造系统, 2008, 14(5): 955-961. [26] 李美娟, 陈国宏, 肖细凤. 基于一致性组合评价的区域技术创新能力评价与比较分析[J]. 中国管理科学, 2009, 17(2): 131-139. [27] 孙博文, 刘艳春. 基于模糊Borda组合评价法的电力行业上市公司经营绩效评价[J]. 数学的实践与认识, 2013, 43(10): 1-8. [28] 汪泽焱, 顾红芳, 益晓新,等. 一种基于熵的线性组合赋权法[J]. 系统工程理论与实践, 2003(3): 112-116. [29] 陈伟, 夏建华. 综合主、客观权重信息的最优组合赋权方法[J]. 数学的实践与认识, 2007, 37(1): 17-22. [30] 林元庆, 陈加良. 方法群评价中权重集化问题的研究[J]. 中国管理科学, 2002, 10(S1): 20-22. [31] 杭州商学院省自然科学基金课题组. “序号总和理论”及其在综合经济效益排序中的应用[J]. 数量经济技术经济研究, 1996,(1): 59-62. [32] 康楠, 郑循刚, 母培松. 基于组合评价的我国区域科技资源配置效率研究[J]. 华中科技大学学报(社会科学版), 2009, 23(6): 79-83. [33] 李美娟, 陈国宏, 陈勃,等. 基于方法集化的动态组合评价方法研究[J]. 中国管理科学, 2013, 21(2): 132-136. [34] 易平涛, 高立群, 郭亚军. 基于多源密度信息集结算子的组合评价方法[J]. 系统工程与电子技术, 2009, 31(12): 2882-2887. [35] 张立军, 陈跃, 袁能文. 基于信度分析的加权组合评价模型研究[J]. 管理评论, 2012, 24(5): 170-176. [36] 柳玉鹏, 李一军. 基于降维思想的客观组合评价模型[J]. 运筹与管理, 2009, 18(14): 38-43. [37] 王硕, 杨善林, 胡笑旋. 基于投影寻踪的组合评价方法研究[J]. 中国工程科学, 2008, 10(8): 60-64. [38] 陈国宏, 李美娟. 组合评价收敛性验证的计算机模拟实验[J]. 系统工程理论与实践, 2005(5): 74-82. [39] 李美娟, 陈国宏, 戴益军. 基于一致性组合评价的中国工业产业技术创新能力实证研究[J]. 中国科技论坛, 2009,(4): 51-56. [40] 彭张林, 张强, 李珠瑞,等. 改进的离差最大化决策模型及其在临近空间多任务规划中的应用[J]. 系统工程理论与实践, 2014, 34(2): 421-427. Research on a Recombination Evaluation Approach Based on the Previous Evaluation Results PENG Zhang-lin1,2, ZHANG Qiang1,2, WANG Su-feng3, YANG Shan-lin1,2 (1.School of Management,Hefei University of Technology,Hefei 230009,China;2.Key Laboratory of Process Optimization and Intelligent Decision-making,Ministry of Education,Hefei 230009,China;3.School of Management,Anhui Jianzhu University,Hefei 230601,China) The concept of combination evaluation is an important content in the comprehensive evaluation theory and methodology. In this paper firstly defines the term of recombination evaluation is firstly defined and a recombination evaluation approach is proposed based on the previous evaluation results, which mainly deal with the nonuniformity and poor convergence of the first evaluation results derived from different combination evaluation methods, such as fuzzy borda method, copeland method and maximizing deviation decision method. Then, some key processes and operation steps to conduct this approach are detailedly given, which includes description of comprehensive evaluation problem, description of single evaluation method, description of combination evaluation, consistency analysis of different evaluation results, selection of recombination evaluation method based on minimum drift and convergence analysis of the results of recombination evaluation. Finally, from the numerical examples, it can be seen that the result error of the recombination evaluation is far less than result from any single first combination evaluation. Therefore, the conclusion that the recombination evaluation has better combination results and is more effective can be drawn. The recombination evaluation approach can effectively improve uniformity and convergence of of the first evaluation results derived from different combination evaluation methods, and decrease error of the first combination evaluation results. Ultimately, the reliability of the overall evaluation results can be strengthened. The contribution of this paper includes: 1) firstly proposes and defines the term of recombination evaluation; 2) presents a selection rule of recombination evaluation method based on minimum drift and convergence analysis of the results of recombination evaluation; 3) constructs a methodology architecture to carry out this recombination evaluation approach. comprehensive evaluation; recombination evaluation; evaluation method; evaluation results 2015-07-29; 2016-01-22 国家自然科学基金重点项目(71131002);国家自然科学基金资助项目(71601066,71501055);教育部人文社会科学研究基金项目(16YJC6300093,15YJA790060) 简介:彭张林(1984-),男(汉族),安徽潜山人,合肥工业大学管理学院博士,研究方向:创新评价、优化决策,E-mail:pengzhanglin@163.com. C934 A 1003-207(2016)09-0156-09 10.16381/j.cnki.issn1003-207x.2016.09.019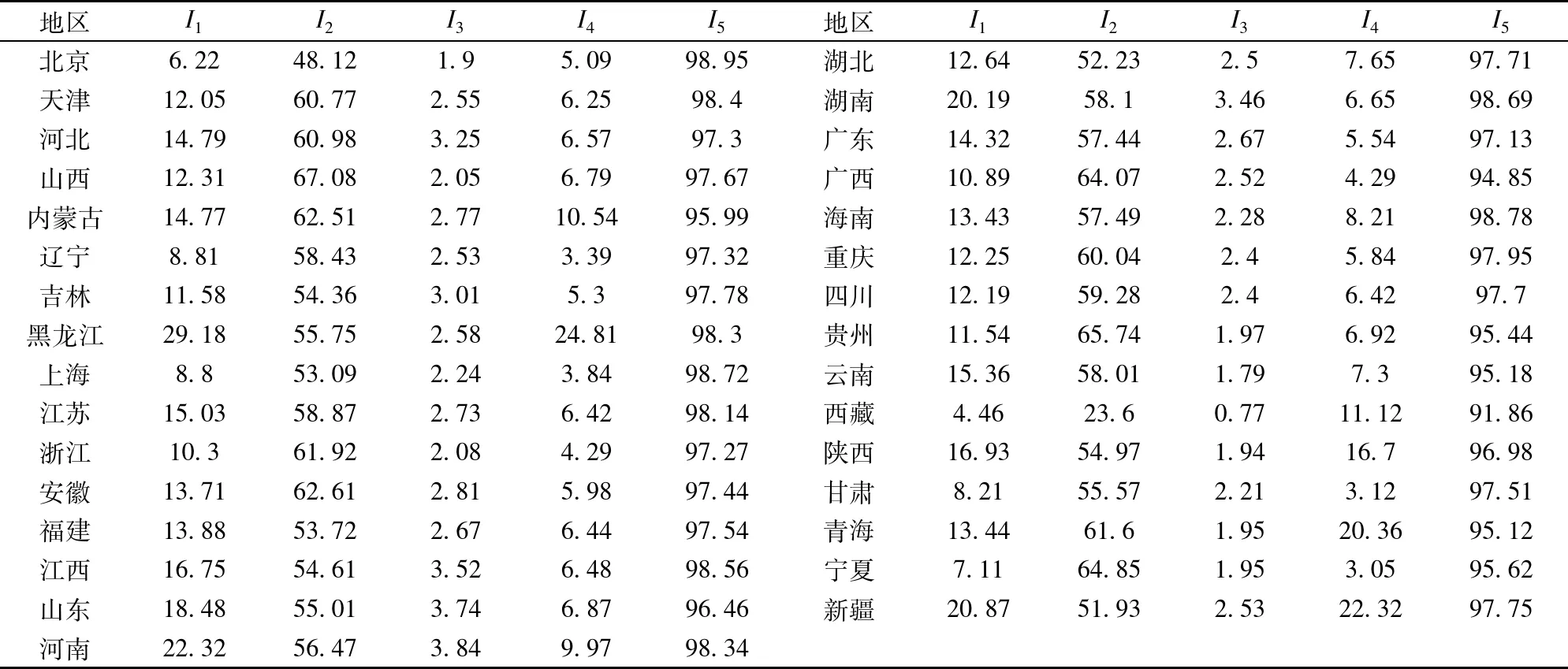
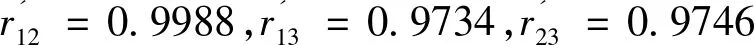
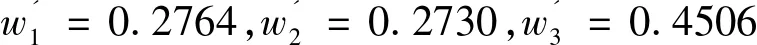
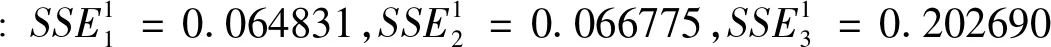
4 结语
